船撞设计冲击谱研究
2014-09-07王君杰喻志然
王君杰,喻志然
(同济大学 土木工程防灾国家重点实验室,上海 200092)
随我国内河及外海深水环境下桥梁建设日益增多,船舶碰撞桥梁事故频繁发生。桥梁被撞不仅会致大桥结构损伤,且桥梁使用寿命、安全性及抗震性能均会受到损失[1]。
1 船撞设计冲击谱的提出
船舶撞击桥梁研究内容主要有船舶撞击桥梁概率、撞击动能、对桥墩或防撞系统撞击力及桥梁船撞需求分析等。桥梁船撞需求分析主要研究求解桥梁在船撞力作用下反应。桥梁船撞需求分析方法主要有等效静力法、碰撞有限元数值模拟方法及简化动力分析方法等。等效静力法给出不同船舶在不同速度下撞击力计算公式,将撞击力以静力形式施加于桥梁结构求解其反应。规范[2-4]所用等效静力方法忽略船桥碰撞问题的动力本质,而有限元数值模拟方法可较精细模拟船桥碰撞中各种动力因素,但对使用者要求较高,未得到工程设计的广泛采用。简化动力分析方法介于该两方法之间,在保持计算效率基础上可弥补静力法局限,但仍存较多关键问题尚未解决。
对大多船撞事故,桥梁结构仅局部损伤,整体结构仍处于弹性范围。在结构抗震研究中,通过求解不同自振周期的单自由度体系在地震动时程作用下反应给出其反应谱,并通过多条地震动时程反应谱统计给出设计谱。地震反应谱分析利用设计谱求得结构各阶振型峰值反应,并通过各阶振型峰值反应组合获得结构总峰值反应。而如何通过船撞冲击谱确定桥梁船撞需求实为有意义的研究[5-6]。
2 冲击荷载作用下单自由度体系响应求解
卜令涛[7]建立9种代表性船舶有限元模型,通过计算各种船舶在9种不同速度下撞击刚性墙,获得81条撞击力时程曲线。部分船舶船艏有限元模型见图1,部分时程曲线见图2。
本文以图2撞击力时程为荷载,通过编程实现激励插值法[8],求解周期及阻尼比变化的单自由度体系反应,部分结果见图3,横轴以10为底对数坐标系周期T,纵轴为单自由度体系位移反应的放大系数,ξ为阻尼比。位移放大系数定义为

图1 代表性船舶船艏有限元图
(1)
式中:um为体系在冲击荷载时程作用下位移反应最大值;ust为体系在冲击荷载时程峰值Pm作用下静力位移反应。
由计算结果知,① 在相同荷载时程作用下,不同周期体系位移放大系数差别较大;在不同荷载时程作用下,相同周期体系位移放大系数差别亦较大;主要原因为荷载时程频谱特性的随机性对体系反应影响较大;② 当自振周期较长时,体系位移放大系数按一定规律衰减;原因为持续时间较短的冲击荷载时程对体系作用仅相当于一个冲量作用,荷载时程频谱特性对体系反应影响减小。
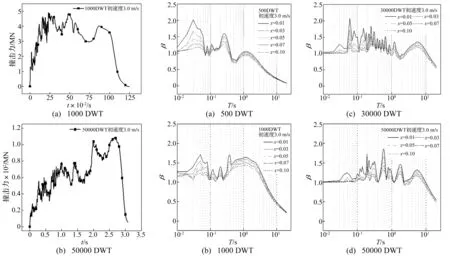
图2 船舶撞击力时程曲线举例
体系反应用放大系数衡量可避免荷载时程峰值对反应的影响;荷载持时对短周期体系线性反应影响不大,对长周期体系影响较大;荷载时程频谱特性对不同周期体系均有影响。基于此,考虑用统计方法获得冲击谱,具体统计过程见下节。将所有荷载时程作用计算结果绘于同一坐标系下,并求每个周期断面反应均值,见图4。
据计算结果设统计位移放大系数曲线见图5,横轴为以10为底的对数坐标系。自振周期为0即体系为绝对刚体时,体系动力响应、静力响应相等,即放大系数为1;自振周期0
3 船撞冲击谱统计
位移放大系数曲线第一特征点(T1,β1)中β1期由图4中各断面放大系数均值最大值决定,计算结果发现在不同阻尼比ξ下,β1均在体系T=0.08s时取最大均值,即T1=0.08 s,β1取值与阻尼比有关,当ξ=0.05时,β1=1.258 8。位移放大系数曲线第二特征点(T2,β2)由每个时程荷载所得具体体系反应决定。当ξ=0.05时,拟合T2与船舶吨位DWT及船速V的关系见图6。由图6看出拟合总体结果较好,拟合关系式为
T2=0.1666DWT0.283V0.2942
(2)

图4 计算结果统计图
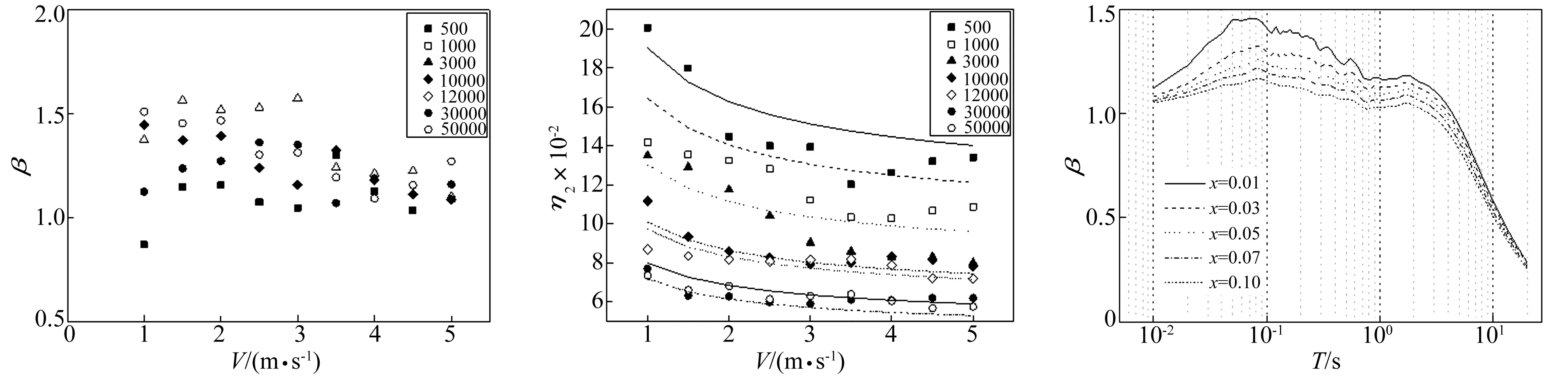
图7 β2与船吨位DWT、船速V关系图
β2与船舶吨位DWT、船速V关系见图7。由图7看出,β2分布随机性较强,与船舶吨位DWT及船速V无明显关系,故取其均值β2=1.1282。位移放大系数曲线第三段,β随T的增大按指数衰减,ξ=0.05时拟合衰减系数η2与船舶吨位DWT及船速V关系见图8。由图8看出拟合效果较好,拟合关系式为
η2=0.7028DWT-0.2111(0.4208V-0.6091+0.5833) (3)
由图9看出,阻尼比ξ对放大系数β均值影响不可忽略。以上位移放大系数曲线特征统计均在阻尼比ξ=0.05下进行,考虑阻尼对体系反应影响,设各周期体系阻尼比对放大系数影响与第一特征点(T1,β1)阻尼比ξ对放大系数β影响相同。以ξ=0.05时阻尼影响系数η1=1为目标拟合η1与阻尼比ξ关系为
η1=2.363-1.71ξ0.07588
(4)
综上所述,给出图5的位移放大系数谱数学表达式为
(5)
式中:特征点T1=0.08 s;β1=1.258 8;T2按式(2)求β2=1.128 2;k1=(η1β1-1)/T1,k2=η1(β2-β1)/(T2-T1)为设计位移放大系数谱斜率;阻尼比影响系数η1按式(4)求得,第三段衰减率η2按式(3)求得。
部分设计位移放大系数谱与实际位移放大系数谱见图10,阻尼比均为0.05。由图10看出,设计谱与实际谱增长衰减趋势相同,由于设计谱由较多实际谱统计所得,因此具有统计规律。

图10 设计位移放大系数谱与实际位移放大系数谱比较
位移放大系数为体系动力反应最大值与体系在实际冲击荷载峰值作用下静力反应比值,在利用冲击谱求体系动力反应前,需先求得体系在冲击荷载峰值作用下的静力反应。荷载时程峰值Pm(MN)与DWT(t)及V(m/s)之关系[7]为
Pm=0.07721DWT0.57V
(6)
由位移放大系数谱及荷载时程峰值给出冲击谱数学表达式为
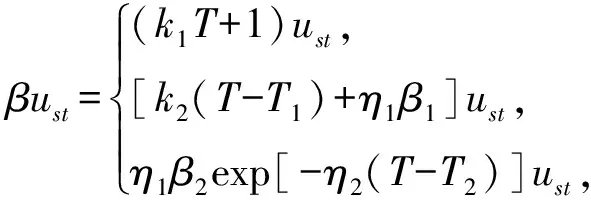
(7)
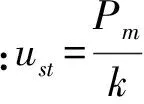
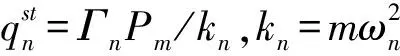
在冲击荷载作用下,求得结构各阶模态反应最大值后需用合适的组合方法获得结构总反应峰值。文献[5]提出利用地震中所用CQC或SRSS方法组合结构各阶模态反应最大值获得结构总反应的最大值。文献[6]在上两种方法基础上增加结构各阶模态反应最大值绝对值相加的ABSSUM方法。文献[9]提出用SRSS、ABSSUM及NRL方法进行组合,其中NRL方法为将各阶模态反应最大值中最大一阶提出来,将剩余模态反应最大值进行SRSS组合后再与上述提取值求和;但该组合方法精度尚需大量实际工程计算检验。
4 结 论
本文利用有限元模拟不同吨位船舶在不同速度下撞击刚性墙获得撞击力时程,计算不同周期、不同阻尼比单自由度体系在撞击力时程作用下位移峰值,并用此位移峰值除以撞击力峰值作用下静力位移,获得位移放大系数。通过寻找位移放大系数统计规律,给出有统计意义的船撞冲击谱及其具体使用步骤。
[1] 刘建成,顾永宁.船-桥碰撞力学问题研究现状及非线性有限元仿真[J].船舶工程,2002(5):4-9.
LIU Jian-cheng,GU Yong-ning.A review of approaches to mechanism of ship-bridge collision and its nonlinear FEM simulation[J].Ship Engineering,2002(5):4-9.
[2] AASHTO.Guide specification and commentary for vessel collision design of highway bridges[M].Washington: American Association of State Highway and Transportation Officials,2009.
[3] Vrouwenvelder A C W M.Design for ship impact according to eurocode 1,part 2.7[M].Ship Collision Analysis, 1998.
[4] JTJ D60-2004,公路桥涵设计通用规范[S].
[5] Cowan D R.Development of time-history and response spectrum analysis procedures for determining bridge response to barge impact loading[D].University of Florida, 2007.
[6] 江震.船撞动力需求时程及冲击谱分析方法[D].上海:同济大学,2013.
[7] 卜令涛.船舶对桥梁冲击作用的简化概率方法[D].上海:同济大学,2011.
[8] Chopra A K.Dynamics of structures(2ndedition)[M].北京:清华大学出版社,2005.
[9] 汪玉,华宏星.舰船现代冲击理论及应用[M].北京:科学出版社,2005.
[10] 梁利华,荀盼盼,王保华.基于ARMA模型的水下爆炸冲击谱预测[J].振动与冲击,2013,32(13):23-26.
LIANG Li-hua,XUN Pan-pan,WANG Bao-hua.Shock response spectrum prediction of underwater explosion based on an ARMA model[J].Journal of Vibration and Shock,2013,32(13):23-26.
