栓接结合部动态特性参数辨识新方法
2014-09-07蔡安江蔡力钢阮晓光郭铁能
李 玲,蔡安江,蔡力钢,阮晓光,郭铁能
(1.西安建筑科技大学 机电工程学院,西安 710055;2.北京工业大学 机械工程与应用电子技术学院,北京 100124)
由于机床中存在大量结合部,使结构连续性被破坏,从而表现出复杂的动力学特性,极大程度影响整机动态性能。研究表明,机床中结合部的接触刚度约占机床总刚度的60%~80%,接触阻尼占机床全部阻尼的90%以上[1];因此,开展结合部动静力学特性研究成为机械系统由单件分析走向整机分析的关键,亦为整机性能预测的基础。

上述方法主要辨识栓接结合部等效刚度参数,未对等效阻尼参数进行辨识。为能准确反映栓接结合部动态特性,针对采用频响函数进行结合部参数辨识出现的不适定问题,本文提出新的辨识方法。与文献[16]及实验结果比较表明,采用本文方法可避免利用频响函数法辨识结合部参数时出现的不适定问题,能达到准确辨识栓接结合部等效参数目的。
1 栓接结合部模型
忽略栓接结合部质量,并设两子结构间栓接结合部可通过一组线性弹簧及阻尼器表示,见图1,整体结构由子结构A,子结构B及栓接结合部三部分组成,其中c1,…,cm表示结构栓接结合部区域,共m个节点;a区、b区分别表示子结构A,B除栓接结合部外区域;knm,ktm,dnm,dtm分别表示栓接结合部法向、切向接触刚度与接触阻尼。据动力学方程将子结构A,B分别表示为
(1)
(2)
式中:M,D,K分别为质量阵、阻尼阵、刚度阵;x,f分别为结构位移向量、受力向量;下标j为栓接结合部区域。
设无外界力、力矩作用于栓接结合部,且式(1)、(2)均满足力平衡及位移相容性条件,则
Afj=-Bfj=fj,Afa=Bfb=0,Axc-Bxc=0
(3)
Dj=diag(d1,d2,…,dm),Kj=diag(k1,k2,…,km)。

图1 整体结构分解为两子结构与栓接结合部
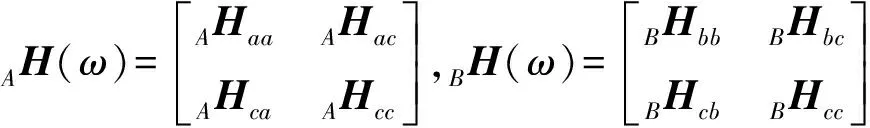
(4)
据式(1)~式(4)得整体结构频响函数[18]:
(5)
式中:α′=α-1,α=(AHcc+BHcc+Pj);

栓接结合部法向、切向等效刚度与等效阻尼参数可据式(5)辨识获取。获取频响函数时需注意激振力、加速度信号分别在各结构法向、切向激振与拾取。
通过实验验证,忽略栓接结合部法向与切向耦合效应,对整体结构响应影响不大[16];因此,栓接结合部等效刚度与等效阻尼模型可表示为
(6)
式中:Kjn,Djn,Kjn,Djn分别为栓接结合部法向与切向等效刚度及等效阻尼。
2 参数辨识
据文献[18]将式(5)中任意一组等式表示为通式
Hγ=Hυα′Hβ
(7)
通过实验或有限元方法可获得整体结构与两子结构的频响函数,利用奇异值分解法辨识出栓接结合部等效参数为
Y=Pj[Hβ-(AHcc+BHcc)Y]
(8)

(9)
式中:l为对辨识结果取值个数;kj,dj为栓接结合部等效刚度与等效阻尼平均值。
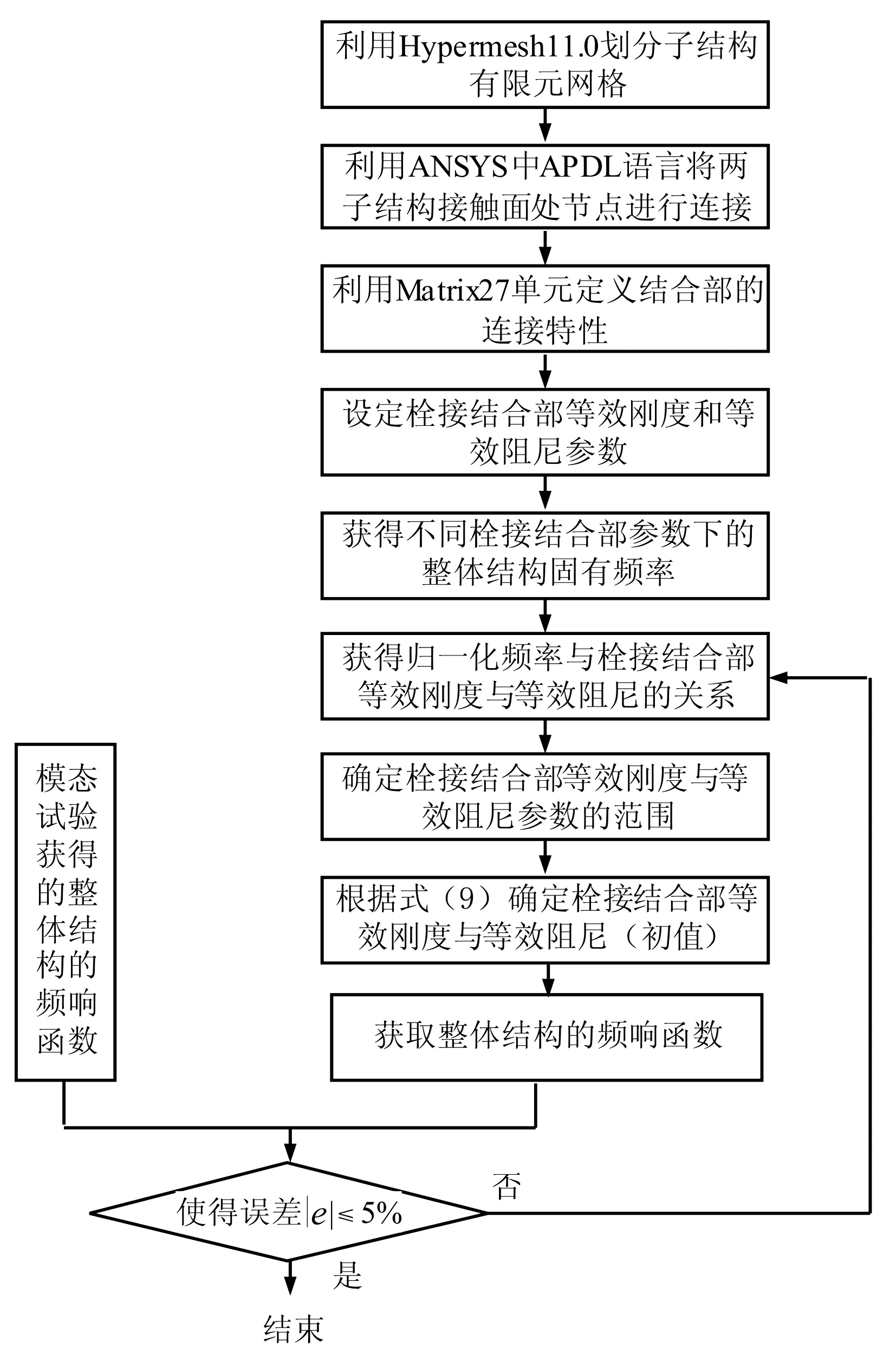
图2 参数辨识流程图
理论上,通过式(8)可准确辨识出栓接结合部的等效参数Pj;然而,由于实验时测量数据、噪声干扰及数值运算(矩阵求逆)等所致误差,使辨识结果出现不适定问题;因此,在参数辨识时需作处理,即利用有限元模型修正方法对任意子结构进行模态分析,将其结果与模态实验数据比较,确定结构弹性模量E、泊松比υ及密度ρ;利用Hypermesh11.0及ANSYS12.0有限元分析软件分别进行网格划分、接触面处节点连接、定义、赋值;获得归一化频率与不同栓接结合部参数间关系,确定栓接结合部等效刚度与等效阻尼参数区间;利用式(9)获得等效刚度与等效阻尼的平均值为初始值,以实验与仿真整体结构频响函数误差最小为目标,用迭代法求栓接结合部等效刚度、等效阻尼参数。整个辨识流程见图2。
利用上述方法可避免辨识时因不适定性导致的问题,提高辨识精度。
3 实验研究
3.1 有限元模型修正
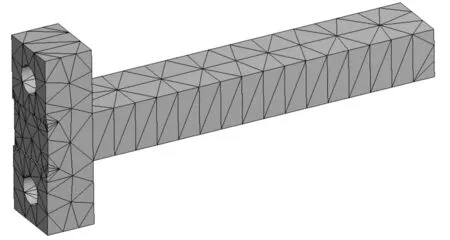
图3 试件有限元模型
设计子结构A,B结构相同,两结构间用高强度螺栓连接。以子结构A为例将试件划分为800个单元,1 636个节点,见图3。为验证辨识结果的正确性,需确定子结构A实验频响函数与有限元仿真频响函数一致;因此,利用有限元模型修正法将实验所得频响函数与修正后模型频响函数比较,确定子结构A的尺寸及材料特性,见表1。修正后频响函数与实验所得频响函数比较见图4。

表1 基本结构尺寸及材料特性
3.2 实验研究
据模态实验测试原理,搭建整体结构模态测试实验系统,见图5。将试件通过两高强度螺栓连结,螺栓规格M16,长90 mm,10.9 S级。高强度螺栓中内置应变片,通过动态应变仪可测量螺栓预紧力大小。为模拟自由状态,将试件两端用细尼龙绳悬挂。以锤击为激振方式,以加速度传感器在所选位置上获取的信号为加速度频响函数数据。为减少加速度传感器重量对结构动态特性影响,用较小加速度传感器(PCB系列)。试验前需选合适的激发及窗函数。应本实验研究对象为梁结构,为避免扭转模态影响,加速度传感器置于梁中心线上,使振动为单纯一维梁振动。所选频率范围0~1 500 Hz,采样频率2 Hz。试件表面粗糙度3.2 μm,取预紧力30 kN。
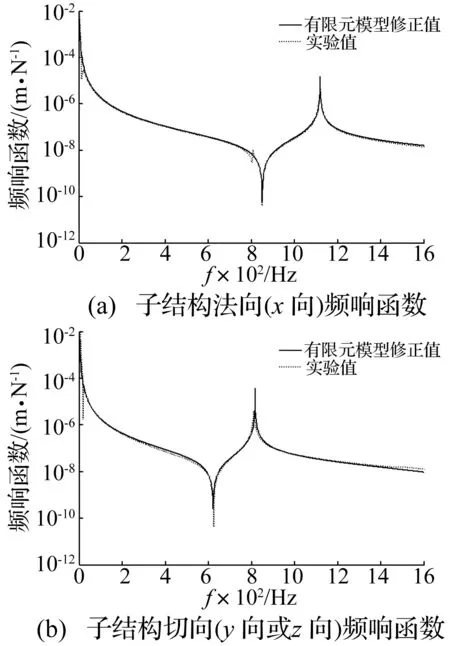
图4 实验与有限元模型修正模型频响函数比较

图5 实验原理
整体结构法向、切向激振与拾取方式见图6。其中图6(a)为法向激振与加速度频响函数的拾取实验,图6(b)为切向激振与加速度频响函数的拾取实验。拾取与激振位置须在同一方向,激振点在加速度传感器附近。

图6 实验激振与拾取方式
3.3 栓接结合部参数辨识
用Hypermesh11.0软件实现接触面处均布755个节点,用ANSYS12.0中APDL语言自编的自动化程序连接接触面上各节点,用Matrix27单元定义栓接结合部等效刚度、等效阻尼参数,建立整体有限元模型见图7。通过该模型设置不同的栓接结合部等效刚度、等效阻尼参数,可得整体结构各阶固有频率及模态振型。
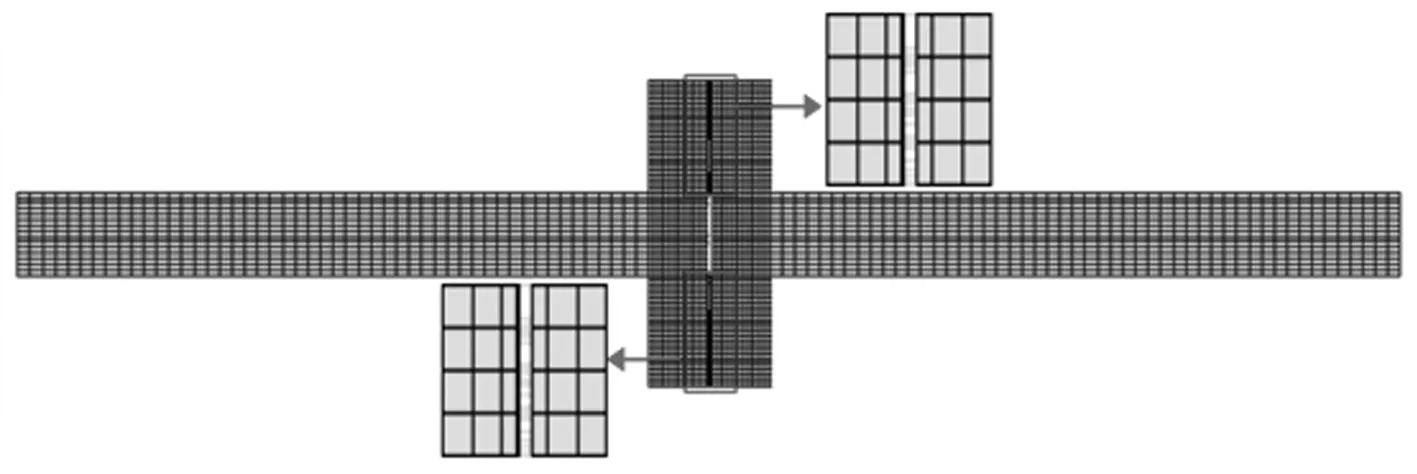
图7 整体有限元模型
通过对栓接结合部等效参数与整体结构第一阶固有频率灵敏度分析,得归一化频率与栓接结合部接触刚度、接触阻尼关系,见图8~图11。由图8、图9可知,栓接结合部法向等效刚度辨识结果处于108~1011N/m之间,法向等效阻尼辨识结果处于105~5×106N·s/m之间。由图10、图11可知,栓接结合部切向等效刚度辨识结果处于107~108N/m之间,切向等效阻尼辨识结果处于20 ~60 N·s/m之间。

图8 法向刚度与归一化固有频率关系
据式(9)分别对栓接结合部接触刚度、接触阻尼取值范围的平均为初值,以实验与仿真整体结构频响函数误差最小为目标,通过迭代方法确定栓接结合部等效刚度与等效阻尼值,结果见表2。

表2 栓接结合部辨识等效参数值

图11 切向阻尼与归一化固有频率关系
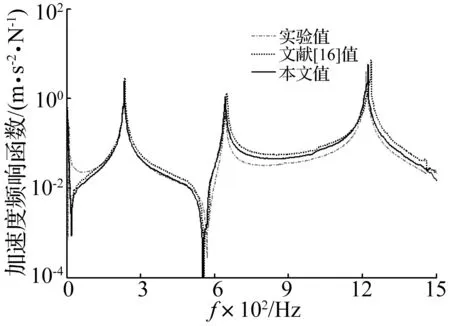
图12 整体结构频响函数比较
将辨识结果与文献[16]数据比较知,最大误差发生在切向接触阻尼处为8.96%,最小误差仅3.14%,发生在法向接触刚度处,由此表明辨识结果的正确性。据式(6)将辨识结果代入ANSYS12.0中Matrix27单元,利用谐响应法求解整体结构频响函数,并将仿真结果与文献[16]及实验结果比较,见图12。由图12看出,本文所得结果与文献[16]结果及实验结果非常接近,亦表明本文方式的正确性。
4 结 论
针对采用频响函数辨识栓接结合部等效参数时出现的不适定问题,提出新辨识方法并获取正确的等效参数,结论如下:
(1) 通过对栓接结合部等效参数与整体结构第一阶固有频率灵敏度分析,确定栓接结合部等效刚度与等效阻尼的取值范围,取该范围值平均值为初值,以实验与仿真整体结构的频响函数误差最小为目标,通过迭代方法确定栓接结合部等效刚度与等效阻尼值。
(2) 利用ANSYS12.0有限元软件中Matrix27单元模拟栓接结合部等效特性,忽略法向与切向耦合效应求解整体结构结果表明,栓接结合部法向与切向相互耦合效应对整体特性影响较小,实际工程中可忽略。
(3) 通过实验研究及与文献[16]比较结果表明,最大误差发生在切向接触阻尼处,最小误差发生在法向接触刚度处。采用本文方法与实验结果更接近。
[1] 蔡力钢,李玲,郭铁能,等.基于不完备频响函数辨识结合部参数的研究[J].振动工程学报, 2011,24(4):345-350.
CAI Li-gang,LI Ling,GUO Tie-neng,et al.Identifying mechanical joint dynamic parameters based on incomplete frequency response functions[J].Journal of Vibration Engineering,2011,4(4):345-350.
[2] Mao Kuan-ming,Li Bin,Wu Jun,et al.Stiffness influential factors-based dynamic modeling and its parameter identification method of fixed joints in machine tools[J].International Journal of Machine Tools & Manufacture,2010,50(2):156-164.
[3] Xue Yue.Developments of joint elements and solution algorithms for dynamic analysis of jointed structures[D].Ph.D thesis,University of Colorado,2002.
[4] 屈重年,伍良生,马建峰,等.铁基多孔含油固定结合面法向动态特性研究[J].振动与冲击,2013,32(13):56-61.
QU Chong-nian,WU Liang-sheng,MA Jian-feng,et al.Normal dynamic characteristics of a fixed joint interface with oily Fe-based porous-media[J].Journal of Vibration and Shock,2013,32(13):56-61.
[5] Mottershead J E,Stanway R.Identification of structural vibration parameters by using a frequency domain filter[J].Journal of Sound and Vibration,1986,109:495-506.
[6] Tsai J S,Chou Y F.The identification of dynamic characteristics of a single bolt joint[J].Journal of Sound and Vibration,1988,125:487-502.
[7] Wang J H,Liou C M.Experimental Identification of Mechanical Joint Parameters[J].Journal of Vibration and Acoustics,1991,113(1):28-36.
[8] Wang J H,Chuang S C.Reducing errors in the identification of structural joint parameters using error functions[J].Journal of Sound and Vibration,2004,185(5):295-316.
[9] Ren Y,Beards C F.Identification of joint properties of a structure using FRF data[J].Journal of Sound and Vibration,1995,186(4):567-587.
[10] Ren Y,Beards C F.Identification of “effective” linear joints using coupling and joint identification techniques[J].American Society of Mechanical Engineers Journal of Vibration and Acoustics,1998,120(2):331-338.
[11] Liu W,Ewins D J.Substructure synthesis via elastic media[J].Journal of Sound and Vibration,2002,257(2):361-379.
[12] Yang T,Fan H S,Lin S C.Joint stiffness identification using FRF measurements[J].Computers and Structures, 2003, 81(28/29): 2549-2556.
[14] 郭铁能,李玲,蔡力钢,等.基于频响函数辨识机械结合部动态参数的研究[J].振动与冲击,2011,30(5):69-72.
GUO Tie-neng,LI Ling,CAI li-gang,et al.Identifying mechanical joint dynamic parameters based on measured frequency response functions[J].Journal of Vibration and Shock,2011,30(5):69-72.
[15] 李玲,蔡力钢,蔡安江,等.不同预紧力下栓接结合部切向等效特性研究[J].振动、测试与诊断,2013,33(1):82-87.
LI Ling,CAI Li-gang,CAI An-jiang,et al.Tangential equivalent properties of the bolted joints in different preload[J].Journal of Vibration,Measurement and Diagnosis,2013,33(1):82-87.
[16] Guo Tie-neng,Li Ling,Cai Li-gang,et al.Alternative method for identification of the dynamic properties of bolted joints[J].Journal of Mechanical Science and Technology,2012,26(10): 3017-3027.
[17] 李玲,蔡力钢,郭铁能,等.机械结合部动态刚度辨识与实验研究[J].振动工程学报,2012,25(5):488-496.
LI Ling,CAI Li-gang,GUO Tie-neng,et al.Identification and experimental research on dynamic stiffness of mechanical joints[J].Journal of Vibration Engineering,2012,25(5): 488-496.
[18] 李玲,蔡安江,蔡力钢,等.栓接结合部动态特性辨识方法[J].机械工程学报,2013,49(7):168-175.
LI Ling,CAI An-jiang,CAI Li-gang,et al.Identification method for dynamic properties of bolted joints[J].Journal of Mechanical Engineering,2013,49(7):168-175.
