基于振型转换的螺栓连接梁非线性振动研究
2014-09-07卫洪涛孔宪仁王本利张相盟
卫洪涛,孔宪仁,王本利,张相盟
(1.郑州大学 力学与工程科学学院,郑州 450001;2.哈尔滨工业大学 卫星技术研究所,哈尔滨 150086)
连续体的非线性振动在航天器结构中是广泛存在的现象,如采用销接连接以及套筒连接的桁架结构[1-2]、带有展开机构的天线、太阳帆板,以及火箭发射时载荷的特定模态[3],可以简化为带有非线性边界条件的连续体振动系统,其边界条件如迟滞效应[4],连接结构中的摩擦力[5]、间隙[6]等是较常见的非线性特性,研究人员认为,航天器的连接结构非线性对整体结构振动响应的影响是显著的[7],典型的如航天器结构地面振动实验中的基频漂移现象[3],对发射安全具有潜在的危害,对航天器结构非线性振动的研究一直以来都得到了航天领域工程师们的重点关注。
前人对于螺栓连接结构的研究包括实验研究[8-10]及建模研究[11-14],螺栓连接结构的静力实验结果表现出典型的迟滞非线性特性[9],对其力学特性进行建模的模型包括Iwan模型[11],Masing模型[12],Praiseich模型[14]等,有研究证明其本质是一样的,可以统一用Iwan模型来表示[12]。近年来,螺栓连接对连续体的振动影响多集中在实验研究上,针对不同的对象,如两段用螺栓连接的梁[9],带螺栓连接的框架等[8],研究人员得到了连接的力学特性以及其对简单结构的动力学响应影响,但是从文献报导看,螺栓连接对结构振动的影响并没有得到彻底的理论研究。
带有螺栓连接的结构振动,可以看作带有时变非线性边界条件的连续体振动问题,此类问题包括边界带间隙连接结构的结构振动问题,前人在解决边界带间隙的连接结构系统上,采取基于振型转换思想的数值方法,如Moon等[15]采取单振型近似,利用梁上特殊点将系统方程连续化,揭示了系统在特定参数下的混沌振动;Shaw[16]利用单振型研究了单侧阻挡弹簧的悬臂梁的非线性动力学问题,认为单振型近似足够用于进行定性研究,得到了与实验结果近似的结论;Chuang[17]研究了一端夹支,一端具有带间隙的单弹簧阻挡的梁的非线性振动,总结并评价了前人研究类似问题的两种方法,即力积分法和振型转换法,并分别用这两种方法对带单阻挡的悬臂梁算例进行了数值研究,讨论了阻挡弹簧的刚度对梁幅频响应的影响,认为振型转换法比力积分法有更广的适用范围。基于振型转换的思想,Ervin[18-19]研究了一个两端夹支中间带刚体的梁的撞击问题,得到了如分岔、亚谐波共振、超谐波共振、混沌等非线性动力学现象;Shih等[20]取微坐标测量器为背景,考虑了振型耦合的影响;另外一些基于振型转换的连续体撞振问题研究见文献[21-22],对于边界条件是Iwan模型建模的迟滞非线性系统,文献[17]中的步骤已不适用,新的普适的方法有待建立。
基于振型叠加及传递的思想,结合Iwan模型,本文利用前面工作中提出的一种可以求解分段线性边界条件连续体振动问题的新方法——相对振型转换法[23]来求解带有螺栓非线性边界条件连续体振动问题。这是首次基于振型转换的思想尝试求解此类振动问题,研究了其代表的一类非线性系统受迫振动时的响应。
1 研究方法描述
1.1 基于时间驱动的Iwan模型
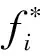
(1)
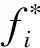
(2)
式中φ(f*)取决于实验数据,可有不同的形式[24],下文的研究中采用经典的均布函数,引入参数 Δf为分布宽度,β=Δf/(2fy),有屈服力分布函数表达式:
H[f*-fy(1+β)]}
(3)
其中H( )为Heaviside函数。

图1 Iwan模型结构图
为了简化建模仿真,重新构造Jenkin’s单元的力-位移关系式,得到基于时间驱动的Iwan模型,与经典的基于位移的表达式相比,该表达式在加载阶段及饱和输出阶段具有统一的形式。有:
fJ=
(4)
其中a(tn)为tn时刻Jenkin’s单元的输入位移。
1.2 一端固支一端螺栓连接梁相对振型转换法

图2 端点带螺栓连接梁结构示意图
对于一端固支一端带螺栓连接结构的对象如图2所示,利用Iwan模型对其右端的连接结构进行建模,由1.1节知,在梁的一个振动周期内,每当有Jenkin’s单元屈服时,Iwan模型的刚度会减小,其边界刚度会经历减小-增大-减小的循环过程,具体力-位移关系见图3,因此该系统的振动本质上可看作为分段线性边界条件问题,可用相对振型转换法对其进行处理。
梁的振动方程可以表达为:
(5)
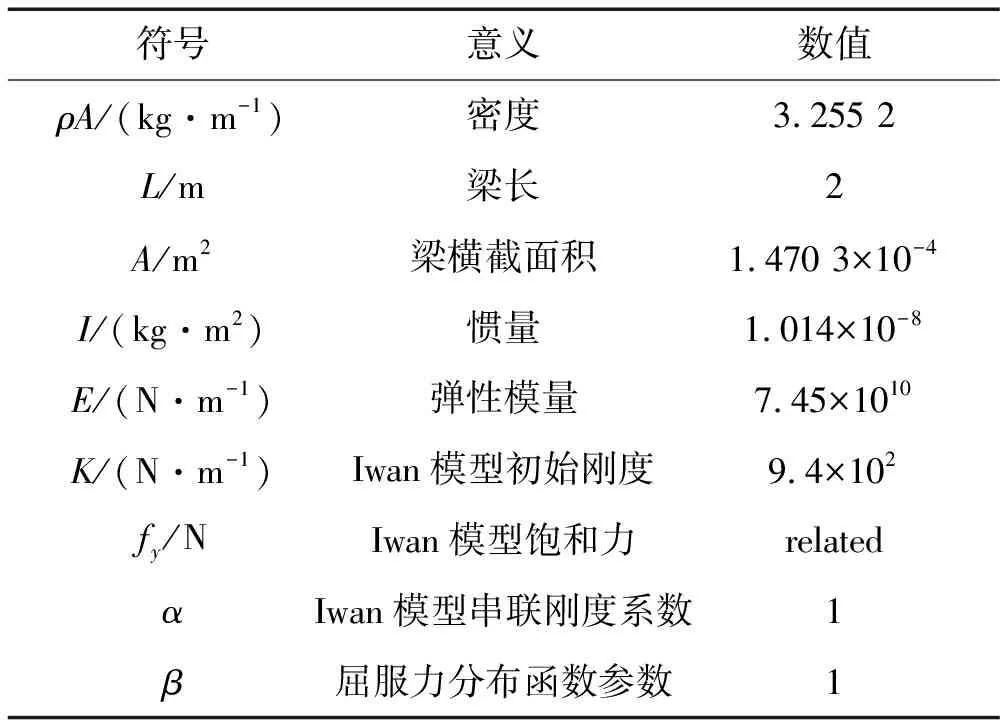
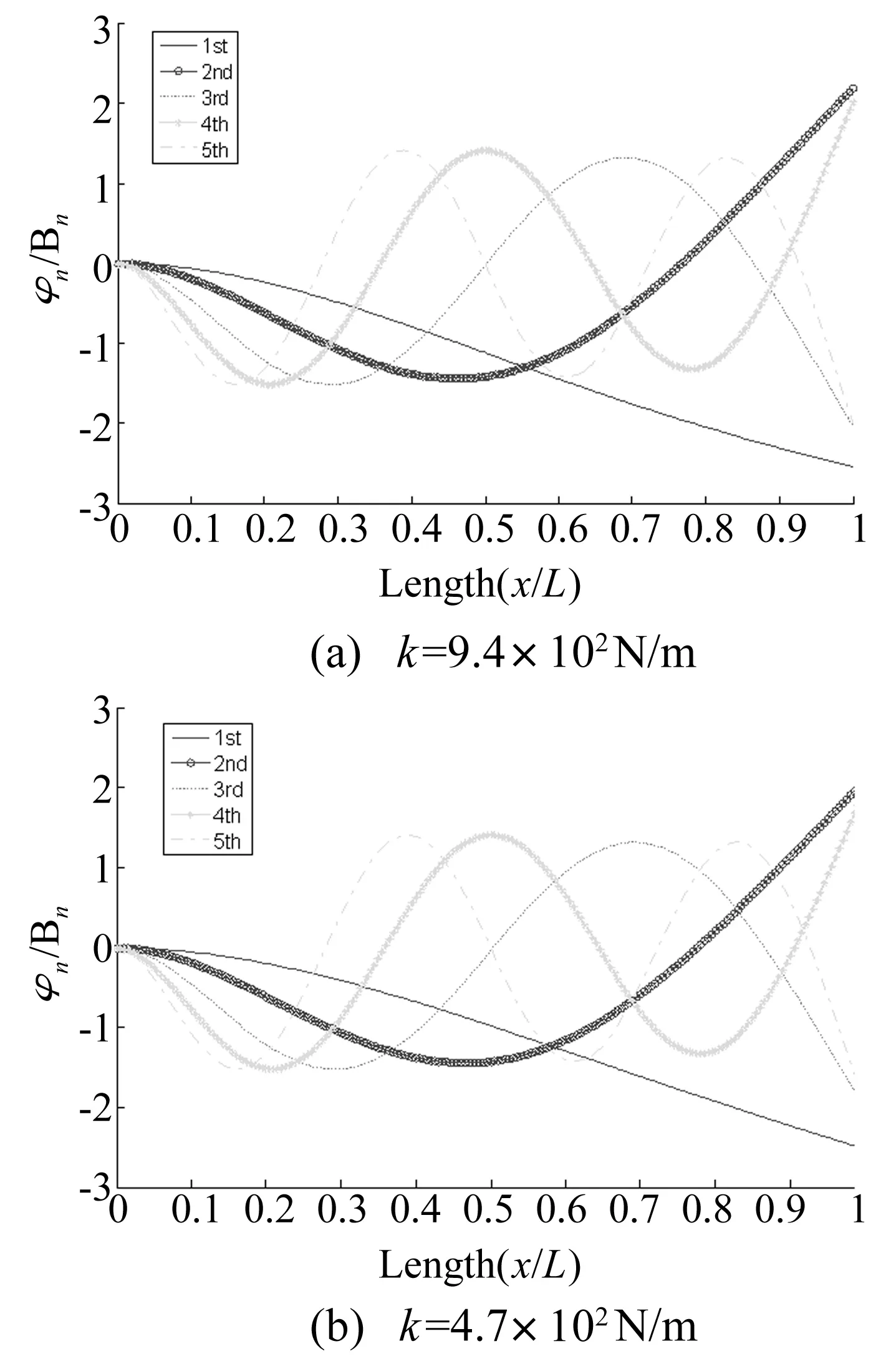
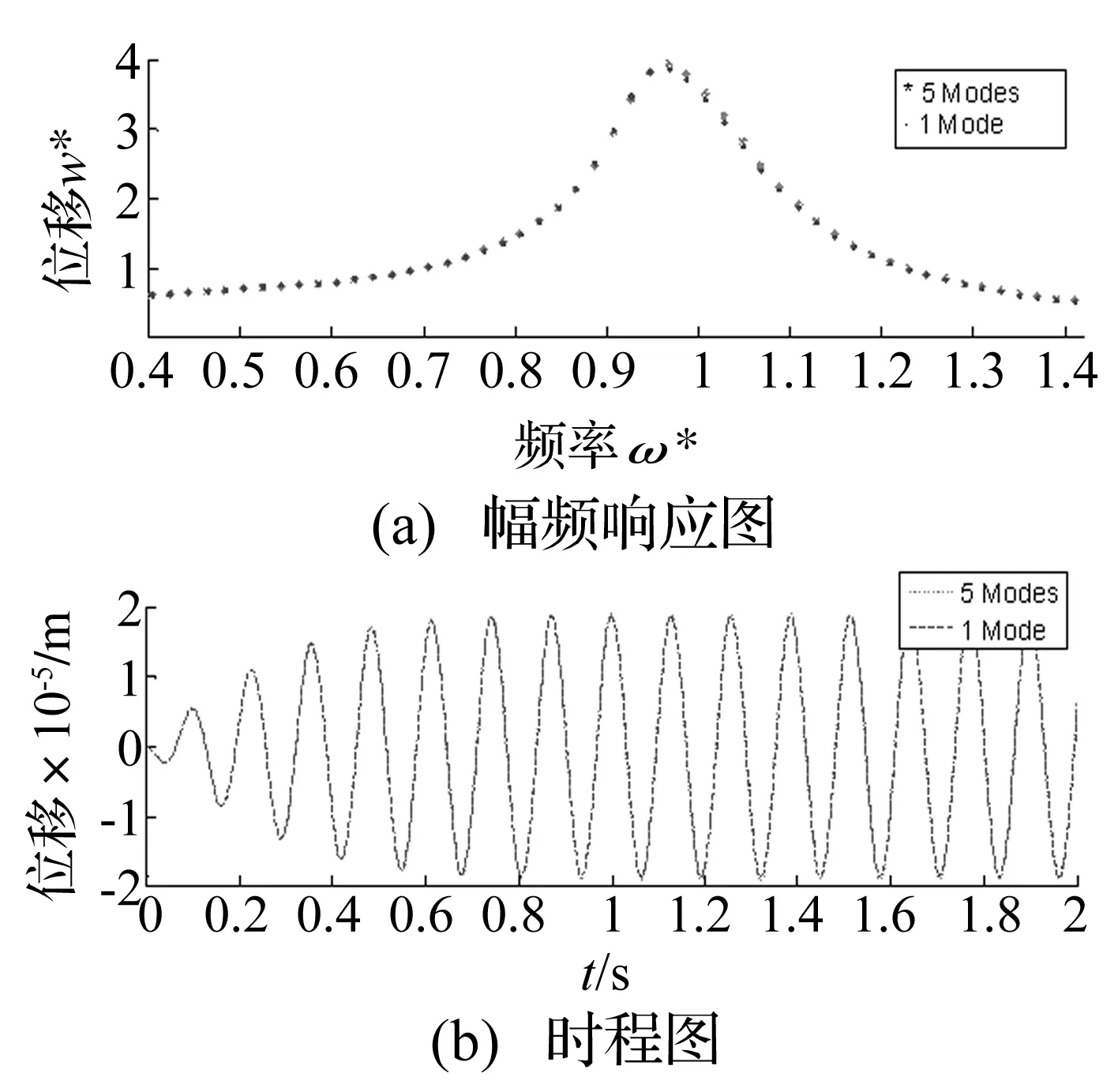
式中,δ(x-L)为狄拉克函数,F(x,t)=f(x)cos(ωt)为激励力,V(t)为螺栓连接对梁的横向反力,令梁从静止开始受激励力作用,采用包含N个Jenkin’s单元的Iwan模型对螺栓连接进行建模,假设t1时刻第一个Jenkin’s单元屈服,t1时刻前系统为线性振动,梁上任一点的横向位移可以表达为w(x,t)=w1(x,t),t2时刻Iwan模型的第二个Jenkin’s单元屈服,t1~t2时刻系统同样处于线性振动状态,t1时刻发生一次振型转换,系统由刚度为k的振型转换为刚度为k(N-1)/N振型,令梁的振型为边界条件转换前的振型叠加上转换后的振型,则梁上任一点的横向位移为:w(x,t)=w1(x,t1)+w2(x,t),以此类推,假设某ti时刻,系统经历第M(M (6) 取前S阶振型来近似: (7) 式中φin(x),φrn(x)为对应边界条件梁振型,ain(t),arn(tr)为振型振幅,有边界螺栓连接的反力V(t)=-Kw(L,t),将式(6)代入到梁的振动方程(5)中,利用Galerkin方法进行处理,可以得到任意t时刻系统的振动方程: j=1…S (8) 式中tr为边界条件发生改变的时刻点。 Fj= (9) (10) 有: (11) 考虑算例参数如表1。 表1 系统参数表 如前文所述,参数辨识不是本文的研究目的,所以在利用Iwan模型对螺栓连接建模时,取Jenkin’s单元个数N=2,5,20,其余参数如表1,则Iwan模型的力-位移曲线图如图3所示。 图3 典型参数Iwan模型力-位移图 从图3知,取5个Jenkin’s单元近似时与20个单元近似时曲线已经基本重合,因此对于单纯的迟滞非线性,考虑计算效率因素,取5个Jenkin’s单元进行近似,Jenkin’s单元个数对振动响应的影响,下文还将继续讨论。对上述表中参数的算例,其初始小位移时的振型以及5个Jenkin’s单元全部屈服后的振型[26]如图4所示。 图4 梁振型 振型表达式为: φn(x)=Ansin(knx)+Bncos(knx)+ Cnsinh(knx)+Dncosh(knx) (12) 图4中x,y轴分别为无量纲后的参数x/L,φn/Bn,可知当连接结构弹簧刚度减小时,端点有远离x轴的趋势。 显然,激励力足够大时,系统在一个振动周期内,会随着Iwan模型的加载与卸载而在各不同线性振型之间转换,转换条件为: (13) 或 (14) 式(13)中Δi为Jenkin’s单元屈服位移点,条件(13)对应如图3(b)中滑移点,条件(14)为速度反向点,如图3a中a,b点。用5阶振型对各状态进行近似,Iwan模型中Jenkin’s单元的个数为5,采用四阶Runge-Kutta法求解该算例的位移响应,仿真步长1×10-5,取10s时间历程,典型参数(激励力幅值、频率)设定下端点的1周期及2周期运动时程图、相图及振型匹配的过程图如图5所示。 图5 单周期运动梁端点状态切换时的振型映射 首先研究振型截断及Iwan模型参数设置对系统响应的影响,通过式(6),(7),系统离散为在不同状态下的S阶振动方程,改变振型的数目S,得到梁端点响应的分岔图与S之间的关系如图6,可以考察振型之间的耦合作用对系统响应的影响,以便确定合适的振型离散数目N,在计算精度与效率之间求得平衡,这里取Iwan模型的Jenkin’s单元个数不变为5。 图6 特定参数,不同的振型离散数目N,梁端点响应幅频响应图及时程图,k=4.7E3 图7 特定参数,不同的Jenkin’s单元个数,梁端点响应幅频响应图及时程图 图6中x轴变量的表达式为ω*=ω/ω1,ω为激励力频率,ω1为系统第1阶模态的基频,y轴变量w*的表达式为w*=w/s1,w为端点位移,s1为Jenkin’s单元的最小屈服位移,不同的Jenkin’s单元屈服位移是s1的整数倍。从图中可知,1振型近似与5振型近似时端点响应几乎相同,在该扫频区间仅在端点处有较小的振幅差别,且整个扫频区间内系统呈现出简单的单周期运动,随着振型数目S的增加,响应没有变复杂的趋势;特定参数时程图对比,两种振型截断个数设定下,系统响应仅有较小的幅值差别。 取振型个数S=5,改变Iwan模型中Jenkin’s单元的个数,研究其对端点响应的影响。由图3知不同的Jenkin’s单元个数影响Iwan模型的力-位移图的“光滑度”,在求系统的响应时,Jenkin’s单元个数增加会令系统在一个振动周期内模态传递的次数增加。图7中,横坐标单位表达式与图6中相同,而纵坐标表达式为w*=w/s,s在改变Jenkin’s单元个数时保持不变,为Iwan模型整体屈服时的位移。求系统响应时,微调激励力大小令共振峰幅值一致,从图7中可知,随着Jenkin’s单元个数的增加,响应的共振峰向高频移动,这是由于增加Jenkin’s单元的个数能间接减少系统刚度的损失(采用1个Jenkin’s单元时系统刚度无损失,为双线性系统),这一点由图3也可以看出,随着Jenkin’s单元个数增加,系统刚度也渐渐趋向于双线性系统。 图8 阻尼及激励力对端点响应的影响,k=4.7E3 阻尼与预紧力是影响时变非线性边界条件连续体系统振动响应的重要因素[18],如下图8a为增大阻尼对端点响应分岔图的影响,下文图中坐标ω*与w*表达式与图6(a)中相同,从图8(a)中可知: 模态阻尼比增大后,共振峰降低,随着阻尼的持续增大,共振峰会有向低频漂移的趋势;在远离共振峰的扫频区间(ω*<0.7和ω*>1.3),阻尼对系统响应幅值的影响较小;与阻尼相同,激励力大小引起的整体结构的非线性响应同样是航天工程中非常敏感的问题[3,7],改变激励力幅值大小,可得特定参数下激励力幅值对系统响应的影响如图8(b),可以看出激励力对比阻尼,全频域内对响应幅值都有明显的影响,在该系统参数设定下,随着激励的增大,系统共振峰微弱地由高频向低频漂移,这是由于迟滞非线性的存在导致系统刚度在大振幅振动时损失较大引起。 图9 阻挡弹簧刚度对端点响应的影响 端点弹簧刚度也是影响系统振动响应的重要因素之一[18],图9为改变Iwan模型刚度及系统共振峰幅值,固定其他参数得到的端点响应图。由图9知,不同的刚度设定下,随着共振峰幅值增大,系统共振峰有不同程度的向低频漂移的现象;刚度较大时,漂移程度较小,系统更加趋向于线性,共振峰幅值较大时(ω*=4.2),这一现象尤为明显。 本文利用一种解决分段线性边界条件连续体受迫振动的新方法——相对振型转换法研究了一端固支一端带有螺栓连接梁的振动响应,该法基于模态传递的思想,通过将每次状态转换后新状态各模态位移重置为0,前一状态各模态坐标处理后作为新振动方程中的参数,该方法对于一类可转变为分段线性边界条件的连续体系统均可以进行求解,具有广泛适用性。这是首次尝试用模态传递的思想来研究迟滞非线性边界条件连续体振动问题,说明振型转换思想不仅可以用来求解连续体的撞振问题,还可以应用到其他具有复杂非线性边界条件(如迟滞等)的连续体动力学响应研究中,扩展了振型转换法的适用范围。从算例结果来看,新方法具有良好的收敛性,计算精度高,计算高效,对结果进行实验验证是下一步的工作。 在本文算例的设定下,1阶与5阶振型近似在反映系统的动力学特性时差别不大,边界条件的“光滑度”对动力学响应的非线性特性具有一定的影响,力——位移图越光滑,系统动力学响应中的非线性特性也越趋向于减弱。在进行参数研究时,采用5阶振型近似,5个Jenkin’s单元对Iwan模型建模,利用端点响应的分岔图进行研究,在特定的扫频区间,系统表现出单周期运动,以及弱频率漂移非线性特性,即系统的共振峰随着激励力的增大向低频漂移,得到了阻尼、激励力幅值及端点阻挡弹簧的刚度对该类振动问题的影响,可知大阻尼对系统的非线性响应有较强的抑制作用;随着激励力的增大,系统非线性响应——频率漂移程度逐渐增大;端点弹簧的刚度影响系统频率漂移的程度,相同振幅条件下,刚度越大频漂越小,这是由于刚度较大时,即使大振幅振动时边界刚度有一定的损失,余下的刚度仍然可令系统振型接近于两端固支梁。 端点带螺栓连接梁所代表的一类系统其非线性振动问题具有实际工程背景,尤其是在研究航天器“频率漂移”机理时,研究人员关注连接结构非线性对整体结构“频率漂移”的影响。从上面设定的系统得到的研究结果看,迟滞非线性边界条件能够造成连续体产生“频漂”现象,但是其程度受端点限制(螺栓)刚度的影响较大。本文得到的结论对探讨航天器“频率漂移”现象的成因具有重要的参考价值。 [1] Bindemann A C,Ferri A A.Large amplitude vibration of a beam restrained by a non-linear sleeve joint[J].Journal of Sound and Vibration,1994,184(1): 19-34. [2] Gaul L,Lenz J.Nonlinear dynamics of structures assembled by bolted joints[J].Acta Mechanica,1997,125(1-4): 169-181. [3] Carney K.Nonlinear dynamic behavior in the cassini spacecraft modal survey[R].N20050180492,JPL,NASA,2005. [4] Bingham J G,Folkman S L.Measured influence of gravity on the dynamic behavior of a truss pinned joints[A].In: 37th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference.Salt Lake City: AIAA,1996: 1043-1053. [5] Ingham M D,Crawley E F.Microdynamic characterization of modal parameters for a deployable space structure[J].AIAA Journal,2001,39(2): 331-338. [6] Folkman S L,Rowsell E A,Ferney G D.Influence of pinned joints on damping and dynamic behavior of a truss[J].Journal of Guidance,Control,and Dynamics,1995,18(6): 1398-1403. [7] Okuizumi N.Nonlinear vibration of a satellite truss structure with gaps[A].In: 45th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference.California: Palm Springs,2004: 19-22. [8] Hartwigsen C J,Song Y,McFarland D M,et al.Experimental study of non-linear effects in a typical shear lap joints configuration[J].Journal of Sound and Vibration,2004,277(1-2): 327-351. [9] Ouyang H,Oldfield M J,Mottershead J E.Experimental and theoretical studies of a bolted joint excited by a torsional dynamic load[J].International Journal of Mechanical Sciences,2006,48(12):1447-1455. [10] Heller L,Foltete E,Piranda J.Experimental identification of nonlinear dynamic properties of built-up structures[J].Journal of Sound and Vibration,2009,327(1-2): 183-196. [11] Iwan W D.A distributed-element modal for hysteresis and its steady-state dynamic response[J].Journal of Applied Mechanics,1966,33(4): 893-900. [12] Segalman D J,Starr M J.Inversion of Masing models via continuous Iwan systems[J].International Journal of Non-Linear Mechanics,2008,43(1): 74-80. [13] Argatov I I,Butcher E A.On the Iwan models for lap-type bolted joints[J].International Journal of Non-Linear Mechanics,2011,46(2): 347-356. [14] Lubarda V A,Sumarac D,Krajcinovic D.Preisach model and hysteretic behaviour of ductile materials[J].Eur.J.Mech.ASolids,1993,12(4): 445-470. [15] Moon F C,Shaw S W.Chaotic vibrations of a beam with non-linear boundary conditions[J].International Journal of Non-Linear Mechanics,1983,18(6): 465-477. [16] Shaw S W.Forced vibrations of a beam with one-side amplitude constraint: theory and experiment[J].Journal of Sound and Vibration,1985,99(2): 199-212. [17] Tsai Hsiangchuan,Wu Mingkuen.Methods to compute dynamic response of a cantilever with a stop to limit motion[J].Computers & Structures,1996,58(5): 859-867. [18] Ervin E K,Wickert J A.Repetitive impact response of a beam structure subjected to harmonic base excitation[J].Journal of Sound and Vibration,2007,307(1-2): 2-19. [19] Ervin E K,Wickert J A.Experiments on a beam-rigid body structure repetitively impacting a rod[J].Nonlinear Dynamics,2007,50(3): 701-716. [20] Shih P J,Shih W P.Impact dynamics of vibratory microprobe for microcoordinate measurement[J].Journal of Applied Physics,2007,101(11): 113516. [21] Brake M R,Wickert J A.Modal analysis of a continuous gyroscopic second-order system with nonlinear constraints[J].Journal of Sound and Vibration,2010,329(7): 893-911. [22] Brake M R.A hybrid approach for the modal analysis of continuous systems with discrete piecewise-linear constraints[J].Journal of Sound and Vibration,2011,330(13): 3196-3221. [23] Wei H T,Kong X R,Wang B L,et al.An approach for vibration analysis of continuous system with piece-wise-linear boundary conditions[J].Acta Aeronautica et Astronautica Sinica,2011,32(12):2236-2243. [24] Segalman D J.A four-parameter Iwan model for lap-type joints[J].J.Appl.Mech,2005,72(5): 752-761. [25] Song Y,Hartwigsen C J,McFarland D M,et al.Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements[J].Journal of Sound and Vibration,2004,273(1-2): 249-276. [26] Wiedemann S M.Natural frequencies and mode shapes of arbitrary beam structures with arbitrary boundary conditions[J].Journal of Sound and Vibration,2007,300(1-2): 280-291.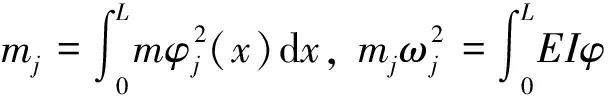

2 数值求解及讨论
2.1 算例梁受迫振动响应及讨论

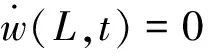

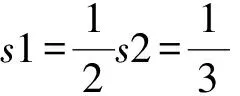
2.2 振型耦合、Jenkin’s单元个数对响应的影响


2.3 阻尼、激励力幅值及端点螺栓连接刚度对响应的影响

3 结 论
