强侧风下桥上高速列车倾覆稳定性及最优风障高度的研究
2014-09-18项超群郭文华张佳文
项超群,郭文华,2,张佳文
(1.中南大学 土木工程学院,长沙 410004;2.中南大学 高速铁路建造技术国家工程实验室,长沙 410004)
为满足安全、高效、可靠的交通运输体系的需要,我国高速铁路建设发展迅速。减轻列车的重量对于其加速性能、轮轨磨耗等方面具有重要意义,故轻质高强材料在列车中得到了广泛应用,但与此同时侧风产生的气动力对其运营安全的影响急剧增加[1-2]。从地形地质条件、变形、沉降和行车平顺性等方面综合考虑,高速铁路建造过程中桥梁占线路总长度的比例越来越大,如京沪高速铁路中桥梁长度占了线路总长的80.7%[3]。主梁线路相对路基较高,当列车在桥梁上运行时侧风对其影响更加显著[4]。
为保证侧风下列车运行的安全性,通常采用的措施包括运行管制和设置风障[5]。运行管制即当侧风超过一定值后限制行车速度或车辆停运,由此必将影响列车的运输效率。蒋崇文等[6]计算了列车在不同等级风速下的气动力,结果表明在12级大风作用下侧倾力矩将使列车发生侧翻。高广军等[7]计算了运行于桥梁上的列车在不同车速下的临界倾覆风速,指出随车速的提高临界风速迅速降低。日本的Nemuro线曾在出现列车脱轨事故后,在桥梁上安装了风障,之后列车限速运行或暂停事故大大减少,说明合理的风障设计在保证安全的前提下能有效提高列车的运输效率[8]。陈涛[9]根据列车运行于桥梁上的气动力系数,计算了某一风障高度下列车运行于直线轨道的临界车速,并与不设置风障进行了对比,指出加设风障能显著地提高列车运行速度。唐煜[10]对背风侧轮轨接触轴线的力矩定义了轮重减载率,计算了4m高风障下,侧风从弯道内侧吹向列车时的临界风速,指出风障的设置能显著提高临界风速值,但研究中未考虑轨道超高使列车产生倾斜时对列车气动力系数的影响。目前的研究一般只针对特定风障高度进行计算,而对风障高度的优化研究较少。
本文基于大型流体计算通用软件FLUENT,考虑轨道超高引起的列车风攻角、列车位于桥梁的不同横向位置、合成风的风偏角等因素,计算了列车运行于不同风障高度简支箱梁桥上时的气动力系数。根据列车通过弯道时的受力特征分别对迎风侧轮轨接触轴线和背风侧轮轨接触轴线定义倾覆系数,并参考相关标准设定列车倾覆系数的容许值。最后据此研究列车以不同速度通过高速铁路简支箱梁桥时需要设置的最优风障高度。
1 高速列车气动力系数计算
1.1 计算模型及参数设置
高速铁路桥梁中,使用最广泛的是简支箱梁,研究中桥梁几何模型采用京沪高速铁路中32 m双线简支箱梁。桥墩对列车的气动力影响很小[9],在计算模型中忽略其影响。车辆在曲线轨道上运行时将产生离心力,为平衡离心力作用需设置超高,从而借助车辆重力的水平分力抵消离心力,当曲线上无渣轨道布置于简支箱梁桥上时,一般将无渣轨道板倾斜。为了便于对流场划分网格,模型中将桥面轨道板等细部构造进行了简化。将风障简化为直立于桥梁两侧的平板,当侧风从弯道内侧吹来,即迎风侧轨道低于背风侧轨道时,设置有风障的简支梁桥横截面见图1(a)所示。由于列车是一个长细比很大的几何体,其中间车辆几何外形相同,当气流流过车头一定距离后,绕流边界层的结构已趋于稳定,车辆气动力变化也趋于稳定,因此在数值模拟中常采用一节头车、一节拖车和一节尾车的三节车模型,并忽略转向架和风挡等复杂结构[11]。本文采用的高速列车均匀段横截面尺寸见图1(b)所示。轨道板倾斜将使列车通过时具有同样的倾斜角,图1(b)中,o'-x'y'z'为固定于列车车体的坐标系,其z'轴为列车的竖向中心线,o-xyz为用于计算气动力系数的坐标系,其x轴沿水平方向,在此定义∠xox'为列车风攻角。图1(b)中迎风侧轨道低于背风侧,列车风攻角为正。

图1 横截面尺寸/mFig.1 Cross section size
RNG k-ε湍流模型能较好地模拟钝体绕流问题,并且硬件要求相对较低,计算量相对较小[12],本文的计算中均采用该模型。车桥耦合体系气动特性对雷诺数的变化不敏感,由于雷诺数差异导致的气动力系数差异可以忽略不计,车桥模型采用1∶20的缩尺比。影响CFD计算结果的因素较多,其中最为重要的是计算域尺寸,计算风偏角90°情况下横桥向出口离桥梁背风侧为8、10、12、14倍桥梁宽度,横桥向入口离桥梁迎风侧对应为4、5、6、7倍桥梁宽度时列车的侧力、升力和侧倾力矩,结果表明后三种计算域所得的气动力、气动力矩相差较小,综合考虑计算精度和效率选取计算域尺寸如图2所示。为了尽可能细划车身附近网格提高结果的精确性,采用双重加密框,并定义尺寸函数使网格尺寸从列车车身周围到远离列车的区域以一定比例均匀增加。高速列车头部和尾部流线型特征明显,且其直接迎着或拖拽气体运动,其附近区域流场变化梯度最大,模型中该区域网格最小单元尺寸设为8 mm。列车和桥梁表面存在边界层效应的影响,均设为有摩擦的壁面。

图2 计算域及整体坐标系Fig.2 Computational domain and global coordinate system
计算采用的整体坐标系如图2所示,设定列车沿y轴正向行驶,侧风沿x轴正向。采用相对运动条件模拟列车周围的流场,即假设列车静止,来流速度为列车运行的反向等值速度与侧风速度的矢量合成[13],列车运行于双线简支箱梁桥迎风侧线路时合成风如图3所示。在计算域中设定ABCD面和AEHD面为合成风的速度入口边界条件,设置湍流强度0.5%、湍流粘度比10%[11]。EFGH面和BFGC面设为表压为0的压力出口边界条件。计算中待迭代残差小于10-4,且侧力、升力和侧倾力矩监视曲线平稳后认为计算收敛。
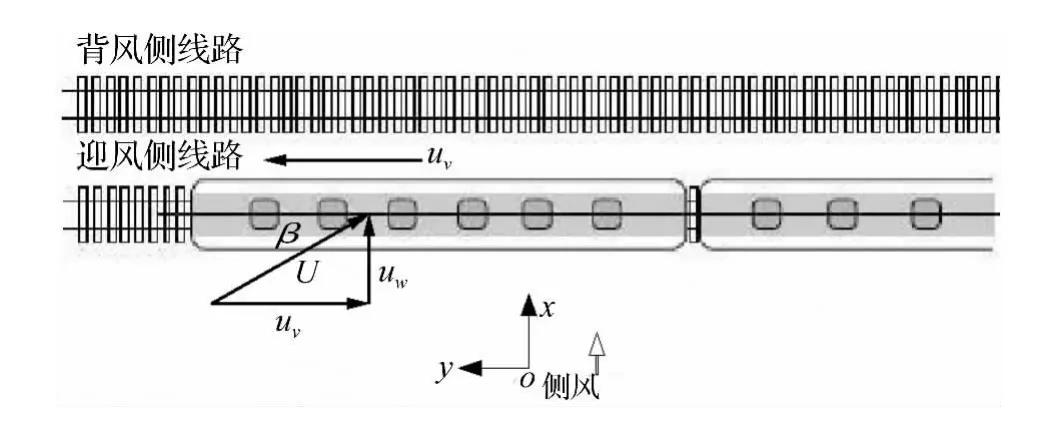
图3 合成风示意图Fig.3 Diagram of the resultant wind
1.2 气动力系数的定义
强侧风作用下,桥上列车发生侧翻、脱轨等事故主要与列车高速运动和侧风共同作用引起的气动侧力、升力和侧倾力矩有关[2,6]。列车风攻角θ和合成风的风偏角β对列车气动力有直接关系,由此根据图2的整体坐标系定义列车的气动力系数:
侧力系数:
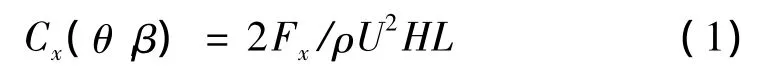
升力系数:

侧倾力矩系数:

式中,ρ为来流密度,取 1.225 kg/m3uv为列车的行车速度,uw为垂直于列车轴线的侧风风速,风偏角β=arctan(uw/uv)。侧倾力矩中心为列车几何中心。B、H分别为列车的宽度和高度,L为列车的长度。
1.3 气动力系数计算结果分析
高速运行于桥梁上的列车,在强侧风下其头车最容易发生倾覆,对列车进行行车安全性分析时主要考虑头车的倾覆稳定性[14]。根据《京津城际铁路技术管理暂行办法》和《铁路200~250 km/h既有线技术管理暂行办法》等相关规定,严禁动车组进入风区的临界风速为30 m/s。研究中假定侧风风速为30 m/s,当车速分别为 150 km/h、200 km/h、250 km/h、300 km/h、350 km/h、400 km/h 时,合成风的风偏角分别为 35.75°、28.37°、23.36°、19.80°、17.15°、15.11°。假定轨道超高150 mm,当侧风分别从弯道外侧、内侧吹向列车时风攻角 θ分别为 -5.97°、5.97°,当侧风吹向运行于直线轨道的列车时列车风攻角β为0°。研究中计算了不同风攻角、列车处于桥面不同横向位置、不同风障高度、不同风偏角下的列车气动力系数。

图4 列车运行于迎风侧线路时气动力系数随风障高度及风偏角的变化(θ=0°)Fig.4 The variation of aerodynamic coefficients of train with the height of wind barriers and incidence angle when train run on the windward line

图5 列车运行于背风侧线路时气动力系数随风障高度及风偏角的变化(θ=0°)Fig.5 The variation of aerodynamic coefficients of train with the height ofwind barriers and incidence angle when train run on the leeward line

图6 列车气动力系数随风障高度及列车风攻角的变化(β=17.15°)Fig.6 The variation of aerodynamic coefficients of train with the height of wind barriers and attack angle of train
列车运行于直线轨道时(θ=0°),其气动力系数随风障高度及风偏角的变化曲线见图4~5。由计算结果可知:① 随风障高度的增加,侧力将由顺侧风方向变为与侧风相反的方向,升力将由使列车上浮作用变为向下的负升力,侧倾力矩则由y轴左手螺旋方向变为右手螺旋方向,且气动力系数在风障较低时随其高度变化更明显;② 风障高度较小时,列车的侧力系数和升力系数均为正,且随风偏角的增大而增大,侧倾力矩系数为负,随风偏角的增大其绝对值增大。随着风障高度的增加,气动力系数对风偏角的敏感性降低;③ 当列车运行于双线桥梁迎风侧线路时,其所受气动力比背风侧线路大,该规律在没有设置风障时与文献[5,15]进行的风洞实验结论一致。
以风偏角β=17.15°为例,列车气动力系数随风障高度及列车风攻角的变化曲线见图6。可以看出:① 随风障高度的增加,风攻角对列车气动力系数的影响逐渐减小;② 列车风攻角主要影响列车的升力系数,在列车处于迎风侧线路、无风障情况下,θ=-5.97°时升力系数最小,约为 θ=5.97°的70%。
2 列车倾覆稳定性计算
当列车运行于弯道上时,作用于其上的荷载主要包括:车辆通过曲线时的离心力,由车辆振动产生的横向惯性力和竖向惯性力,合成风作用下由车体表面的分布压力和粘性力经积分产生的气动侧力、升力和侧倾力矩,因外轨超高引起的重力在车辆竖向和横向的分力。其中重力对列车总是起稳定作用,在此将其它外荷载对列车产生的倾覆力矩与重力产生的稳定力矩之比定义为倾覆系数,即:

从气动力计算结果可知,在不同的风障高度下作用于列车的气动力可能改变作用方向,且横向振动加速度方向不同时对列车的矩也不同,因此必须分别考虑列车对迎风侧轮轨接触轴线与背风侧轮轨接触轴线的倾覆安全性。对于双线简支箱梁桥,当列车处于迎风侧线路或背风侧线路时所受气动力不同,为了得出最优的风障高度必须兼顾两线路上列车的安全性。车辆倾覆包括向弯道内侧倾覆、向弯道外侧倾覆和在直线上倾覆。当侧风从弯道不同侧面吹入时列车最不利受力情况不同,其中风从弯道内侧吹向列车,横向振动加速度指向线路外侧时车辆的受力见图7所示。

图7 倾覆系数计算示意图Fig.7 Diagram of calculation for overturning coefficient
根据侧风吹向列车的方向和横向振动加速度方向,倾覆系数可展开如下:

式中:j=0、1分别表示侧风从弯道内侧、外侧吹向列车;i=0、1表示对背风侧、迎风侧轮轨接触轴线取矩;Fc=mu/R为列车受到的离心力;m为列车的质量,G=mg为列车的重力,取m=44t;uv为列车的运行速度;R为轨道的曲线半径,取R=7 000 m;Fih=maih,aih=0.1 g 为列车的横向振动加速度,Fiv=maiv,aiv=0.13 g为列车的垂向振动加速度[16];Fx,Fz和 My分别为列车受到的气动侧力、升力和侧倾力矩,根据列车运行速度uv、侧风速度uw、风偏角β及列车风攻角θ计算。θ根据轨道超高求得,计算中取超高150 mm。为了保证车辆不发生倾覆,倾覆系数D不能超过容许值,参考《铁道车辆动力学性能评定和试验鉴定规范》和《高速试验列车客车强度及动力学规范》取容许倾覆系数[D]=0.8。设以上公式的离心力Fc=0、列车风攻角θ=0°即可得出列车运行于直线线路上的倾覆系数计算公式。当列车受到的重力以外的荷载对轮轨接触轴线产生的力矩与重力的力矩方向相同时,将出现D<0的情况,此时取D=0,即列车不会倾覆。
3 最优风障高度的选取
从对列车气动力系数的分析可知,风攻角对升力系数的影响不能忽略,在此考虑风攻角的影响,计算列车在不同运行环境下的倾覆系数,并据此选择最优风障高度。当列车在弯道上运行时,由于曲线半径(R=7 000 M)远大于桥梁跨径(L=32 M),因此认为采用直线线路模型计算的气动力系数应用于曲线线路时所引起的误差足够小。考虑到列车在桥上的横向位置以及迎风侧、背风侧轮轨接触轴线等因素,各车速在每种风障高度下包括4种计算工况,在此定义各工况如下:工况1(列车处于迎风侧线路,对迎风侧轮轨接触轴线取距);工况2(列车处于迎风侧线路,对背风侧轮轨接触轴线取距);工况3(列车处于背风侧线路,对迎风侧轮轨接触轴线取距);工况4(列车处于背风侧线路,对背风侧轮轨接触轴线取距)。
3.1 侧风从弯道内侧吹向列车
当30 m/s的侧风从弯道内侧吹向列车时,计算以不同速度运行的列车在各风障高度下的倾覆系数见图8。

图8 风从弯道内侧吹向列车时的倾覆系数Fig.8 Overturning coefficients when the blows from the inside of curve
计算可知:对于迎风侧轮轨接触轴线,当车速较高时倾覆系数为0,表明当车速较高时外荷载对迎风侧轴线的力矩与重力矩同向,即列车不会朝弯道内侧倾覆。随着车速减小,列车受到的离心力减小,故而倾覆系数增大。同理随着风障高度的增加列车受到的气动力减小,倾覆系数也增大。但当列车处于迎风侧线路上风障高度超过4.0 m后倾覆系数反而下降,该现象是侧力系数在4.0 m后变化趋势发生了改变引起的。在计算的范围内,对于迎风侧轮轨接触轴线倾覆系数均小于0.8,即对于该轴线列车均是安全的;对于背风侧轮轨接触轴线,车速越高倾覆系数越大,但风障能有效降低倾覆的危险性;对比分析列车处于两线路上,各行车速度下倾覆系数低于容许倾覆系数的最小风障高度可知,列车处于迎风侧线路上时需设置的风障高度均比背风侧线路高0.5 m,即迎风侧线路为选择风障高度的控制线路。
3.2 侧风从弯道外侧吹向列车
当侧风从弯道外侧吹向列车时,一般情况下气动侧力与弯道上列车高速运动产生的离心力方向相反,但当风障过高时,气动侧力则可能与离心力方向相同。计算不同风障高度下,30 m/s的侧风从弯道外侧吹向列车时的倾覆系数见图9。
计算可知:对于迎风侧轮轨接触轴线,倾覆系数随行车速度的提高和风障高度的增加而增加。当列车处于背风侧线路上、速度为400 km/h、风障高度为5.0 m时倾覆系数超过容许值,说明过高的风障可能使列车朝迎风侧侧翻;对于背风侧轮轨接触轴线,当风障较低时,两线路上各车速的倾覆系数均超出容许范围,即在风障较低、侧风风速为30 m/s时列车不能通过该弯道。设置风障能有效减小列车对背风侧轮轨接触轴线的倾覆系数,但当列车处于迎风侧线路上时,风障高度超过4.0 m后倾覆系数反而增加,对于背风侧线路则不断减小;从图9可知当列车处于迎风侧线路上时需设置的风障比背风侧线路高。

图9 风从弯道外侧吹向列车时的倾覆系数Fig.9 Overturning coefficients when the blows from the outside of curve
3.3 侧风吹向直线轨道列车
当列车运行于直线轨道上时,不再受到离心力的作用,同时直线轨道也不需设置超高。计算列车以不同速度运行于直线轨道上,受到30 m/s的侧风时的倾覆系数见图10。
计算可知:对于迎风侧轮轨接触轴线,随着风障高度的增加,倾覆系数逐渐增加但都在容许的范围内;对于背风侧轮轨接触轴线,当风障高度较低时,各车速下的倾覆系数均超出容许值,随风障高度的增加倾覆系数均得到了减小且各车速下的系数越来越接近,当风障高度为4.5 m时,两线路上列车的倾覆系数曲线均相交于一点;对比两线路上满足不同车速下列车倾覆安全性要求的风障高度可知,当列车处于迎风侧线路上时需设置的风障比背风侧高。

图10 列车运行于直线轨道上的倾覆系数Fig.10 Overturning coefficients when the train runs the straight track
分析可知,当列车处于迎风侧线路上时需设置的风障均比背风侧线路高。根据图8~图10,对于常年主导风向较稳定的桥梁,列车以不同速度运行时需要设置的风障高度如表1。而对于强侧风从弯道两侧都可能吹入的情况,应综合弯道内道和弯道外侧取较大值。

表1 最优风障高度Tab.1 The optimal height of wind barriers/m
4 结论
(1)对于双线简支箱梁桥,当列车运行于迎风侧线路时所受气动力比背风侧线路大。当列车通过设置了轨道超高的桥梁时,列车风攻角对升力系数影响较大。
(2)对迎风侧轮轨接触轴线的倾覆系数随风障高度的增加而增加,故过高的风障可能使列车向迎风侧倾覆。当风障较低时,对背风侧轮轨接触轴线的倾覆系数比迎风侧大,但随风障高度的增加迅速降低。因此综合考虑迎风侧和背风侧轴线必存在最优风障高度。
(3)对运行于双线简支箱梁桥上的列车,分别考虑其位于不同线路时的倾覆系数得知,当列车处于迎风侧线路上时需设置的风障高度均比处于背风侧线路时高,即迎风侧线路是风障高度设置的控制线路。
(4)对于主导风向稳定的桥位,综合考虑列车处于双线桥梁的两线路上、对迎风侧和背风侧轮轨接触轴线的倾覆系数,得出了不同弯道上、列车以不同速度运行时的最优风障高度。对于侧风从弯道两侧都可能吹入的情况,应综合弯道内侧和弯道外侧取较大值。
[1]Carrarini A.Reliability based analysis of the crosswind stability[J].Journal of Wind Engineering and Industrial Aerodynamics,2007,95:493-509.
[2]田红旗.中国列车空气动力学研究进展[J].交通运输工程学报,2006,6(1):1-9.TIAN Hong-qi.Study evolvement of train aerodynamics in china[J].Journal of Traffic and Transportation Engineering,2006,6(1):1 -9.
[3]孙树礼.京沪高速铁路桥梁工程[J].铁道标准设计,2008,6:1-4.SUN Shu-li.Bridge engineering in the Beijing-Shanghai highspeed railway[J].Railway Standard Design,2008,6:1-4.
[4]Raghunathan R S,Kim H D,Setoguchi T.Aerodynamics of high-speed railway train [J]. Progress in Aerospace Sciences,2002,38(6-7):469-514.
[5]刘庆宽,杜彦良,乔富贵.日本列车横风和强风对策研究[J].铁道学报,2008,30(1):82-88.LIU Qing-kuan, DU Yan-liang, QIAO Fu-gui. Traincrosswind and strong wind countermeasure research in Japan[J].Journal of the China Railway Society,2008,30(1):82-88.
[6]蒋崇文,张劲柏,关雪梅,等.横风强度对平原上集装箱列车横向稳定性的影响[J].铁道学报,2011,33(3):17-22.JIANG Chong-wen,ZHANG Jin-bai,GUAN Xue-mei,et al.Influence of crosswind intensity on cross stability of container trains running on plain[J].Journal of the China Railway Society,2011,33(3):17 -22.
[7]高广军,李鹏.青藏线上集装箱平车在强横风下的稳定性[J].中南大学学报(自然科学版),2011,42(2):533-538.GAO Guang-jun,LI Peng.Running stability of container car in Qing Hai-Tibet railway line[J].Journal of Central South University(Science and Technology),2011,42(2):533-538.
[8]董香婷,党向鹏.风障对侧风作用下列车行车安全影响的数值模拟研究[J].铁道学报,2008,30(5):36-40.DONG Xiang-ting,DANG Xiang-peng.Study on influence of wind barriers on traffic safety of trains under crosswind by numerical simulation[J].Journal of the China Railway Society,2008,30(5):36-40.
[9]陈涛.高速铁路桥梁风障设置对列车及主梁气动性能影响研究[D].长沙:中南大学土木工程学院,2011.
[10]唐煜.桥梁挡风屏对强侧风条件下列车运营安全性的影响[D].成都:西南交通大学土木工程学院,2010.
[11]罗建斌,胡爱军.高架桥声屏障高度对列车气动特性影响的数值模拟[J].计算物理,2012,29(1):65-72.LUO Jian-bin,HU Ai-jun.Numerical study of the effect of viaduct noise barrier height on train aerodynamic characteristics[J]. Chinese Journal of Computational Physics,2012,29(1):65 -72.
[12]周奇,朱乐东,郭震山.曲线风障对桥面风环境影响的数值模拟[J].武汉理工大学学报,2010,32(10):38-44.ZHOU Qi, ZHU Le-dong, GUO Zhen-shan. Numerical simulation for curve windshield barrier effects on wind environment around bridge deck[J].Journal of Wuhan University of Technology,2010,32(10):38 -44.
[13]毛军,郗艳红,杨国伟.侧风风场特征对高速列车气动性能作用的研究[J].铁道学报,2011,33(4):22-30.MAO Jun,XI Yan-hong,YANG Guo-wei.Research on influence of characteristics of cross wind field on aerodynamic performance of a high-speed train[J].Journal of the China Railway Society,2011,33(4):22 -30.
[14]Cheli F,Corradi R,Rocchi D,et al.Wind tunnel tests on train scale models to investigate the effect of infrastructure scenario[J].Journal of Wind Engineering and Industrial Aerodynamics,2010,98:353-362.
[15]Suzuki M,Tanemoto K,Maeda T.Aerodynamic characteristics of train/vehicles under cross winds[J].Journal of Wind Engineering and Industrial Aerodynamics,2003,91:209-218.
[16]翟婉明.车辆-轨道耦合动力学(第三版)[M].北京:科学出版社,2007.
