高速列车系统动力学空气弹簧建模方法研究

戚 壮，李 芾，黄运华，虞大联

(1.西南交通大学 机械工程学院，成都 610031;2.南车青岛四方股份 国家工程实验室，山东 青岛 266111)

作为二系悬挂装置，空气弹簧目前已广泛应用于现代高速列车上。由于空气弹簧是一个多物理变量的非线性系统，如何在高速列车动力学计算中建立空气弹簧模型，已成为国内外学者研究的焦点。

Oda等［1］利用“弹性支撑阻尼”系统建立了适用于更宽频域范围的“Nishimura”模型，但是该模型并没有考虑气体在管路中的惯性效应。Krettek等［2］基于流体力学与气动力学原理，简化了空气弹簧的计算公式，建立了空气弹簧非线性气动模型。Nieto等［3－5］基于空气热动力学原理，对橡胶气囊、附加空气室、节流孔和其间的连接管路分别进行建模，再将其用统一的微分方程组进行描述。这类模型考虑了空气弹簧内部气体的运动特性以及温度、压强的变化对空气弹簧动态特性的影响，可称为空气弹簧的完全模型。

我国将空气弹簧广泛应用于轨道车辆只有20多年的时间［6］，但已有诸多学者对空气弹簧的建模方法进行了卓有成效的研究。李芾等［7］基于热力学及流体力学理论，推导了空气弹簧物理模型的统一数学表达式。张广世等［8］基于SIMULINK平台，建立了带有连接管路的空气弹簧动力学模型。张利国等［9］对空气弹簧的现状及其发展作了综述性总结。王家胜等［10］对空气弹簧的动刚度进行了线性化研究。但是，在国内大部分高速列车动力学计算中，空气弹簧仍采用线性模型［11］。

综上所述，高速列车动力学计算中空气弹簧的建模方法主要分为三类:线性模型、非线性模型和完全模型。这三类模型对动力学计算结果有何影响，正是以下研究的主要内容。

1 空气弹簧动力学模型

1.1 线性模型

线性模型是将空气弹簧的动刚度和动阻尼等效为一个钢弹簧并联一个阻尼器，如图1所示，其中钢弹簧的等效刚度Ke与阻尼器的等效阻尼Ce均为定值，由空气弹簧的动刚度试验确定。由于线性模型建模简便、参数直观、计算速度快，该模型目前广泛应用于高速列车的动力学计算中。

图1 空气弹簧线性模型Fig.1 The linear model of air spring

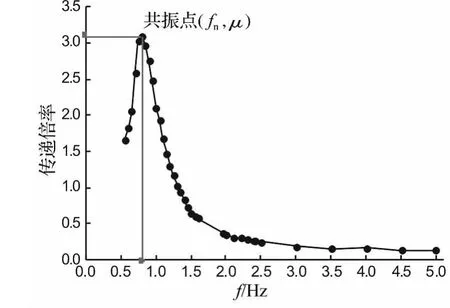
图2 空气弹簧振动特性曲线Fig.2 The vibration character curve of air spring

空气弹簧线性模型中的等效刚度Ke与等效阻尼Ce需要对空气弹簧进行动刚度试验确定。根据相关标准［12］对空气弹簧进行动刚度试验。在空气弹簧上面放置一个摩擦力极小并作垂直方向导向的秤锤，该秤锤的质量m要使空气弹簧内压力达到空气弹簧正常使用时的要求。在空气弹簧底部施加频率为0.5－5 Hz，振幅为3 mm的简谐振动，测量空气弹簧上秤锤的垂向振幅，并以加振频率为x轴，秤锤振幅与加振振幅的比(传递倍率)为y轴，得到某次试验中空气弹簧的振动特性曲线如图2所示。

根据振动特性曲线，可以得到该空气弹簧的共振点。共振点的横坐标对应共振频率fn，纵坐标对应共振倍率μ。则其等效刚度Ke和等效阻尼Ce分别由下式进行计算［12］:

式中，π为圆周率常数。

1.2 非线性模型

基于流体力学和气动力学原理，可以建立描述空气弹簧内部气体运动的微分方程组，从而建立空气弹簧的非线性模型［2，7］。非线性模型将橡胶气囊与附加空气室中气体的热动力学变化过程视为等熵过程，满足气体的多变过程方程:

式中:i=b时，表示橡胶气囊，i=t时，表示附加空气室;0为表示某一物理量的初始状态;pi为橡胶气囊或附加空气室内部压强(Pa);Vi为橡胶气囊或附加空气室容积(m3);n为气体的多变指数，在绝热过程中取1.4。

将橡胶气囊与附加空气室内部的气动力学方程进行联立，并将微分方程线性化，可得到橡胶气囊内部压强的表达式为:

式中:Ae为空气弹簧的有效面积(m2);A为橡胶气囊与附加空气室之间连接管路的截面积(m2);x为连接管路中气体的位移(m);z为空气弹簧上下表面的距离(m)。

橡胶气囊与附加空气室之间连接管路中的气体视为恒定质量块在管路中的运动，考虑气体的惯性效应和气体与管壁的摩擦损耗，基于流体力学公式，可得到管内气体的运动方程为:

式中:mp为管内气体的质量(kg);ρ为管内气体的密度(kg/m3);λ为沿程阻力系数;ζ为局部阻力系数;L为连接管路长度(m);d为连接管路内径(m)。

考虑到橡胶气囊自身具有的阻尼作用，其对车体的支撑力以及对构架的反力F的表达式为:

式中:p0为大气压强(Pa);Cb为橡胶气囊自身阻尼(N·s/m)。

此外，对于应急橡胶堆，当空气弹簧的上下表面没有贴靠时，即z＞0时，由于其刚度远大于空气弹簧的刚度，可认为应急橡胶堆不起作用;当空气弹簧的上下表面开始贴靠时，即z=0时，可将应急橡胶堆视为刚度Kr与阻尼 Cr并联的线性力元。因此，联立式(4)－(6)，即可建立如图3所示的空气弹簧的非线性模型。

图3 空气弹簧非线性模型Fig.3 The non-linear model of air spring

1.3 完全模型

完全模型需要对空气弹簧悬挂系统的各个部件分别进行建模［3－5］，其中包括橡胶气囊、附加空气室、节流孔、高度调整阀、差压阀等。描述橡胶气囊和附加空气室的数学方程可参考(4)式。基于空气动力学原理，重新建立的气体流经节流孔的运动方程如下式:

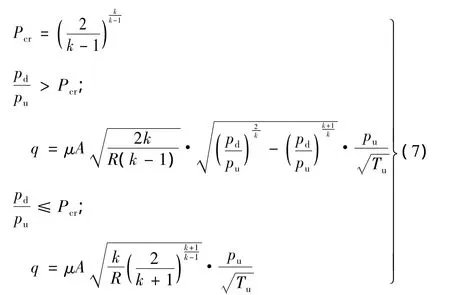
式中:Pcr为气体的临界压力比，用来判断气体的流速是否大于声速;pd，pu为分别为节流孔下游和上游的绝对压强(Pa);Tu为节流孔上游温度(K);μ为流量系数，一般μ＜1，由试验确定;A为节流孔面积(m2);R为理想气体常数，一般取287.1 J/(kg·K);k为气体的比热比，一般取1.4;q为气体流经节流孔的流量(kg/s)。

当车体高度超出高度调整阀的无感区后，高度调整阀在一定的延迟时间后打开，对橡胶气囊进行充气或放气，以调整车体高度。根据高度调整阀的动作特性，其数学模型可等效为一个二阶系统的传递函数，如下式:

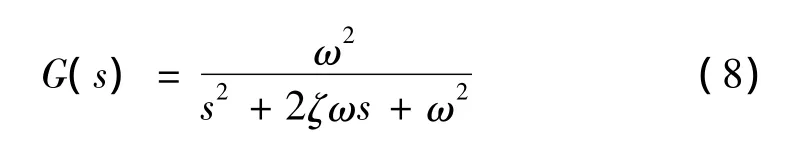
式中:G(s)为高度调整阀模型的传递函数;s为拉普拉斯变换后的变量;ω，、ζ为高度调整阀模型中的参数。

当两侧空气弹簧压强差超出预定范围时，差压阀打开，气体从高压侧流向低压侧，以保证车辆的运行安全。差压阀的数学方程可表示为:

式中:pg为差压阀预先设定的压强差(Pa);pd，pu为分别为差压阀下游和上游的绝对压强(Pa);M·为气体流经差压阀的流量(kg/s)，可通过(7)式计算。

此外，完全模型还考虑了空气弹簧内部气体与外界的热量交换，其交换热量按照下式计算:

式中:i为表示空气弹簧的不同部分，i=b时，表示橡胶气囊;i=t时，表示附加空气室;i=p时，表示连接管路;Qi为内部气体与外界的热交换功率(W);γi为不同位置的导热系数(W/(m.K));Si为不同位置的热交换面积(m2);Ti为不同位置的温度(K);Ta为外界大气温度(K);εi为管壁、气囊或附加气室壁的法向厚度(m);

将式(7)～式(10)与式(4)和式(6)联立，即可建立空气弹簧的完全模型。由于完全模型涉及的物理量较多，可在AMESim平台上构建，如图4所示。

图4 空气弹簧完全模型Fig.4 The complete model of air spring

2 准静态动力学特性

2.1 激振载荷的确定

为了便于对比，计算中均以某型动车组及其空气弹簧为算例，该型车空气弹簧主要结构参数与车辆主要动力学参数见表1。

表1 数值计算中的主要参数Tab.1 Main parameters of numerical calculation

为了确定在准静态动力学特性分析中对空气弹簧施加的激振载荷，首先以传统方法对该型高速动车组进行动力学计算。在仿真中设定，轨道谱为京津高铁实测轨道谱，车辆在40 s内以350 km/h的速度在平直线路上作匀速运动。在计算结果中，取出车体与构架之间在空气弹簧处相对位移的时间历程，如图5(a)所示。该相对位移即可视为高速列车在运行的过程中对空气弹簧的激励。由激振的时间历程可知，对空气弹簧的激振幅值大部分集中于3 mm左右。对激振的时间历程进行快速傅立叶变换，如图5(b)所示，激振频率主要集中在1 Hz左右。因此，在准静态动力学特性分析中，选取振幅为3 mm，频率为1 Hz的正弦波作为空气弹簧的激振。

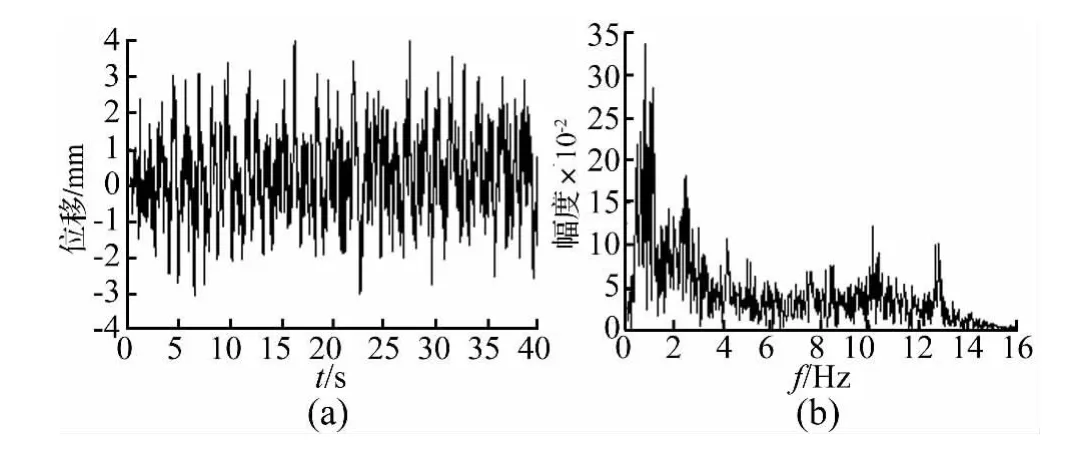
图5 空气弹簧激振的时间历程及快速傅里叶变换Fig.5 The time history of excitation to the air spring and its Fourier transformation

2.2 准静态动力学仿真

将空气弹簧的上表面固定，并预加载车体对空气弹簧的静态压力。对空气弹簧的下部施加振幅为3 mm，频率为1 Hz的正弦激励，测量空气弹簧上表面对车体支撑力的变化。三种模型的力—位移回滞曲线如图6所示。

图6 三种空气弹簧动力学模型的回滞曲线Fig.6 The hysteresis curves of the three dynamic models of air spring

由该回滞曲线可以看出，线性模型的回滞曲线呈椭圆形，且包围了更大的面积，说明线性模型具有较高的阻尼特性。非线性模型和完全模型回滞曲线的形状较相似，与线性模型的椭圆形回滞曲线相比，前两者模型回滞曲线的两端较尖扁。这体现了空气弹簧的非线性特性。因此，在准静态仿真中已可以看出这三种空气弹簧动力学模型动态特性的差异，但是这些差异究竟会对高速列车的动力学计算产生何种影响，还需要在整车动力学计算中进行探究。

3 整车动力学性能研究

将三种空气弹簧动力学模型引入前述高速动车组的整车动力学模型中，根据《高速动车组整车试验规范》［13］对其进行动力学计算，以研究在不同空气弹簧动力学模型下高速动车组的动力学性能。

3.1 车辆运行安全性的计算

首先计算在三种空气弹簧动力学模型下高速动车组通过曲线时的运行安全性。设定车辆通过的曲线半径为7 000 m，缓和曲线的长度为670 m，曲线超高为150 mm，轨道不平顺激励为京津城际高铁轨道谱。计算车辆以不同的速度通过该曲线时，轮轨垂向力、轮轴横向力、脱轨系数、轮重减载率和倾覆系数最大值，如图7所示。

由图7的计算结果可以看出，三种模型计算出的车辆运行安全性指标基本一致。以完全模型为参照，非线性模型与线性模型相比于完全模型在各种速度级下的最大相对误差如图8所示。由相对误差的对比可得到以下结论:相比于线性模型，非线性模型与完全模型的运行安全性计算结果更为接近;在几项安全性指标中，轮重减载率与倾覆系数的相对误差较大，这是因为车体的偏载导致空气弹簧内部压强的变化，从而引起空气弹簧动态刚度的变化，而线性模型的刚度始终为定值;虽然线性模型相比于非线性模型计算误差稍大，但其与完全模型的计算误差仍在4%以内，这是由于二系悬挂特性的差异对轮轨作用力的影响相对较小。因此，用线性模型与非线性模型计算高速列车的运行安全性，可以满足工程要求。

图7 三种模型的车辆运行安全性指标Fig.7 The vehicle safety index of the three dynamic models of air spring

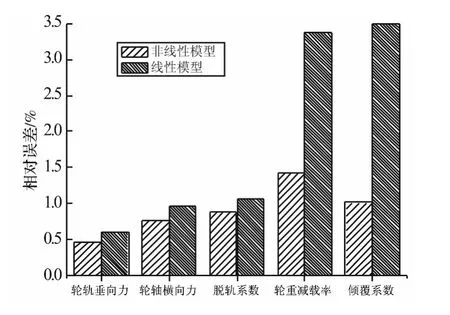
图8 非线性模型、线性模型与完全模型相比的相对误差Fig.8 The relative error of non-linear and linear models compared to complete model

3.2 车辆运行平稳性的计算

在直线工况下计算车辆的运行平稳性，轨道激励仍采用京津城际高铁轨道谱。平稳性计算结果主要包括车体横向、垂向加速度的最大值以及车体的垂向、横向平稳性。在车体前转向架中心地板面上设置加速度计，在计算结果中输出每步积分的加速度值。车体的平稳性按照下式计算:

式中W、A、f和F(f)的具体定义详见文献［13］。平稳性指标越小，说明车体的振动越小，标准中规定的1级平稳性指标应小于2.5。在不同速度下计算出的车辆各项平稳性指标如图9所示。

由车辆运行平稳性的计算结果可以得出以下结论:车体横向加速度与横向平稳性在三种模型下计算结果基本一致，这是由于三种模型均假设空气弹簧的垂向刚度与水平刚度没有耦合性;车体垂向加速度与垂向平稳性在三种模型下的计算结果误差较大，这是由于三种模型动态特性的差异对车体垂向振动的影响较大;对于车体垂向加速度与垂向平稳性，完全模型与非线性模型在250－350 km/h速度级之间具有非线性特性，而线性模型的指标随车速的变化基本呈线性变化。因此，在高速列车动力学中计算车体垂向平稳性，应用线性模型对空气弹簧进行建模会与实际情况产生较大的差异。

将三种空气弹簧动力学模型在整车模型下仿真的计算时间进行对比。整车仿真时间设定为40 s，积分步长设置为0.005 s，计算机CPU为2.93 GHz的双核奔腾处理器，三种模型在某一工况下的仿真时间对比如表1所示。由三种模型的计算耗时对比可知，线性模型的计算速度最快，非线性模型稍慢，而完全模型的计算时间是前两者的2.5倍左右。由此可知，在高速列车的动力学计算中，虽然完全模型的计算结果更为准确，但其计算速度较慢，且涉及的物理参量较多，不易确定;线性模型的计算速度较快，但不能体现空气弹簧的非线性特性;而非线性模型的计算速度和线性模型基本相同，且计算结果较为准确。因此，在高速列车的动力学计算中建议采用非线性模型对空气弹簧进行建模。

图9 三种模型的车辆运行平稳性指标性Fig.9 The vehicle ride comfort index of three dynamic models of air spring

表2 三种模型的仿真计算时间对比Tab.2 The simulation time of the three models

4 结论

首先建立了三种空气弹簧动力学模型的数学表达式，包括线性模型、非线性模型和完全模型。以车辆动力学的仿真结果对空气弹簧施加激励，对三种模型进行准静态仿真，研究了三种模型动态特性的差异。最后将三种模型引入高速动车组的整车动力学模型，并进行动力学仿真计算，以不同的空气弹簧建模方法对高速动车组进行了动力学特性分析。通过上述研究，主要可以得出以下结论:

(1)在准静态仿真中，非线性模型与完全模型的回滞曲线较接近，其二者回滞曲线两端较尖扁，体现了空气弹簧的非线性特性，而线性模型的回滞曲线呈椭圆形且阻尼特性较高;

(2)在整车动力学计算中，三种模型计算的车辆运行安全性指标差异不大，非线性模型与完全模型的相对误差在2%以内，线性模型与完全模型的相对误差在4%以内;

(3)三种模型对车辆的垂向平稳性指标影响较大，完全模型和非线性模型在250 km/h－300 km/h速度级间会呈现非线性特性，而线性模型的垂向平稳性指标呈线性变化;

(4)考虑到三种模型的计算速度，非线性模型与线性模型的计算速度相差不大，且比完全模型快2.5倍左右，因此在高速动车组的动力学工程计算中建议采用非线性模型。

［1］Oda N，Nishimura S.Vibration of air suspension bogie and their design［C］.Bull.JSME，1970，13(55):43 －50.

［2］Krettek O，Grajnert J.Die modelldarstellung pneumatischer fahrzeugfederungen und die vorauswahl der modellparameter［J］.ZEV+DET Glas.Ann，1991，115(5):142 －145.

［3］Nieto A J，Morales A L，Gonzalez A，et al.An analytical model of pneumatic suspensions［J］.Veh.Syst.Dyn，2007 45(6):505－524.

［4］Doquier N.Multiphysics modeling of multibody systemsapplication to railway pneumatic suspension［D］.Universite Catholique de Louvain，November，2010.

［5］Quaglia G，Sorli M.Air suspension dimensionless analysis and design procedure［J］.Veh.Syst.Dyn，2001，35(6):443－475.

［6］孔军.空气弹簧在我国轨道车辆中的应用与发展［J］.铁道车辆，2002:40(2):5－8.KONG Jun.Application and development of air springs for rail cars in our country［J］.Rolling Stock，2002:40(2):5－8.

［7］李芾，付茂海，黄运华.空气弹簧动力学特性参数分析［J］.西南交通大学学报，2003，38(3):276－281.LI Fu，FU Mao-hai，HUANG Yun-hua.Analysis of dynamic characteristic parameterofairspring［J］. Journalof Southwest Jiaotong University，2003，38(3):276－281.

［8］张广世，沈钢.带有连接管路的空气弹簧动力学模型研究［J］.铁道学报，2005，27(4):36－41.ZHANG Guang-shi，SHEN Gang.Study on dynamic airspring model with connecting pipe［J］.Journal of the China Railway Society，2005，27(4):36－41.

［9］张利国，张嘉钟，贾力萍等.空气弹簧的现状及其发展［J］.振动与冲击，2007，26(2):146－151.ZHANG Li-guo， ZHANG Jia-zhong， JIA Li-ping et al.Future and development of air springs［J］.Journal of Vibration and Shock，2007，26(2):146－151.

［10］王家胜，朱思洪.带附加气室空气弹簧动刚度的线性化模型研究［J］.振动与冲击，2009，28(2):72－76.WANG Jia-sheng， ZHU Si-hong. Linearizedmodelfor dynamic stiffness of air spring with auxiliary chamber［J］.Journal of Vibration and Shock，2009，28(2):72－76.

［11］李鹏，杨翊仁，鲁丽.气动力作用下高速车辆横向稳定性分析［J］.振动与冲击，2010，29(11):135－138.LI Peng，YANG Yi-ren，LU Li.Lateral stability of a highspeed train under aerodynamic force［J］.Journal of Vibration and Shock，2010，29(11):135－138.

［12］TB/T 2841—2005.中华人民共和国铁道行业标准，铁道车辆空气弹簧［S］，铁道部标准计量研究所，2005.

［13］中华人民共和国铁道部，高速动车组整车试验规范［S］.北京，2008.