Uniform asymptotics for finite-time ruin probability in somedependent compound risk models with constant interest rate

Yang Yang Liu Wei Lin Jinguan Zhang Yulin

(1School of Economics and Management, Southeast University, Nanjing 210096, China)(2School of Mathematics and Statistics, Nanjing Audit University, Nanjing 210029, China)(3College of Mathematics and System Science, Xinjiang University, Urumqi 830046, China)(4Department of Mathematics, Southeast University, Nanjing 210096, China)



Uniform asymptotics for finite-time ruin probability in somedependent compound risk models with constant interest rate

Yang Yang1,2Liu Wei3Lin Jinguan4Zhang Yulin1

(1School of Economics and Management, Southeast University, Nanjing 210096, China)(2School of Mathematics and Statistics, Nanjing Audit University, Nanjing 210029, China)(3College of Mathematics and System Science, Xinjiang University, Urumqi 830046, China)(4Department of Mathematics, Southeast University, Nanjing 210096, China)

Consider two dependent renewal risk models with constant interest rate. By using some methods in the risk theory, uniform asymptotics for finite-time ruin probability is derived in a non-compound risk model, where claim sizes are upper tail asymptotically independent random variables with dominatedly varying tails, claim inter-arrival times follow the widely lower orthant dependent structure, and the total amount of premiums is a nonnegative stochastic process. Based on the obtained result, using the method of analysis for the tail probability of random sums, a similar result in a more complex and reasonable compound risk model is also obtained, where individual claim sizes are specialized to be extended negatively dependent and accident inter-arrival times are still widely lower orthant dependent, and both the claim sizes and the claim number have dominatedly varying tails.

compound and non-compound risk models; finite-time ruin probability; dominatedly varying tail; uniform asymptotics; random sums; dependence structure

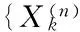
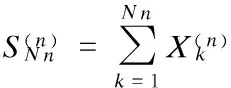
(1)

In the non-compound model, whereNk=1,k≥1, the finite-time ruin probability can be simplified as

(2)

This paper aims to investigate the asymptotics for the finite-time ruin probabilities in Eqs.(1) and (2) holding uniformly for alltsuch thatλ(t) is positive. Define the setΛ={t:λ(t)>0}.

1 Preliminaries

Hereafter, all the limit relationships hold forx→∞. For two positive bivariate functionsa(x,t) andb(x,t), we writea(x,t)b(x,t) (or, equivalently,b(x,t)≻a(x,t)) holds uniformly for alltin a nonempty setA, if lim sup supt∈Aa(x,t)/b(x,t)≤1; we writea(x,t)～b(x,t) holds uniformly for allt∈A, ifa(x,t)b(x,t) anda(x,t)≻b(x,t). For realy, the greatest integer smaller than or equal toyis denoted by [y].

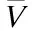
(3)

(4)

and they are said to be widely orthant dependent (WOD) if they are both WUOD and WLOD.

2 Uniform Asymptotics for Finite-Time Ruin Probabilities

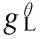
(5)

for someε0>0. Then for anyT∈Λ, it holds that uniformly for allt∈Λ∩[0,T],

(6)

Lemma 1 Under the conditions of Theorem 1, for allT∈Λ, it holds that uniformly fort∈Λ∩[0,T],

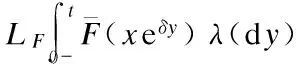
(7)

Proof The proof of Lemma 1 follows the line of Theorem 1.1 in Ref.[5].

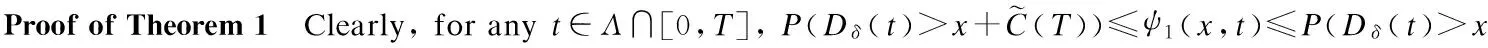
asε↓0, which implies that the desired lower bound in (6) holds. Again by Lemma 1, we obtain that uniformly for allt∈Λ∩[0,T],ψ1(x,t)≤P(Dδ(t)>x)

In the following, we study the uniform asymptotics for the finite-time ruin probability in a compound renewal risk model by the investigation of the asymptotic tail behavior of random sums. Some related results can be found in Refs.[6-8].

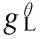
DenotethepartialsumbySn=X1+X2+…+Xn,n≥1.

Lemma 2 Let {Xn,n=1} be END nonnegative r.v.s with common distributionF∈Dand meanμF>0, andNbe an integer-valued r.v., independent of {Xn,n=1}, with distributionG∈Dand meanμG>0. Then

(8)

Proof For any 0<ε<1 and integerm, we divide the tail probability ofSNinto three parts:

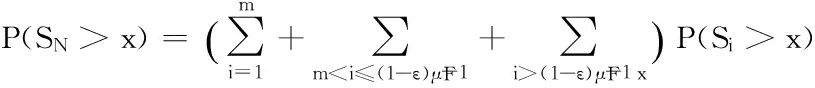
P(N=i)=:L1+L2+L3

(9)

ByF∈Dand Theorem 1 in Ref.[9], we have that

(10)

For anym

P(Si>x) =P(Si-iμF>x-iμF)≤

where the last step usesF∈DandCis a positive constant irrespective toi. By using Theorem 1 in Ref.[9] and the dominated convergence theorem, we obtain that

(11)

(12)

Thus, combining (9) to (12), we can obtain the upper bound in (8).

Now we estimate the lower bound ofP(SN>x). For any 0<ε<1 and integerm, we have that

L1+L4

(13)

ForL4, it holds that

Hence, by the strong law of the large numbers of END r.v.s[11]andF∈D, we obtain that

(14)

Therefore, (13), (10) and (14) yield the lower bound in (8).

(15)

which, byF∈DandG∈D, implies thatH∈D. So, by (1), Theorem 1 and (15), for any fixedT∈Λ, we obtain that

ψ(x,T)

(16)

(17)

holduniformlyforallt∈Λ∩[0,T]. Note that by (15), it holds that for anyy>1,

[1]Tang Q H, Su C, Jiang T, et al. Large deviations for heavy-tailed random sums in compound renewal model [J].StatistProbLett, 2001, 52(1): 91-100.

[2]Maulik K, Resnick S. Characterizations and examples of hidden regular variation [J].Extremes, 2004, 7(1): 31-67.

[3]Wang K Y, Wang Y B, Gao Q W. Uniform asymptotics for the finite-time ruin probability of a dependent risk model with a constant interest rate [J].MethodolComputApplProb, 2013, 15(1): 109-124.

[4]Liu L. Precise large deviations for dependent random variables with heavy tails [J].StatistProbLett, 2009, 79(9): 1290-1298.

[5]Tang Q H. Heavy tails of discounted aggregate claims in the continuous-time renewal model [J].JApplProb, 2007, 44(2): 285-294.

[6]Yang Y, Wang Y B, Leipus R, et al. Asymptotics for tail probability of total claim amount with negatively dependent claim sizes and its applications [J].LithMathJ, 2009, 49(3): 337-352.

[7]Yang Y, Lin J G, Huang C, et al. The finite-time ruin probability in two nonstandard renewal risk models with constant interest rate and dependent subexponential claims [J].JKoreanStatistSociety, 2012, 41(2): 213-224.

[8]Yang Y, Wang K Y, Liu J. Asymptotics and uniform asymptotics for finite-time and infinite-time absolute ruin probabilities in a dependent compound renewal risk model [J].JMathAnalAppl, 2013, 398(1): 352-361.

[9]Yi L, Chen Y, Su C. Approximation of the tail probability of randomly weighted sums of dependent random variables with dominated variation [J].JMathAnalAppl, 2011, 376(1): 365-372.

[10]Yang Y, Wang K Y. Precise large deviations for dependent random variables with applications to the compound renewal risk model [J].RockyMounJMath, 2013, 43(4): 1395-1414.

[11]Chen Y, Chen A, Ng K W. The strong law of large numbers for extend negatively dependent random variables [J].JApplProb, 2010, 47(4): 908-922.

带有常数利息率的相依复合风险模型中有限时破产概率的一致渐近性

杨 洋1,2刘 伟3林金官4张玉林1

(1东南大学经济管理学院,南京 210096) (2南京审计学院数学与统计学院,南京 210029) (3新疆大学数学与系统科学学院,乌鲁木齐 830046) (4东南大学数学系,南京 210096)

考虑了2个带有常数利息率的相依更新风险模型.首先研究了非复合风险模型,其中索赔额是上尾渐近独立且带有控制变换尾分布的非负随机变量,索赔时间间隔是宽下象限相依的,保费收入过程是一个非负的随机过程,利用风险理论中的方法,得到了有限时破产概率在某个有界区间上的一致渐近性.在此基础上,利用随机和尾渐近性的分析方法,进一步研究获得了更为复杂且合理的复合相依更新风险模型中有限时破产概率的一致渐近性公式,其中单个索赔额特殊化为广义负相依的,并且事故时间间隔仍然保持宽下象限相依的,索赔额和索赔次数均为控制变换尾的.

复合及非复合风险模型;有限时破产概率;控制变换尾;一致渐近性;随机和;相依结构

O211.4

s：The National Natural Science Foundation of China (No. 11001052, 11171065, 71171046), China Postdoctoral Science Foundation (No. 2012M520964), the Natural Science Foundation of Jiangsu Province (No. BK20131339), the Qing Lan Project of Jiangsu Province.

：Yang Yang, Liu Wei, Lin Jinguan, et al. Uniform asymptotics for finite-time ruin probability in some dependent compound risk models with constant interest rate[J].Journal of Southeast University (English Edition),2014,30(1):118-121.

10.3969/j.issn.1003-7985.2014.01.022

10.3969/j.issn.1003-7985.2014.01.022

Received 2013-08-29.

Biography：Yang Yang (1979—), male, doctor, associate professor, yyangmath@gmail.com.