结合环上的Jordan多重同态

李凌跃, 徐晓伟

(吉林大学 数学学院, 长春 130012)

(φ1*…*φn)(a1,…,an)=φ1(a1)…φn(an), (a1,…,an)∈R1×…×Rn.

结合环上的Jordan多重同态

李凌跃, 徐晓伟

(吉林大学 数学学院, 长春 130012)

通过引入Jordan多重同态、多重同态和布尔同态的概念, 利用布尔同态给出有1结合环上Jordan多重同态的结构, 并讨论一些特殊环上布尔同态的一般形式.结果表明, 有1结合环上Jordan多重同态即为多重同态.

Jordan多重同态; 多重同态; Jordan布尔同态; 布尔同态

0 引言与预备知识

结合环上导子和环同态是两类重要的映射.关于多重导子的研究目前已有很多结果, Brešar等证明了非交换素环上的双导子都是内的, 即给出了素环上双导子的结构[7]， 之后， 又给出了半素环上双导子的结构[8]; Jung等[9]研究了素环和半素环上满足恒等式的可换序3-导子; Park给出了素环和半素环上可换序4-导子类似的结果[10], 并讨论了素环和半素环上的可换序n-导子[11]; 徐晓伟等[12]利用Brešar半素环双导子的结构定理证明了半素环R上n-导子的像都在R的中心内; 王尧等[13]给出了一类特殊三角代数上n-导子的描述.

相对于Jordan同态和多重导子的研究, Jordan多重同态和多重同态的性质及结构的研究也有一定的理论意义.基于此, 本文通过引入Jordan多重同态、多重同态和布尔同态的概念, 利用布尔同态给出了有1结合环上Jordan多重同态的结构, 进而说明了有1结合环上Jordan多重同态就是多重同态.最后讨论了一些特殊环上布尔同态的一般形式.

设R1,…,Rn和S均为环, 映射f:R1×…×Rn→S, 对任意的i∈{1,2,…,n}及任意的(a1,…,an)∈R1×…×Rn,b∈Ri, 且:

1)f(a1,…,ai+b,…,an)=f(a1,…,ai,…,an)+f(a1,…,b,…,an);

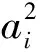
3)f(a1,…,aibai,…,an)=f(a1,…,ai,…,an)f(a1,…,b,…,an)f(a1,…,ai,…,an);

4)f(a1,…,aib,…,an)=f(a1,…,ai,…,an)f(a1,…,b,…,an).

若条件1)～3)成立, 则称f是R1×…×Rn到S的Jordann-重同态; 若条件1),4)成立, 则称f是R1×…×Rn到S的n-重同态.

结合环上的(Jordan)n-重同态可视为固定任意n-1个变量后, 关于余下的一个变量的(Jordan)同态.R1×R2到S的(Jordan)2-重同态也称为(Jordan)双同态.设Sn表示n阶对称群,R1=…=Rn=R, 如果对任意的σ∈Sn及任意的a1,…,an∈R, 有f(a1,…,an)=f(aσ(1),…,aσ(n)), 则称f是R×…×R到S的可换序(Jordan)n-重同态.可换序(Jordan)2-重同态也称为对称(Jordan)双同态.

下面总设R1,…,Rn,R和S为有1结合环, 且在无特殊说明情况下, 本文提到的环均为有1 结合环, 但环同态不要求把单位元映成单位元.Mn(R)和Tn(R)分别表示环R的全矩阵环和上三角矩阵环.eij是(i,j)分量为1、其余分量均为0的矩阵, 其行数、列数根据相应情形而定.[a,b]表示a和b的换位子, 即有[a,b]=ab-ba.F2表示2元域,为自然数集.Morita Context环是指所有如下形式矩阵构成的环其中:A,B为有1环；M为左A-右B-双模,N为左B-右A-双模,k1:M⊗N→A为双A-模同态,k2:N⊗M→B为双B-模同态.R中的矩阵按通常意义下的加法和如下定义的乘法构成环： 对任意的a,a′∈A,b,b′∈B,m,m′∈M,n,n′∈N, 有

有时k1(m⊗n)简记为mn,k2(n⊗m)简记为nm.

1 主要结果

引理1设f是R1×R2到S的Jordan双同态, 则对任意的a,b,c∈R1,x,y,z∈R2, 有:

1)f(a,x)=-f(a,x);

2)f([a,b],x)=f(a,[x,y])=0;

3)f(acb,x)=f(bca,x),f(a,xzy)=f(a,yzx);

4)f(a,x)=f(a,1)f(1,x), 且f(a,x)是幂等元;

5)f(a,x)f(b,y)=f(b,y)f(a,x).

证明: 1) 利用f(a+b,x2)的不同展开, 一方面,

f(a+b,x2)=f(a,x2)+f(b,x2);

另一方面,

从而

同理由f(a2,x+y)的不同展开知f(a,x)f(a,y)=-f(a,y)f(a,x), 再利用f((a+b)2,x)的不同展开, 一方面,

f((a+b)2,x)=f(a2,x)+f(b2,x)+f(ab+ba,x)；

另一方面, 由式(1)得

从而

在式(2)中取b=1, 有2f(a,x)=0.于是f(a,x)=-f(a,x).

2) 由1)和式(2)得

f([a,b],x)=f(ab-ba,x)=f(ab+ba,x)=0.

同理有f(a,[x,y])=0.

3) 利用f((a+b)c(a+b),x)的不同展开, 一方面,

另一方面, 由1)、式(1)及Jordan双同态的定义知

从而由1)知f(acb,x)=f(bca,x).同理利用f(a,(x+y)z(x+y))的不同展开, 有f(a,xzy)=f(a,yzx).

4) 由Jordan双同态的定义知f(a,1)=f(a,12)=f(a,1)2.从而f(a,1)是幂等元, 同理知f(1,a)是幂等元.此时由1)、式(1)及Jordan双同态的定义知

在式(4)中取a=a+b, 有f(a+b,x)=f(a+b,1)f(a+b,x).展开并用式(4)及1)得

在式(5)中取b=1, 并用式(3),(4)得

f(a,1)f(1,x)=f(1,1)f(a,x)=f(1,1)f(a,1)f(a,x)=f(a,1)f(a,x)=f(a,x).

同理有f(1,x)f(a,1)=f(a,x).此时

从而由f(a,1)和f(1,x)是幂等元及式(6)知f(a,x)是幂等元.

5) 由1)及式(1),(6)知

证毕.

为了刻画有1结合环上Jordan多重同态的结构, 下面引入Jordan布尔同态、布尔同态及*运算的概念.

定义1如果对任意的x∈R, 有φ(x)=φ(x)2, 则称(Jordan)同态φ:R→S为R到S的(Jordan)布尔同态.

定义2设映射φi:Ri→S(i=1,2,…,n), 定义映射φ1*…*φn:R1×…×Rn→S如下:

(φ1*…*φn)(a1,…,an)=φ1(a1)…φn(an), (a1,…,an)∈R1×…×Rn.

定义3设映射φi:Ri→S(i=1,2), 如果对任意的(a,b)∈R1×R2, 有φ1(a)φ2(b)=φ2(b)φ1(a).则称φ1,φ2是交换的, 如果对任意的(a,b)∈R1×R2, 有φ1(a)φ2(b)=φ2(b)φ1(a)=0, 则称φ1,φ2是正交的.

引理2结合环上Jordan布尔同态是布尔同态.

证明: 设φ是R到S的Jordan布尔同态, 则对任意的a,b∈R, 有

φ(a+b)=φ(a)+φ(b),φ(a2)=φ(a)2=φ(a),φ(aba)=φ(a)φ(b)φ(a).

此时

2φ(a)=(2φ(a))2=4φ(a)2=4φ(a),

从而2φ(a)=0, 即

φ(a)=-φ(a).(7)

又由于

从而由式(7)得

φ(a)φ(b)=φ(b)φ(a).(8)

对任意的c∈R, 利用φ((a+b)c(a+b))的不同展开, 一方面, 由式(7),(8)得

另一方面,

φ((a+b)c(a+b))=φ(aca+acb+bca+bcb)=φ(aca)+φ(acb)+φ(bca)+φ(bcb).

从而由式(7)知

φ(acb)=φ(bca).(9)

在式(9)中取b=ac并用式(8)得

φ(ac)=φ(ac)2=φ((ac)2)=φ(acca)=φ(a)φ(c2)φ(a)=φ(a)φ(c).

由Jordan布尔同态的定义, 显然有φ(a+c)=φ(a)+φ(c).于是φ是R到S的布尔同态.证毕.

下面给出Jordan双同态结构的刻画, 进而得到Jordan多重同态的结构.

定理1设f是R1×R2到S的映射, 则f是Jordan双同态当且仅当存在唯一的布尔同态φ:R1→S,ψ:R2→S, 使得f=φ*ψ, 并且φ与ψ交换,φ(1)=ψ(1).

证明: 必要性.先证存在性.对任意的(a,x)∈R1×R2, 令φ(a)=f(a,1),ψ(x)=f(1,x).则由引理1中4),5)及引理2知φ:R1→S与ψ:R2→S是交换的布尔同态, 且φ(1)=ψ(1).再由引理1中4)知, 对任意的(a,x)∈R1×R2, 有

f(a,x)=f(a,1)f(1,x)=φ(a)ψ(x)=(φ*ψ)(a,x).

下面证明唯一性.假设还有交换的布尔同态φ′和ψ′, 使得φ′(1)=ψ′(1)且f=φ′*ψ′, 则对任意的(a,x)∈R1×R2, 有(φ*ψ)(a,x)=(φ′*ψ′)(a,x).因而

故φ=φ′.同理有ψ=ψ′.

充分性.由于φ:R1→S与ψ:R2→S是交换的布尔同态, 从而对任意的a,b∈R1,x,y∈R2, 有

同理有

故由定义知φ*ψ是R1×R2到S的Jordan双同态.证毕.

注1定理1中条件φ(1)=ψ(1)是必要的, 即φ(1)≠ψ(1)时,f分解不唯一.

例1设环R=S=F2×F2, 对任意的(a,b)∈R, 定义φ(a,b)=(0,b),ψ(a,b)=(b,b).易见φ和ψ是交换的布尔同态, 且φ(1,1)≠ψ(1,1),φ*ψ=ψ*φ.令f=φ*ψ, 则由定理1知f为Jordan双同态, 但f分解不唯一.

推论1若f是R×R到S的映射, 则f是对称Jordan双同态当且仅当存在唯一的布尔同态φ:R→S, 使得f=φ*φ.

证明: 必要性.由定理1知, 存在唯一的布尔同态φ和ψ, 使得f=φ*ψ, 并且φ与ψ交换,φ(1)=ψ(1).由于f对称, 故φ*ψ=ψ*φ.再由定理1中φ和ψ的唯一性知φ=ψ.最后由定理1中φ,ψ的唯一性知, 使得f=φ*φ的φ是唯一的.

充分性.由定理1知φ*φ显然是对称Jordan双同态.

推论2设f是R1×…×Rn到S的映射, 则f是Jordann-重同态当且仅当存在唯一的布尔同态φi:Ri→S,i∈{1,2,…,n}, 使得f=φ1*…*φn, 并且φ1,…,φn两两交换,φ1(1)=…=φn(1).进一步, 当R1=…=Rn时,f是可换序的当且仅当φ1=…=φn.

证明: 必要性.先证存在性.固定Jordann-重同态f:R1×…×Rn→S的后n-2个变量, 可以将其视为Jordan双同态k:R1×R2→S, 这里k(x1,x2)=f(x1,x2,a3，…,an), 其中: (a3,…,an)∈R3×…×Rn给定; (x1,x2)∈R1×R2任意.从而由引理1中4)知f(a1,…,an)是幂等元, 即有

此外, 对任意的(a1,…,an),(b1,…,bn)∈R1×…×Rn, 当(a1-b1,…,an-bn)中非零分量的个数≤2时,f(a1,…,an)和f(b1,…,bn)可视为同一个Jordan双同态的两个像.从而由引理1中4),5)知f(a1,…,an)与f(b1,…,bn)交换, 且有

下面用归纳法证明Jordann-重同态f满足

f(a1,…,an)=f(a1,1,…,1)…f(1,…,1,an),

其中(a1,…,an)∈R1×…×Rn.当n=2时, 由定理1的证明知结论成立.当n>2时, 假设结论对Jordan (n-1)-重同态成立, 即对Jordan (n-1)-重同态g:R1×…×Rn-1→S, 有

g(a1,…,an-1)=g(a1,1,…,1)…g(1,…,1,an-1), (a1,…,an-1)∈R1×…×Rn-1.

对Jordann-重同态f, 用an固定最后一个变量, 则f关于前n-1个变量可视为R1×…×Rn-1到S的Jordan (n-1)-重同态, 即有Jordan (n-1)-重同态h:R1×…×Rn-1→S, 使得h(a1,…,an-1)=f(a1,…,an-1,an).此时由归纳假设及式(10),(11)知

令φi(ai)=f(1,…,1,ai,1,…,1),i∈{1,2,…,n}, 则由引理2知φi分别是Ri到S的同态,φ1(1)=…=φn(1), 且φi是两两交换的幂等元, 且由式(12)知f(a1,…,an)=φ1(a1)…φn(an).

充分性.由Jordann-重同态的定义自然有f=φ1*…*φn是Jordann-重同态.进一步,φ1=…=φn时f是可换序Jordann-重同态.

结合环上Jordan同态与同态、反同态关系密切.下面考虑Jordan多重同态与多重同态、多重反同态的关系.一方面, 由定义易知多重同态和多重反同态是Jordan多重同态; 另一方面, 若有n个布尔同态φi:Ri→S,i∈{1,2,…,n}, 使得f=φ1*…*φn, 并且φ1,…,φn两两交换,φ1(1)=…=φn(1), 则f是n-重同态, 也是n-重反同态.于是由定理1知, Jordann-重同态即为n-重同态, 也为n-重反同态, 从而有如下推论.

推论3设f是R1×…×Rn到S的映射, 则f是Jordann-重同态当且仅当f是n-重同态, 当且仅当f是n-重反同态.

引理3设φ:R→S是布尔同态,E是由R中换位子和幂零元生成的理想, 则φ限制在E上为零.

证明: 设K为φ的核, 由同态基本定理知R/K≅φ(R).由于φ是布尔同态, 从而φ(R)中幂零元和换位子只能为零, 故R的幂零元和换位子均在K中, 即E⊆K, 从而φ限制在E上为零.证毕.

由于全矩阵环和列有限矩阵环都可以由换位子生成, 从而有:

例2设n≥2, 则Mn(R)到S的布尔同态必为零.

例3列有限矩阵环CFM(R)到S的布尔同态必为零.

证明: 设φ为列有限矩阵环CFM(R)到S的布尔同态, 由引理3知, 对任意的i,j,k∈, 有

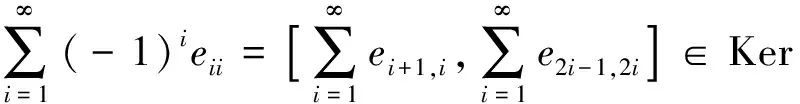
进而有

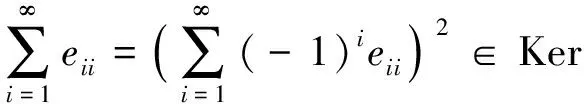
从而有CFM(R)=Kerφ, 即φ(CFM(R))=0.

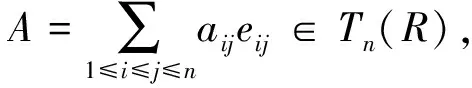
Φ(A)=φ1(a11)+…+φn(ann).

φi(ai)φj(aj)=Φ(aieii)Φ(ajejj)=Φ((aieii)(ajejj))=0.

从而φ1,…,φn是R到S的两两正交的布尔同态, 且

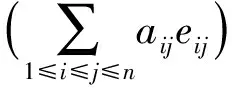
充分性.由Φ(A)=φ1(a11)+…+φn(ann)和φ1,…,φn的正交性知Φ(A)是环同态, 且

Φ(A)2=(φ1(a11)+…+φn(ann))2=φ1(a11)+…+φn(ann)=Φ(A).

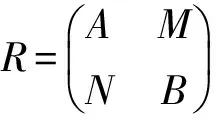
φ(a)ψ(b)=Φ(ae11)Φ(be22)=Φ((ae11)(be22))=0.

同理ψ(b)φ(a)=0.从而φ,ψ是正交的布尔同态.又

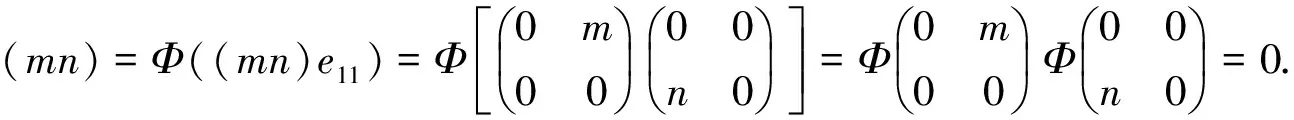
同理有ψ(nm)=0, 且

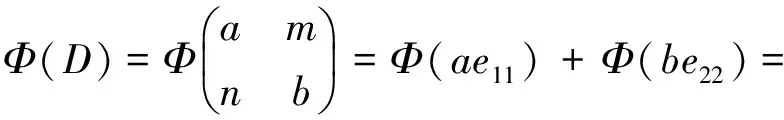
充分性.由Φ(D)=φ(a)+ψ(b)和φ,ψ的正交性知Φ(D)是环同态, 且

Φ(D)2=(φ(a)+ψ(b))2=φ(a)+ψ(b)=Φ(D).

[1]Jacobson N, Rickart C E.Jordan Homomorphisms of Rings [J].Trans Amer Math Soc, 1950, 69: 479-502.

[2]Herstein I N.Jordan Homomorphisms [J].Trans Amer Math Soc, 1956, 81: 331-341.

[3]Smiley M F.Jordan Homomorphisms onto Prime Rings [J].Trans Amer Math Soc, 1957, 84: 426-429.

[5]Brešar M.Jordan Homomorphisms Revisited [J].Math Proc Cambridge Philos Soc, 2008, 144(2): 317-328.

[6]WANG Yao, WANG Yu.Jordan Homomorphisms of Upper Triangular Matrix Rings [J].Linear Algebra Appl, 2013, 439(12): 4063-4069.

[7]Brešar M, Martindale W S, Miers C R.Centralizing Maps in Prime Rings with Involution [J].J Algebra, 1993, 161(2): 342-357.

[8]Bresšar M.On Certain Pairs of Functions of Semiprime Rings [J].Proc Amer Math Soc, 1994, 120(3): 709-713.

[9]Jung Y S, Park K H.On Prime and Semiprime Rings with Permuting 3-Derivations [J].Bull Korean Math Soc, 2007, 44(4): 789-794.

[10]Park K H.On 4-Permuting 4-Derivations in Prime and Semiprime Rings [J].J Korean Soc Math Educ Ser B: Pure Appl Math, 2007, 14(4): 271-278.

[11]Park K H.On Prime and Semiprime Rings with Symmetricn-Derivations [J].Journal of the Chungcheong Mathematical Society, 2009, 22(3): 451-458.

[12]XU Xiaowei, LIU Yang, ZHANG Wei.Skewn-Derivations on Semiprime Rings [J].Bull Korean Math Soc, 2013, 50(6): 1863-1871.

[13]WANG Yao, WANG Yu, DU Yiqiu.n-Derivations of Triangular Algebras [J].Linear Algebra Appl, 2013, 439(2): 463-471.

JordanMulti-homomorphismsonAssociativeRings

LI Lingyue, XU Xiaowei
(CollegeofMathematics,JilinUniversity,Changchun130012,China)

We introduced the notions of Jordan multi-homomorphisms, multi-homomorphisms and Boolean homomorphism.Using Boolean homomorphisms, we described the structures of Jordan multi-homomorphisms on associative rings with identity, and then showed that a Jordan multi-homomorphism is a multi-homomorphism on associative rings with identity, and finally, gave general forms of Boolean homomorphisms on some special rings.

Jordan multi-homomorphism; multi-homomorphism; Jordan Boolean homomorphism; Boolean homomorphism

2014-03-14.

李凌跃(1989—), 女, 汉族, 硕士研究生, 从事环论的研究, E-mail: lingyue.li@gmail.com.通信作者: 徐晓伟(1978—), 男, 汉族, 博士, 副教授, 从事环论的研究, E-mail: xuxw@jlu.edu.cn.

国家自然科学基金(批准号： 11371165; 11101175).

O153.3

A

1671-5489(2014)06-1105-07

10.13413/j.cnki.jdxblxb.2014.06.01

赵立芹)