光栅衍射中谱线缺级现象及其仿真*

叶伏秋，彭善琼

(1.吉首大学物理与机电工程学院，湖南 吉首 416000；2.湖南第一师范学院，湖南 长沙 410205)

光栅衍射中谱线缺级现象及其仿真*

叶伏秋1，彭善琼2

(1.吉首大学物理与机电工程学院，湖南 吉首 416000；2.湖南第一师范学院，湖南 长沙 410205)

理论推导了入射光以不同角度入射时的谱线缺级现象产生机理和被观察到的条件，数值模拟方法验证了垂直入射下的谱线缺级现象产生的条件，比较了入射光以不同角度入射时的谱线缺级现象.实验结果表明，垂直入射与斜入射时谱线缺级条纹均满足j=kd/b，其区别在于相同实验条件下能观察到的缺级条纹的范围存在一定的差异.

光栅衍射；谱线缺级；缺级条件

一束平行光经光栅衍射后在光屏上会产生一定的衍射图样，衍射图样的光强分布可以理解为单缝衍射因子与缝间干涉因子的乘积，衍射的实质可理解为多光束干涉受到单缝衍射调制的结果.根据光栅衍射的相关理论可知，衍射图样中本该出现光谱线的地方却未出现光谱线，即谱线缺级现象.国内现行教材涉及到了谱线缺级现象[1-2]，光栅衍射实验在大学物理实验中也占有相当重要的地位.然而，大部分的研究仅停留在光线垂直于光栅平面入射下的谱线缺级现象，而对于光线斜入射下的谱线缺级现象的研究较为少见，而且很多文献仅立足于d/b的值为整数的情况下，对于d/b的值不为整数时是否出现缺级现象并未说明.

笔者从理论上推导光束垂直于光栅平面入射时与斜入射时谱线缺级现象和观察到的条件，并运用Matlab模拟验证了光栅衍射中的谱线缺级现象产生的条件.

1 不同入射方向下的谱线缺级现象产生条件的理论推导

在光栅每个缝的衍射不形成暗纹的条件下，才能形成光栅衍射明纹.若光栅某级明纹对应的衍射角θ同时满足单缝衍射的暗纹条件，则这一级明纹不会出现，由此产生了缺级现象[3].

1.1垂直入射下谱线缺级现象

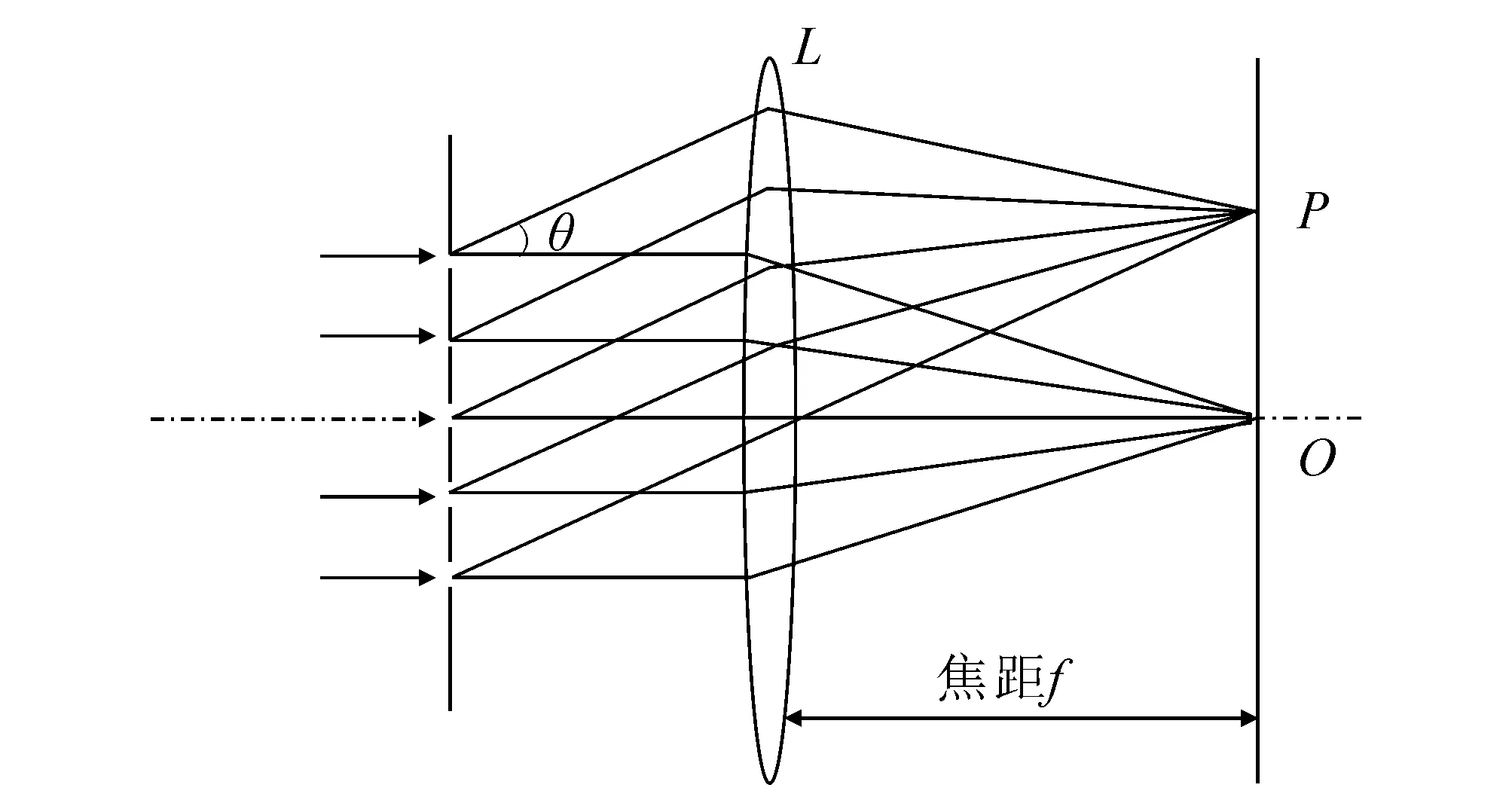
图1 垂直入射下的光栅衍射

一束平行光直接投射到光栅平面上，在光栅后面放置一透镜L，那么在透镜L的焦平面上放置的屏幕上将产生明暗相间的衍射图样，如图1所示.光栅的衍射条纹可以看作是单缝衍射与多缝干涉的综合结果.

在单缝衍射中，设入射光波长为λ，且垂直于缝的平面入射，波面和缝面重合.光束的初相位为0°，振幅为A0，缝B′B宽为b，如图2所示.

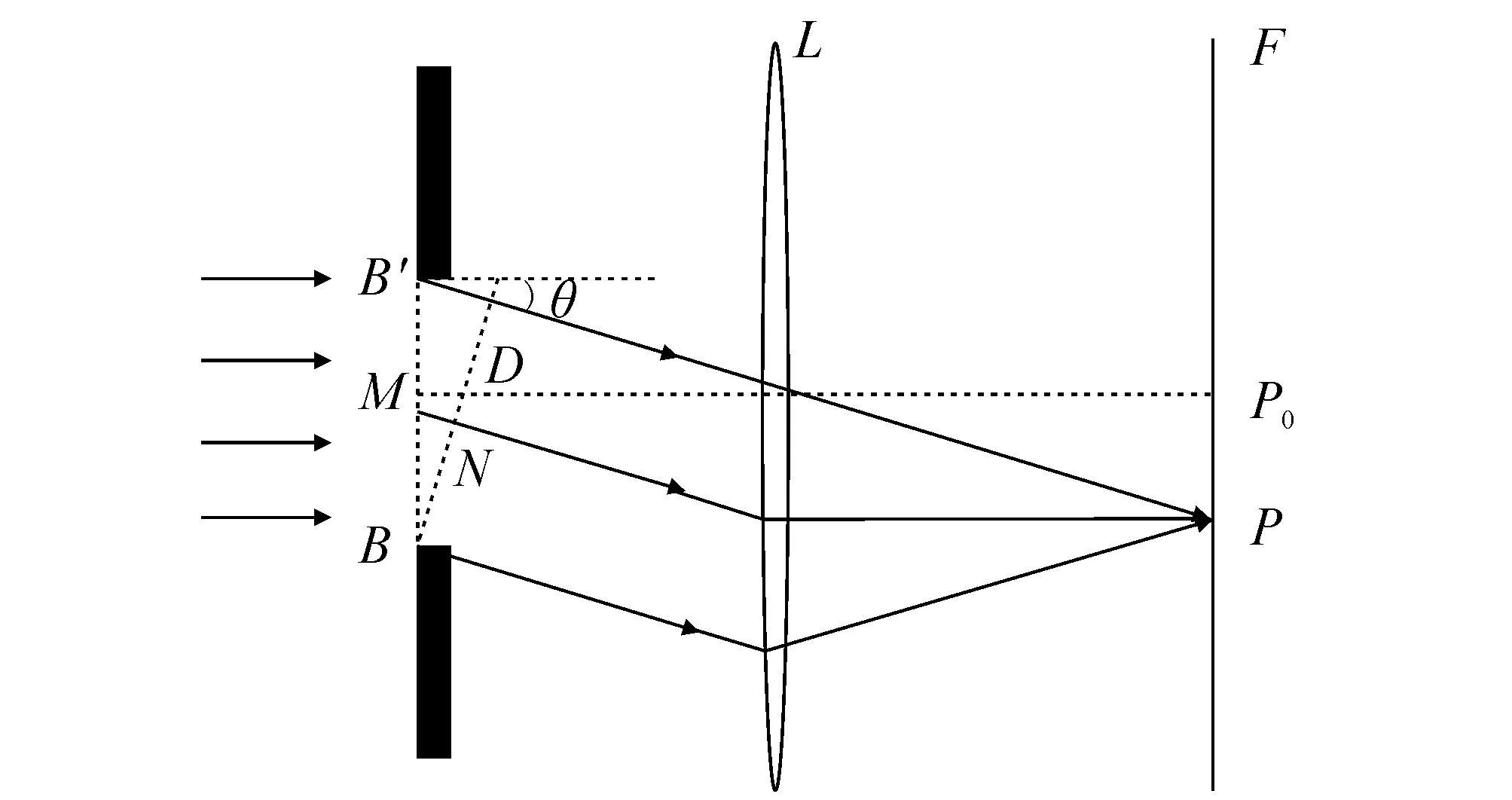
图2 垂直入射时的单缝衍射

现将单缝分为一组平行于缝长的窄带(带宽为dx)，据惠更斯-菲涅尔原理，狭缝处各窄带发出的次波的振动为

根据菲涅尔积分可知，平面BD上N点的光振动的表达式为

(1)

将(1)式积分(从x=0到x=b)，可得衍射角θ的所有次波在观察点P叠加起来的合振幅为

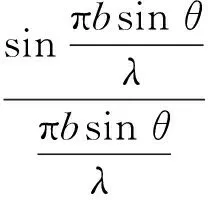
(2)

当光屏放在透镜L的焦平面上时，光屏上将出现衍射图样.因为光强正比于振幅的平方，所以光强的分布为公式(3)，且不同的衍射角θ对应于光屏上不同的观察点.由(2)式可知，当sin(πbsinθ/λ)=0且πbsinθ/λ≠0时，则IP=0，即此时观察点光强为0，屏上这些点是暗的[4].垂直入射时的单缝衍射光强最小值位置满足：

bsinθ=kλk=±1,±2，….

(3)

对于多光束干涉，设有N束频率相同的光沿着同一直线振动，且各相邻光束之间有相同的相位差φ和振幅A0，其叠加的结果用A0ei(ωt+φ0)来表示，则

Aeiφ0=A0[1+eiφ+…+ei(N-1)φ].

(4)

据等比数列的求和公式，有

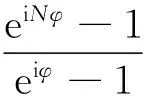
(5)

由于光的强度正比于振幅的平方，所以叠加后的光强为

I=A2=Aeiφ0Ae-iφ0.

(6)

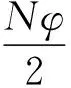
(7)

其中j0=Nj处为极大值[5].若j0=0,N,2N,…，其中N为整数倍，(7)式可整理得到相同位差的多光束叠加光强最大值位置满足

φ=2jπ.

(8)

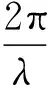
dsinθ=jλj=0,±1,±2,….

(9)

由(3)，(9)式可得

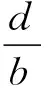
(10)

由上述推导可知，入射光垂直于光栅平面入射时，光谱条纹中满足(10)式的级数缺失，所缺级的级次由光栅常数和缝宽决定.

据(9)式和三角函数的有界性可知-d≤jλ≤d，即

(11)

当光栅光谱的第j级条纹同时满足(10)，(11)式时，该级谱线缺级现象才会被观察到.

1.2斜入射下的谱线缺级现象

图3 斜入射下的光栅衍射

在实际应用中，入射光相对于光栅平面的法线夹角不等于90°.如图3所示，平行光以一定的入射角射向平面衍射光栅，光束中通过光栅的部分经透镜L在光屏上出现衍射图样.

根据衍射理论，当一束平行光斜入射到光栅的表面时，不同缝间光发生干涉，同时每条缝发生衍射[6-7].

设入射光分居光栅法线的两侧，并与光栅法线的夹角为α(α>0)时，(1)式变为

(12)

b(sinθ±sinα)=kλk=±1,±2,…，

(13)

其中平行光与衍射光在法线同侧时取加号，异侧时取减号.

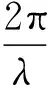
d(sinθ±sinα)=jλj=0,±1,±2,…，

(14)

由(13)，(14)式可得，斜入射下的缺级现象产生的条件同样是(10)式.

当入射光从光栅法线上方入射时，根据(14)式可知，能观察到谱线级数范围为

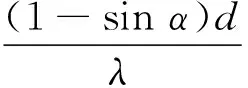
(15)

当入射光从光栅法线下方入射时，根据斜入射下的光栅方程可知，此时能观察到谱线级数范围为

(16)

故在斜入射条件下，当入射光从光栅法线上方入射时，同时满足(10)，(15)式时，缺级现象才能被观察到；当入射光从光栅法线下方入射时，同时满足(10)，(16)式时，缺级现象才能被观察到.

1.3垂直入射与斜入射下的谱线缺级现象的区别

由上述理论的推导可知，光线无论如何入射，其缺级现象产生的充分条件是一样的，即如果所缺级条纹级数都存在，则所缺级数是固定不变的.

比较(11)，(15)，(16)式可知，垂直入射时光栅衍射图样中所缺谱线级数范围与斜入射时谱线缺级级数范围是不一样的，能观察到缺级条纹数目一般情况下也是不一样.

若某光栅衍射实验满足条件d=2b时，取d=2 μm，λ=500 nm，N=6，A0=1，实验观察的谱线级数和缺级现象见表1.

表1 不同入射角下观察到的谱线缺级现象

注 “☆”表示该级谱线能观察到且缺级，“★”表示该级谱线能观察到且不缺级.

由表1可知，垂直入射与斜入射时能观察到的谱线缺级的范围是不一样的，当入射角发生变化时，谱线缺级现象的范围也随之发生变化.

2 基于MATLAB的实验分析

在图2中，设入射光的振幅为A0，波长为λ，初相为0，观察点P所对应的衍射角为θ，光栅衍射的光强是单缝衍射因子和缝间干涉因子的乘积[8].据(2)式可知，单缝衍射因子为

(17)

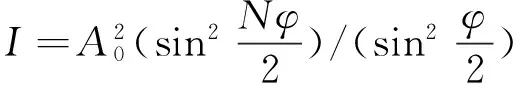
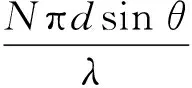
(18)

由(17)，(18)式可知，入射光经光栅衍射后的光强为

为了验证满足相关条件是否产生缺级现象，构造光强关于条纹级数j的函数[9]，将光栅方程dsinθ=jλ代入(12)式可得

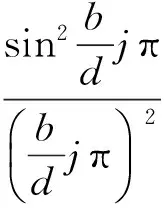
(19)

设d=3b，取d=5 μm，λ=500 nm，N=6，A0=1.由(10)式可以预测，该组条件下的光栅光谱的j级条纹对应的光强为0，其中j=±3k(k=1,2,3,…,n).即这些级数缺失.

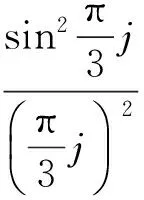
当d=4b/3时，取d=5 μm，λ=500 nm，N=6，A0=1.根据理论推导的结论(10)式可以预测，该组条件下的光栅光谱的±4k级条纹对于的光强为0，即这些级数缺失，其中k=1，2，3，…，N.

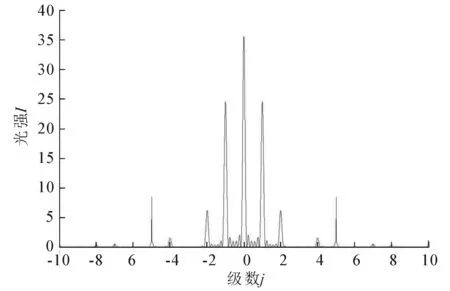
图4 d=3bj时光强与级数关系

图5 d=4b/3时光强与级数关系

由图5可知，j=±4k处的光强都等于0，k=1，2，3，…，N，即在这些地方出现了缺级现象，与理论预测一致.

由图4，5可知，无论d/b的值是否为整数，只要谱线级数满足(10)式，则对应的谱线缺失[10].

3 结语

对于一定的波长来说，光栅衍射各级谱线的强度都有固定的分布.光栅衍射的光强是单缝衍射和缝间干涉2个因子的乘积.当光栅衍射的衍射角θ既满足单缝衍射极小值条件，又满足多缝干涉主极大的条件时，衍射角θ所对应的衍射主极大条纹消失，即出现谱线缺级现象.理论推导表明无论是光线垂直入射还是斜入射，谱线产生缺级的级次都须满足j=kb/h这个条件.而在垂直入射下出现的谱线缺级的范围与斜入射下出现谱线缺级的范围是不一样的，且当改变入射角时，出现谱线缺级现象的范围也是不一样的.

[1] 姚启钧.光学教程[M].北京：高等教育出版社，2008：92-103.

[2] 母国光，战元龄.光学[M].北京：高等教育出版社，2009：237-254.

[3] 杨 坤.试论光栅缺级现象[J].洛阳师专学报，1998，18(2)：42-44.

[4] 赵晓春.光的单缝衍射与光的双缝干涉的本质初探[J].物理教师，2013，34(2)：58-63.

[5] 贺德春，韩振海.多光束干涉的研究[J].河西学院学报，2006，22(2)：42-44.

[6] 徐翠艳，王 辉.关于光栅斜入射问题的分析[J].渤海大学学报：自然科学版，2009，30(4)：359-361.

[7] 彭程远，李本喜，杨 鑫.对光线斜入射时光栅衍射的讨论[J].阜新矿业学院学报：自然科学版，1995，14(3)：115-117.

[8] 赵 纯，范素芹.夫琅和费光栅衍射光强分析[J].广西物理，2010，31(1)：40-42.

[9] 张景川.基于MATLAB的光栅衍射条纹强度研究[J].甘肃联合大学学报：自然科学版，2011，25(1)：52-55.

[10] 卢 勇.光栅衍射中d/b是否整数对缺级的影响[J].台州师专学报，2001，23(6)：43-46.

(责任编辑 向阳洁)

SpectralLineAbsenceaboutGratingDiffraction

YE Fuqiu

(College of Physics,Mechanical and Electrical Engineering,Jishou University,Jishou 416000,Hunan China)

with incident light of different angles,the conditions for the phenomenon of spectral line absence occuring and being observed are theoretically deducted.By the means of numerical simulation,the condition for the phenomenon of spectral line absence under the vertical incidence is verified.And with incident light of with different angles the spectral line absence is compared.The results show that the phenomenon meetsj=kd/b.The difference between the two incidences is that the observed range of the spectral line’s absence striation is different to some extent under the same experimental conditions.

grating diffraction;spectral line absence;conditions for absence

1007-2985(2014)03-0044-05

2014-02-25

湖南省自然科学基金资助项目(11JJ6002；11JJ6060)，湖南省教育厅科学研究项目(10A100，12C0314)

叶伏秋(1967-)，男，湖南吉首人，吉首大学物理与机电工程学院副教授，硕士，主要从事光学及信息光学研究.

O436

A

10.3969/j.issn.1007-2985.2014.03.010