测井标准井节箍深度值的确定新方法
2014-09-06任中豪张文昌朱新民晋新伟田文涛
任中豪, 张文昌, 朱新民, 晋新伟, 田文涛
(1.中国石油冀东油田分公司工程监督中心,河北唐海 063200;2.中国石油冀东油田分公司开发处,河北唐山 036004)
测井深度标准井是用于刻度或检验测井深度系统的标准井[1],其节箍深度的精准度是标准井能否使用的重要指标。目前,对新建标准井B的深度量值传递,是选取某一深度标准井A,将标准井A的深度量值传递到新建标准井B[2-3],其传递精度取决于深度标准井A的节箍深度精度和测井队深度系统标定精度,可信度较低。冀东油田测井深度标准井柳X井的深度量值由中原油田卫古2井传递,在使用中发现原始标准节箍深度误差较大,影响了标准井的使用效果。
为提高柳X井的深度量值精度,笔者利用多个测井队将深度系统分别经不同的深度标准井刻度合格后、传递到柳X井的节箍深度数据集,采用加权平均法求取节箍深度的最佳估计值,即利用多口深度标准井对柳X井进行深度量值传递,提高了新建标准井节箍深度值的精度和可信度。
1 最佳估计值的计算思路
在同一测量条件下、同一测量人使用同一测量工具、采用同样测量方法测量多次,即等精度测量多次时,其最佳估计值就是多次测量值的平均值,且平均值服从正态分布。当测量次数趋于无穷大时,平均值也收敛于该测量工具精度下的最佳值,但其前提条件是等精度测量,且测量结果的精度受测量工具精度的制约。
利用某测井深度标准井A,对新建标准井B进行深度量值传递,其传递精度取决于深度标准井A的节箍深度精度和测井队深度系统标定精度,可信度较低。所以,利用多次电缆深度系统检验测量值,来求取标准井节箍深度的最佳估计值。多次测量值分别由不同的服务商测井小队所测,其电缆深度系统的刻度方式和标定井均不相同,深度系统丈量方式有磁记号和马丁代克2种方式[4-7], 操作工程师也非同一人,因此多次测量为不等精度测量,其测量值可信度不等,且为有限次数,无法使用等精度平均法求取其最佳估计值。如果能用一个权值来表示这多次不等精度测量值的不同可信度,就可以利用加权法来体现不同精度测量值在求取最佳估计值中的贡献[8-12]。
2 利用加权法求取最佳估计值的计算方法
计算单次不等精度电缆测量值的权值时,需要一个反映单次电缆测量值离散程度的参数,定义为误差度。标准差可以反映一个多次等精度测量数据集x1,x2,…,xM的离散程度,其计算公式[13]为:
(1)
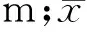
标准差评价的数据集是针对一个被测量物的测量值,单次电缆测量并未完成对单个节箍多次等精度测量,但单次电缆测量完成了对下井多根套管长度的等精度测量,每根套管在地面都进行了测量,且多数套管为同一规格,其长度相同,那么单次电缆测量得到的多根套管长度值就等同于一个多次等精度测量数据集,可利用这个数据集计算单次电缆测量的误差度σ。
假设单次电缆测量所测N根套管的长度为x1,x2,…,xN,而套管的地面测量值为y1,y2,…,yN(实际y1,y2,…,yN多数相等),那么单次电缆测井误差度的计算公式为:
(2)
式中:σ为误差度,m;xi为第i根套管的电缆测量值,m;yi为第i根套管的地面测量值,m。
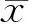
(3)
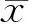
其中x1、x2相互独立,则根据误差合成公式:
(4)
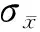
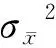
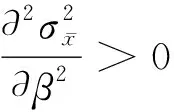
(5)
将式(4)带入一阶导数式,可以得到:
(6)
整理式(6),可以得到:
(7)
则标准节箍的最佳估计值计算公式为:
(8)
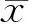
用归纳法推广到一般情况,设x1、x2、…,xN为N个不等精度独立测量值,其对应误差为σ1、σ2、…,σN。同样,可以得到类似的结果:
3 柳X井标准节箍深度最佳估计值的计算
柳X井深3 993 m,最大井斜角3°,每隔500 m选一个节箍作为标准节箍,共有7个节箍。柳X井原始标准节箍深度值由中原油田深度标准井卫古2井进行深度量值传递(见表1)。
表1卫古2井传递的原始标准接箍深度值
Table1DepthvalueoforiginalstandardcollartransferredbyWellWeigu2
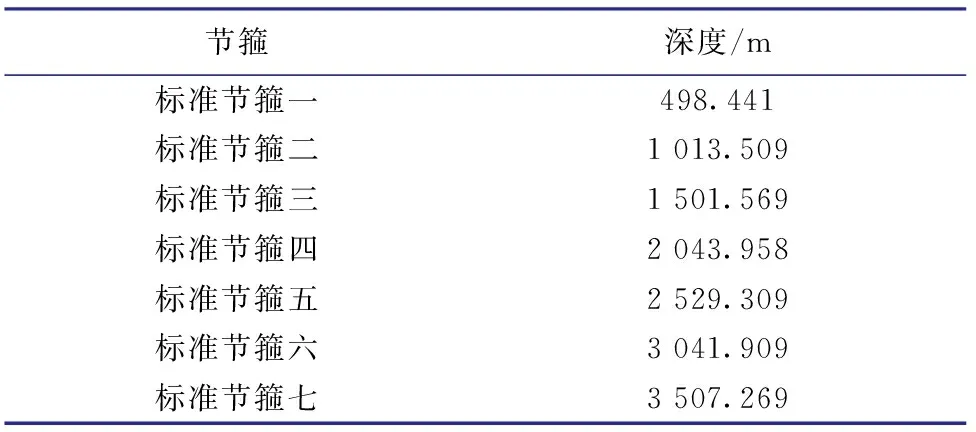
节箍深度/m标准节箍一498.441标准节箍二1 013.509标准节箍三1 501.569标准节箍四2 043.958标准节箍五2 529.309标准节箍六3 041.909标准节箍七3 507.269
各服务商测井队在柳X井进行的15次测量数据如表2所示,测井队深度系统分别标定于长城、中油、渤钻、大庆、中原、胜利等6家深度标准井。为避免各测井队测量数据的零点不统一,各测井队统一以井口法兰盘面作为深度参考点(即深度0 m点),所记录标准节箍深度值均为对零偏移后的数据。
根据式(2)计算电缆测量误差度时,xi=Li+1-Li,yi=li+1-li。其中,Li+1和Li分别为电缆测量i+1节箍长度和电缆测量i节箍长度,m;li+1和li分别为地面测量i+1节箍长度和地面测量i节箍长度,m。
计算时,选择同批次相同规格的单根套管为最佳计算单元,由于节箍数据很多,选择了7个标准节箍深度值作为计算单元。根据各服务商测井队在柳X井所测标准节箍深度值(见表2)和地面测量累计所得标准接箍深度值(见表3),利用式(2)计算得到15次电缆校验测井的误差度(见表4)。
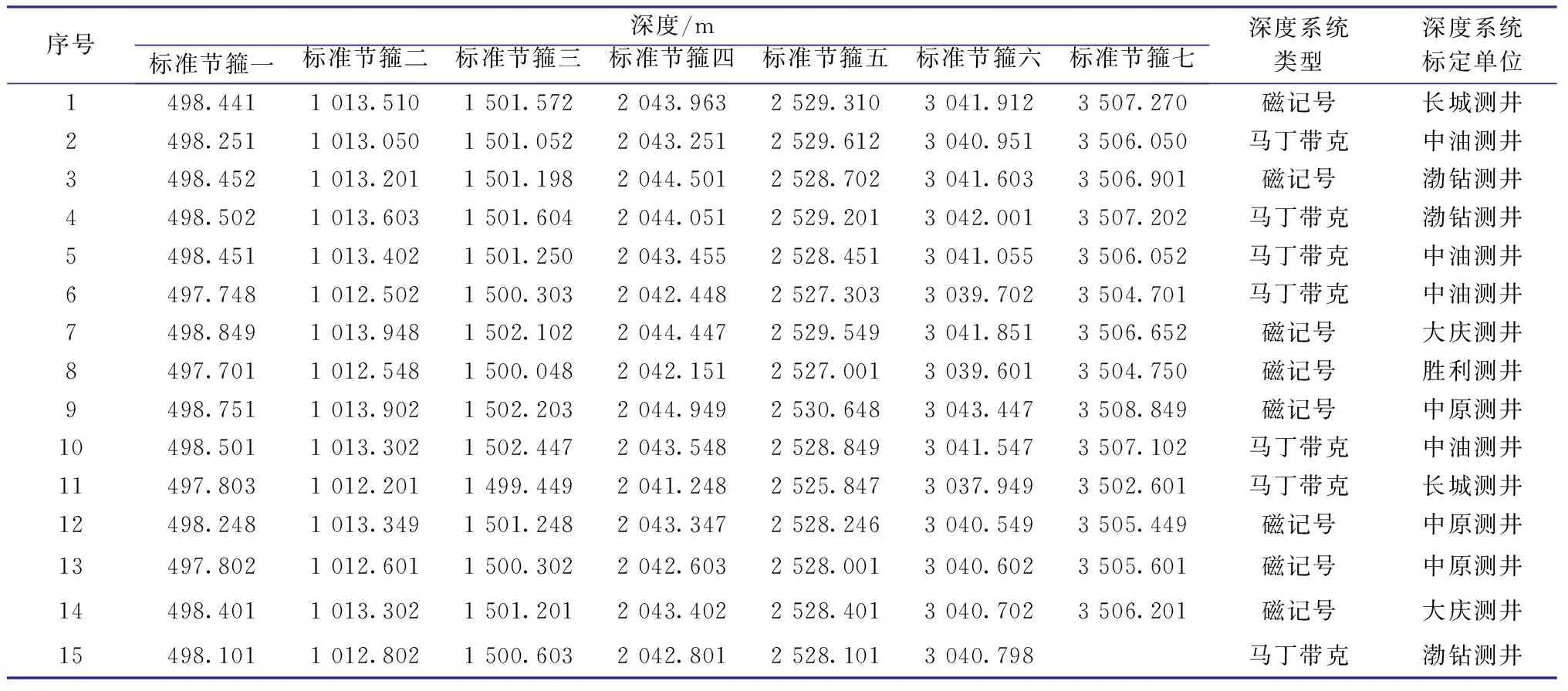
表2 各服务商测井队在柳X井所测标准节箍深度值
表3地面测量累计所得标准接箍深度
Table3Standardcollardepthvaluemeasuredintheground
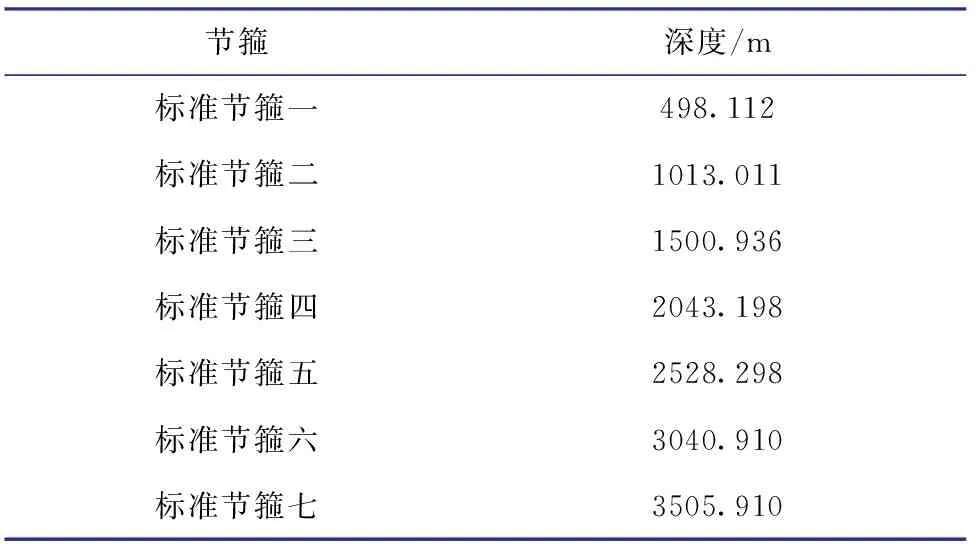
节箍深度/m标准节箍一498.112标准节箍二1013.011标准节箍三1500.936标准节箍四2043.198标准节箍五2528.298标准节箍六3040.910标准节箍七3505.910
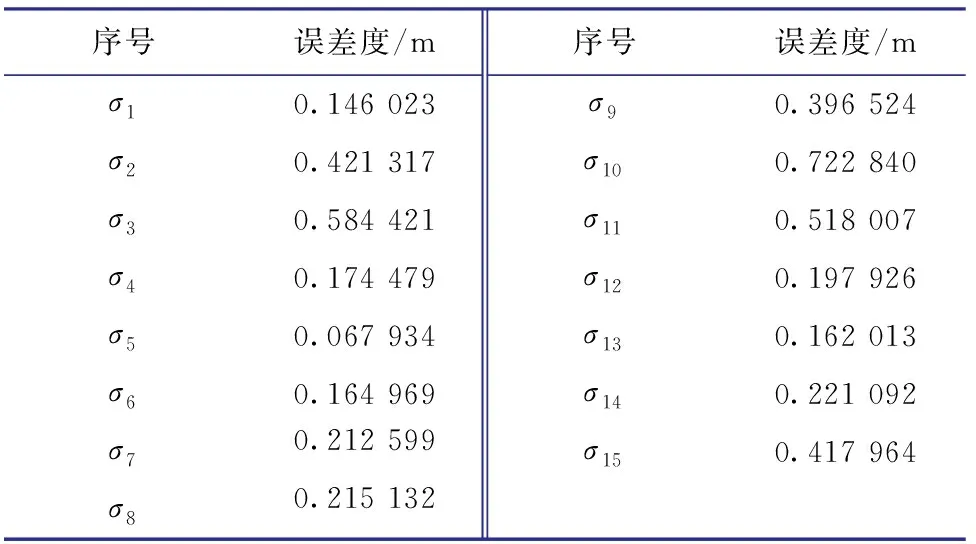
表4 电缆校验测井的误差度
有了误差度,根据式(9)计算得到各标准节箍深度的加权平均法最佳估计值(见表5),同时,为对比加权平均法和等精度平均法处理结果的差异,利用等精度平均法计算得到各标准节箍深度值(见表5)。
4 加权平均法处理结果可信度分析
为了验证利用加权平均法求取的标准节箍最佳深度估计值的准确性,利用计算数据(见表2)绘制了7个标准节箍深度测量值的概率密度曲线(见图1)[14],横坐标为标准节箍深度,纵坐标为对应深度值出现频率。
表5加权平均法和等精度平均法所求标准节箍深度值
Table5Standardcollardepthvaluescalculatedusingtheweightedaveragemethodandprecisionaveragemethod
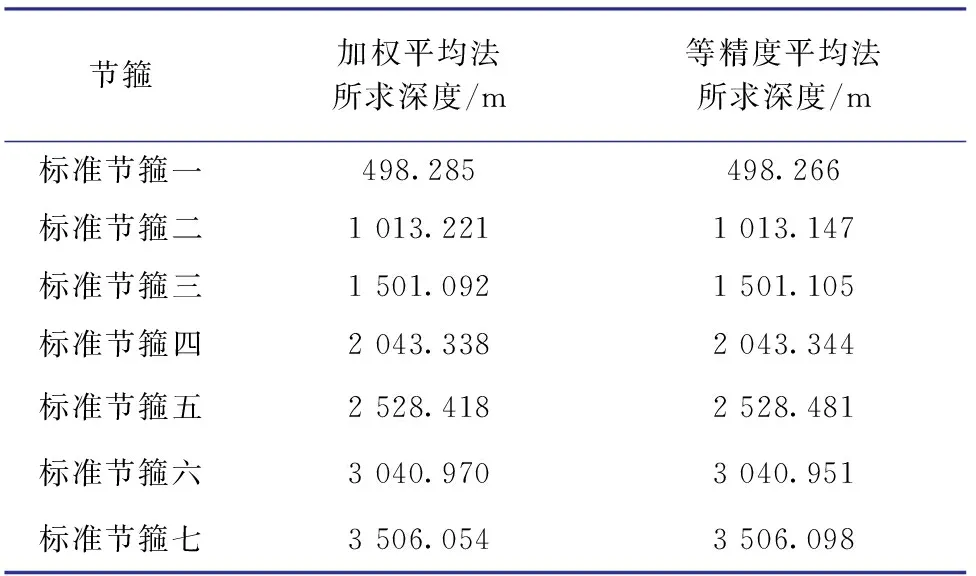
节箍加权平均法所求深度/m等精度平均法所求深度/m标准节箍一498.285498.266标准节箍二1 013.2211 013.147标准节箍三1 501.0921 501.105标准节箍四2 043.3382 043.344标准节箍五2 528.4182 528.481标准节箍六3 040.9703 040.951标准节箍七3 506.0543 506.098
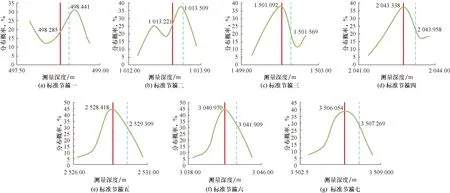
图1 标准节箍深度测量值概率密度曲线Fig.1 Probability density curve of standard collar depth
由图1可以看出,由于受测量数据次数有限的影响,概率密度曲线并不完全服从正态分布,以标准节箍一和节箍二最为突出,而其余节箍均服从类似正态分布。红色实线为利用加权平均法处理数据得到的标准节箍深度值,蓝色虚线为原始标准节箍深度值,利用加权平均法得到的标准节箍深度值的位置接近曲线的最高部位,而原始标准节箍深度值偏离较多,说明利用加权平均法得到的标准节箍深度值的可信度要高于原始标准节箍深度值。
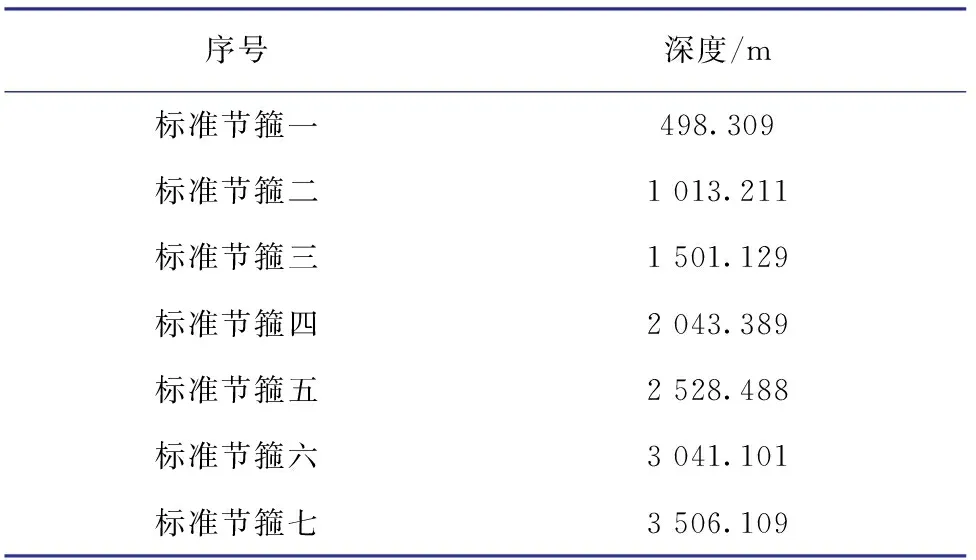
为对比加权平均法和等精度平均法2种处理结果的差异,利用等精度平均法计算出了各标准节箍深度的最佳估计值,并选择可靠性相对较高的辽河小数控测井设备所测结果(见表6)作为分析2种方法处理结果的参考值。
根据标准节箍相间距离,分别计算小数控所测量结果与加权平均法结果和等精度平均法结果的误差度[15],σ(加权平均)为0.001 440,σ(等精度平均)为0.004 801,σ(加权平均)小于σ(等精度平均)。
表6辽河小数控所测标准节箍深度
Table6StandardcollardepthvalueloggedbyLiaoheCNC
序号深度/m标准节箍一498.309标准节箍二1 013.211标准节箍三1 501.129标准节箍四2 043.389标准节箍五2 528.488标准节箍六3 041.101标准节箍七3 506.109
比较2种处理数据方法的处理结果,可以看出,利用加权平均法求取的最佳估计值比直接平均法求取的最佳估计值可信度更高,更加接近期望值。
5 结 论
1) 标准节箍深度测量值的概率密度曲线显示,利用多个深度标准井对新建标准井进行深度量值传递,避免了传递精度受制于单一深度标准井的节箍深度精度,深度值更接近概率密度曲线最高部位,其可信度和准确度远高于利用单井传递。
2) 利用加权平均法和直接平均法分别处理不等精度测量值求取最佳估计值的误差度表明,利用加权平均法求取的最佳估计值可信度更高。
3) 用于计算最佳估计值的测量次数越多,最佳估计值越接近期望值,所以随着柳X井测量数据的不断积累,应不断对标准节箍深度值进行校正,其可信度也将随测量次数的增多而不断提高。
参考文献
References
[1] 刘江伟,李建华,叶文军,等.测井电缆深度记号标定新方法实现的研究与应用[J].测井技术,2007,31(6):580-582.
Liu Jiangwei,Li Jianhua,Ye Wenjun,et al.A new method to calibrate magnetic depth mark of cable and its implementation[J].Well Logging Technology,2007,31(6):580-582.
[2] 吴凯华,张相山,王国龙,等,浅谈量值传递和量值溯源的实施[J].计量与测试技术,2013,40(1):52-53.
Wu Kaihua,Zhang Xiangshan,Wang Guolong,et al.Discussion implementation on the quantity value transfer and measurement traceability[J].Metrology & Measurement Technique,2013,40(1):52-53.
[3] Q/SY 1557-2012 测井电缆深度标准井技术规范[S].
Q/SY 1557-2012 Technical specification for well logging calbe depth standard well[S].
[4] 林浩,王铁刚,邓基华.井眼深度测量及校正[J].石油仪器,2005,19(1):77-78.
Lin Hao,Wang Tiegang,Deng Jihua.Borehole depth measurement and correction[J].Potroleum Instruments,2005,19(1):77-78.
[5] 王辉,吕海霞,潘俊辉,等.基于相对幅值法的接箍深度识别方法[J].哈尔滨商业大学学报:自然科学版,2012,28(4):435-438.
Wang Hui,lv Haixia,Pan Junhui,et al.Study on collar depth identification based on relative amplitude method[J].Journal of Harbin University of Commerce:Natural Sciences Edition,2012,28(4): 435-438.
[6] 罗厚义,汤达祯.中东某油田测井深度系统的误差分析及解决案例[J].西部探矿工程,2013,25(4):43-45.
Luo Houyi,Tang Dazhen.Case of well logging depth system error analysis and its solution in an oil field of Middle East[J].West-China Exploration Engineering,2013,25(4):43-45.
[7] 罗荣,黄国光.超深井测井深度质量控制方法探讨[J].石油工业技术监督,2012,30(4):21-24.
Luo Rong,Huang Guoguang.Discussions on the quality control method for the logging depth of ultradeep wells[J].Technology Supervision in Petroleum Industry,2012,30(4):21-24.
[8] 芦立娟,鲁晓东,竺江峰.“加权平均”法在不等精度测量中的运用[J].大学物理实验,2003,16(4):53-54.
Lu Lijuan,Lu Xiaodong,Zhu Jiangfeng.Application of weighted average method to non-precise measurement[J].Physical Experiment of College,2003,16(4):53-54.
[9] 廖东良,肖立志,张元春.基于矿物组分与断裂韧度的页岩地层脆性指数评价模型[J].石油钻探技术,2014,42(4):37-41.
Liao Dongliang,Xiao Lizhi,Zhang Yuanchun.Evaluation model for shale brittleness index based on mineral content and fracture toughness[J].Petroleum Drilling Techniques,2014,42(4):37-41.
[10] 陶靖轩,顾龙芳,宋明顺,等.不等精度测量结果标准差的估计[J].计量学报,2012,33(1):94-96.
Tao Jianxuan,Gu Longfang,Song Mingshun,et al.Estimation of standard deviation in unequal precision measurement[J].Acta Metrologica Sinica,2012,33(1):94-96.
[11] 周拥军,邓才华.加权和不加权TLS方法及其在不等精度坐标变换中的应用[J].武汉大学学报:信息科学版,2012,37(8):976-979.
Zhou Yongjun,Deng Caihua.Weighted and unweighted total least square methods and applications to heteroscedastic 3D coordinate transformation[J].Geomatics and Information Science of Wuhan University,2012,37(8):976-979.
[12] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2010:14-15.
Fei Yetai.Error theory and data processing[M].Beijing:China Machine Press,2010:14-15.
[13] 张德根.单摆实验中不等精度测量的不确定度分析[J].大学物理实验,2013,26(6):92-94.
Zhang Degen.Uncertainty analysis of unequally accurate measurement in the single pendulum experiment[J].Physical Experiment of College,2013,26(6):92-94.
[14] 陶靖轩,王敏华,刘春雨.应用统计学[M].北京:中国计量出版社,2003:125-130.
Tao Jingxuan,Wang Minghua,Liu Chunyu.The application of statistics[M].Beijing: China Metrology Publishing House,2003:125-130.
[15] 倪燕茹.基于测量不确定度评定的数据处理方法[J].大学物理实验,2012,25(1):68-70.
Ni Yanru.The method of data processing based on uncertainty in measurement[J].Physical Experiment of College,2012,25(1):68-70.
