储/隔层岩石及层间界面性质对压裂缝高的影响
2014-09-06邓金根蔚宝华陈建国
李 扬, 邓金根, 蔚宝华, 刘 伟, 陈建国
(油气资源与探测国家重点实验室(中国石油大学(北京)),北京 102249)
水力压裂在非常规油气资源开发中具有重要作用,但该技术的成功率并不高,其中一个重要原因是最大施工压力预测不准确,缺少对隔层中压裂缝高的有效控制方法。国内外许多学者就地层弹性模量、地应力、断裂韧性以及界面性质等因素对压裂缝高的影响进行了研究:Liu He等人[1]研究了孔隙度和泥质含量对水力压裂缝高的影响;Gu Hongren等人[2]通过三维模拟试验得出,除地应力之外,弹性模量对压裂缝高的影响也较为明显,当裂缝未进入隔层时,弹性模量大的隔层对缝高扩展起阻碍作用,当裂缝已扩展进入隔层时,弹性模量小的隔层对缝高限制效果较好;M.B.Smith等人[3]认为仅凭储/隔层弹性模量之间的差异不足以影响裂缝缝高的扩展;A.A.Daneshy和R.D.Barree等人[4-7]认为储/隔层界面之间的剪切滑移是影响缝高的重要因素之一;G.Anderson[8]通过试验证实了界面之间存在剪切滑移的可能;黄荣樽[9]指出界面抗剪强度一方面可能源于层间胶结物的粘合力,另一方面可能来源于抵抗变形的摩擦力产生的机械联结力;周文高等人[10]研究了岩石物质特性、施工参数、地应力差和裂缝上下端阻抗对缝高的影响;M.K.Fisher等人[11]根据实际压裂作业的微地震数据,从地应力、岩性、弱面、断层、压裂液梯度和岩石渗透性等方面讨论了压裂缝缝长和缝高的扩展;陈治喜等人[12]认为在一定的地应力条件下,裂缝能否向隔层扩展以及扩展范围的大小取决于作业压力的大小;王瀚等人[13]利用二维平面应变非线性流固耦合水力压裂模型对裂缝高度的扩展进行了模拟,极大地减小了计算量。总体而言,现有研究成果主要从岩石力学特性和地应力差两方面来评价隔层控制缝高的能力,但是就部分岩石力学性质对缝高的影响而言还存在争议,而且影响裂缝缝高的因素特别多,各参数的影响程度并不明确,储/隔层界面性质对裂缝缝高的影响缺乏有效的评价方法。鉴于此,笔者基于有限元软件ABAQUS研究了储/隔层岩石弹性模量、地应力和抗拉强度等因素对水力裂缝缝高扩展的影响,并着重分析了储/隔层界面性质的影响。
1 Cohesive单元损伤模型
有限元计算平台ABAQUS中的Cohesive单元基于损伤力学原理、采用刚度衰减的方法模拟介质中裂缝的起裂与扩展,并且可以模拟裂缝扩展过程中压裂液的流动与滤失,比较适合用来模拟水力压裂裂缝的扩展。
1.1 Cohesive单元损伤模式
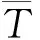
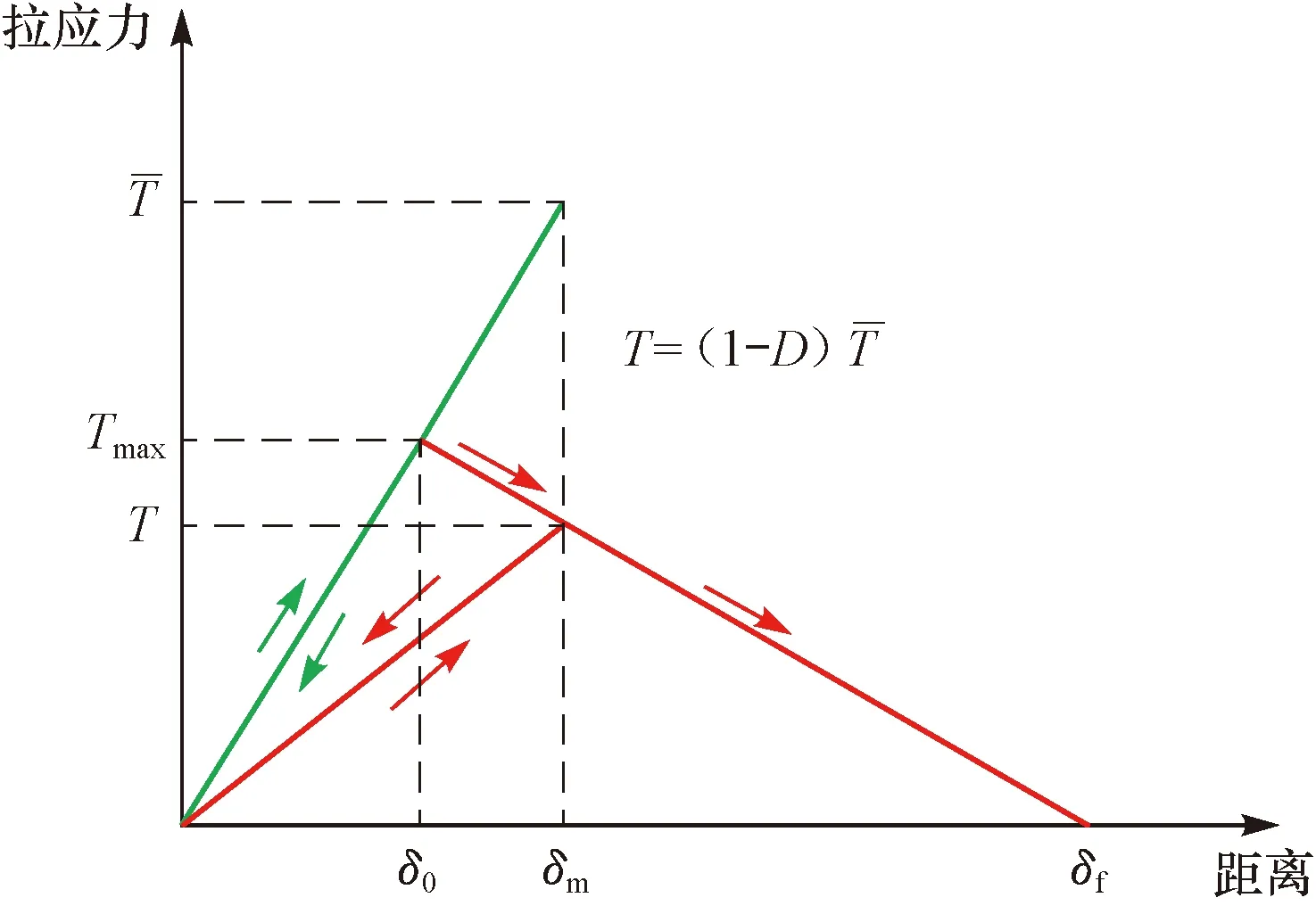
图1 Cohesive单元损伤T-S准则Fig.1 The traction-separation law of Cohesive element damage
该T-S准则是以Cohesive单元承受的拉应力为损伤判据,单元在损伤之前其刚度非常大,所受应力与位移成正比,卸载后可以恢复,但当拉应力超过材料抗拉强度之后,其能承受的应力随着位移的增加呈线性衰减,并且不可恢复。该准则常用来模拟岩石、混凝土等材料中裂缝的扩展,比较适合于模拟水力压裂中裂缝的扩展过程。
1.2 Cohesive单元的起裂与扩展准则
笔者所采用的Cohesive单元的起裂准则为二次应力准则,其表达式为[15]:
(1)
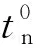
Cohesive单元采用刚度退化来描述单元的损伤演化过程,其表达式为:
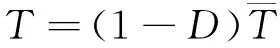
(2)
损伤因子的计算公式为[16]:
(3)
1.3 Cohesive单元损坏区的流体流动
Cohesive单元损坏区的流体流动分为沿Cohesive单元的切向流动和垂直于Cohesive单元上下表面的法向滤失,如图2所示。
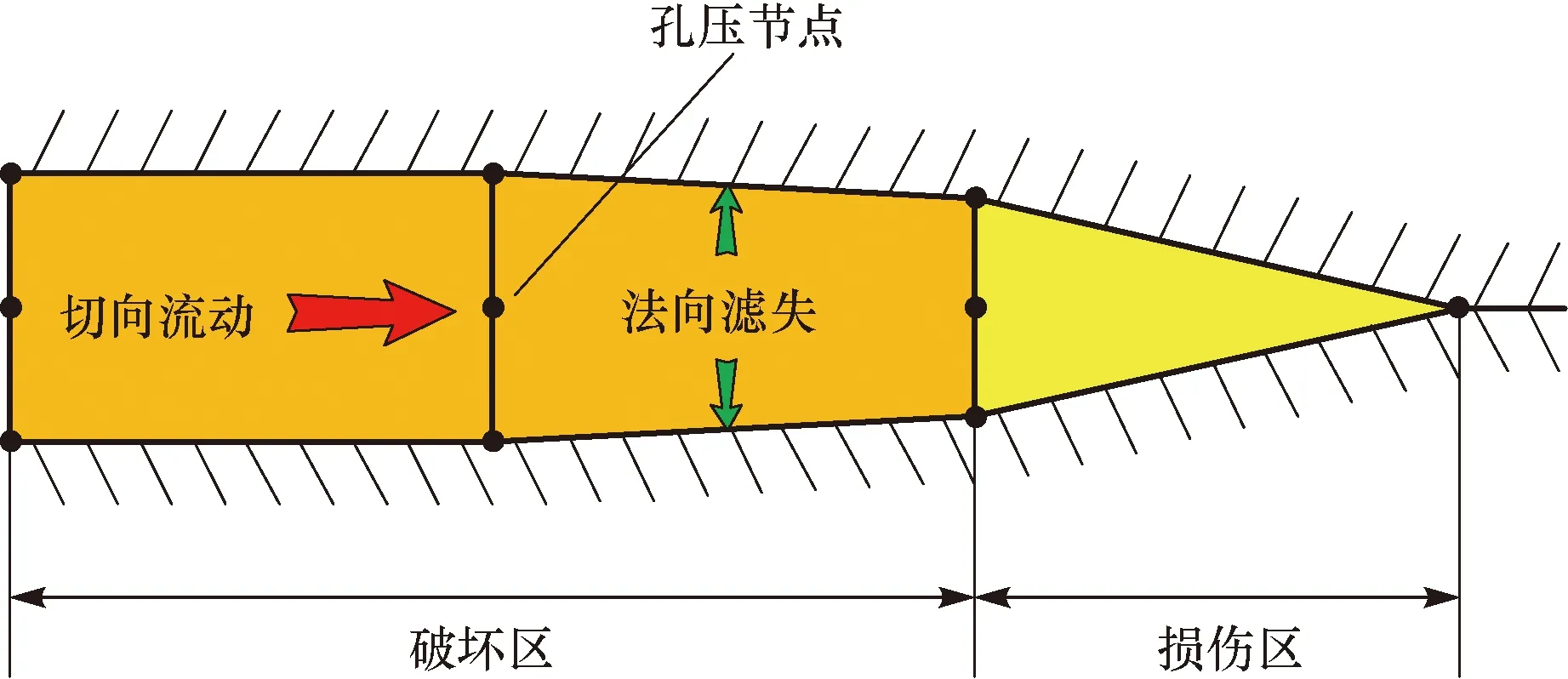
图2 Cohesive单元损坏区流体流动示意Fig.2 The fluid flow schematic within a damaged Cohesive zone
假设Cohesive单元内部流体为不可压缩的牛顿流体,其切向流动的计算式为[17]:
(4)
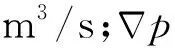
Cohesive单元上下表面法向方向的滤失可描述为[18]:
(5)
式中:pt,pb分别为裂缝上下表面处的孔隙压力,Pa;pf为裂缝内的流体压力,Pa;ct,cb分别为上下表面的滤失系数,m3/(Pa·s);qt,qb分别为上下表面的法向体积流量,m3/s。
Cohesive单元的流体质量守恒方程为[19]:
(6)
式中:Q(t)为压裂流体注入速度,m3/s。
2 计算模型及结果分析
为了研究各因素对缝高的影响,根据界面的胶结程度分了2种情况:一种界面胶结完好,界面不产生滑移;另一种界面胶结不完全,储/隔层之间可能会产生滑移。假定井为垂直井,地层为水平层状均质地层,建立了如图3所示的计算模型。该模型中,竖直方向设置Cohesive单元模拟水力裂缝的垂向扩展,水平方向设置Cohesive单元层间界面性质,水平Cohesive单元可以模拟界面的拉伸破坏和剪切破坏。
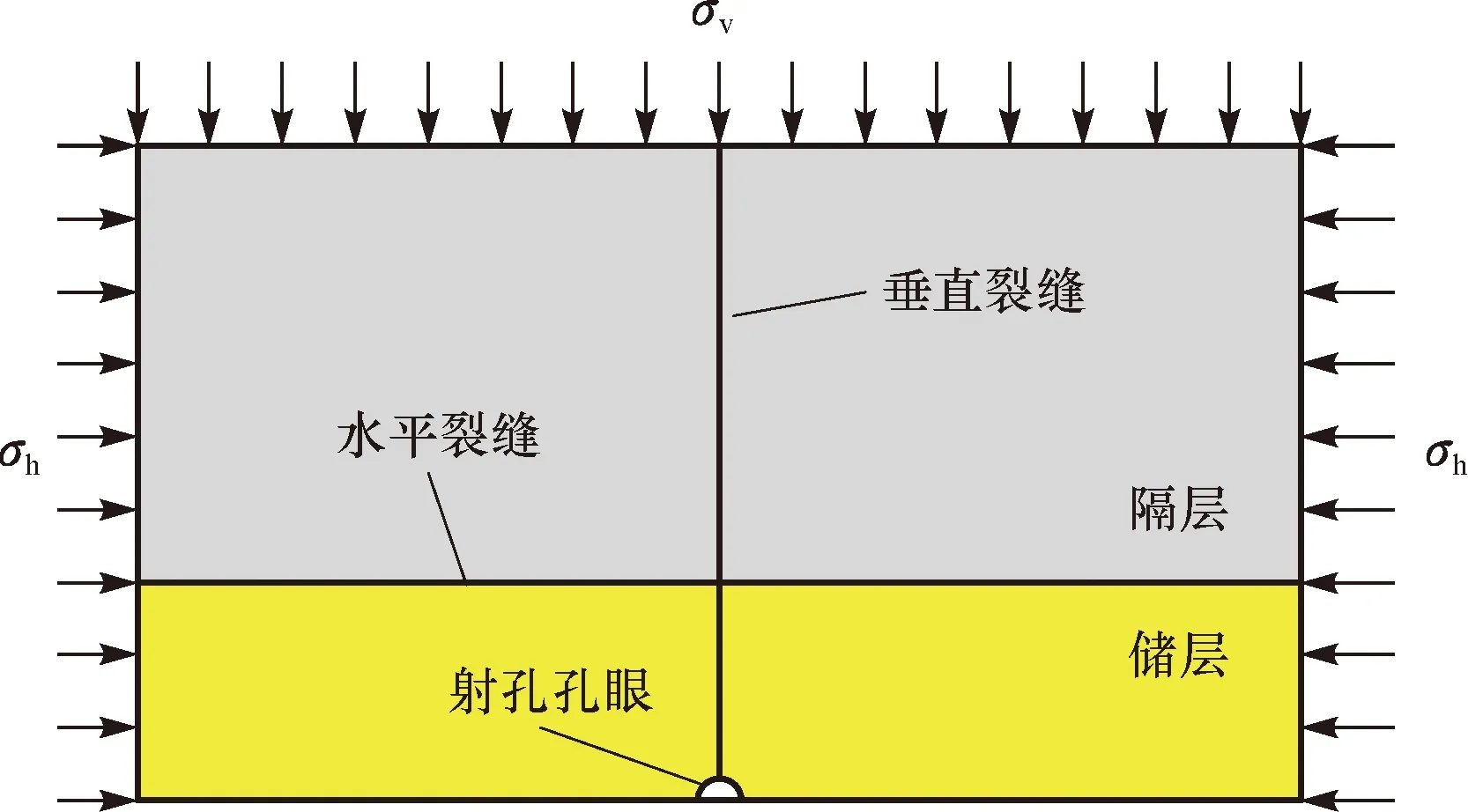
图3 计算模型示意Fig.3 Sketch of computational model
2.1 界面胶结完好条件下的情况
假定产层与隔层之间胶结完好,界面不会产生滑移,讨论隔层和储层的弹性模量、地应力以及抗拉强度等参数对缝高的影响(计算模型见图3)。模型储层厚度5 m,隔层厚度30 m,宽度50 m。左右两侧分层施加非均匀最小水平主应力,上边界施加上覆岩层压力,下边界设置为关于y轴的对称边界条件,左右和上边界保持恒定的孔隙压力(34 MPa),初始孔隙压力为34 MPa,初始孔隙度为0.15。由于模型为平面应变,因此模型中的泵注排量根据现场排量2~3 m3/min进行相应的折减,设置为0.012 m3/min,持续600 s,压裂液的黏度为100 mPa·s,其他的主要计算参数初始值见表1和表2。
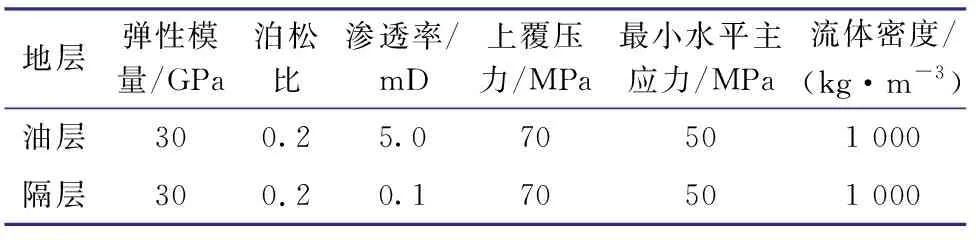
表1 地层岩石力学参数Table 1 The rock mechanics parameters of the stratum

表2 Cohesive单元材料参数Table 2 The material parameters of Cohesive elements
2.1.1 弹性模量对压裂缝高的影响
储层岩石的弹性模量取30 GPa,隔层的弹性模量分别取20、30、40和50 GPa,其他材料参数值见表1和表2,研究隔层岩石弹性模量对裂缝缝高的影响,结果如图4所示。从图4可以看出,隔层弹性模量越大,裂缝在隔层扩展的高度越大。分析认为,这是因为弹性模量大会使裂缝的宽度变窄,在注入流体体积和滤失量一定的情况下,裂缝高度就会相应增大。同时,岩石的弹性模量越大,越容易在裂缝尖端形成高应力,在同样的抗拉强度条件下岩石更容易向前扩展。因此,弹性模量小的隔层对控制压裂缝高有利。
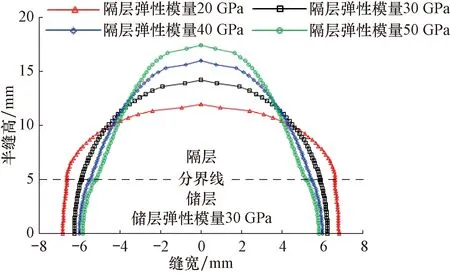
图4 不同隔层弹性模量下的裂缝形态Fig.4 Fracture shapes with different elastic modulus of insulating layers
图5为压裂过程中井底压力随时间的变化曲线,并标出了裂缝扩展穿过储/隔层界面时的井底压力。
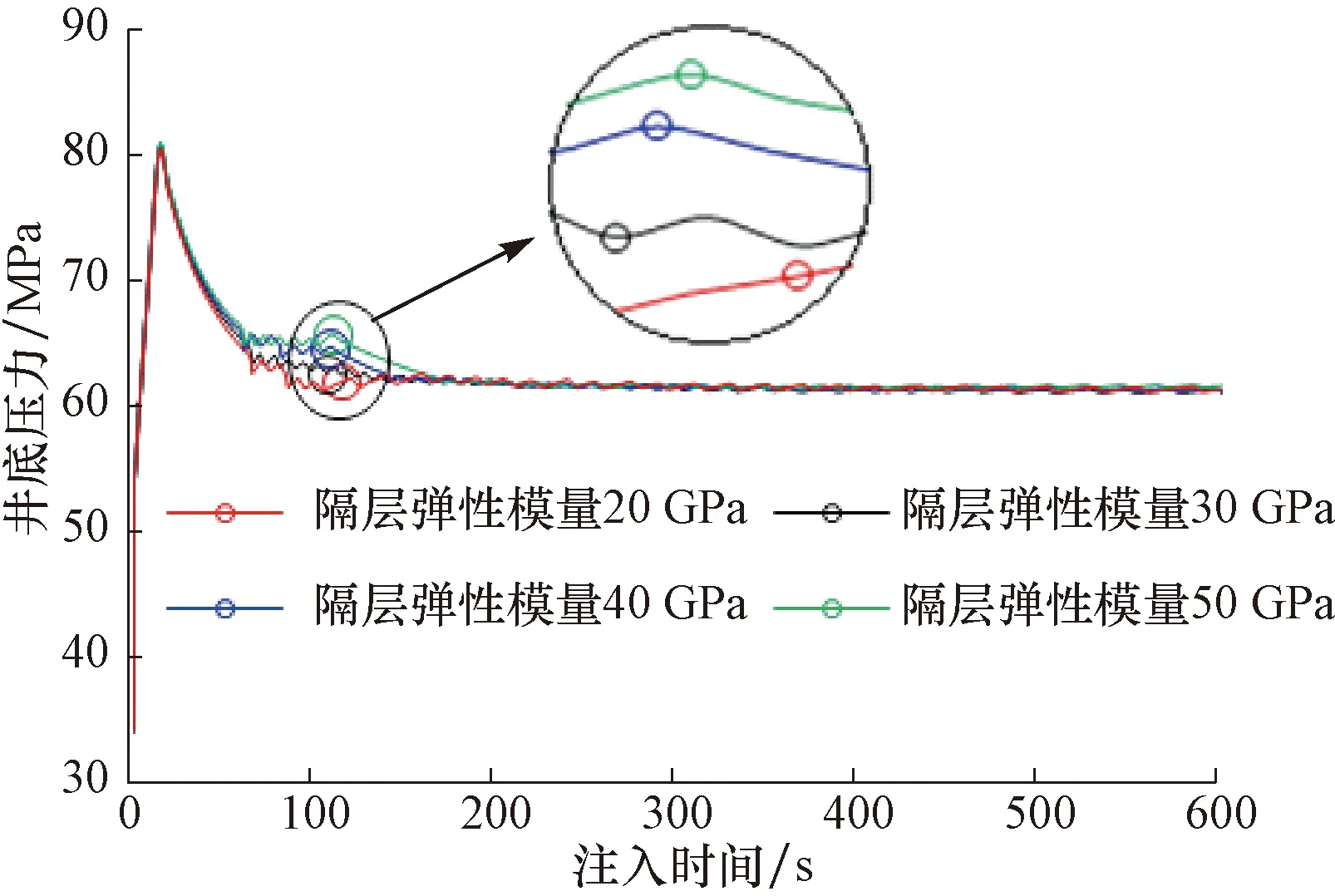
图5 不同隔层弹性模量下的井底压力Fig.5 Bottom hole pressure with different elastic modulus of insulating layers
从图5可以看出,随隔层弹性模量增大,裂缝从储层进入隔层时刻的井底压力会略微增大,说明隔层弹性模量大对裂缝扩展进入隔层确实有阻碍作用,但是阻碍效果不明显,和现场施工过程中的压力波动相比几乎可以忽略。
综合分析图4、图5可知,当泵入排量不足以使裂缝扩展至分界面时,隔层弹性模量大对缝高延伸起限制作用;而一旦裂缝已经进入隔层,弹性模量大的隔层其缝宽相对较小,由压裂液体积守恒可知,缝高会急剧增大,压穿隔层进入水层的风险增大。
2.1.2 地应力对压裂缝高的影响
计算参数值取自表1和表2,逐渐改变隔层岩石的最小水平主应力(分别为50、52、54、56和58 MPa),研究隔层最小水平主应力对裂缝缝高的影响,结果如图6所示。从图6可以看出,隔层的最小水平主应力越大,隔层中裂缝的宽度和高度越小,储层中裂缝的宽度越大。分析认为,这是因为裂缝宽度与净压力相关,隔层的最小水平主应力越大,那么储层中的净压力就相对越大,压裂液就能更多地停留在储层中。
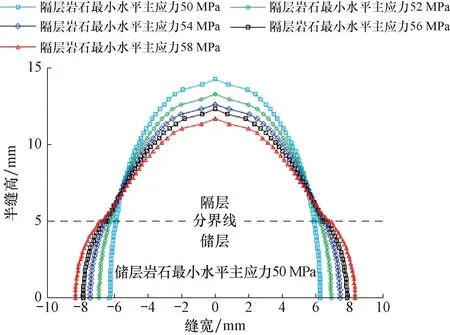
图6 不同隔层地应力下的裂缝形态Fig.6 Fracture shapes with different in-situ stress of insulating layers
2.1.3 抗拉强度差对压裂缝高的影响
计算参数值取自表1和表2,逐渐改变隔层岩石的抗拉强度(分别为4、7、10、13和16 MPa),研究隔层抗拉强度对裂缝缝高的影响,结果如图7所示。
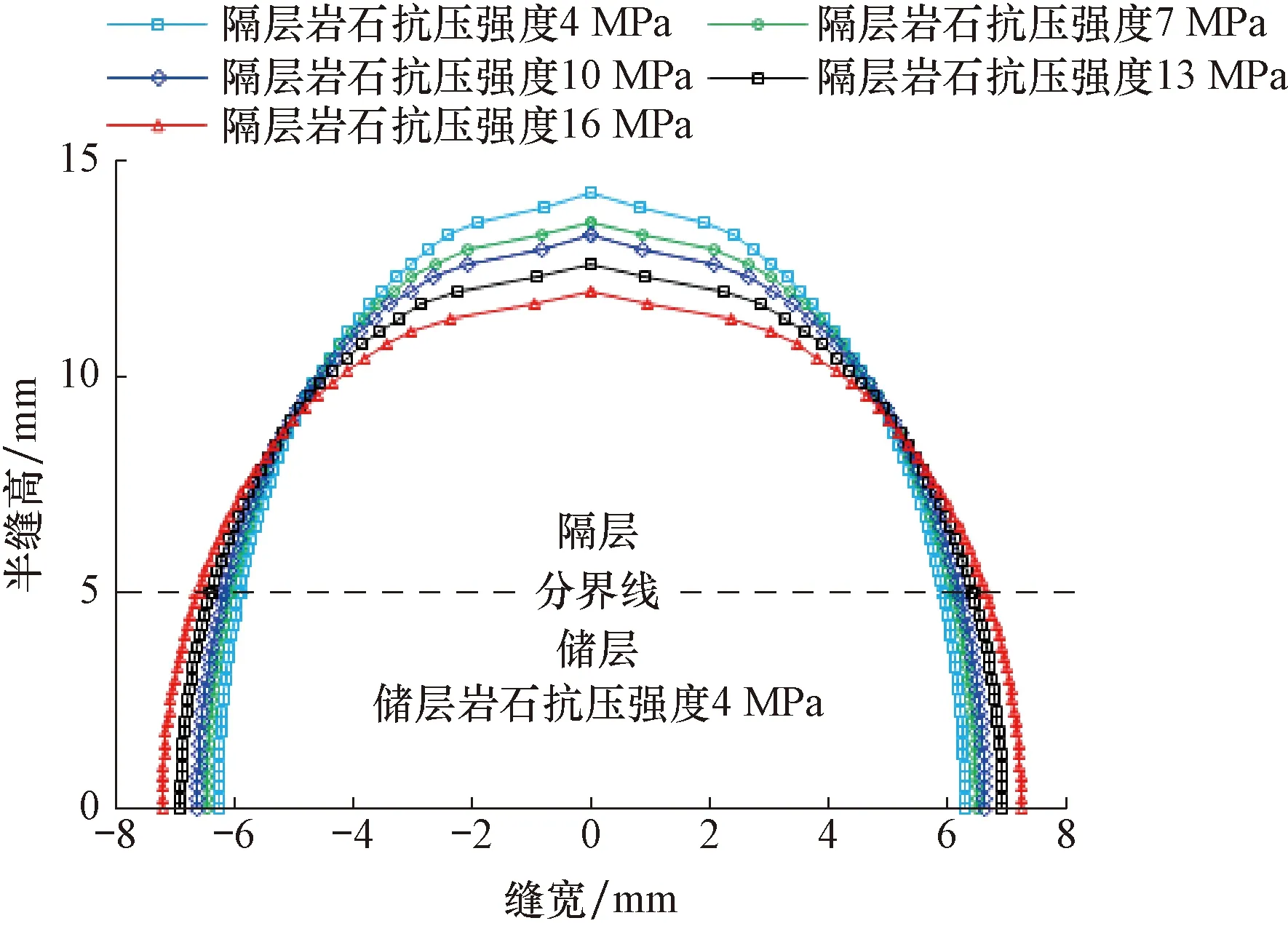
图7 不同隔层抗拉强度下的裂缝形态Fig.7 Fracture shapes with different tensile strength of insulating layers
从图7可以看出,隔层的抗拉强度越大,裂缝的高度就越小。分析认为,这是因为裂缝必须克服岩石的抗拉强度才能继续向前扩展。因此,高抗拉强度的隔层也会限制裂缝缝高的扩展。
通过分析界面完全胶结时储/隔层弹性模量、地应力和抗拉强度可知,弹性模量对水力裂缝的起裂影响较小,但是对裂缝扩展的影响较大,地应力和抗拉强度对裂缝起裂与扩展的影响均较大。总体来说,地应力大、抗拉强度高和弹性模量小的隔层有利于控制缝高。
2.2 界面不完全胶结条件下的情况
假设储层和隔层界面不完全胶结,分层界面之间存在着一定量的胶结物,并且在上覆岩层压力作用下有一定程度的压实,能够承受一定的拉应力和剪应力。在该情况下裂缝能否穿过界面进入隔层受到多种因素的影响,其中包括层间地应力、力学参数以及界面自身的性质。关于层间地应力和力学参数对裂缝缝高的影响,已经在前文讨论,以下主要讨论层间界面性质对压裂缝高的影响。
2.2.1 界面抗剪强度对裂缝高度的影响
储层和隔层界面抗剪强度应广义地理解为2部分:一是界面胶结物本身的抗剪强度,二是在上覆岩层压力作用下由于接触界面比较粗糙引起的摩擦强度。对于储/隔层界面的广义抗剪强度,可以依据弱面理论表示为[20]:
τ=Cw+σtanφw
(7)
式中:τ为结构面的抗剪强度,Pa;Cw为结构面内聚力,Pa;σ为结构面上的法向应力,Pa;φw为结构面有效摩擦角,(°)。
文献[21]给出了各类软弱结构面的抗剪强度,根据测井解释的岩层性质可以查出对应结构面的内聚力和有效摩擦角,从而能确定界面抗剪强度。
水力压裂过程中通常有以下2种情况:一是层间界面抗剪强度小于隔层抗拉强度与最小水平主应力之和,此时水力裂缝将会完全被限制在产层里面,界面处产生滑移;二是当层间界面抗剪强度足够大,界面处会发生部分滑移,但还是会扩展进入隔层。
计算模型见图3,计算参数见表3。

表3 地层岩石力学参数Table 3 The rock mechanics parameters of the stratum
分别研究了界面抗剪强度为50、58和66 MPa时不同注入时间下裂缝的形态演化情况,并以裂纹中心为(0,0)点,绘制了裂缝缝高的几何形态,见图8—11。
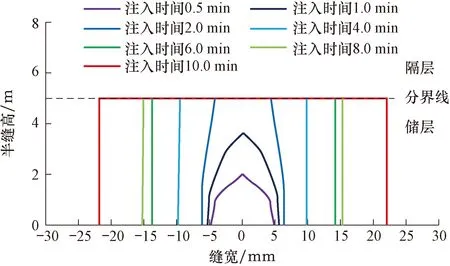
图8 界面抗剪强度为50 MPa时不同注入时间下裂缝形态的演化Fig.8 Evolution of fracture shapes with 50 MPa of interface shear strength at different injection times
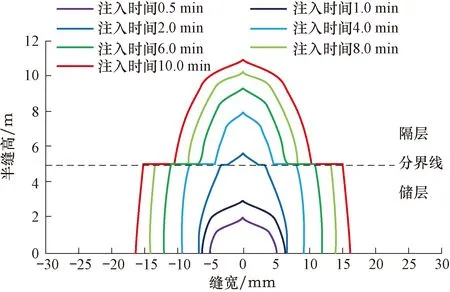
图9 界面抗剪强度为58 MPa时不同注入时间下裂缝形态的演化Fig.9 Evolution of fracture shapes with 58 MPa of interface shear strength at different injection times
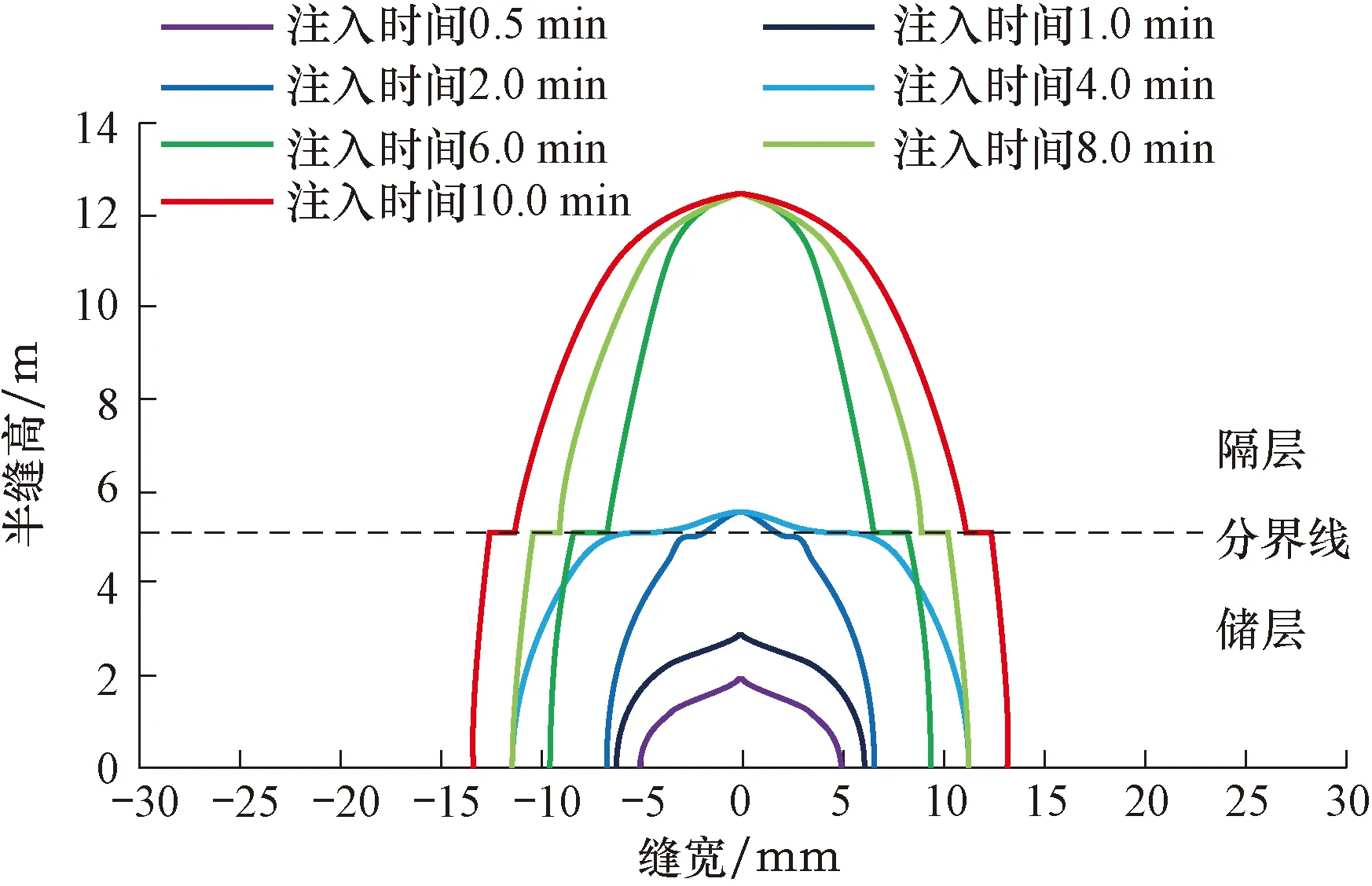
图10 界面抗剪强度为66 MPa时不同注入时间下裂缝形态的演化Fig.10 Evolution of fracture shapes with 66 MPa of interface shear strength at different injection times
从图8可以看出,当层间界面抗剪强度为50 MPa时,产层在层间界面处完全滑移,隔层不会起裂。从图9可以看出,当层间界面抗剪强度为58 MPa时,大于隔层最小水平主应力与抗拉强度之和,产层在层间界面处部分产生滑移,同时裂缝也扩展至隔层。
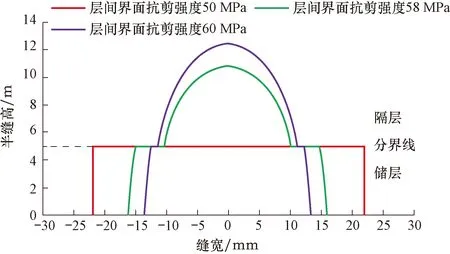
图11 不同界面抗剪强度下的裂缝形态Fig.11 Fracture shapes with different interface shear strength
从图10可以看出,当层间界面抗剪强度为66 MPa时,产层在层间界面处产生部分滑移,裂缝也扩展至隔层。比较注入时间为4和6 min时的裂缝形态可以看出,当裂缝进入隔层之后,储层的裂缝宽度会有一个减小的过程,这是因为裂缝扩展进入高应力的隔层后,储层内压裂液压力会有一个释放的过程。
从图11可以看出,层间界面抗剪强度越大,水力裂缝进入隔层的可能性越大,层间滑移越小,同时裂缝上窜的高度越大。
水力裂缝扩展至储/隔层交界面后,通常情况下只有当界面抗剪强度大于隔层最小水平主应力与隔层抗拉强度之和这一临界值时,裂缝才会扩展至隔层,但是水力裂缝的缝长方向通常延伸得较远,难免有某些地方的隔层本身存在天然微裂隙,此时若有压裂液渗入其中,即使界面的抗剪强度很低,水力裂缝也有可能扩展进入隔层。
2.2.2 界面上覆岩层压力对裂缝高度的影响
当上覆岩层压力远大于最大和最小水平主应力时,难以形成水平裂缝或T形裂缝。但对于逆断层发育和浅层等构造运动相对强烈的地区,上覆岩层压力小于或相近于水平地应力,则非常容易形成水平裂缝。因此,对于深部地层,可能存在层间水平地应力相差较大的情况,比如上覆岩层压力在储层是最大主应力,但是在隔层可能是中间主应力。这种情况下,当层间界面胶结强度较低时,裂缝容易在界面处转向,沿着界面扩展,形成T形裂缝,限制裂缝高度扩展。可以用如下关系式来判定能否形成此类T形裂缝:
σhb+Stb>σv+St>σhp+Stp
(8)
式中:σhb为隔层最小水平主应力,MPa;Stb为隔层抗拉强度,MPa;σhp为储层最小水平主应力,MPa;Stp为储层抗拉强度,MPa;σv为界面处的上覆岩层压力,MPa;St为界面抗拉强度,MPa。
当σv+St<σhp+Stp时,会直接在储层产生水平裂缝;当σv+St>σhb+Stb时,裂缝会直接穿透界面进入隔层或者在储/隔层界面产生滑移;当σhb+Stb>σv+St>σhp+Stp时,在储层形成垂直裂缝,并沿层间界面转向形成水平裂缝。
为验证此准则的正确性,利用图3所示模型进行了2组数值模拟试验,计算参数值见表4,其他参数值与表3相同。

表4 数值试验参数Table 4 The parameters of numerical experiments
数值试验1和2分别满足关系式(9)和(10):
σv+St=58>σhb+Stb=57.8
(9)
σv+St=57<σhb+Stb=57.8
(10)
对上述2种情况分别进行数值计算,结果如图12和图13所示。

图12 数值模拟试验1结果Fig.12 The result of the numerical experiment 1

图13 数值模拟试验2结果Fig.13 The result of the numerical experiment 2
由图12和图13可知,当地层条件满足式(8)时,水力裂缝扩展至储/隔层界面后会发生转向形成T形缝。
3 结 论
1) 弹性模量小、地应力大和抗拉强度高的隔层对缝高能够起到一定的限制作用,其中地应力差的限制作用最为明显。在裂缝进入隔层之前,弹性模量大的隔层可以对裂缝进入隔层起到一定的阻碍作用,但裂缝进入隔层后弹性模量小的隔层对缝高有较好的限制作用。弹性模量对裂缝的起裂影响较小,仅凭储/隔层之间弹性模量的差异难以将裂缝完全限制在储层内。
2) 除弹性模量、地应力外,储/隔层界面滑移也是影响压裂缝高的主要因素之一,当界面抗剪强度低于某一临界值时,裂缝尖端可能在界面处产生滑移,使裂缝上端变钝,能有效限制裂缝沿垂向扩展。界面的抗剪强度是水力压裂作业裂缝能否进入隔层的重要判断指标之一,其中储/隔层界面的抗剪强度可以用弱面准则来估算。
3) 上覆岩层压力对裂缝的形态也存在一定的影响,在特定上覆岩层压力等地层条件下可能产生T形缝。给出了在逆断层控制区域产生T形缝的判断准则,并用数值模拟试验对其进行了验证。
参考文献
References
[1] Liu He,Wang Han,Wu Heng’an,et al.Effect of reservoir porosity and clay content on hydraulic fracture height containment[R].IPTC 16415,2013.
[2] Gu Hongren,Siebrits E.Effect of formation modulus contrast on hydraulic fracture height containment[R].SPE 103822,2006.
[3] Smith M B,Bale A B,Britt L K,et al.Layered modulus effects on fracture propagation,proppant placement,and fracture modeling[R].SPE 71654,2001.
[4] Daneshy A A.Factors controlling the vertical growth of hydraulic fractures[R].SPE 118789,2009.
[5] Daneshy A A.Hydraulic fracture propagation in layered formations[J].SPE Journal,1978,18(1):33-41.
[6] Daneshy A A.Hydraulic fracture propagation in the presence of planes of weakness[R].SPE 4852,1974.
[7] Barree R D,Winterfeld P H.Effects of shear planes and interfacial slippage on fracture growth and treating pressures[R].SPE 48926,1998.
[8] Anderson G.Effects of friction on hydraulic fracture growth near unbonded interfaces in rocks[J].SPE Journal,1981,21(1):21-29.
[9] 黄荣樽.水力压裂裂缝的起裂和扩展[J].石油勘探与开发,1981,8(5):62-74.
Huang Rongzun.The initiation and propagation of hydraulic fracture[J].Petroleum Exploration and Development,1981,8
(5):62-74.
[10] 周文高,胡永全,赵金洲,等.控制压裂缝高技术研究及影响因素分析[J].断块油气田,2006,13(4):70-72.
Zhou Wengao,Hu Yongquan,Zhao Jinzhou,et al.Research on fracture height containment technology and analysis of influence factors[J].Fault-Block Oil & Gas Field,2006,13(4):70-72.
[11] Fisher M K,Warpinski N R.Hydraulic-fracture-height growth:real data[J].SPE Production & Operations,2012,27(1):8-19.
[12] 陈治喜,陈勉,黄荣樽,等.层状介质中水力裂缝的垂向扩展[J].石油大学学报:自然科学版,1997,21(4):23-26,32.
Chen Zhixi,Chen Mian,Huang Rongzun,et al.Vertical growth of hydraulic fracture in layered formations[J].Journal of the University of Petroleum,China:Edition of Natural Science,1997,21(4):23-26,32.
[13] 王瀚,刘合,张劲,等.水力裂缝的缝高控制参数影响数值模拟研究[J].中国科学技术大学学报,2011,41(9):820-825.
Wang Han,Liu He,Zhang Jin,et al.Numerical simulation of hydraulic fracture height control with different parameters[J].Journal of University of Science and Technology of China,2011,41(9):820-825.
[14] Tomar V,Zhai Jun,Zhou Min.Bounds for element size in a variable stiffness cohesive finite element model[J].International Journal for Numerical Methods in Engineering,2004,61(11):1894-1920.
[15] Camanho P P,Dávila C G.Mixed-mode decohesion finite elements for the simulation of delamination in composite materials[R].NASA/TM-2002-211737,2002.
[16] Turon A,Camanho P P,Costa J,et al.A damage model for the simulation of delamination in advanced composites under variable-mode loading[J].Mechanics of Materials,2006,38(11):1072-1089.
[17] Economides M J,Nolte K G,Ahmed U.Reservoir stimulation[M].Chichester:Wiley,2000:5.15-5.16.
[18] Hagoort J,Weatherill B,Settari A.Modeling the propagation of waterflood-induced hydraulic fractures[J].SPE Journal,1980,20(4):293-303.
[19] Peirce A,Detournay E.An implicit level set method for modeling hydraulically driven fractures[J].Computer Methods in Applied Mechanics and Engineering,2008,197(33-40):2858-2885.
[20] Fjar E,Holt R M,Raaen A M,et al.Petroleum related rock mechanics[M].2nd ed.Amsterdam:Elsevier,2008:60-64.
[21] 贾喜荣.岩石力学与岩层控制[M].徐州:中国矿业大学出版社,2010:111-114.
Jia Xirong.Rock mechanics and strata control[M].Xuzhou:China University of Mining and Technology Press,2010:111-114.
