考虑非达西效应的致密气藏裂缝参数优化设计
2014-09-06孙元伟程远方张矿生王怀栋
孙元伟, 程远方, 张矿生, 常 鑫, 王怀栋
(1.中国石油大学(华东)石油工程学院,山东青岛 266580;2.中国石油长庆油田分公司油气工艺研究院,陕西西安 718500)
致密气藏一般渗透率较低,需要进行压裂施工[1-3],因此,致密气藏压裂优化设计显得格外重要,且压裂后压裂液破胶以及裂缝内气体的非达西流动对裂缝渗透率有很大影响[4-7],需要加以考虑。压裂优化设计一般是借助裂缝模拟、气藏模拟及经济评价,以经济最优化、压裂后产量相对最大化或压裂后面积波及系数最大化等为目标函数,或采用多目标函数进行优化设计[8-10],但是这些设计方法都难以保证压裂效果的长效性。致密气藏压裂裂缝一般设计为长而导流能力低的支撑裂缝,但是低导流能力的长缝,在地下条件下,导流能力衰减快,很容易造成裂缝失效。因此,需要同时优化裂缝的长度和导流能力,使致密气藏采气指数最大化成为关键问题。R.Oligeny等人[11]提出了支撑剂指数的概念,使同时优化裂缝长度和裂缝导流能力成为可能。因此,笔者在支撑剂指数概念的基础上,考虑非达西流动对致密气藏裂缝有效渗透率的影响,建立无因次采气指数、支撑剂指数和无因次裂缝有效导流能力的关系函数,通过迭代法求得最优裂缝参数。
1 支撑剂指数
1.1 支撑剂指数的概念
R.Oligeny等人定义支撑剂指数的概念为[11]:
(1)
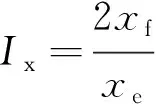
(2)
(3)
式中:Np为支撑剂指数;Kf为裂缝渗透率,mD;K为基质渗透率,mD;Vp为支撑剂体积,m3;Vres为气藏体积,m3;Ix为穿透比;xf为裂缝单翼缝长,m;xe为气藏边长,m;CfD为无因次裂缝导流能力;wp为裂缝平均宽度,m。
支撑剂指数有两方面的意义:一是表示裂缝和气藏规模以及渗透率的比值,特别是对于已知气藏,反映了压裂施工规模和气藏规模的关系;二是反映了裂缝空间资源的分配问题,在裂缝体积一定时,反映了裂缝长度和裂缝导流能力的配置问题[11-12]。
1.2 考虑裂缝有效渗透率的支撑剂指数
致密气藏中气体在裂缝内的非达西流动会对裂缝的有效渗透率产生很大影响[7,13-16],为使优化设计结果更加准确,要对式(1)中的裂缝渗透率进行修正,使用裂缝的有效渗透率。
致密气藏的非达西流动对裂缝渗透率的影响可以表示为[17-18]:
(4)
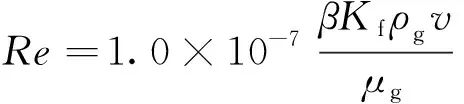
(5)
(6)
式中:Re为雷诺数;β为非达西流动系数,m-1;ρg为致密气密度,kg/m3;v为气体流速,m/s;μg为致密气黏度,mPa·s;φp为气藏孔隙度,%;a,b和c为常数。不同种类支撑剂a,b和c的取值[19]见表1。

表1 不同种类支撑剂a,b和c的取值
考虑气体非达西流动的有效渗透率公式为:
(7)
支撑剂指数修正为:
(8)
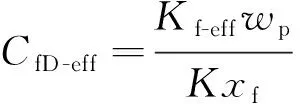
(9)
式中:CfD-eff为无因次裂缝有效导流能力;η为压裂液伤害系数。
2 致密气藏优化设计方法
2.1 修正后采气指数的计算
基于修正后的支撑剂指数,无因次采气指数JD的计算公式为[20]:
(10)
式中:re为泄气半径,m;f为函数。
式(6)与裂缝体积公式联立,可得:
(11)
(12)
式中:h为裂缝高度,m。
将式(11)带入式(10),整理得:
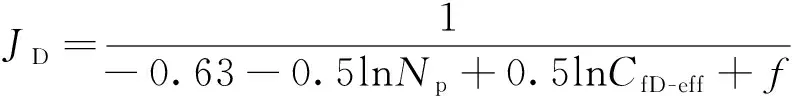
(13)
2.2 JD与CfD-eff的关系图版
Volko和Romero等人[21-23]运用直接边界元法计算了拟稳态下有限导流能力水力压裂的生产状况,并绘制了关系曲线。笔者在考虑有效导流能力和达西效应的基础上,考虑裂缝的拟表皮效应,得到了修正的一定支撑剂指数下采气指数和无因次裂缝有效导流能力关系图版(见图1和图2)。
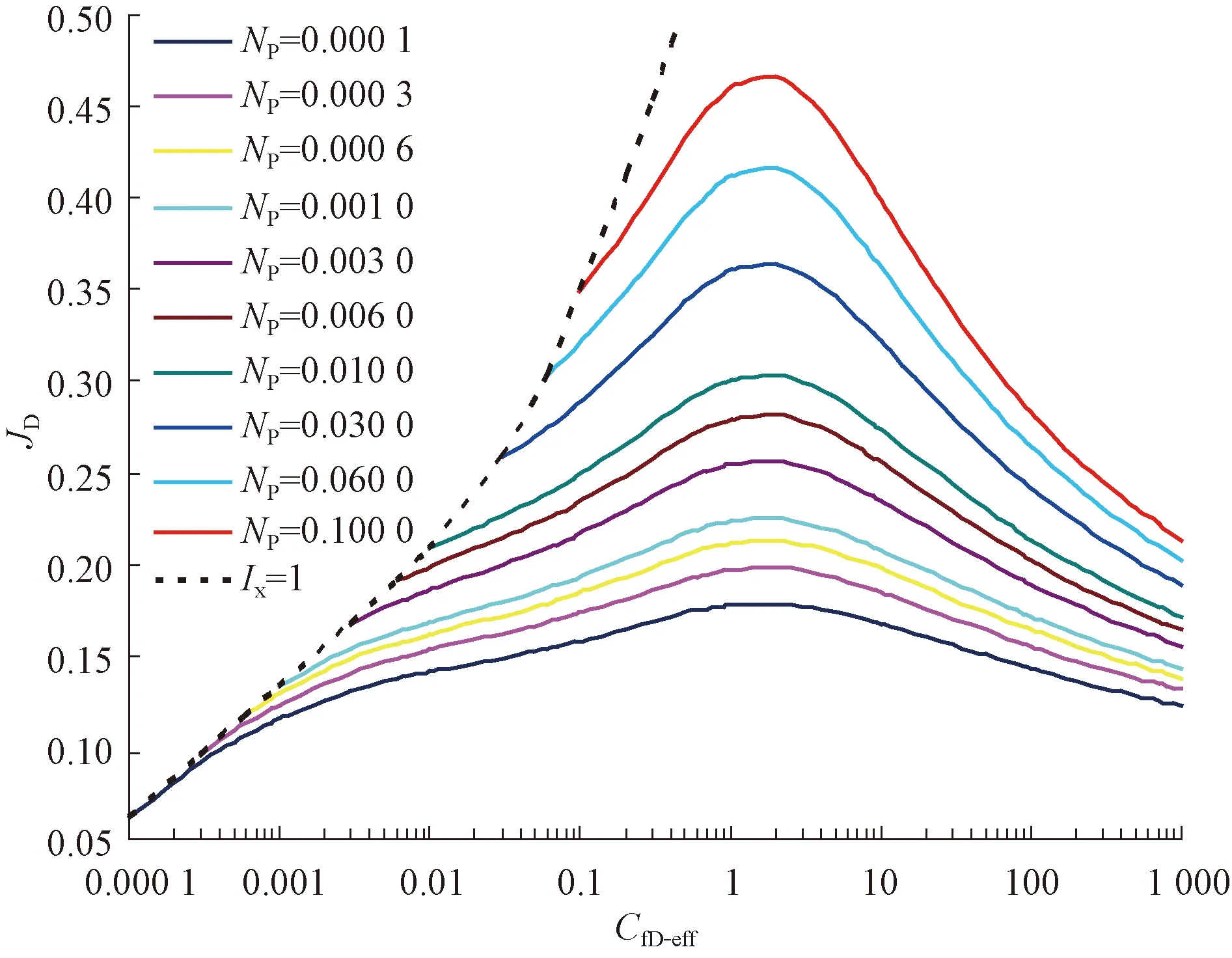
图1 Np≤0.1时JD与CfD-eff的关系Fig.1 Relationship between JD and CfD-eff when Np≤0.1
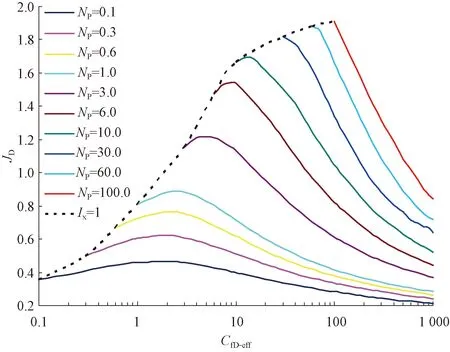
图2 Np>0.1时JD与CfD-eff的关系Fig.2 Relationship between JD and CfD-eff when Np>0.1
2.3 f函数
基于不同支撑剂指数下JD和CfD-eff的关系图版,拟合得到f函数如下:
1) 当Np≤0.1时
(13)
2) 当0.1≤Np≤1时
(14)
3) 当1≤Np≤10时
(15)
4) 当Np≥10时
f=4.058 5e-0.050 3u
(16)
其中u=lnCfD-eff
(17)
2.4 基于支撑剂指数的优化设计
1) 首先,根据支撑剂的种类、参数,压裂液破胶后对支撑剂渗透率的损害情况和邻井致密气非达西流动状况计算支撑剂有效渗透率;
2) 其次,根据储层参数,假设合理的支撑剂指数;
3) 若支撑剂指数的数值在JD与CfD-eff关系图版中能够查到,则根据图版选取该支撑剂指数下最优无因次裂缝有效导流能力;若查不到,则根据拟合出的f函数求得最优无因次裂缝有效导流能力,然后利用式(13)求得最大无因次采气指数;
4) 利用式(11)和式(12)计算裂缝的单翼缝长和缝宽,并与式(8)计算的单翼缝长相比较,如果两者接近,则计算的单翼缝长为最佳单翼缝长;
5) 如果相差较大,则重新假设支撑剂指数,重复上述步骤,直到单翼缝长的误差满足一定条件。
通过上述迭代便能得到对于特定致密气藏,在支撑剂性质一定的情况下,压裂施工所能实现的最优裂缝参数和最优导流能力,以及最大化的采气指数,对于致密气藏压裂施工具有指导作用。
3 实例应用
苏里格气田某致密气区块为400.00 m×400.00 m的方形井网,根据测井以及邻井资料获得的计算所需参数为:储层有效厚度20 m,渗透率0.1 mD;支撑剂为20/40目石英砂,其渗透率为60 000 mD;致密气的密度1.099 05 kg/m3,黏度0.028 3 mPa·s,渗流速度0.175 m/s;压裂液对储层的损害20%。
3.1 考虑非达西流动的影响
由式(6)求得非达西流动系数β=484 051.34 m-1,由式(3)求得雷诺数Re=3.914,根据式(7)计算出有效渗透率Kf-eff=13 543.64 mD。
假定Np=0.1,此时从图版上查得最优无因次裂缝导流能力CfD-eff=1.6,由式(11)计算得到xf=20.01 m,由式(8)求得xf=50 m,两者相差较大,不满足要求;需要重新选定Np进行计算,当Np的数值不在图版范围内时,通过f函数以及式(13)求得最优无因次裂缝导流能力;再利用式(8)和式(11)计算单翼缝长xf,直至两者计算结果的误差小于3%时停止。最终计算选定的Np=2.0,最优无因次裂缝导流能力CfD-eff=3.6,由式(11)计算得到xf=149.07 m,由式(8)计算得到xf=153.34 m,计算结果接近,所以单翼缝长xf=149.07 m,裂缝平均宽度wp=4.076 mm,最优无固次裂缝导流能力CfD-eff=3.6。
3.2 不考虑非达西流动的影响
计算过程如上,选定Np=9.8,最优无因次裂缝导流能力CfD-eff=10.05,由式(11)计算得到xf=193.17 m,由式(8)计算得到xf=197.497 m,计算结果接近,所以单翼缝长xf=193.17 m,裂缝平均宽度wp=3.236 mm,最优无因次裂缝导流能力CfD-eff=10.05。
从上面的计算结果可以看出,考虑致密气非达西流动对渗透率的影响后,最优裂缝参数的计算结果与不考虑时具有较大差异,支撑剂指数为不考虑致密气非达西流动时的1/5,有效导流能力为不考虑致密气非达西流动时的1/3,最优缝长缩短了1/5,最优缝宽增宽了1/4。致密气的非达西流动会降低有效渗透率,所以为了获得最大的采气指数和最优的导流能力,裂缝较没有损害时长度应缩短,宽度应增宽。
4 结 论
1) 引入了支撑剂指数的概念,既能体现压裂施工规模和气藏规模之间的关系,又能实现裂缝长度和裂缝导流能力之间的优化配置,对于气藏压裂优化设计具有重要作用。
2) 考虑致密气非达西流动对裂缝渗透率的影响,将裂缝有效渗透率引入到支撑剂指数中,修正了现有支撑剂指数的计算公式。实例计算表明,修正后求取的最优裂缝参数更加准确。
3) 利用边界元方法,考虑裂缝拟表皮效应以及压裂液破胶液和非达西流动对裂缝渗透率的影响,获得大量数据,做出在不同支撑剂指数下JD和CfD-eff的关系图版,能够清晰地表现出Np、JD和CfD-eff三者之间的对应关系,为致密气藏裂缝参数优化设计奠定基础。
4) 基于不同支撑剂指数下JD和CfD-eff的关系图版,拟合得到不同Np下考虑有效渗透率的f函数表达式,使考虑有效渗透率的JD计算有了明确的公式。
5) 基于修正后的支撑剂指数法对致密气藏裂缝参数进行优化设计,以采气指数为目标函数,在不同Np下JD和CfD-eff的关系图版基础上,运用迭代法寻求合适的Np以及相应的最优无因次裂缝导流能力,最终得到最优裂缝参数。
参考文献
References
[1] 李树松,段永刚,陈伟.中深致密气藏压裂水平井渗流特征[J].石油钻探技术,2006,34(5):65-69.
Li Shusong,Duan Yonggang,Chen Wei.Porous flow characteristics of fractured horizontal well in mid deep tight gas reservoir[J].Petroleum Drilling Techniques,2006,34(5):65-69.
[2] 张恒,刘洋,李强,等.水平井裸眼分段压裂完井技术在苏里格气田的应用[J].石油钻探技术,2011,39(4):77-80.
Zhang Heng,Liu Yang,Li Qiang,et al.Application of staged fracturing completion technology in horizontal openhole wells in Sulige Gas Field[J].Petroleum Drilling Techniques,2011,39(4):77-80.
[3] 曹阳,陈琛,史雪枝,等.川西致密气藏裸眼水平井分段压裂技术[J].石油钻探技术,2012,40(3):13-17.
Cao Yang,Chen Chen,Shi Xuezhi,et al.Multi-stage fracturing techniques for open hole horizontal wells in Western Sichuan tight gas reservoirs[J].Petroleum Drilling Techniques,2012,40(3):13-17.
[4] 任俊杰,郭平,彭松,等.非对称裂缝压裂气井稳态产能研究[J].石油钻探技术,2014,42(4):97-101.
Ren Junjie,Guo Ping,Peng Song,et al.Steady-state productivity for asymmetrically fractured gas wells[J].Petroleum Drilling Techniques,2014,42(4):97-101.
[5] 温庆志,王强.影响支撑剂长期导流能力的因素分析与探讨[J].内蒙古石油化工,2003,29(3):101-104.
Wen Qingzhi,Wang Qiang.Analysis and discussion of effective factors on sustaining longtime diversion ability[J].Inner Mongulia Petrochemical Industry,2003,29(3):101-104.
[6] 刘斌, 方行, 颜晋川,等.低渗致密气藏压裂过程中伤害实验研究[J].断块油气田,2009,16(1):81-82,104.
Liu Bin,Fang Xing,Yan Jinchuan,et al.Experimental study on fracturing damage in low permeability tight gas reservoir[J].Fault-Block Oil & Gas Field,2009,16(1):81-82,104.
[7] 马新仿,Valko Peter.裂缝非达西渗流对气井水力压裂设计的影响[J].油气地质与采收率,2010,17(5):83-85.
Ma Xinfang,Valko Peter.The effects of non-Darcy flow on design of hydraulically fractured gas well[J].Petroleum Geology and Recovery Efficiency,2010,17(5):83-85.
[8] 蒋廷学,王欣,王永辉.压裂优化设计方案的模糊决策方法及应用[J].石油钻采工艺,1997,19(4):74-76.
Jiang Tingxue,Wang Xin,Wang Yonghui.Fuzzy decision method and its application for well fracturing program optimization design[J].Oil Drilling & Production Technology,1997,19(4):74-76.
[9] 钟森.SF 气田水平井分段压裂关键参数优化设计[J].断块油气田,2013,20(4):525-529,534.
Zhong Sen.Key parameter optimization design of staged fracturing for horizontal well in SF Gas Field[J].Fault-Block Oil & Gas Field,2013,20(4):525-529,534.
[10] 曲占庆,黄德胜,李小龙,等.低渗气藏压裂水平井裂缝参数优化研究与应用[J].断块油气田,2014,21(4):486-491.
Qu Zhanqing,Huang Desheng,Li Xiaolong,et,al.Research and application of fracture parameter optimization of fractured horizontal well in low permeability gas reservoir[J].Fault-Block Oil and Gas Field,2014,21(4):486-491.
[11] Oligeny R,Economides M.Unified fracture design[M].Houston:Orsa Press,2002.
[12] Valko P P,Economides M J.Heavy crude production from shallow formations:long horizontal wells versus horizontal fractures[R].SPE 50421,1998.
[13] 金智荣,郭建春,赵金洲,等.复杂条件下支撑裂缝导流能力试验研究与分析[J].石油天然气学报,2007,29(3):284-287.
Jin Zhirong,Guo Jianchun,Zhao Jinzhou,et al.Experimental study and analyses on flow conductivity of fracture proppant under extreme conditions[J].Journal of Oil and Gas Technology,2007,29(3):284-287.
[14] 王雷,张士诚,张文宗,等.复合压裂不同粒径支撑剂组合长期导流能力实验研究[J].天然气工业,2005,25(9):64-66.
Wang Lei,Zhang Shicheng,Zhang Wenzong,et al.Experimental research on long-term conductivity of the proppant combination with different grain sizes in complex fracturing[J].Natural Gas Industry,2005,25(9):64-66.
[15] 卢聪,郭建春,王文耀,等.支撑剂嵌入及对裂缝导流能力损害的实验[J].天然气工业,2008,28(2):99-101.
Lu Cong,Guo Jianchun,Wang Wenyao,et al.Experimental research on proppant embedment and its damage to fractures conductivity[J].Natural Gas Industry,2008,28(2):99-101.
[16] Lopez-Hernandez H D,Valko P P,Pham T T.Optimum fracture treatment design minimizes the impact of non Darcy flow effects[R].SPE 90195,2004.
[17] Geertsma J.Estimating the coefficient of inertial resestance in fluid flow through porous media[J].Society of Petroleum Engineers Journal,1974,14(5):445-450.
[18] Cooke C E Jr.Conductivity of fracture proppants in multiple layers[J].JPT,1973,25(9):1101-1107.
[19] Penny G S,Jin Liang.The development of laboratory correlations showing the impact of multiphase flow,fluid,and proppant selection upon gas well productivity[R].SPE 30494,1995.
[20] Heber Cinco L,Samaniego F V,Dominguez A N.Transient pressure behavior for a well with a finite-conductivity vertical fracture[R].SPE 6014,1978.
[21] Valko P P,Doublet L E,Blasingame T A.Development and application of the multiwell productivity index(MPI)[R].SPE 51793,2000.
[22] Romero D J.Direct boundary method to calculate pseundo-steady-state productivity index of a fractured well with fracture face skin and choked skin[D].College Station:Texas A & M University,2001.
[23] Remero D J,Valko P P,Economides M J.The optimization of the productivity index and the fracture geometry of a stimulated well with fracture face and choke skins[R].SPE 73758,2002.
