k匿名数据上的聚集查询及其性质＊－

张君宝，刘国华，王碧颖，王 梅，王羽婷，石丹妮，翟红敏

（东华大学计算机科学与技术学院，上海201620）

1 引言

自Sweeney L提出k－匿名［1，2］以来，k－匿名隐私保护技术在国内外引起了广泛的关注。k－匿名有效预防了公开发布数据中隐私泄漏的问题，对包含隐私信息的数据共享做出了重大贡献。但是到目前为止，很少有人对k－匿名数据的知识发现进行研究，从k－匿名数据中获取有用的知识是目前亟待解决的问题。例如，在给定k－匿名病人信息表中，包含准标识符 Gender、Age、Zip－code、Area和敏感属性Disease、Expense。若能分别查出［10，20］、［20，30］等10个年龄段患癌症的人数，通过分析就可以得出年龄和患癌症之间的关系，通过统计不同地区患某种疾病的人数，可以判断“地区病”是否存在。k－匿名数据中大量地存在类似信息，对k－匿名数据的知识发现研究有重要的意义。

现有的不确定数据 OLAP［3～6］主要使用可能世界概率模型［7］对不确定数据聚集查询进行研究，时间效率很低。因为k－匿名数据的泛化程度很高，可能世界也要大得多，求解扩展数据库时间消耗限制了将不确定数据的聚集查询方法应用到k－匿名数据上的可能性。不确定数据OLAP最早由Burdick D等人于2005年在文献［3］中提出，在2007年，他们在文献［4］中对文献［3］的方法进行了补充；在同一年，文献［6］对元组间有约束的不确定数据OLAP进行了研究，基于元组间约束，构造约束超图，提出了新的扩展数据库分配策略。文献［5］给出了计算扩展数据库更加有效的分配策略。针对不确定数据的OLAP查询，研究者的技术路线是将不确定数据库展开成可能世界，然后为可能世界中的元组进行概率分配，将已经分配的可能世界合并得到扩展数据库，在扩展数据库上执行OLAP查询。其中概率分配算法是指数级时间复杂度，虽然文献［6］对算法进行了优化，但仍然是指数级的时间复杂度，查询的时间效率低。

文献［8～13］对不确定数据的聚集查询进行了研究，但仍是基于不确定数据概率模型，没有避免指数级的不确定可能世界展开。Jayram T S在文献［8］中将不确定数据转换为概率数据流，在此基础上研究了聚集查询的IO效率，给出了聚集查询的算法，并讨论了算法的时间效率和空间效率。Cormode G等人在文献［9］中给出了具有基数限制的不确定数据的关系操作实现算法，在此基础上给出聚集查询的实现，并对查询结果提供了两种处理方法，一种是求期望，另一种是求最大、最小值。Roy A在文献［10］中将不确定数据之间的相关性用层次超图来表示，基于层次超图给出了扩展数据库指数时间获取算法，并给出了聚集查询的实现。文献［13］给出了基于过滤策略的分布式聚集查询算法，将最不可能成为查询结果的数据删除，虽然该算法减少了分布式节点上的数据传输，但会导致信息损失。

文献［14～18］对隐私保护进行研究，但是没有人对k－匿名数据聚集查询进行研究。虽然文献［15］给出基于置换的匿名数据聚集查询方法，但该方法有很大的局限性，不能应用到k－匿名数据上。

总结上面的文献我们可以发现目前还没有有效的解决k－匿名数据知识发现的方法。为了解决k－匿名数据的知识发现问题，本文将研究重点放到k－匿名数据的聚集查询，并做出了以下贡献：

（1）给出k－匿名关系模式的定义：关系数据库在数据库领域占据着重要的位置，而关系模式是关系查询的基础。结合确定数据关系模式的定义，给出了k－匿名关系模式的定义。这对k－匿名数据使用关系数据库技术具有重要的意义。

（2）给出求解满足查询约束的值、概率序偶集合的算法，并将该集合作为第二阶段的输入：通过k－匿名数据不确定属性值的等概率特性，证明了k－匿名元组的可能世界实例的概率与其他元组无关。通过求解查询约束的析取范式，给出相对于析取范式中合取子式的独立属性集的概念。结合独立属性集，给出求解满足查询约束的值、概率序偶集合的算法。

（3）给出WITH子句约束定义及语义：针对不确定数据库，用户可能会提出不同的查询要求，例如查询年龄一定在［20，40］之间患癌症的人数，则年龄属性值为［30，50］的不确定元组不在查询结果中。为了满足用户这类需求，给出WITH子句约束的定义及其语义，并给出不同WITH子句约束对应查询重要性的概念。

（4）给出k－匿名聚集查询的性质：查询的性质对查询优化、用户选择合适的查询等具有重要意义。结合k－匿名聚集查询，给出不同 WITH子句约束聚集查询的单调性和一致性。

2 k－匿名模型

关系模式是关系数据库的基础，关系模式是对关系的准确描述。通过给出k－匿名的关系模式，为k－匿名数据应用可兼容的关系数据库理论打下基础。在给出k－匿名关系模式定义之前，先回顾一下确定数据关系模式中的经典定义。

（1）关系模式。

定义1 （基础域）基础域是一个无限常量的集合DOM。所有属性的属性值均属于DOM。

定义2 （关系模式）关系模式［19］R由以下两部分组成：

①有限字符串的集合U，称为属性集，用R［U］表示。R［U］中元素的个数称为元数，用arity（R）表示，即arity（R）＝｜R［U］｜。存在一个从R［U］到DOM的映射函数f，得到对应属性的属性域。

②R［U］上断言的集合Σ，Σ中的元素称为完整性约束。所有的关系实例都必须满足Σ。

（2）k－匿名关系模式。

k－匿名数据是满足k－匿名约束的特殊不确定数据，参考定义2并结合k－匿名的性质给出k－匿名关系模式相关定义。

定义3 （泛化域）基础域DOM 的幂集P（DOM）构成一个无限对象的集合GDOM，称为泛化域。GDOM中的元素称为泛化值。

泛化域是基础域的幂集，即泛化域中同时包含精确值和泛化值。例如，表1中Zip－code属性既包含泛化值“9021＊”，也包含精确值“07620”和“33109”。

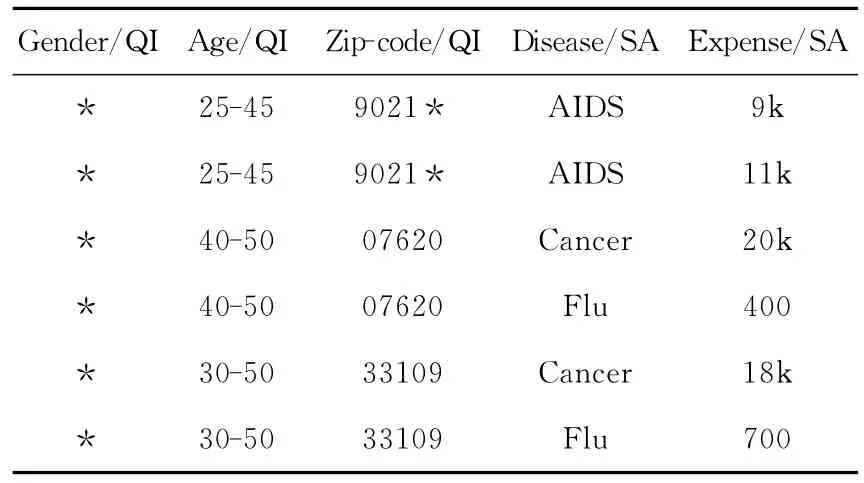
Table 1 2－anonymous table（DISEASE）表1 2－匿名表（DISEASE）

定义4 （k－匿名约束）给定R的任意实例I，I在准标识符［1］QI上的投影πQI（I），得到一个多重集MS。以MS中元素“相等”为一个等价关系，可将 MS划分为I1，I2，…，In共n 个等价类，其中，｜Ij｜≥k，1≤j≤n。

定义5 （k－匿名关系模式）k－匿名关系模式R是一个六元组R（U，GDOM，f′，QI，SA，Σ′），其中，

①U是一个有穷字符串集合，称为属性集。

②GDOM为泛化域。

③f′是一个从U到GDOM 的映射函数，称为域映射函数，值域对应各属性的属性域。

④QI为U的子集，称为准标识符。

⑤SA为U的子集，称为敏感属性集。QI∩SA＝Ø。

⑥Σ′是包含传统的完整性约束以及k－匿名约束的集合。

3 聚集查询

传统的关系数据库聚集查询将常量数值集合作为输入，通过聚集计算得到一个单一值作为输出。常用的聚集函数有SUM、COUNT、AVERAGE、MIN、MAX等。k－匿名数据的属性值为泛化值，泛化值中的每一个可能取值对应一个概率，不能简单地将满足查询条件的泛化值直接作为聚集函数的输入。一方面，k－匿名数据泛化值中只有一个是“正确”的；另一方面，泛化值的每一个可能取值均有可能是“正确的”，将满足查询约束的可能取值的期望作为返回值在一定程度上反映了真实查询结果。下面给出k－匿名聚集查询定义及其语义：

定义6 （聚集查询）给定k－匿名表T，T上的聚集查询形式化定义为AGGexp（δQC（T）），其中AGG为聚集函数名，exp为常量、属性或属性表达式。QC为查询条件，称为查询约束，δQC选择满足查询约束的元组实例。

QC是一个析取范式，若不满足，则使用现有的算法得到对应的析取范式。元组中的可能世界实例只要满足析取范式中任意合取子式，则这个实例在查询结果中，在后面只讨论QC为合取表达式的情况。虽然求解析取范式会花费一些时间，后面利用析取范式进行优化，弥补求解析取范式的时间消耗。

给定一个查询Q，满足Q中QC的所有元组构成一个区域，称为查询区域，表示为Region（Q），并且Regionatt（Q）⊆DOM。att为任意属性，Regionatt（Q）为Region（Q）在att上的投影。元组t的所有可能世界的集合构成一个区域，称为元组区域，表示为Region（t）。例如：元组〈［1，2］，3〉的元组区域为｛〈1，3〉，〈2，3〉｝。Region（t）在属性集 A上的投影称为A 属性区域，表示为RegionA（t），Region（Q）在A上的投影RegionA（Q）称为A属性查询区域。

在k－匿名表T上的聚集查询将满足QC的所有元组实例对应exp中属性值和对应的概率作为聚集函数的输入，然后通过线性运算得到查询结果。为了方便叙述，将查询过程分为两个阶段：（1）获得满足查询约束的元组实例对应exp中属性的属性值及其概率的集合。（2）在阶段（1）的结果集上进行线性计算得到最终查询结果。

3.1 聚集查询的第一阶段

性质1 （k－匿名数据元组实例概率分配的元组无关性）在k－匿名数据元组进行可能世界概率展开时，元组可能世界实例的概率与其他元组无关。

证明 k－匿名数据中不确定属性值的所有可能取值的概率相等，并且属性之间独立，元组之间独立。表2是一个任意的k－匿名表。根据k－匿名的不确定可能取值的等概率特性，元组1中的任意可能世界实例的概率为1／（｜Val11｜＊｜Val12｜＊…＊｜Val1m｜）＝Pr1，可能世界实例的个数为｜Val11｜＊｜Val12｜＊…＊｜Val1m｜＝Num1，Pr1＊Num1＝1。同样得到其它元组的可能世界实例的概率和个数分别为Pr2，Num2，…，Prn，Numn。将表2进行可能世界展开，则表2的所有可能世界中，任意可能世界实例的概率为Pr1＊Pr2＊…＊Prn，所有可能世界实例的个数为Num1＊Num2＊…＊Numn。元组1中的任意可能世界实例在表2的所有可能世界实例中的个数为Num2＊…＊Numn，所以元组1的一个可能世界实例的概率为：（Pr1＊Pr2＊…＊Prn）＊（Num2＊…＊Numn）＝Pr1，即元组1的可能世界实例概率只与元组1有关。同理可证其他元组可能世界实例的概率也只与元组本身有关。 □

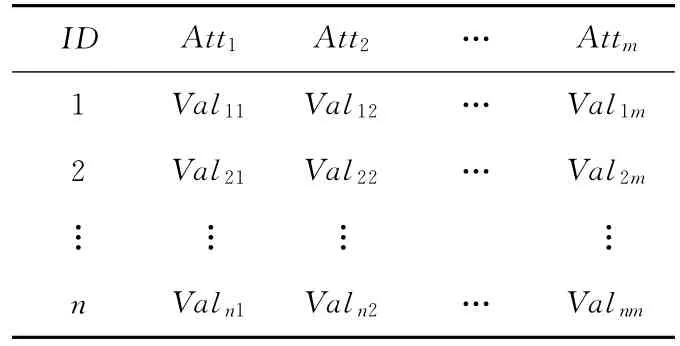
Table 2 Arbitrarily k－anonymous table表2 任意k－匿名表

例：给定表3的1－匿名表，对应展开的可能世界为｛〈1，3〉，〈3，3〉｝，｛〈1，3〉，〈3，4〉｝，｛〈1，3〉，〈3，5〉｝，｛〈2，3〉，〈3，3〉｝，｛〈2，3〉，〈3，4〉｝，｛〈2，3〉，〈3，5〉｝，表3的可能世界实例概率为（1／2＊1）＊（1＊1／3）＝1／6，进行可能世界合并后〈1，3〉的概率为1／6＊3＝1／2，与直接在元组1中进行分配的概率一致。

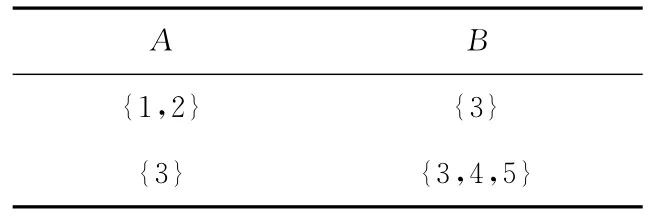
Table 3 1－anonymous table表3 1－匿名表

根据性质1，得到k－匿名数据中任意元组t的x）。通过该公式，在求解聚集查询的第一阶段，只需枚举元组独立属性集的可能世界。不在QC和exp中出现的独立属性集ATTy对应的QC（ATTy）＝ Ø，ATTy所有取值序列均在S 中，RegionATTy（t）满足QC（ATTy）的概率为1，只枚可能世界实例的概率为：1／｜Region（t）｜。遍历所有元组的全部可能世界实例，将满足QC的可能世界实例在exp中对应的属性上投影并结合该可能世界实例的概率得到聚集查询第一阶段的结果。遍历次数为｜Region（t1）｜＋｜Region（t2）｜＋…＋｜Region（tn）｜。k－匿名数据元组的可能世界较不确定数据要大得多，并且k－匿名数据存在大量的泛化数据。若将k－匿名数据的扩展数据库物化，需要的存储空间是｜Region（t1）｜＋｜Region（t2）｜＋…＋｜Region（tn）｜。否则，每次查询都枚举元组的可能世界实例，元组可能世界是相对于不确定属性个数的指数级。

给定k－匿名表T 和T 上的聚集查询AGGexp（δQC（T）），t为T 中的任意一条元组，Region（t）中满足QC的所有实例集合为S。若QC中的二元表达式包含两个属性A和B，则在S中A、B属性取值相关，用A relate B表示。将属性按relate求闭包，可以得到属性集U 的一个划分ATT1，…，ATTm，QC对应ATTi的约束为QC（ATTi），i∈［1，m］（若没有给出析取范式不存在对应关系）。t在ATTi上满足QC（ATTi）的可能取值序列集合为SATTi，则SATT1×…×SATTm一定在S中。即相对于S，ATTi和ATTj相互独立，i，j∈［1，m］，i≠j，ATTi为独立属性集。两个独立属性集的并仍然是一个独立属性集，当存在一个k－匿名关系实例，使独立属性集不能拆分为两个独立属性集时，称该独立属性集为最小独立属性集。relate闭包得到的独立属性集的属性之间相关，不相关的属性不会加入到闭包中，因此relate闭包得到的独立属性集为最小独立属性集。使用一般闭包算法就可得到相对于QC的最小独立属性集集合。

给定QC，得到满足QC的元组可能世界实例集合S的独立属性集为ATT1，…，ATTm。假设ATTx中包含exp 中的属性，RegionATTi（t）满足QC（ATTi）的个数为 Ni，i≠x，i∈［1，m］，那么RegionATTi（t）满 足 QC（ATTi）的 概 率 为 Ni／｜RegionATTi（t）｜，S在ATTx上的投影得到一个值序列的集合，集合中元素的概率为1／举在QC和exp中出现的独立属性集。

例：给定表T 中一条元组t为〈｛1，2，3｝，｛2，3，4｝，｛5｝〉，聚集查询为SUM2：（δ1：＞1and2：＞2（T）），对应QC1：＞1and 2：＞2的独立属性集集合为｛｛1：｝，｛2：｝｛3：｝｝。对应独立属性集｛1：｝满足QC（｛1：｝）的可能取值序列数目为2，｛2：｝中包含exp中属性，｛3：｝满足QC（｛3：｝）可能取值个数为1，所以对应｛2：｝中可能取值2、3、4的概率均为（1／3）＊（2＊1／3）＊（1＊1／1）＝2／9，与元组满足QC 可能世界实例在｛2：｝上的投影一致。其中｛2：｝满足QC（｛2：｝）的值序列为3和4，即将｛〈3，2／9〉，〈4，2／9〉｝作为第一阶段的结果。给定一条元组tuple、QC和exp，求元组满足QC的可能世界实例在exp中属性上投影及概率集合的算法，即求解聚集查询第一阶段结果的算法见算法1。

算法1 求解聚集查询第一阶段结果的算法

输入：k－匿名元组tuple、QC和exp；

输出：元组满足QC在包含exp的属性序列上的投影及对应的概率的集合。

Begin：

1.TmpPr＝1，Count＝0，resultSet＝Ø；

使用闭包算法，得到QC对应独立属性集的集合IS。

2.将IS中不包含QC和exp中属性的独立属性集删除，得到独立属性集集合IS′，IS′中元素个数为n，包含exp属性的独立属性集下标为x。

3.For：IS′中的每一个元素Ei，i≠x

Count＝0；

For：tuple在Ei上的每一个可能取值序列

If t满足QC（Ei）then

Count＋＋；

End if；

End for；

TmpPr＝TmpPr＊（Count／｜RegionEi（t）｜）；

4.End for；

5.For：tuple在Ex中每一个可能取值t

If t满足QC（Ex）then

将t在exp中属性上投影，其值为val，将〈val，TmpPr＊1／｜RegionEx（t）｜〉加入到resulSet中

（val值有重复）。

End if；

6.End for；

7.Return resultSet；

End

在聚集查询的第一阶段，用户可能会要求元组独立属性集中的每一个可能取值序列都必须满足QC中对应部分，或者属性值序列必须为精确值。例如，一个实力不足的投资公司对一个k-匿名个人信用信息表统计信用状况一定为“优秀”的人的特征，对满足统计特征的对象进行投资以减小投资风险。为了满足用户的这种需求，增加用户的查询能力，对k－匿名聚集查询增加WITH子句约束，该约束限制了属性查询区域与属性区域之间的关系。（详见第4节）

3.2 聚集查询的第二阶段

在第一阶段结束后，得到结果如表4所示。将表4的VAL代入exp中得到对应的值exp（VAL），exp 替换规则如下：（1）当 AGG 函数为SUM 或AVERAGE时，将exp中的属性名替换为对应的确定值。（2）当AGG为COUNT 时将exp替换成1或计算时默认为1但不进行替换，结果如表5所示。

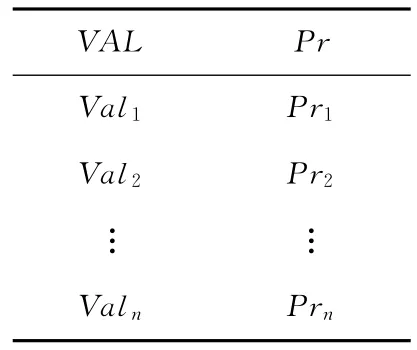
Table 4 Results table of aggregate query′s first stage表4 聚集查询第一阶段结果表

Table 5 Input table of aggregate function表5 聚集函数的输入表

将表5作为聚集函数的输入。给定聚集查询的输入，聚集函数的计算公式如下所示：

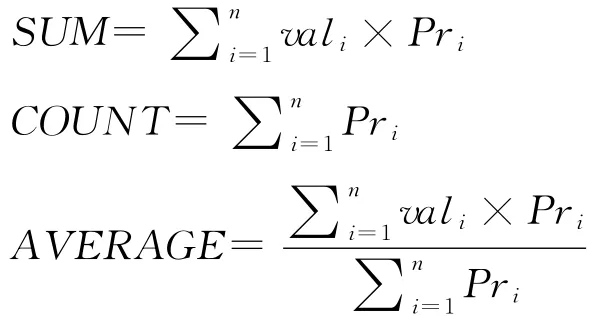
对于聚集函数MAX（MIN），可能出现满足查询条件的查询结果值是最大（小）的，但是对应的概率非常小，即该结果值出现的可能性很小，是否将该值作为查询结果返回给用户？这类问题是多因素最值选取问题。如何选取这类最值问题是Topk中研究的内容，在这里不进行讨论。

4 WITH子句约束

定义7 （WITH子句约束）给定查询约束QC，WITH子句约束原子 WCCA是一个谓词PWCCA（1，ATT），PWCCA（1，ATT）＝true。参数1的可选项为“CONTAIN”、“OVERLAP”、“NONE”；ATT相对于QC为独立属性集。WITH子句约束WCC是约束原子的谓词 PWCC（WCCA1θWCCA2θ…θWCCAn），θ∈｛∨，∧｝，PWCC＝true。

为方便描述，后面WCC默认只讨论包含一个WCCA的情况。其它情况类似。

图1中虚线矩形表示属性查询区域，实线矩形表示属性区域，显然无论什么情况第三类都不会在查询结果中，相同属性集上的不同OP约束互斥。结合图1，不同WCCA的语义定义如下：

PWCCA（NONE，ATT）：iff ATT 属性查询区域和ATT 属性区域对应的关系为类1，并且｜RegionATT（t）｜＝1，PWCCA为 true。PWCCA（CONTAIN，ATT）：iff ATT 属性查询区域和ATT 属性区域的关系为类1，PWCCA为true。PWCCA（OVERLAP，ATT）：iff ATT 属性查询区域和ATT属性区域的关系为类1或类2，PWCCA为true。

例：对表 1 查询 COUNT1（δAge≥40andAge≤50andDisease＝‘Cancer′（DISEASE））。若 用户给出WCC 为PWCCA（CONTAIN，Age），只有第3条元组WCC为true；若WCC为PWCCA（OVERLAP，Age），第3条和第5条的WCC 为true；若WCC 为PWCCA（NONE，Age），则没有元组使得WCC为true。

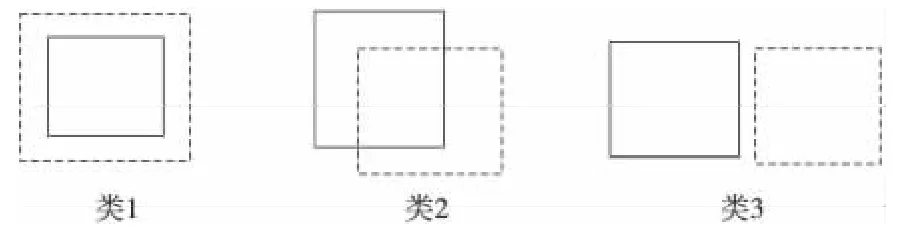
Figure 1 Relationship between query region and attribute region图1 属性查询区域与属性区域之间的关系

下面讨论WCCA满足的性质，通过该性质可以将WCCA中的独立属性集的并分解为最小独立属性集。

性质2 （WCCA一致性）给定一个WCCA为PWCCA（OP，AB），A、B 为属性集合。若A、B 相对于QC为独立属性集，则PWCCA（OP，AB）＝PWCCA（OP，A）∧PWCCA（OP，B）。即相对于QC，AB 的OP约束与A的OP约束和B的OP约束的合取保持一致。

证明 OP 选项可能为 “NONE”、“CONTAIN”、“OVERLAP”。当OP 为 NONE时，因为A和B独立，所以AB值序列在A和B上的投影也一定满足A 和B 的NONE选项；相反，A和B分别满足NONE选项，则笛卡尔积也一定满足NONE选项。同理可证其它OP也满足，证毕。

□

利用性质2，将ATT分解为最小独立属性集，在查询的第一阶段求解元组在独立属性集上满足QC对应部分的概率时，同时判断元组在此独立属性集上是否满足WCCA，若有一个独立属性集上的WCCA不满足，则WCC为假，元组不在查询结果中。

下面给出检查一条元组是否满足WCCA的算法。

算法2 给定查询约束QC，元组t，WCCA，判断t是否满足WCCA

输入：QC，t，WCCA；

输出：true，false。

Begin：

for WCCA中ATT的每个最小独立属性集A

If WCCA：1＝NONE and｜A｜＞1

return false；

Else if WCCA：1＝CONTAIN and ∃x∈Region

（A），QC（A）＝false

return false；

Else if WCCA：1＝OVERLAP and x∈Region

（A），QC（A）＝true

return false；

End if；

End for；

return true；

End

算法的每一次for循环只有一个if分支真正执行，每一个if判断的句子均可在O（n）时间内完成，n＝｜RegionA（t）｜，算法的时间复杂度为O（n）×m，m为ATT中最小独立属性集的个数。

定义8 （WCCA对应查询Q的重要性）任意给定表T和T上的聚集查询Q以及WCCA，WCCA的参数1分别使用选项OP1和OP2，对应满足QC和WCCA的元组数为Num1和Num2。若Num1≤ Num2（Num2≤ Num1）恒成立，则称OP1对应的查询Q的重要性比OP2弱（强）。

定理1 WCCA 分别使用 NONE、CONTAIN、OVERLAP选项时，对应WCCA的查询Q重要性逐渐增强。

证明 将定理2分为以下两部分：

（1）WCCA 分别使用NONE、CONTAIN选项时，对应WCC的查询Q重要性增强。

（2）WCCA 分别使用 CONTAIN、OVERLAP选项时，对应WCC的查询Q重要性增强。

证明（1）：由WCCA的不同选项对应的属性查询区域和属性区域之间的关系可知，在T中满足QC和WCCA的元组只可能存在两种情况：①元组同时满足两个WCCA。②元组只满足使用CONTAIN选项的WCCA。当只存在情况①时，Num1＝Num2；当只存在情况②时，Num1＜Num2；当两种情况都存在时，Num1＜Num2。根据定义8可知（1）成立。同理可证（2）成立，定理证毕。 □

5 聚集查询的性质

聚集查询的性质对查询优化、用户选择合适的查询等具有重要意义。例如，利用下面的单调性结合CONTAIN、OVERLAP的特点，我们可以得到真实数据统计结果的准确下限和近似上限。利用一致性，对数据进行划分，并发地执行查询，可以加快查询的响应速度。

5.1 单调性

定义9 （单调性）任意给定k－匿名表T 上的AGG聚集查询，相对于WCCA两个不同选项OP1和OP2，查询结果分别为q1、q2，若q1≥q2（q2≥q1）恒成立，则称AGG聚集查询满足单调性。

定理2 COUNT聚集查询满足单调性。

证明 假设T中满足QC和WCCA元组数分别为 Num1和 Num2，由定理 1，num1≥num2（num2≥num1）恒成立。COUNT查询结果与满足QC和WCCA的元组数成正比，因此q1≥q2（q2≥q1）恒成立。定理证毕。 □

由定理2的证明可知，当SUM聚集查询exp中属性域为正数时满足单调性，否则不满足单调性。AVERAGE聚集查询同时涉及到分子和分母，并不满足单调性。

5.2 一致性

定义10 （一致性）任意给定k－匿名表T 和AGG 聚集查询Q；T1，T2，T3，…，Tm是T 的一个划分，在T，T1，T2，T3，…，Tm上的聚集查询Q 的结果分别为q，q1，q2，q3，…，qm，若q＝AGG（q1，q2，…，qm），则称AGG聚集查询满足一致性。

定理3 SUM、COUNT聚集查询满足一致性。

证明 按照划分将k－匿名表中满足QC和WCCA 的所有元组排列为t1，1，t1，2，…，tm，n，则 Q在T 上的聚集查询结果为：Q（T）＝Q（t1，1，t1，2，…，tm，n）＝Q（t1，1，t1，2，…，t1，…）＋…＋Q（tm，1，…，tm，n）＝Q（T1）＋Q（T2）＋…＋Q（Tk），定理证毕。 □

对于AVERAGE聚集查询，k－匿名表T 的划分，满足QC和WCCA元组数目不同，为了使AVERAGE聚集查询满足一致性，将查询结果表示为〈Q（Ti），QNum（Ti）〉，QNum（Ti）为满足 QC 和WCCA 的 COUNT 结 果。AGG′（Q′（T1），Q′Q′（Ti）为〈Q（Ti），QNum（Ti）〉。

定理4 AVERAGE聚集查询AGG′操作下满足一致性。

根据AVERAGE聚集查询公式，定理4显然成立。 □

6 实验

实验环境是 Windows7 32bit操作系统，Intel T6600双核2.2GHz处理器，2GB内存，320GB 5 400r／min硬盘。底层数据库为 ORACLE11g。现有的k－匿名数据量小，不能在本实验中比较不同数据量及不同不确定数据百分比的时间及准确性。在实验中使用人工生成的确定数据，确定数据包含四个属性，将确定数据库的第二个属性当作准标识符。因为没有实现原型系统，为了在关系数据库上表示k－匿名属性值的不确定性，将属性值进行连续泛化，准标识符属性对应k－匿名表中两个属性，分别表示连续泛化的上限和下限，即确定数据对应的k－匿名数据有五个属性。k－匿名数据的k值和数据泛化的程度成正相关，在这里我们不讨论不同k值下的时间及准确性。下面对k－匿名数据聚集查询的时间效率和准确性进行实验验证。

6.1 查询的时间效率

查询的响应时间是用户体验的重要因素之一。现有的不确定数据聚集查询均是基于不确定数据库的可能世界展开，求解扩展数据库，然后在扩展数据库上执行查询。从文献［3］实验结果分析中可以看到，当不确定达到25%时获取扩展数据库的时间最高已经达到800秒以上，最少的也有200秒。扩展数据库上查询时间最高达到140秒以上，最少的也有10秒左右。k－匿名数据的不确定元组所占比例远高于25%，将不确定数据聚集查询的方法应用到k－匿名数据上，时间消耗会更高。本文研究的k－匿名数据聚集查询的时间效率远低于传统的不确定数据聚集查询方法。下面对查询的时间效率进行验证。从实验结果看，查询响应时间比较稳定，为多项式时间增长，同时查询的响应时间较不确定数据聚集查询方法效率要快很多，时间效率高。

图2～图4的实验中，WCC为作用在准标识符属性上的WCCA，数据量为50万条。从图2中可以看出，随着不确定数据量的增加，NONE选项的响应时间逐渐减小，因为NONE选项在遍历不确定属性的第二个可能取值时不满足WCCA，直接跳到下一个元组执行，大大减少了遍历不确定独立属性值的次数。从图3和图4可以看出，随着不确定元组所占比例的增加，查询响应时间成多项式时间增长，并且不同的聚集函数的查询响应时间相差不大。

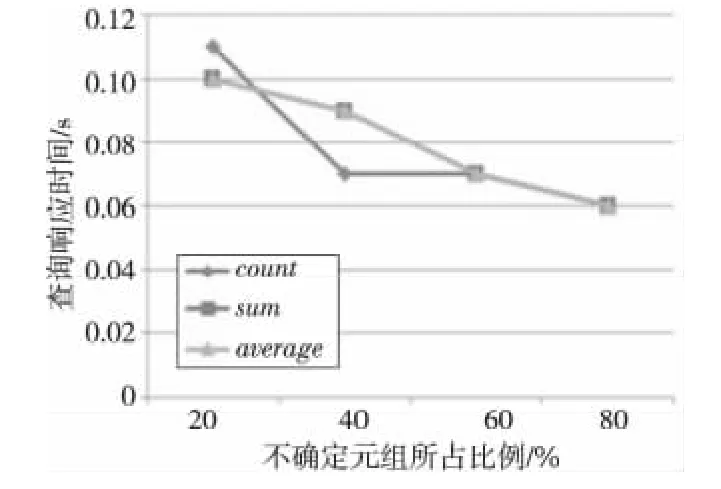
Figure 2 Query time of NONE option，500thousands tuples图2 NONE选项，50万条数据的查询时间

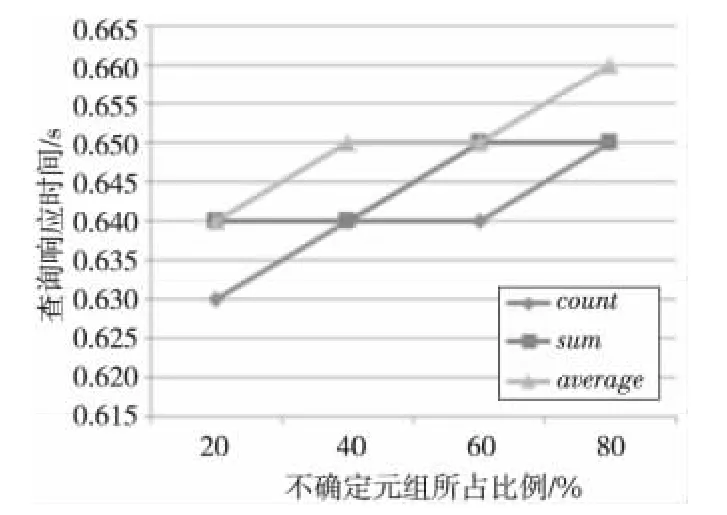
Figure 3 Query time of CONTAIN option，500thousands tuples图3 CONTAIN选项，50万条数据的查询时间

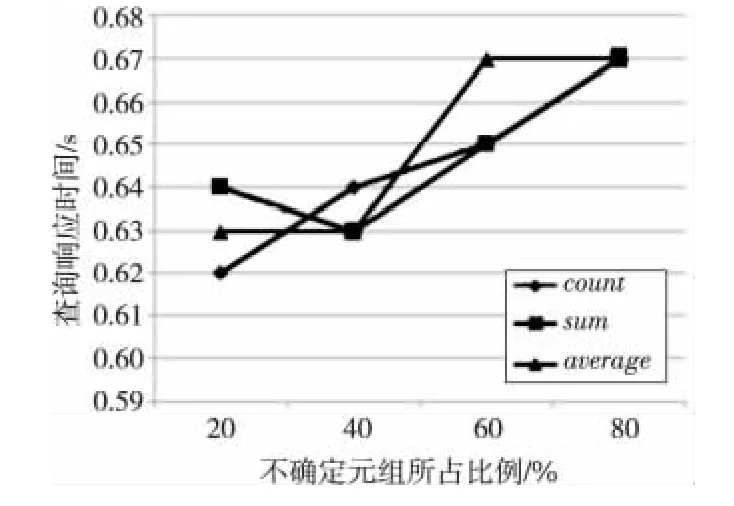
Figure 4 Query time of OVERLAP option，500thousands tuples图4 OVERLAP选项，50万条数据的查询时间

图5 ～图7的实验为不同数据量的查询响应时间。从图中可以看出随着数据量的增加，不同聚集函数的查询响应时间近似地成多项式时间增长，响应时间随着数据量的增长比较稳定。

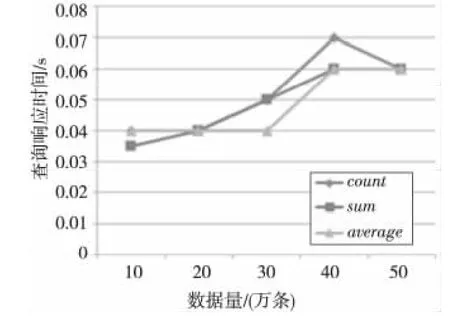
Figure 5 Query time of NONE option，80percent uncertainty图5 NONE选项，80%不确定数据的查询时间

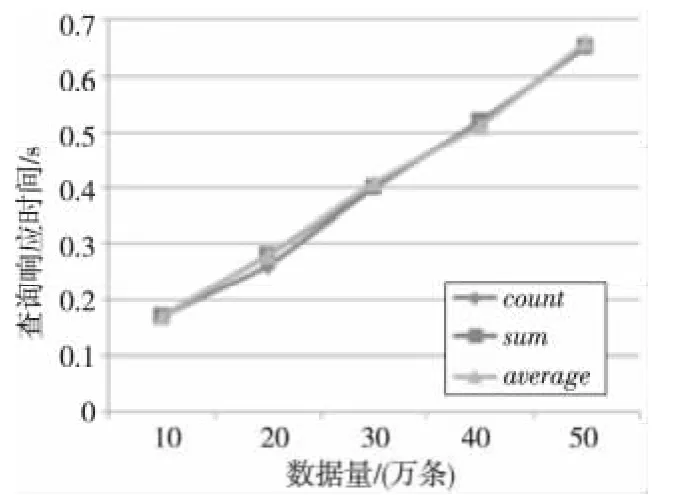
Figure 6 Query time of CONTAIN option，80percent uncertainty图6 CONTAIN选项，80%不确定数据的查询时间

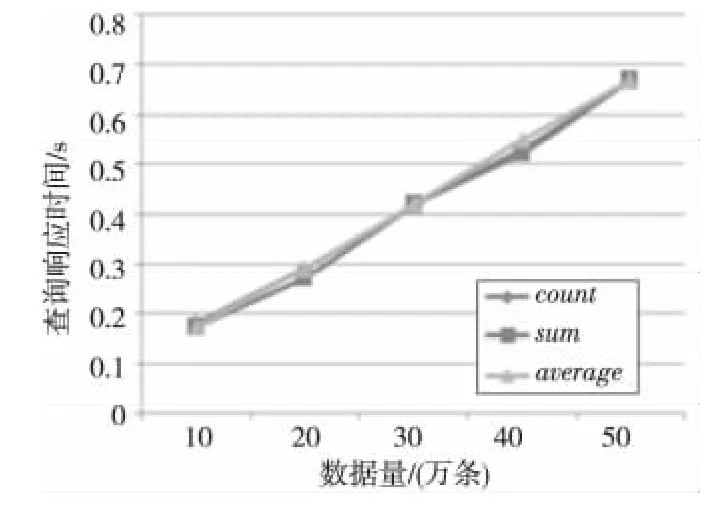
Figure 7 OVERLAP option，80percent uncertainty图7 OVERLAP选项，80%不确定数据

从图2～图7中可以看出，利用k－匿名的不确定数据可能取值的等概率特性，给出的多项式时间聚集查询的算法的时间效率非常高。在实验中没有加上求解析取范式以及两个属性之间相关的情况，但是在前文中提到当不确定属性值的个数有限时，聚集查询的算法仍为多项式时间的算法，时间同样满足多项式倍增长。

6.2 聚集查询的准确性

k－匿名数据中存在大量不确定数据。k－匿名数据的聚集查询结果与真实数据在大多数情况下不一致。现有的k－匿名算法保证了k－匿名数据的统计特征，使k－匿名数据的聚集查询在一定程度上反映原始数据的趋势。下面的实验对k－匿名数据聚集查询的准确性进行验证。

图8中查询为NONE选项，属性值为不确定的数据均不在查询结果中，所以不确定元组所占的比例越高，查询结果与真实值相差越多。AVERAGE聚集查询同时涉及分子和分母，随着查询结果中数据的减少，分子和分母同时减少，因此AVERAGE聚集查询结果的准确性没有随着不确定元组的增加产生剧烈变化。从前文中可以知道，NONE选项并不是为了返回与真实结果相近的结果，而是为了满足用户的特殊需求。

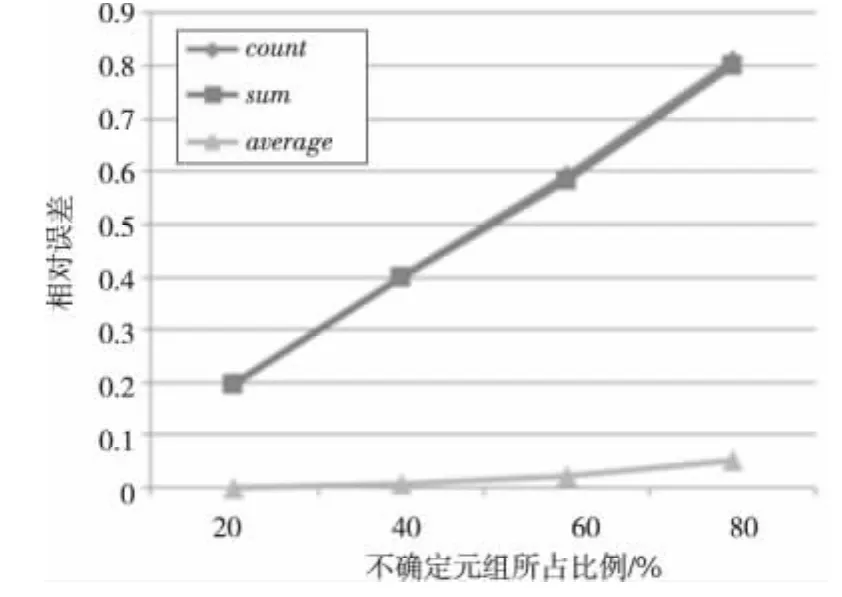
Figure 8 Relative error of NONE option，500thousands tuples图8 NONE选项，50万条数据的查询相对误差

从图9～图10可以看出，查询结果的准确性与不确定元组所占的比例不具有相关性，并且AVERAGE聚集查询结果的相对误差比较低。OVERLAP选项的查询结果较CONTAIN选项查询结果准确性要高。从整体上看，CONTAIN选项和OVERLAP选项的查询结果与真实值比较接近，查询结果的准确性较高。

从实验的时间效率和准确性两个方面看，本文的k－匿名数据聚集查询算法是有效的。

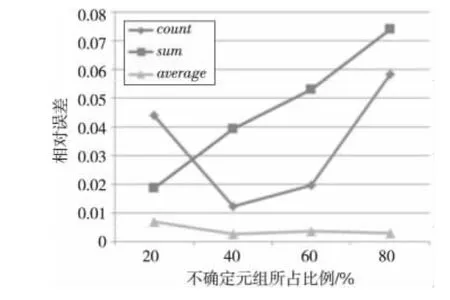
Figure 9 Relative error of CONTAIN option，500thousands tuples图9 CONTAIN选项，50万条数据的查询相对误差

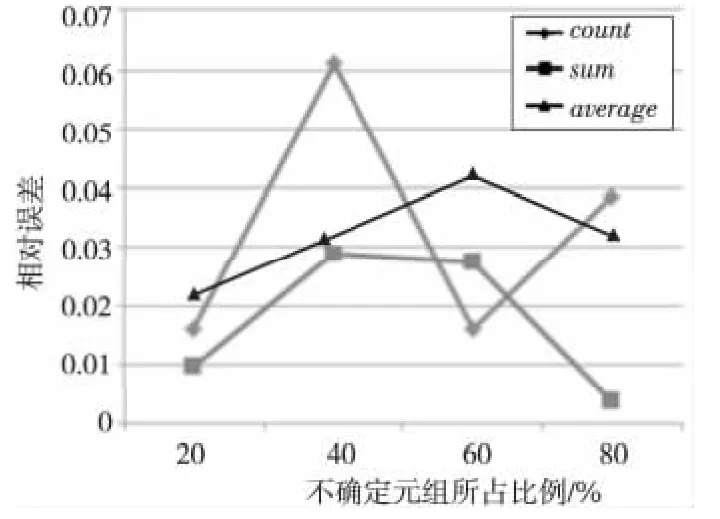
Figure 10 Relative error of OVERLAP option，500thousands tuples图10 OVERLAP选项，50万条数据的查询相对误差

7 结束语

本文给出了有效的k－匿名数据聚集查询方法，通过定义WITH子句约束，增加了查询的表达能力。对k－匿名数据的知识发现研究具有重要意义。

［1］ Samarati P，Sweeney L.Protecting privacy when disclosing information：k－anonymity and its enforcement through generalization and suppression［R］.Technical Report，SRI International，1998.

［2］ Samarati P.Protecting respondents’identities in microdata release［J］.IEEE Transactions on Knowledge and Data Engineering，2001，13（6）：1010－1027.

［3］ Burdick D，Deshpande P M，Jayram T S，et al.OLAP over uncertain and imprecise data［C］∥Proc of the 31st International Conference on Very Large Data Bases，2005：970－981.

［4］ Burdick D，Doan A H，Ramakrishnam R，et al.OLAP over imprecise data with domain constraints［C］∥Proc of the 33rd International Conference on Very Large Data Bases，2007：39－50.

［5］ Burdick D，Deshpande P M，Jayram T S，et al.Efficient allocation algorithms for OLAP over imprecise data［C］∥Proc of the 32nd International Conference on Very Large Data Ba－

ses，2006：391－402.

［6］ Burdick D，AnHai Doan，Ramakrishnan R，et al.OLAP over Imprecise data with domain constraints［C］∥Proc of the 33rd International Conference on Very Large Data Bases，2007：39－50.

［7］ Zhou Ao－ying，Jin Che－qing，Wang Guo－ren，et al.A survey on the management of uncertain data［J］.Chinese Journal of Computers，2009，32（1）：1－16.（in Chinese）

［8］ Jayram T S，Kale S，Vee E.Efficient aggregation algorithms for probabilistic data［C］∥Proc of the 18th Annual ACM－SIAM Symposium on Discrete Algorithms，2007：346－355.

［9］ Cormode G，Srivastava D，Shen E，et al.Aggregate query answering on possibilistic data with cardinality constraints［C］∥Proc of the 28th IEEE International Conference on Data Engineering，2012：258－269.

［10］ Roy A，Sarkar C，Angryk R A.Using taxonomies to perform aggregated querying over imprecise data［C］∥Proc of the 10th IEEE International Conference on Data Mining，2010：989－996.

［11］ Procopiuc C M，Srivastava D.Efficient table anonymization

for aggregate query answering［C］∥Proc of the 25th Inter

national Conference on Data Engineering，2009：1291－1294.［12］ Arbee L，Chen P，Chiu Jui－shang，et al.Evaluating aggregate operations over imprecise data［J］.IEEE Transactions on Knowledge Data Engineering，1996，8（2）：273－284.

［13］ Zhou Xun，Li Jian－zhong，Shi Sheng－fei.Distributed algorithms for aggregation queries over uncertain data［C］∥Proc of the 26th Chinese Conference on Database，2009：126－134.（in Chinese）

［14］ Rebollo－Monedero D，FornéJ，Pallarès E，et al.A modification of the Lloyd algorithm for k－anonymous quantization［J］.Information Sciences，2012，222：185－202.

［15］ Zhang Qing，Koudas N，Srivastava D，et al.Aggregate query answering on anonymized tables［C］∥Proc of the 23rd International Conference on Data Engineering，2007：116－125.

［16］ Jung E，Ahn S，Hwang S.k－ARQ：k－Anonymous ranking queries［C］∥Proc of the 15th International Conference，Database Systems for Advanced Applications，2010：414－428.

［17］ Martínez S，Sánchez D，Valls A.Towards k－anonymous nonnumerical data via semantic resampling［C］∥Proc of the 14th International Conference on Information Processing and Management of Uncertainty in Knowledge－Based Syst－em，2012：519－528.

［18］ Rebollo－Monedero D，FornéJ，Soriano M.An algorithm for k－anonymous microaggregation and clustering inspired by the design of distortion－optimized quantizers［J］.Data and Knowledge Engineering，2011，70（10）：892－921.

［19］ CalìA，Calvanese D，De Giacomo G，et al.Data integration under integrity constraints［C］∥Proc of the 14th International Conference，2002：262－279.

附中文参考文献：

［7］ 周傲英，金澈清，王国仁，等.不确定性数据管理技术研究综述［J］.计算机学报，2009，32（1）：1－16.

［13］ 周逊，李建中，石胜飞.不确定数据上聚集查询的分布式处理算法［C］∥第26届中国数据库学术会议论文集（A），2009：126－134.