基于增强条件公式的主动规则集可终止性判定＊

熊中敏，赵梦露，黄冬梅

（上海海洋大学信息学院，上海201306）

1 引言

由于集成有主动规则的数据库系统具有自动反应的功能，主动规则在SQL Server、Oracle、DB2和Informix等重要的商业数据库系统中得到了运用。主动规则近年来吸引了较多的关注，已经应用到许多新领域中：例如 XML 文档［1，2］、RDF［3］、语义网络［4］和传感器数据库［5］等等。遵循 Event－Condition－Action范型的主动规则之间的相互触发可导致整个规则集的无限次执行［6，7］，规则集的可终止性的判定成为一个难题［8］。为了限制触发器级联执行的深度，现有商业数据库系统采用门槛值的方法，比如Oracle定义该值为32。但是，定义合适的门槛值比较困难，定义过小，将误判可终止的规则集为不可终止，导致放弃已执行的正确结果；定义过大，真正的不可终止规则集被系统终止时已经循环执行多次，既浪费系统资源又使系统性能恶化。

为了克服已有判定方法的不足，本文提出了触发环的可执行序列概念，建立包含可更新变量的条件公式的方法和由此产生的规则集可终止性判定方法。分析结果表明，所提出的方法可以发现现有方法不能发现的可终止性情形。通过对主动规则集可终止性理论的研究，可为设计具有良好行为特性的主动规则集提供理论依据，并有助于设计并实现主动数据库系统的辅助分析工具，促进主动规则作为一种机制在其他行业中得到更多、更充分的应用。

2 相关知识

2.1 主动规则

主动规则常表示为 E－C－A 范型［7］，分别代表规则的触发事件、规则条件、规则的执行动作。ra和rb分别表示两个规则：（1）若ra的触发事件包含在rb的动作中，则称rb可触发ra；（2）若执行rb的动作可使ra的条件成立，则称rb可活化ra。这两种关系形成两种有向图：触发图（TG）和活化图（AG）。执行规则动作后因使自身条件不成立而无法再执行的规则称为自惰化规则。以上内容详见文献［7］。

2.2 规则执行模式

本文采取文献［9］中的规则处理过程，如图1所示。

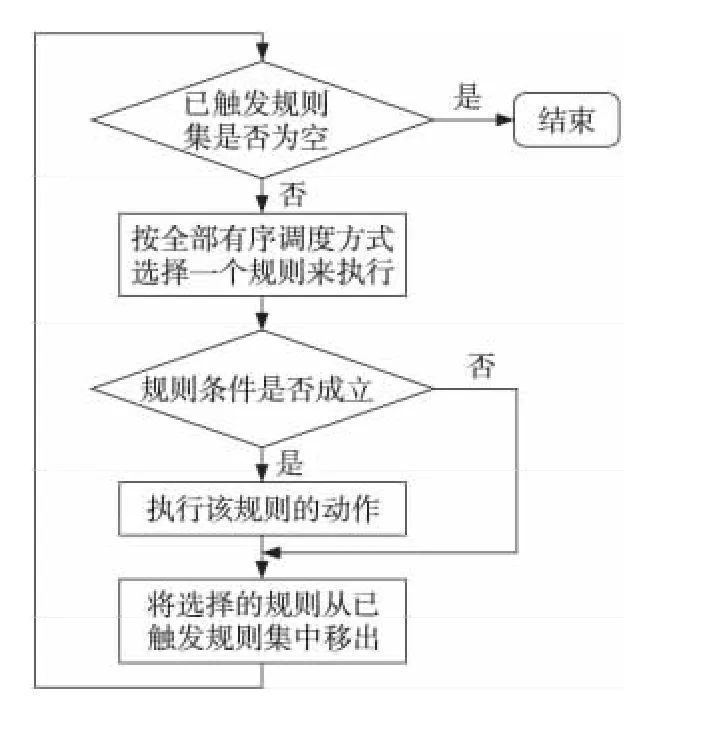
Figure 1 Process based on rule execution mode图1 基于规则执行模式的处理过程

2.3 相关研究分析

本文研究主动规则集在编译阶段的可终止性判定问题，该研究当前主要分为两类：基于触发图和活化图的方法和基于条件公式的方法。已有的研究工作都存在一定的局限。文献［10］通过分析主动规则集的语法建立触发图进行判定；文献［7］利用活化图进行判定，建立活化图的代数方法由文献［11］提出；本文的前期研究文献［12］根据规则的立即执行语义，提出触发环中规则同步执行的思想并用来建立不可归约规则集。虽然文献［12］将规则集分析细化到触发环分析，但这类方法都没有考虑触发环所有所属规则能否在同一次执行中执行，只是考虑单个规则在规则集或触发环的运行当中能否无限次执行。基于规则集或触发环建立条件公式的判定方法克服了这一缺陷。文献［10］提出移出边的方法，根据两个规则的条件建立条件公式；文献［13，14］提出移出路径的思想，考虑一个触发序列上所有规则条件建立更强的条件公式；本文前期工作文献［15］根据规则的立即执行语义，提出建立活化路径的条件公式进行判断的方法，能更大程度地解决包含有自惰化规则［7］的规则集的可终止性判定问题。但是，这类方法具有以下不足：（1）条件公式中只包含不可更新变量或有限次更新变量，而有限次更新变量的判定是一个NP问题［14］；（2）如果规则集只包含有限次执行的触发环，不能有效判断其终止性。下面通过一个实例说明上述已有判定方法的不足。

例1 图2以Oracle触发器方式定义如下的主动规则。

Figure 2 Related active rule set definitions图2 相关主动规则集定义

图3 表示上述规则集关联的触发图和活化图，其中虚线表示活化边，实线表示触发边。

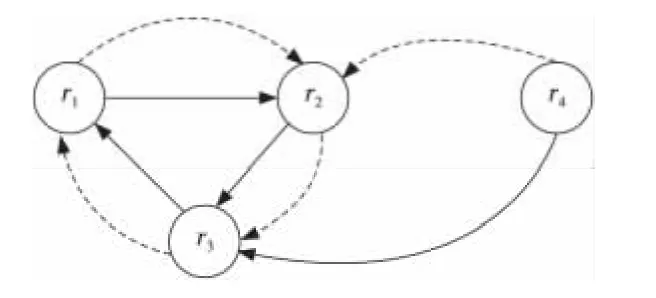
Figure 3 TG＆AG associated with rule set in Figure 2图3 与图2中规则集关联的TG图和AG图

图3 中一个 TG环R1｛r1，r2，r3｝和一个 AG环R′1｛r1，r2，r3｝，R1以执行序列r1r2r3r1循环触发执行。变量R.B、S.H、S.L、R.C 和R.D 既在R1的规则动作部分又在R1的规则条件部分，同时不出现在任何不属于R1但可由其触发可达的规则的动作部分。不属于R1但可由其触发可达的规则不能保证在R1的循环执行中真正运行。

（1）建立基于变量R.B的公式。R.B只在r1、r3的动作中赋予初值，由于公式中被更新变量应基于同一个初始值变化，所以有公式：δ1＝（R.B＝0），δ2＝（R.B ＝1）∧（R.B ＝1）＝ （R.B ＝1）。它们的真值为true，是可满足的。

（2）与变量R.B类似，建立基于变量S.H、R.C的公式：ξ1＝（S.H ＝1），ξ2＝（S.H ＝0），ξ3＝（R.C ＝1），ξ4＝（R.C ＝0）。它们的真值为true，是可满足的。

（3）建立基于变量R.D的公式。R.D被r3赋予初值，被r2更新，出现在r3的条件中。不妨将r3看作R1循环执行的第一个被触发规则，由于公式中被更新变量应基于同一个初始值变化，即R.D总代表一个初始值，所以如果R.D初值已被增量＋△L更新，则公式中包含R.D的条件谓词应将比较值以增量－△L更新，从而取得等价变换。建立的公式为：（R.D＜2－0.5）AND（R.D ＝1），真值为true，是可满足的。

（4）建立基于变量S.L的公式。R1中没有规则赋予S.L初值，S.L被r1更新，出现在r2的条件中。一旦r1再次作为被触发规则，R1完成一次循环执行，可建立以下公式：σ＝ （S.L ＝S.L ＋1）AND（S.L＜2）＝ （（S.L ＋1）＜2））。尽管当r4赋S.L初值0且σ＝true，R1可循环执行一次，但当R1循环执行到第三次，即S.L＝0，K＝2，使得σ＝ （（S.L＋K×1）＜2）＝false，导致r3不能真正被执行，R1必可终止。

图2中存在触发环，文献［6，10］不能判断此规则集可终止；利用文献［7，12］中的方法分析，只有r4从图2中移出，它们不能判断此规则集可终止；规则集中的变量都是可更新的，没有不可更新变量和有限次更新变量被文献［10，13～15］中的方法发现，它们不能判断此规则集可终止。

3 活化路径和活化路径集

为了表达规则之间的可无限次维持的活化关系，文献［15］提出了活化路径等概念。

定义1［15］若规则ri∈规则集R且有〈ri，rj〉∈TG，则称rj可由R直接触发可达；若rj可由R直接触发可达或存在规则rt可由R直接触发可达使得〈rt，rj〉∈TG，则称rj由R 触发可达。

定义2［15］若规则ri∈规则集R且有〈ri，rj〉∈AG，则称规则rj可由R直接活化可达；若rj可由R直接活化可达或存在规则ra可由R直接活化可达使得〈ra，rj〉∈AG，则称rj由R 活化可达。

定义3［15］r的一个活化规则表示为ra，与ra相关的r的活化路径Pa定义如下：（1）若ra∈一个活化环Ra，则Pa表示为Ra；（2）若ra∉一个活化环Ra但可由Ra活化可达，则Pa表示为Ra∪p′，p′满足下述特性：①ra可沿p′由Ra活化可达，但p′∉Ra中任一规则；②p′是极小化的，即p′上任一规则被消除，则属性①就不满足。

文献 ［7］已经证明从R的不可归约规则集中移出的规则必有限次执行。在后文中非特别说明，定理中所指的规则、TG环和AG环均包含在一个不可归约规则集中。

推论1［15］一个触发环RT中任意一个规则表示为r，若r总存在一条活化路径Pa且可由RT触发可达Pa中任一规则，则RT将具有非终止性；否则，RT必可终止。

4 基于活化路径建立条件公式

推论1没有考虑活化路径中的规则是否可以同时执行，其判断具有保守性。

定义4［15］触发环的规则执行序列 RES（Rule Execute Sequence）表示为：当触发环中至少一个规则被一个事务触发时，从r1到rn的循环执行，记作〈〈r1，…，rn〉〉＋，其中每个元素ri是互不相同的。属于触发环RT的所有RES，记作RESSet（RT）。

例2 在图3中，TG环R1｛r1，r2，r3｝具有两个RES：RES1＝〈〈r1，r2，r3〉〉＋，RES2＝〈〈r1，r2，r4，r3〉〉＋，RES－Set（R1）＝｛RES1，RES2｝。

定义5 规则r∈TG环RT且Pa为r的一条活化路径，δ为RT的一条执行序列，若满足特性：（1）δ包含Pa；（2）任一规则移出δ，则属性（1）不成立或RT上有一个规则不能被触发。则称δ相对于Pa是极小化的。

以下的调整操作保证RES－Set（RT）中RES相对于Pa是极小化的。

定义6 TG环RT的一条RES表示为δ，RT上一个规则的活化路径表示为Pa，定义操作Curtail（δ，RT，Pa）如下：若在δ上子序列P 满足如下性质：（1）P的起点A∉RT但A∈Pa；（2）P 的终点B∈RT；（3）r表示P 上除了起点A 和终点B之外的点，则r∉RT且r∉Pa。则起点A和终点B保留在P上，余下的点裁剪掉。

定理1 若规则r不属于TG环RT并且不能为其触发可达，则r不能与RT同步运行。

证明 通过反证法证明。假设r在RT上规则r′之后得到运行，根据前述的规则执行语义，必有r′触发r。根据定义1可知：r可由RT触发可达，与定理的前提产生矛盾，假设不成立，定理成立。 □

若r不属于RT但可由其触发可达，不能保证r能和RT同步执行，为判断RT的终止性建立的条件公式中的变量不应被r的动作更新；否则，无法明确评估此变量在RT的循环执行中的更新变化。根据定理1，提出以下定义。

定义7 若变量X出现在TG环RT的规则条件部分，但不出现在属于RT的规则或不属于RT但可由其触发可达的规则的动作部分，则称X为RT的不可更新变量。

定义8 若变量X同时出现在TG环RT的规则条件部分和动作部分，但不出现在不属于RT却可由其触发可达的规则的动作部分，则称X为RT的可更新变量。

由于公式中可更新变量应基于同一个初始值变化，而变量常常多次赋初值，故提出以下定义。

定义9 在TG环RT中，若规则r给一个可更新变量X赋初值，则r称为X的一个断点。

4.1 基于不可更新变量建立条件公式

根据定义7，基于不可更新变量X建立的条件公式为TG环RT中规则条件部分包含X的谓词的逻辑组合。详细方法见文献［13，14］。

4.2 基于可更新变量建立条件公式

在条件公式中，所有谓词中同一个可更新变量都是基于同样的初始值，初始值由其断点规则赋值，如果某个谓词中变量已发生增量＋△X的更新，变量始终看作其初始值，则应将比较值以增量－△X更新，并称这种等价变换为相对于断点规则的更新投影。

（1）如果触发环RT的可更新变量X在RT的执行序列ξ中无断点，则任选ξ中规则r为首个被触发规则，对其后执行规则中包含X的条件谓词做相对于r的更新投影，只能建立一个公式；

（2）如果触发环RT的可更新变量X在R的执行序列ξ中有断点r，则将r选为首个被触发规则，对其后执行规则中包含X的条件谓词作相对于r的更新投影，建立一个公式。

基于可更新变量建立条件公式的算法如算法1所示。

算法1 Formula－constructing

输入：TG环RT的执行序列ξ和RT的可更新变量X；

输出：条件公式集SC。

Begin

SC：＝Ø

（1）IF X 在ξ中无断点规则

r表示ξ中任一规则并作为其循环执行的首个触发规则；P表示r的条件中包含X的一个谓词；δ1表示首个建立的公式；Updated（X）表示在X上已完成的一组更新；δ1：＝P；

IF r的动作以＋△X更新X

Updated（X）＝｛－△X｝；

ENDIF

IF r的动作以－△X更新X

Updated（X）＝｛＋△X｝；

ENDIF

ENDIF

IF X在ξ中有多个断点

r表示X的任意断点规则并选作ξ循环执行中首个触发规则；P表示r的动作中赋X 初值的谓词；

δ1：＝ P；Updated（X）＝Ø；

ENDIF

（2）r′表示ξ的循环执行中下一个触发规则；

IF r′的条件中有形如X compare n 的谓词P／＊compare表示 “＞，＜”等比较符，n表示常数＊／

FOR∀deltax∈Updated（X）Do

n：＝n＋deltax；

ENDFOR

δ1：＝δ1∧P；

ENDIF

IF r′不为r且不是X 在ξ中的断点

IF r′的动作以＋△X更新X

Updated（X）＝Updated（X）∪｛－△X｝；

ENDIF

IF r′的动作以－△X更新X

Updated（X）＝Updated（X）∪｛＋△X｝；

ENDIF

Goto（2）

ENDIF

IF r′不为r但作为X 在ξ中的断点

SC：＝SC∪｛δ1｝；P′ 表示r′的动作中赋X 初值的谓词；

δ2：＝ P′；Updated（X）＝Ø；Goto（2）

ENDIF

IF r′即为r／＊ξ完成一次循环执行＊／

δn表示当前建立的公式；SC：＝SC∪｛δn｝；

Return（SC）；

ENDIF

END

5 TG环的可终止性分析

ρ表示TG环RT的一个规则执行序列，Formula（ρ）表示利用算法1和文献［13，14］中方法分别基于RT的可更新变量和不可更新变量为ρ建立的一组条件公式。

定理2 r表示一个TG环RT中的任意一个规则，若r总存在一个有效活化路径Pa且Pa中任一规则可由RT触发可达，同时RT满足如下性质：若∃ρ∈RES－Set（RT），满足Rules－Set（ρ）⊇Rules－Set（Pa）且∀δ∈Formula（Curtail（ρ，RT，Pa）），有δ≠false，则RT将具有非终止性；否则，RT必可终止。

证明 由定义5、定义6可知：对RES－Set（RT）中任意执行序列ρ，若都存在一个条件公式σ∈Formula（Curtail（ρ，RT，Pa）），有σ＝false，则RT或Pa上必有一个规则不能在ρ的循环中运行。这导致RT上必有一个规则因条件不满足或自惰化规则r的条件不能被Pa再次活化而不能真正运行，从而导致执行序列ρ不能循环运行而终止，即RT必可终止。反之，因为条件公式都能满足，Pa上所有规则和r都能被RT的一个执行序列ρ包含并与其同步循环执行，并且r能够在自惰化后被Pa活化，即ρ可循环运行，故RT将具有非终止性。 □

定义10 在TG环RT中，若可更新变量X在RT中没有断点规则，则X是RT的可累积更新变量。

如果X是RT的可累积更新变量，通过算法1只能为其建立一个条件公式，Sum（△X）表示RT按某一执行序列循环执行过程中对X产生的所有更新累积后的净效果。

定理3 X表示TG环RT的可累积更新变量，δ（X）表示通过算法1为RT的执行序列ρ建立的一个基于X 的条件公式，δ（X＋k×Sum（△X））表示当ρ循环执行k次，X产生可累积更新后δ（X）的表现形式。如果δ（X＋k×Sum（△X））＝false，则ρ必可终止。

证明 假设由算法1为RT的执行序列ρ建立的基于不可更新变量、可更新变量的所有条件公式都可满足，并按定理2判断RT将具有非终止性，可按ρ循环执行。在循环执行到第（k＋1）次时，经过ρ的k次循环过程中累积的更新后，X改变为（X＋k×Sum（△X））。如果通过算法1建立的公式δ（X＋k×Sum（△X））＝false，则ρ的第（k＋1）次循环中至少有一个规则因为条件无法满足而不能运行，导致ρ必可终止。 □

设R表示任意不可归约规则集，ST＝｛RT｜RT为R中的TG环｝。TG环的可终止性分析算法如算法2所示。

算法2 Refined Termi－test

输入：R的TG环集ST；

输出： 如果判断可终止，返回true；否则，返回false。Begin

（1）FOR每个TG环RT∈ST

Sign：＝false；／／假设RT不是可终止的

FOR每个规则r∈Rules－Set（RT）

flag：＝true；／／假设r是可终止的

IF（∃Pa∈Path－Setact（r）满足Pa是活化路径且∀r′∈Rules－Set（Pa），r′由RT触发可达）

IF（∃ρa∈RES－Set（RT）满足ρ包含Pa且有：∀δ∈Formula（Curtail（ρ，RT，Pa）），δ≠false，同时RT不存在当ρ完成K 次循环后满足δ（X＋k×Sum（△X））＝false的可累积更新变量X）

flag：＝false；／／r可非终止运行

ENDIF

ENDIF

IF flag

Sign：＝true；break；／／RT是可终止的

ENDIF

ENDFOR

IF NOT（Sign）

Return（false）；／／R不是可终止的

ENDIF

ENDFOR

（2）Return（true）；／＊无不可终止TG环，R可终止运行＊／

END

定理4 算法2是正确的、可终止的。其时间复杂度为O（m×p2×n），其中m表示触发环的个数，p表示规则集R中的规则个数，n表示活化环个数。

证明 定理2、定理3保证了算法的正确性；因为不可归约规则集R中TG环个数、一个TG环的RES个数、AG环个数、主动规则的个数、规则的活化路径个数、一个TG环中不可更新变量和可更新变量的个数都是有限的，故算法2可自动终止。很明显，算法的时间复杂度由触发环RT的可终止性判定决定，即决定是否存在flag＝false。在最坏情况下m个触发环都需要被检验；每个触发环所包含的规则个数Rules－Set（RT）不超过规则集R中的规则个数p；在最坏情况下每个规则都能由任何活化环活化可达，p个规则可以最多有（p×n）个活化路径，将每个活化路径中规则的触发可达判定和与之相关的条件公式的检测看作是基本操作，则最内层的For语句最多可执行基本操作 （m×p×（p×n））次。故算法的时间复杂度为O（m×p2×n）。 □

6 结束语

现有方法在判断含有自惰化规则的规则集可终止性时存在不足，为此，本文提出了触发环的执行序列的概念，从而将触发环和规则的执行语义结合在一起；并进一步提出了触发环执行序列上的可更新变量、不可更新变量的概念，给出了建立包含可更新变量的条件公式的方法和由此产生的判断规则集可终止性的技巧；同时，还给出了运用该方法的判定定理及其相应的算法。

［1］ Bonifati A，Ceri S，Paraboschi S.Active rules for XML：A new paradigm for e－services［J］.VLDB Journal，2001，10（1）：39－47.

［2］ Bailey J，Poulovassilis A，Wood P T.An event－condition－action language for XML［C］∥Proc of WWW’02，2002：486－495.

［3］ Papamarkos G，Poulovassilis A，Wood P T.RDFTL：An event－condition－action language for RDF［C］∥Proc of the 3rd Web Dynamics Workshop at WWW’04，2004：223－248.

［4］ Papamarkos G，Poulovassilis A，Wood P T.Event－conditionaction rule language for the semantic web［C］∥Proc of Workshop on Semantic Web and Databases，2003：855－864.［5］ Zoumboulakis M，Roussos G，Poulovassilis A.Active rules for sensor databases［C］∥Proc of the 30th VLDB Conference，2004：98－103.

［6］ Aiken A，Hellerstein J，Widom J.Static analysis techniques for predicting the behavior of database production rules［J］.ACM Transactions on Database Systems，1995，20（1）：3－41.

［7］ Baralis E，Ceri S，Paraboschi S.Compile－time and runtime analysis of active behaviors［J］.IEEE Transactions on Knowledge and Data Engineering，1998，10（3）：353－370.

［8］ Bailey J，Dong Guo－zhu，Ramamohanarao K.On the decidability of the termination problem of active database system［J］.Theoretical Computer Science，2004，311 （1－3）：389－437.

［9］ Paton N W，Diaz O.Active database system［J］.ACM Computing Surveys，1999，31（1）：63－103.

［10］ Karadimce A P，Urban S D.Refined triggering graph：A logic－based approach to termination analysis in an active object－oriented database［C］∥Proc of International Conference on Data Engineering（ICDE），1996：1.

［11］ Baralis E，Widom J.An algebraic approach to static analysis of active database rules［J］.ACM Transactions on Database Systems，2000，25（3）：269－332.

［12］ Hao Zhong－xiao，Xiong Zhong－min.An efficient algorithm about computing an irreducible rule set in active database［J］.Journal of Computer Research and Development，2006，43（2）：281－287.（in Chinese）

［13］ Lee S Y，Ling T W.Refined termination decision in active databases［C］∥Proc of International Conference on Database and Expert Systems Applications，1997：182－191.

［14］ Lee S Y，Ling T W.A path removing technique for detecting trigger termination［C］∥Proc of International Conference on Extended Database Technology，1998：1.

［15］ Xiong Zhong－min，Hao Zhong－xiao.An approach to termination decision for a rule set based on activation path and conditional formula［J］.Journal of Computer Research and Development，2006，43（5）：901－907.（in Chinese）

附中文参考文献：

［11］ 郝忠孝，熊中敏.计算主动数据库中不可归约规则集的有效算法［J］.计算机研究与发展，2006，43（2）：281－287.

［15］ 熊中敏，郝忠孝.基于活化路径和条件公式的主动规则集可终止性判定方法［J］.计算机研究与发展，2006，43（5）：901－907.