基于样本特征加权的可能性模糊核聚类算法＊－

黄卫春，刘建林，熊李艳

（华东交通大学信息工程学院，江西 南昌330013）

1 引言

聚类分析是多元统计分析的一种，也是非监督模式识别的一个重要分支。聚类的目的是使得相似的样本之间的距离尽可能地小，而不相似的样本之间的距离尽可能地大。随着模糊集理论的提出和不断发展，模糊聚类分析已成为聚类分析研究的主流，其中以基于目标函数的模糊C－均值FCM（Fuzzy C－Means）算法理论最为完善，应用最为广泛。模糊C－均值聚类算法是一种基于划分的聚类方法，根据最小二乘原理，采用迭代方法优化目标函数，最终得到每个样本点的归属。如今FCM算法已被广泛地应用于模式识别、数据挖掘、图像处理等领域［1～4］。

经典的FCM算法对初始聚类中心较为敏感，易出现局部最优的情况，且算法不考虑各个特征重要度及不同样本对分类的影响。在实际应用中，聚类中心的选取会在一定程度上影响输出结果，且一些数据集的样本分布是非均匀的或非对称的，也就是说样本的特征对分类的结果是不均匀的，这些都会影响聚类效果。针对以上问题，许多学者提出了FCM的改进算法，如KPrishnapuranm K和Keller通过放松隶属度约束的限制提出了可能性C－均值算法PCM（Possibilistic C－Means）。Pal N R 等［5］把FCM算法中的隶属度和PCM算法中的可能性典型值相结合提出了可能性模糊C－均值算法PFCM（Possibilistic Fuzzy C－Means）。也有学者通过将遗传算法和模糊聚类算法相结合，提出了许多混合算法，如于水英等［6］提出了将遗传算法和模糊聚类相结合并应用到文本分类以提高分类效果；许松荣等［7］提出基于遗传算法的模糊聚类算法等。还有学者提出了一些基于权重的混合算法，如王丽娟等［8］提出的基于属性权重的FCM 算法；Shen Hong－bin等［9］提出的基于 mercer核的属性加权FCM方法；贺杨成等［10］提出的特征空间属性加权混合C－均值模糊核聚类算法；蔡静颖等［11］提出的基于马氏距离特征加权的模糊聚类新算法；刘兵等［12］提出的基于样本加权的可能性模糊聚类算法等。这些改进算法都在一定程度上解决了经典FCM的噪声敏感及局部最优的问题，但面对样本离群点或噪声数据较多时，算法性能可能会受到较大的影响。本文提出了一种基于样本－特征加权的可能性模糊核聚类算法，利用可能性聚类的思想解决了噪声敏感和一致性聚类的问题；同时，在聚类过程中动态计算样本属性特征间的不平衡性和样本对聚类的重要性的权重，减少噪声数据和例外点对聚类的影响，优化选取核参数并不断修正核函数把原始空间中非线性可分的数据集转化为高维特征空间中的可分数据集。实验结果表明，该算法能减少噪声数据和例外点的影响，比传统的聚类算法具有更好的聚类精度。

2 模糊C－均值聚类算法

设定一个具有N个样本的数据集X＝｛x1，x2，…，xN｝，xi＝ ｛xi1，xi2，…，xiL｝，i＝1，2，…，N ，每个样本点xi有L个属性，把其划分到c个不相交的数据集中，每个数据集的聚类中心分别为v1，v2，…，vc。FCM算法使用模糊划分，每个样本点xj被赋予一个属于第c个类别的隶属度值，隶属度值的取值范围为0～1。其目标函数如下：

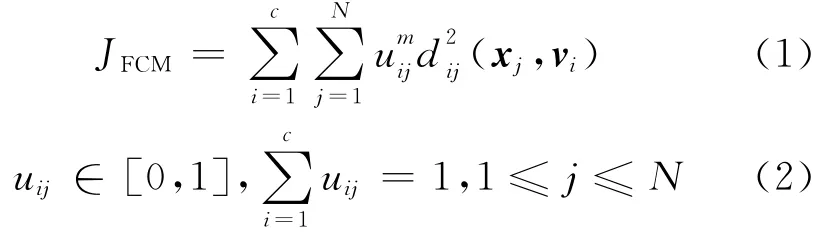
其中，dij为数据点xj与聚类中心vi的距离，在经典的FCM算法中总使用欧氏距离来计算；m为模糊指数，表示隶属度矩阵的模糊程度，在实际应用中m的最佳取值范围为 （1.5，2.5）。通过拉格朗日乘法来求解式（1）可得隶属度uij、聚类中心vi的迭代式：

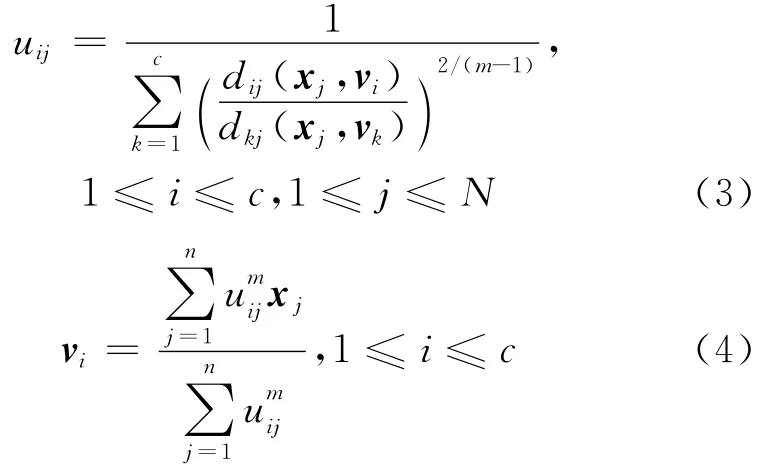
但是，经典的FCM算法本质属于局部搜索的爬山法，对初始聚类中心较为敏感，易出现局部最优的情况，且该算法不考虑各个属性特征及样本总体对分类重要性的影响。

3 基于样本－特征加权的可能性模糊核聚类算法

3.1 样本－特征加权

样本加权是为了克服离群点对聚类分析的影响，加快聚类的收敛速度。通过给每个样本整体添加一个权值，表示其对聚类的贡献程度。对噪声数据或例外点赋予一个较小的权值，使其参与聚类的程度被降低，也就减少甚至消除了它们对聚类结果的影响。假设样本集X＝ ｛x1，x2，…，xN｝，为每个样本xi赋予一个权重αj，αj的表达式如下：

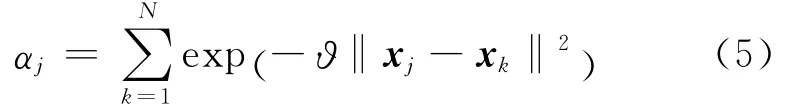
其中，ϑ为正的常数，j＝1，2，…，N ，‖xj－xk‖表示两个样本xj与xk之间的欧氏距离。

显然样本权值的大小与样本点到其它所有样本点之间的距离有关，离群点离样本的距离相对较远，那么其被赋予的权值就较小，也就减少了离群点的影响。同时，为了体现样本属性特征对类别的重要程度，定义一个权重系数wik，表示第k个属性对i类的重要性，且：

假定 为一非线性隐射函数，：RL→H，x→（x），其中x∈RL是原始空间的一个样本点，H为映射后的高维特征空间。把欧氏距离计算换成核函数计算，则基于样本－特征加权的可能性模糊核聚类算法的目标函数（简单表示为SFPFKM）为：

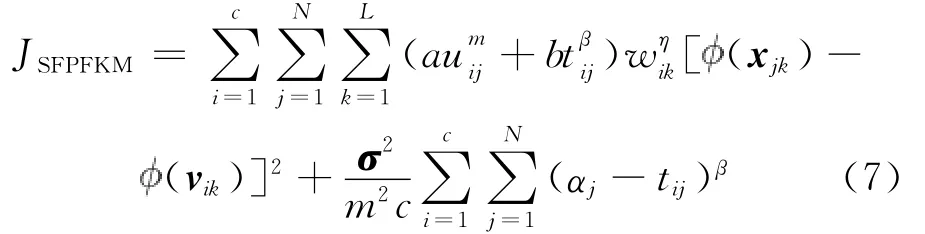
其中，1≤i≤c，1≤j≤N，c为类别数，vik是第i类的聚类中心，uij表示第j个样本属于第i类的隶属度，tij为第j个样本属于第i类的可能性，σ2是协方差矩阵，其计算方法［13］如下：

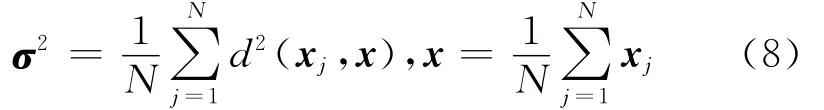
定义核映射函数为：

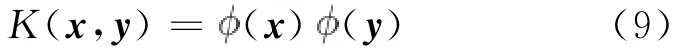
任何一个函数只要满足 Mercer定理［14］条件就可以作为Mercer核。用一个非线性函数 （x）把所有样本映射到高维空间，可以得到新的样本集。核的引入在原始空间中诱导出了依赖于核的新的距离度量。由式（9）可得：

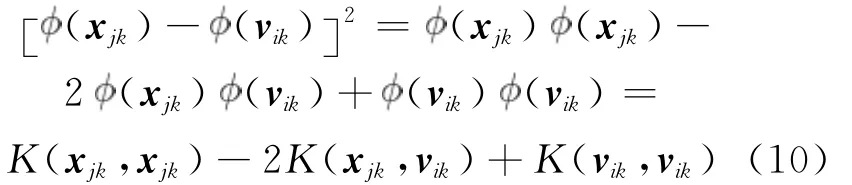
其中核函数为高斯核函数：

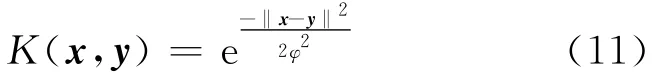
由式（10）可得 K（x，x）＝1，则式（7）经过转化可得：由式（12）的极值约束条件，根据拉格朗日乘法可得：

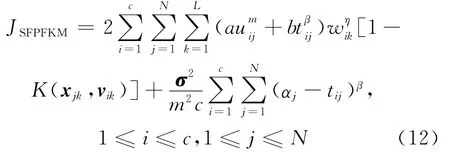
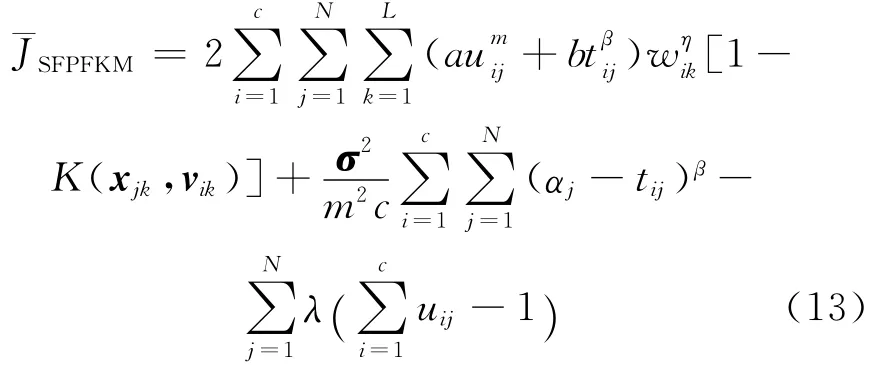
其中λ为拉格朗日系数，其最优化的一阶必要条件为：

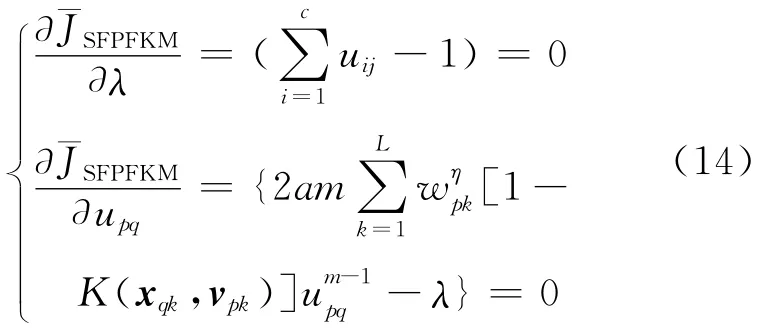
由式（14）可得隶属度uij的迭代式为：

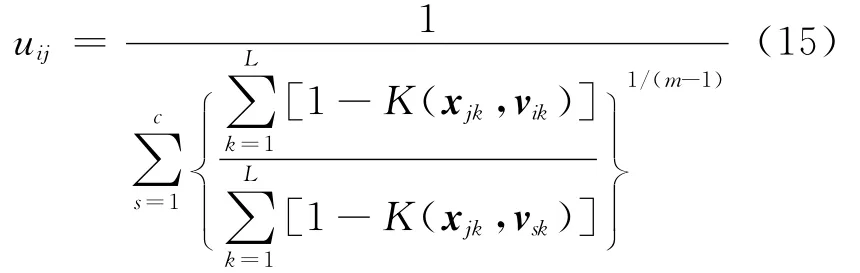
同理，由式（12）和式（13）可得权重系数wik、典型值tij和聚类中心vik的计算式分别为：

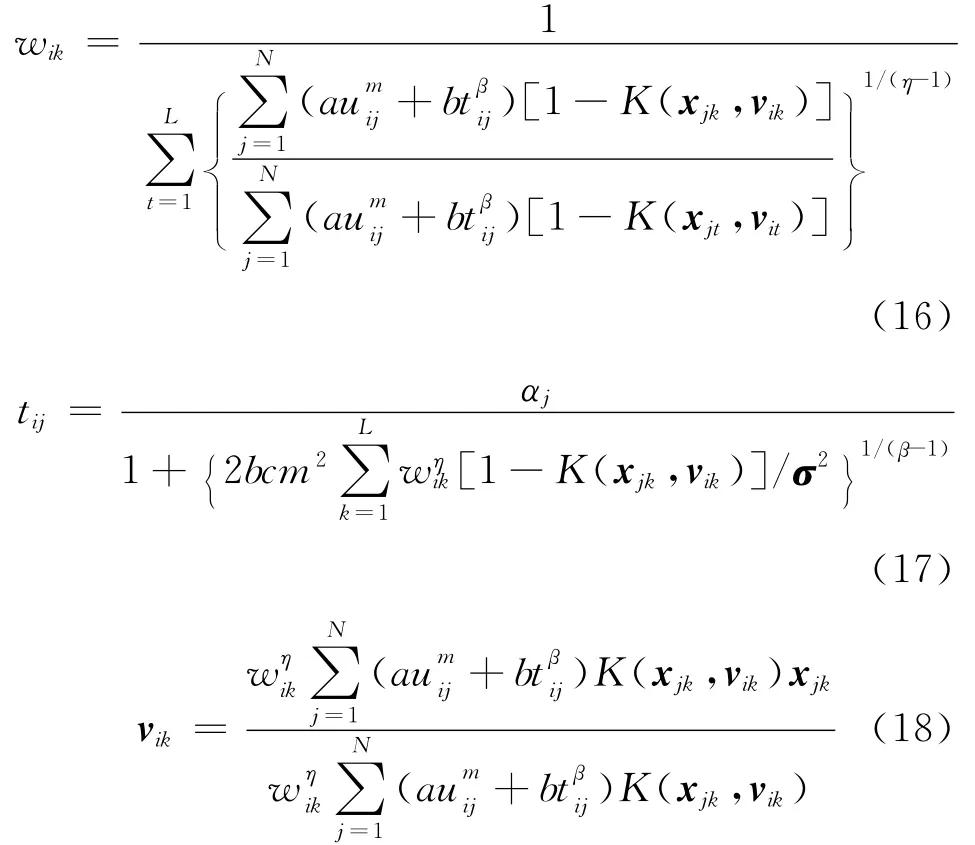
3.2 修正核函数及核参数优化

根据权重系数wik取值的不同，聚类中心vik的取值也不同，可得：

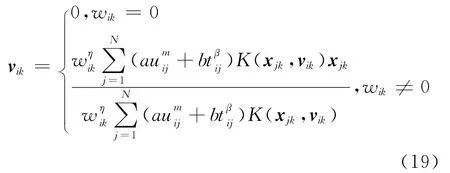
为了使目标函数获得最优解，需要合理选取核函数的核参数φ，比较典型的方法是通过下降梯度法和交叉验证法来确定φ的取值［15］。本文选用下降梯度法来确定φ的取值，φ的迭代式为：

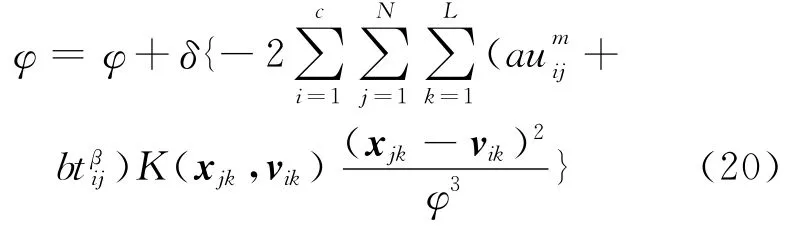
其中δ为迭代步长。

对于一个正标量函数D（x），定义：

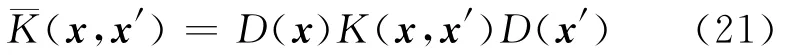
把式（12）称为核函数通过因子D（x）的保形变换。¯K（x，x′）为支持向量机的修正核函数［16］。

可以通过修正核函数来提高分类的精度，整个修正过程分为两步：第一步是利用原始核函数进行聚类以产生支持向量，第二步利用支持向量信息修正核函数。令：

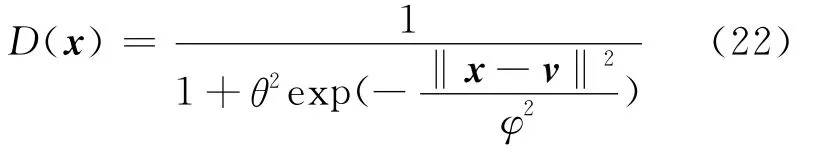
其中，θ为任意常数，v为聚类中心。由式（22）所得的修正核函数仍满足Mercer条件［17］。

φ的初始值［18］设为：

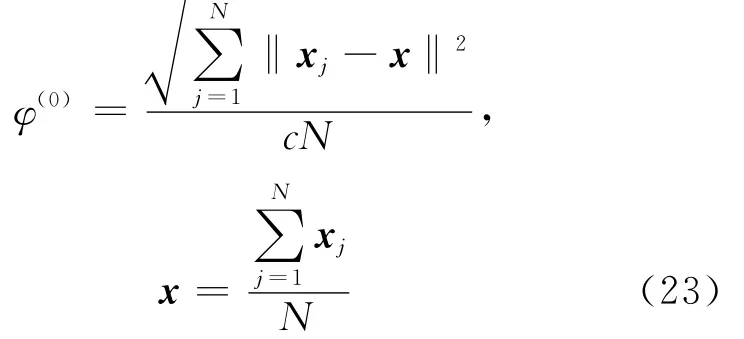
其中，c为聚类数，N为样本总数。

通过以上可得基于修正核函数的特征加权模糊核聚类算法，其描述如下：

步骤1 设定聚类数c，模糊权重指数m，核参数的迭代步长δ，ϑ＞0，a＞0，b＞0，β＞1，η＞1，最大迭代次数max＿t，算法停止时最小阈值ε＞0。

步骤2 运行FCM算法，并以其结果作为初始聚类中心矩阵v（0）、初始隶属度矩阵u（0）。

步骤3 随机初始化典型值t（0）、权重w（0），令t＝1。

步骤4 使用式（23）初始化核参数φ＝φ（0）。

深基坑施工是基础施工的基础，开工前根据建筑工程实际对基坑施工标准进行全面的优化，要确保基坑自身的强度及安全稳定性，增强地基的称在恶劣，并且施工人员也要严格的按照施工工序进行施工，确保深基坑施工的安全性。

步骤5 使用式（21）和式（22）不断修正K（xj，vi），并使用如下迭代公式进行循环，逼近最优解：

（1）使用式（18）更新聚类中心v（t）；

（2）使用式（17）更新典型值t（t）；

（3）使用式（16）更新权重值w（t）；

（4）使用式（20）计算新的核参数φ（t）；

（5）使用式（15）更新隶属度u（t）；

（6）t＝t＋1；

4 实验结果与分析

为了验证本文算法的鲁棒性和有效性，利用从UCI中选取的四个数据集和含噪声数据集两组实验对算法进行验证。在实验中将本文算法的聚类性能分别与FCM算法、PCM算法、PFCM算法的性能进行对比。在UCI中的四个数据集上比较各算法的聚类精度，也就是正确聚类样本数与样本总数所得的比值，值越大也就是聚类的精度越大，正确聚类的样本越多；在含噪声数据集上比较算法发现含噪声数据的聚类中心的能力。算法在PC机上利用 Microsoft Visual C＋＋6.0进行仿真实验。

4.1 UCI数据集实验

从UCI中选取的四个数据集分别为Iris、Wine、Pima和 Breast－cancer，这四个数据集是比较无监督聚类效果好坏的典型数据，其基本特征如表1所示，将这四个数据集应用不同算法的聚类结果如表2所示。

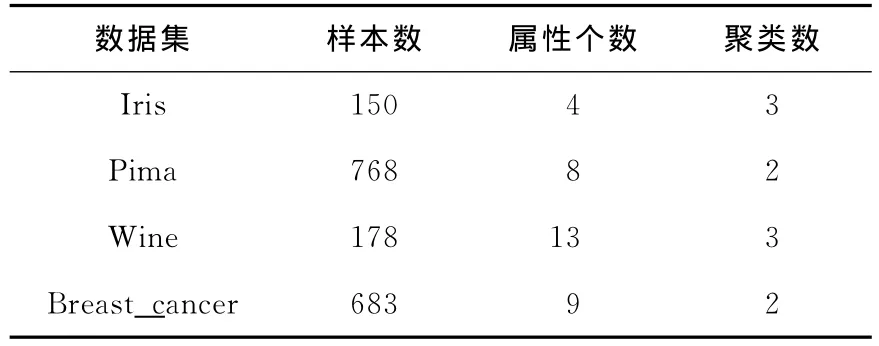
Table 1 Basic information of data set表1 数据集的基本信息

实验中各参数的配置为：ε＝0.000 01，最大迭代次数max＿t＝150，m＝2.0。PFCM 算法在四个数据集上的其它参数设置为a＝1.0，b＝1.0，β＝2.0；本文算法在四个数据集上的其它参数分别设为a＝1.0，b＝1.0，β＝2.0，η＝2.0；a＝1.0，b＝50，β＝1.5，η＝2.0；a＝0.1，b＝100，β＝1.5，η＝2.0；a＝0.1，b＝90，β＝1.0，η＝2.0（这些参数的选择是根据多次实验而来的，为方便比较，我们选取具有最优的聚类效果的参数作为本文算法的实验参数）。

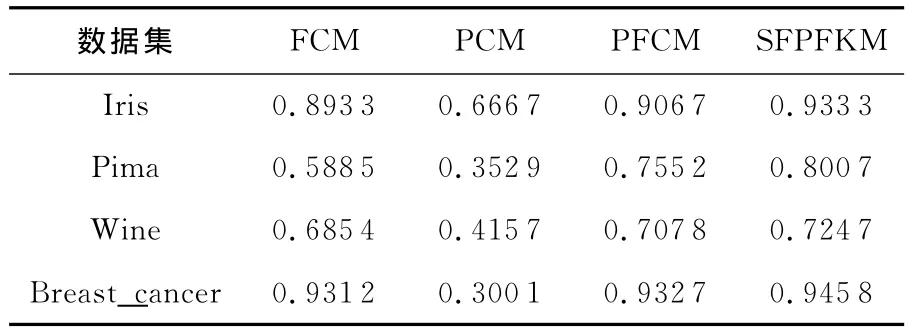
Table 2 Comparision of the algorithms’clustering results表2 各算法的聚类结果比较

从表2中可得，基于样本特征加权可能性模糊聚类算法的聚类精度均优于经典的FCM、PCM、PFCM算法的聚类精度，且对于不同的数据集，本文算法的聚类精度的改善程度是不一样的。与FCM、PCM、PFCM三种算法相比，本文算法在I－ris数据集上的聚类精度比其他三种算法分别提高了近0.14、0.27、0.02；在Pima数据集上的聚类精度分别提高了近0.21、0.44、0.04；在 Wine数据集上的聚类精度分别提高了0.03、0.30、0.01；在Breast＿cancer数据集的聚类精度分别提高了近0.01、0.64、0.01。由此可见，基于样本－特征加权的可能性模糊聚类算法优于经典聚类算法的聚类性能，相比其它算法能获得更好的数据集划分。

4.2 含噪声数据集实验

为了测试本文算法在含噪声数据集上的运行效果，本文对含噪声的数据集X12［19］进 行 实 验 ，X12是由12个数据点构成的二维数据集，其坐标值如表3［19］所示。X12中有10个数据共分为两类，另外两个数据点x6和x12是到两类中心相等的噪声点。实验条件为ε＝0.000 01，最大迭代次数max＿t＝150，m ＝ 2.0，a＝1.0，b＝1.0，β＝2.0，η＝2.0，通过各算法运行后的隶属度值和（或）典型值如表3所示，各算法运行后的聚类中心如表4所示。

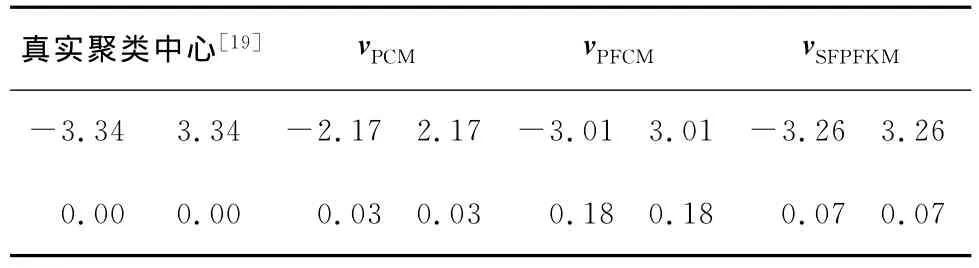
Table 4 Cluster centers of the algorithms表4 各算法的聚类中心

从表3可知，数据点x6和x12在运行FCM算法后的隶属值均为0.5，而实际上x6的隶属值应该要大于x12，因为x6更靠近类的中心，可知FCM算法对噪声比较敏感。PCM算法运行后的典型值分别为0.62和0.08，因为x12比x6更加非典型，其值比x6的典型值要小，故PCM算法减少了噪声数据的影响。PFCM算法运行后的典型值分别为0.49和0.07，而本文算法运行后的典型值分别为0.21和0.02，相比PCM算法，这两种算法的典型值要小些，这就减少了噪声的影响，相比没有典型值的FCM算法，这两种算法都适合处理含噪声的数据，且本文算法更适合处理含噪声的数据集。一般可用算法运行后的聚类中心与真实聚类中心之间的欧氏距离来衡量算法所得聚类中心的偏差。对于PFCM算法和本文算法，可以不断调整a、b的值来计算类中心，选择合适的a、b值可得到最佳的聚类中心。从表4可知，本文算法所得聚类中心离真实类中心最近，其次是PFCM算法，最后是PCM算法，这就说明对含有噪声的数据，本文算法所得的聚类中心比上述算法更接近真实类中心。

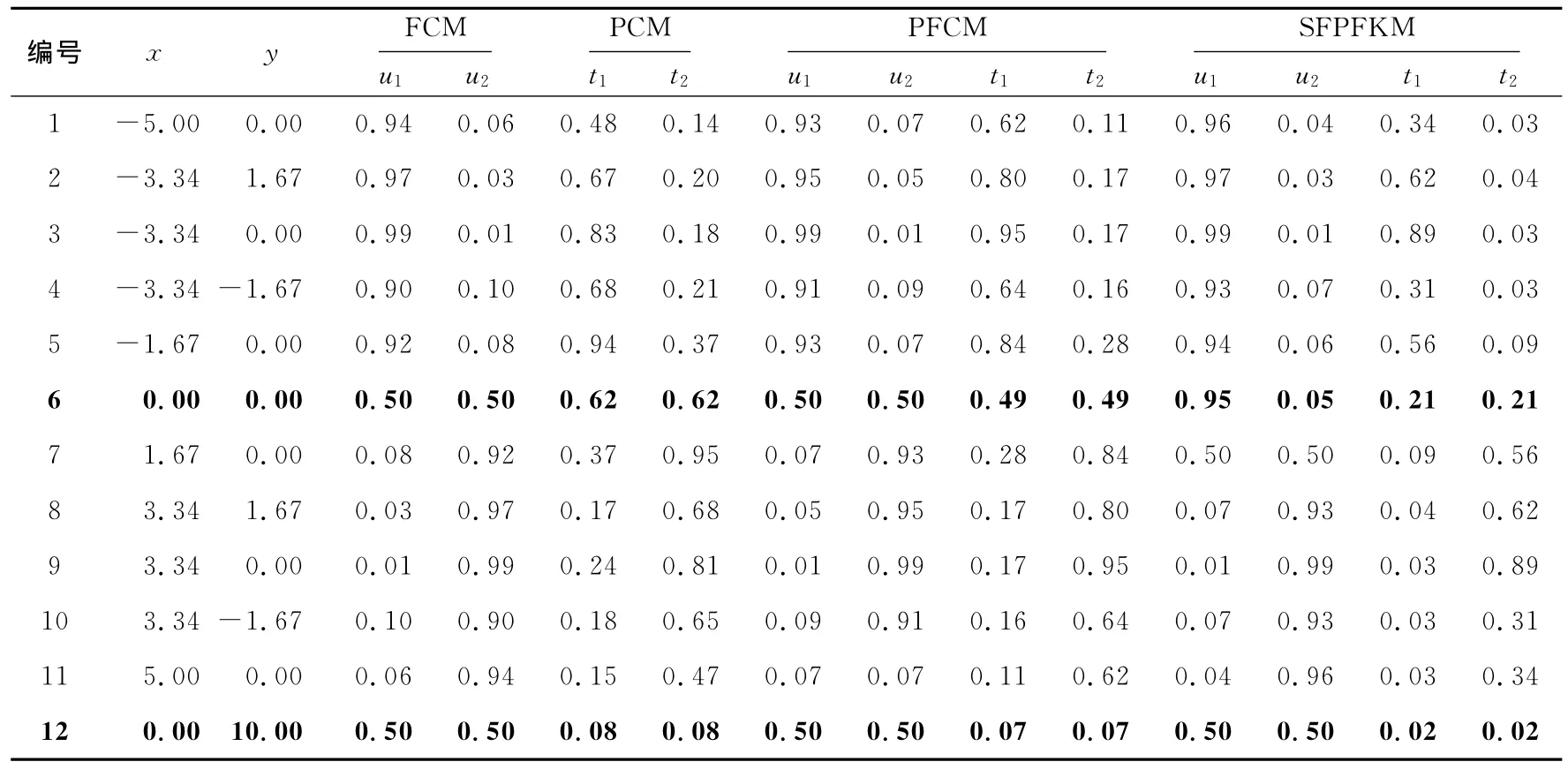
Table 3 Coordinate values of data set X12，memberships and typical values of the algorithms表3 X12数据集的坐标值及各算法运行后的隶属值和（或）典型值

5 结束语

针对经典FCM算法的缺陷，本文提出了基于样本－特征加权的可能性模糊核聚类算法，将可能性聚类应用到模糊聚类中并与FCM算法相结合，在聚类过程中，动态计算各属性特征对聚类类别的权重系数及样本对聚类的重要性权值，并优化选取核参数，不断修正核函数，把原始空间中非线性可分的数据集转化为高维空间中的可分数据集。通过实验将该算法与FCM算法、PCM算法、PFCM算法的聚类性能进行对比，结果表明，基于样本－特征加权的可能性模糊核聚类算法能有效反映属性间的不平衡性，减少噪声数据和例外点的影响，具有更高的聚类精度，比传统的聚类算法具有更好的聚类性能。同时，在聚类算法中如何选取合适的参数值，这需要不断通过实验进行验证。在本文中是将算法运行多次并取不同的参数值，将具有最优聚类效果的参数作为最终的实验参数，因此算法中实验参数的选取、修正核函数的选择以及核参数的优化等，都是本文算法有待继续研究的地方。

［1］ Sun J G，Liu J，Zhao L Y.Clustering algorithms research［J］.Journal of Software，2008，19（1）：48－61.（in Chinese）

［2］ Kirindis S，Chatzis V.A robust fuzzy local information C－means clustering algorithm［J］.IEEE Transactions on Image Process，2010，19（5）：1328－1337.

［3］ Cai W，Chen S，Zhang D.Fast and robust fuzzy C－means clustering algorithms incorporating local information for image segmentation［J］.Pattern Recognition，2007，40（3）：825－838.

［4］ Tian Jun－wei，Huang Yong－xuan，Yu Ya－lin.A fast FCM cluster multi－threshold image segmentation algorithm based on entropy constraint［J］.Pattern Recognition and Artificial Intelligence，2008，21（2）：221－226.（in Chinese）

［5］ Pal N R，Pal K，Keller J，et al.A possibilistic fuzzy C－means clustering algorithm［J］.IEEE Transactions on Fuzzy System，2005，13（4）：517－530.

［6］ Yu Shui－ying，Ding Hua－fu，Fu Zhi－chao.Study on text cat－egorization based on genetic algorithm and fuzzy clustering［J］.Computer Technology and Development，2009，19（4）：131－142.（in Chinese）

［7］ Xu Song－rong.The fuzzy clustering method based on genetic arithmetic［J］.Journal of Huazhong University of Science and Technology（Nature Science Edition），2004，32（10）：217－219.（in Chinese）

［8］ Wang L J，Guan S Y，Wang X L，et al.Fuzzy C mean algorithm based on feature weights［J］.Chinese Journal of Computers，2006，29（10）：1797－1803.（in Chinese）

［9］ Shen Hong－bin，Yang Jie，Wang Shi－tong.Attribute weighted mercer kernel based fuzzy clustering algorithm for general non－shpherical datasets［J］.Soft Computing，2006，10（11）：1061－1073.

［10］ He Yang－cheng，Wang Shi－tong，Jiang Nan.Mercer－kernel based mixed C－means fuzzy clustering algorithm with attributes weights in feature space［J］.Computer Engineering and Applications，2011，47（23）：159－163.（in Chinese）

［11］ Cai Jing－ying，Xie Fu－ding，Zhang Yong.New fuzzy clustering algorithm based on feature weighted Mahalanobis distances［J］.Computer Engineering and Applications，2012，48（5）：198－200.（in Chinese）

［12］ Liu Bing，Xia Shi－xiong，Zhou Yong，et al.A sample－weighted possibilistic fuzzy clustering algorithm［J］.Acta Electronica Sinica，2012，2（2）：371－375.（in Chinese）

［13］ Yang M S，Wu K L.Unsupervised possibilistic clustering［J］.Pattern Recognition，2006，39（1）：5－21.

［14］ Pan Qing－feng，Chen Shui－li，Chen Guo－long.Study on fuzzy C－means clustering algorithm based on kernel function［J］.Journal of Jimei University：Natural Science，2006，11（4）：369－373.（in Chinese）

［15］ Zhang Xiang，Xiao Xiao－ling，Xu Guang－you.A new method for determining the parameter of Gaussian kernel［J］.Computer Engineering，2007，6（12）：52－56.（in Chinese）

［16］ Amari S，Wu S.Improving support vector machine classifiers by modifying kernel functions［J］.Neural Networks，1999，12（6）：783－789.

［17］ Li Hong－ying，Zhong Bo.Modifying kernel function for support vector machines classifier［J］.Computer Engineering and Applications，2009，45（24）：53－55.（in Chinese）

［18］ Tushir M，Srivastava S.A new kernelized hybrid C－mean clustering model with optimized parameters［J］.Applied Soft Computing，2010，10（2）：381－389.

［19］ Pal N R，Pal K，Bezdek J C.A new hybrid C－means clustering model［C］∥Proc of the IEEE International Conference on Fuzzy Systems，2004：179－184.

附中文参考文献：

［1］ 孙吉贵，刘杰，赵连宇.聚类算法研究［J］.软件学报，2008，19（1）：48－61.

［4］ 田军委，黄永宣，于亚琳.基于熵约束的快速FCM聚类多阈值图像分割算法［J］.模式识别与人工智能，2008，21（2）：221－226.

［6］ 于水英，丁华福，付志超.基于遗传算法和模糊聚类的文本分类研究［J］.计算机技术与发展，2009，19（4）：131－142.

［7］ 许松荣.基于遗传算法的模糊聚类算法［J］.华中科技大学学报（自然科学版），2004，32（10）：217－219.

［8］ 王丽娟，关守义，王小龙，等.基于属性权重的 Fuzzy CMeans算法［J］.计算机学报，2006，29（10）：1797－1803.

［10］ 贺杨成，王士同，江南.特征空间属性加权混合C均值模糊核聚类算法［J］.计算机工程与应用，2011，47（23）：159－163.

［11］ 蔡静颖，谢福鼎，张永.基于马氏距离特征加权的模糊聚类新算法［J］.计算机工程与应用，2012，48（5）：198－200.

［12］ 刘兵，夏士雄，周勇，等.基于样本加权的可能性模糊聚类算法［J］.电子学报，2012，2（2）：371－375.

［14］ 潘庆丰，陈水利，陈国龙.基于核函数的模糊C均值聚类算法［J］.集美大学学报，2006，11（4）：369－373.

［15］ 张翔，肖小玲，徐光佑.一种确定高斯核函数模型参数的新方法［J］.计算机工程，2007，6（12）：52－56.

［17］ 李红英，钟波.支持向量分类机的修正核函数［J］.计算机工程与应用，2009，45（24）：53－55.