基于匹配延拓的ITD边界效应抑制方法研究

胥永刚, 陆 明, 付 胜, 张建宇

(北京工业大学 机电学院 北京市先进制造技术重点实验室，北京 100124)

大型机电设备的轴承齿轮等零部件发生故障时，振动信号常呈现出非线性非平稳特征，且淹没于强烈的背景噪声中。如何处理复杂的非平稳振动信号，一直是故障诊断领域的研究热点之一[1]。

Frei等[2]提出了一种新的非线性非平稳信号处理方法——固有时间尺度分解法(Intrinsic time-scale decomposition, ITD),并将该方法应用于生物医学信号处理中, 取得了理想的效果。ITD 分解法可以自适应地将任意复杂信号分解为若干具有实际物理意义的固有旋转分量(Proper Rotation Component, PRC) 和一个单调趋势项，然后再进一步求出所有PRC 的瞬时幅值和瞬时频率，即可得到原始信号完整的时频分布。该方法一经提出，便迅速在通信[3]、空间信息[4]及故障诊断[5-7]领域得到应用，均取得了不错的效果。

在ITD方法的应用过程中，分解所得的固有旋转分量常在边界处出现畸变，使得分解结果严重失真，称之为ITD方法的边界效应。本文对比分析了五种数据延拓方法(自适应波形匹配法、基于AR模型的延拓方法、镜像延拓方法、多项式延拓方法和反对称周期延拓法)在ITD边界效应抑制中的应用，并以趋势分量绝对值累加和为评价指标，判定基于自适应波形匹配方法的数据延拓更适合抑制ITD边界效应，分解误差最小。最后，将其运用到实际信号的分析，验证了该方法的有效性。

1 ITD方法及其边界效应

1.1 ITD方法的基本原理

设待分解信号Xt为一实值离散信号，{τk,k=1,2,…}代表Xt中所有局部极值点对应的时刻，方便起见，定义τ0=0。定义L为Xt的基线提取算子，一次ITD分解是将信号Xt分解为基线分量Lt和固有旋转分量Ht，即[2]：

Xt=LXt+(1-L)Xt=Lt+Ht

(1)

式中，Lt=LXt为基线分量，代表信号中的局部相对低频成分；Ht=(1-L)Xt为固有旋转分量，表示信号中的局部相对高频成分。

简便起见，令Xk和Lk分别表示X(tk)和L(tk)，设Lt)和Ht在[0,τk]上有定义，Xt在[0,τk+2]上有定义，则在连续极值点间隔[τk,τk+1]上可定义该区间内Xt的分段线性基线提取因子L：

(2)

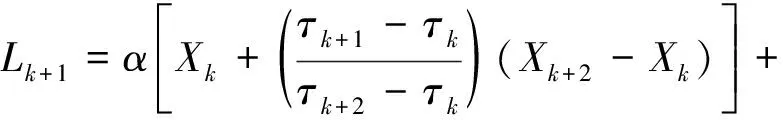
(3)

式中，α用于控制提取固有转动分量幅度的线性缩放，α∈[0,1]，通常取α=0.5[2]。则，固有旋转因子Ht为：

HXt=(1-L)Xt=Ht=Xt-Lt

(4)

这种基线构造方法形成的基线分量Lt保留了信号在各个极值点之间的单调性，提取了各个极值点之间叠加的局部高频分量，即固有于信号某种尺度上的分量——固有旋转分量。将基线分量当做新的待分解信号重复以上的分解过程，可以得到一系列的固有旋转分量，直到获得一个单调趋势信号。这就将原始信号Xt分解成若干个从高到低不同频率段的固有旋转分量之和与一个单调趋势分量。整个过程可表示为：

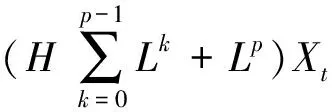
(5)

式中，HLkXt是第(k+1)层固有旋转分量，LpXt是单调的趋势或提取的最低频率基线。

1.2 ITD方法的边界效应

设有一仿真信号：

x(t)=(1+0.5cos(2π×5t))cos(2π×100t+1.5sin(2π×7t))+0.5sin(2π×30t)

(6)

该信号包括两个主要分量：一是调幅-调频分量，二是纯正弦分量。该信号的时域波形如图1所示。

图1 仿真信号的时域波形

该信号的ITD分解结果如图2所示。由图可知，原始信号x(t)被分解为2个固有旋转分量(记为PRC1～PRC2)和一个趋势分量(记为L)，其中PRC1和PRC2能量较大，分别对应原始信号中的调幅-调频分量和正弦分量，L能量很小，为ITD分解过程中最终剩余的趋势分量。可见，ITD方法能够将复杂的非平稳信号分解为若干个简单的固有旋转分量和一个趋势分量。

仔细观察所有的PRC分量，还可发现ITD分解过程中几乎所有的PRC分量在边界处均出现了不同程度的畸变，与理论的分量信号存在差别，同时趋势分量L理论上应为常数0，但实际所得L分量在波形中部出现细微波动，两端出现较大的抖动，与理论分析严重不符，此即ITD分解过程中的边界效应，应设法予以抑制或消除。

图2 仿真信号的ITD分解结果

2 基于数据延拓的ITD边界效应的抑制方法

2.1 自适应波形匹配延拓法

抑制边界效应最有效的方法是对端点处的数据进行延拓，延拓的波形须符合原始数据在端点处的变化趋势，否则易产生附加的极值点。在机械设备故障诊断中，原始振动信号在端点处的变化趋势通常在信号的内部也会存在，故可用信号内部某一段与信号端点处变化趋势相同的子波对端点以外的信号进行延拓，从而最大限度维持信号在端点处的变化规律。

(7)

自适应波形匹配方法的具体步骤如下[8]：

(1) 设x(t)为原始信号，确定x(t)最左端的两个相邻极值点，不妨设其分别为极大值点和极小值点，分别记为P0和P1，从起始点到P1的这段波形记为w0，设其长度为l；

(2) 设Emax为x(t)的极大值点集合，以Emax-{P0}中的每一个极大值点Pi作为参考点，计算该段相同长度的波形wi和w0的匹配度M(w0,w1,Pi)；记

M(w0,wi0,Pi0)=min{M(w0,wi,Pi),i=1,2,…}

(8)

(3) 若M(w0,wi0,Pi0)<α·l,其中α为一常数，则取wi0左侧包含了一个极大值和极小值的子波, 作为原始x(t)左端的延拓, 延拓完毕，否则转(4)；

(4) 直接指定端点处的极大和极小值：取原始信号最左端的两个相邻极大值点的均值作为左端点的极大值，取信号最左端的两个相邻极小值点的均值作为左端点的极小值，延拓完毕。

仍采用1.2节中的仿真信号，首先对该信号进行自适应波形匹配延拓，然后再进行ITD分解，最后对分解结果进行截断以保留与原始信号相对应的部分，结果如图3所示。

图2中，趋势分量的幅值约在-0.6～0之间，而图3中趋势分量的幅值约在-0.025～0.025之间，分解误差显著减小，故对原始信号进行自适应波形匹配延拓后再做ITD分解，可以有效地抑制ITD分解过程中的边界效应，减少因为边界效应产生的误差。

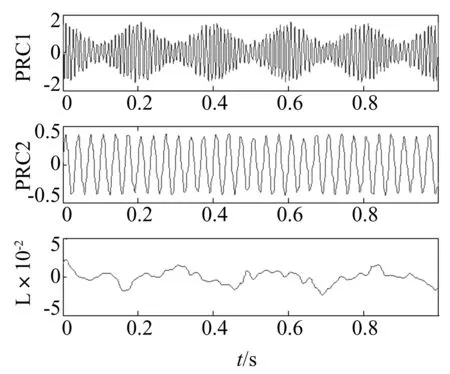
图3 仿真信号的ITD分解结果

2.2 镜像延拓法

镜像延拓相当于放一面镜子在信号的端点，这样在镜子里就会出现一个与原始信号相反的信号。若原始信号为x(n)，其中n∈(1,2,3,…,N)，则镜中的信号xj(m)为，

xj(m)=x(N+1-m)m∈(1,2,3,…,N)

(9)

将xj(m)与x(n)尾首相连，就得到了镜像延拓后的信号。

仍采用前述仿真信号，用ITD分解经镜像延拓后的信号，再截取与原始信号相对应的部分，得到结果如图4所示。使用镜像延拓法，ITD分解的边界效应在一定程度上得到抑制，趋势分量畸变的波动范围较图2有所改善，但其波动幅值远大于图3，边界效应抑制不太理想。

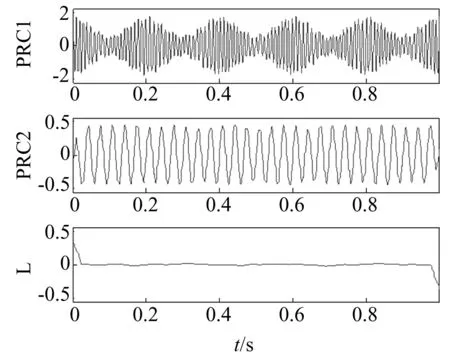
图4 仿真信号的ITD分解结果

2.3 多项式拟合延拓法

多项式拟合法是通过信号极大值或者极小值本身特征拟合多项式，来确定延拓的极值点[9]，具体方法如下：

(1) 在数据的极大值或者极小值的集合中，提取靠近两端的几个极值点。

(2) 用提取出来的极大值或是极小值拟合多项式。

(3) 选取在数据两端之外的两个时刻，用多项式计算出这两个时刻所对应的函数值。将该函数值作为延拓的极值点，对应的时刻作为出现的时间。

同样采用上述的仿真信号，得到的结果如图5所示。ITD分解的边界效应得到了有效的抑制，并且分解得到的误差项非常小，说明这种方法对于模拟信号是有效的。

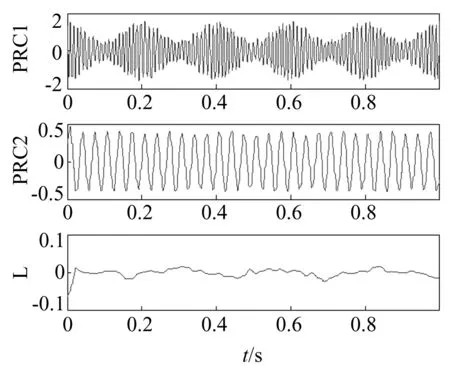
图5 仿真信号的ITD分解结果

2.4 基于AR模型预测延拓法

AR模型可以根据数据点之间的相关性，预测数据的未来值[10]。对于一个时间序列x，若其第n个点x(n)的取值与其前m个点(x(n-1)…x(n-m))都有关，就可以用这m个点建立AR模型，来预测x(n)。其AR模型为

(10)

基于AR模型信号的边界延拓的具体步骤为：

(1) 选取数据点建立AR模型。

(2) 根据模型预测数据，进行延拓。

采用前述同样的仿真信号，首先对其进行AR模型延拓，然后再进行ITD分解，得到的结果如图6所示。信号分解后的分解误差较小，而且PRC分量只有略微的畸变，说明该方法抑制模拟信号边界问题的效果较好。

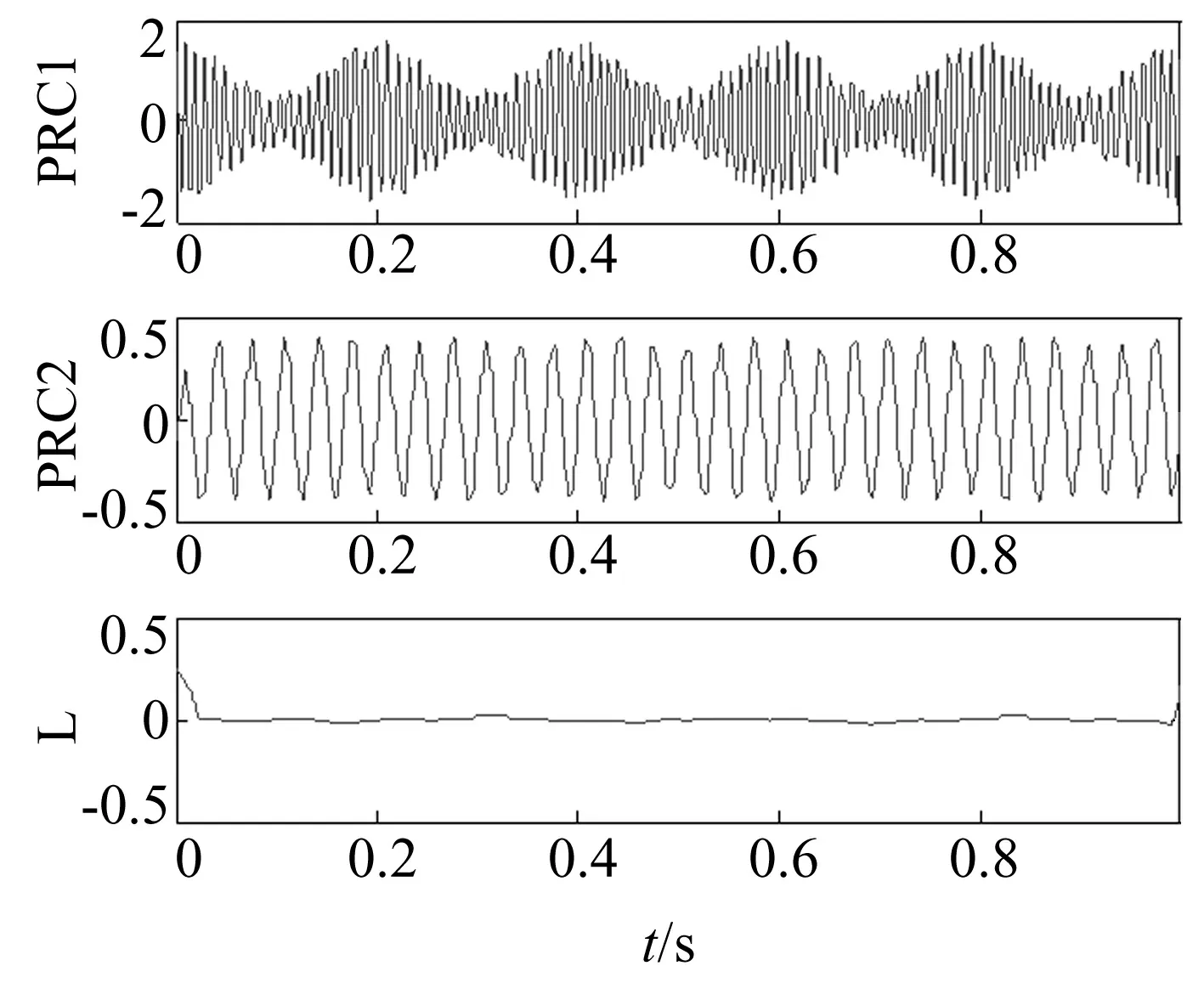
图6 仿真信号的ITD分解结果

2.5 反对称周期延拓法

如果信号x(n)满足下列情况，可以用反对称周期延拓法[11]。

x(1)=0
x(2)-x(1)≠0

(11)

反对称周期延拓法的具体步骤如下：

(1) 对于原始信号取负处理，即

y(n)=-x(n)

(12)

(2) 将得到的信号y(n)以n/2为中心对调，使信号y(n)的首尾对调，得到新的信号z(n)。

(3) 将z(n)与x(n)首尾相连得到延拓后的信号。

对前述仿真信号进行反对称周期延拓之后再进行ITD分解，也得到了两个PRC分量和一个趋势分量，结果如图7所示。虽然第二个PRC分量中还含有一定的边界效应，该方法仍对于原始的边界效应有抑制效果，使得ITD得到的分解误差也较小。

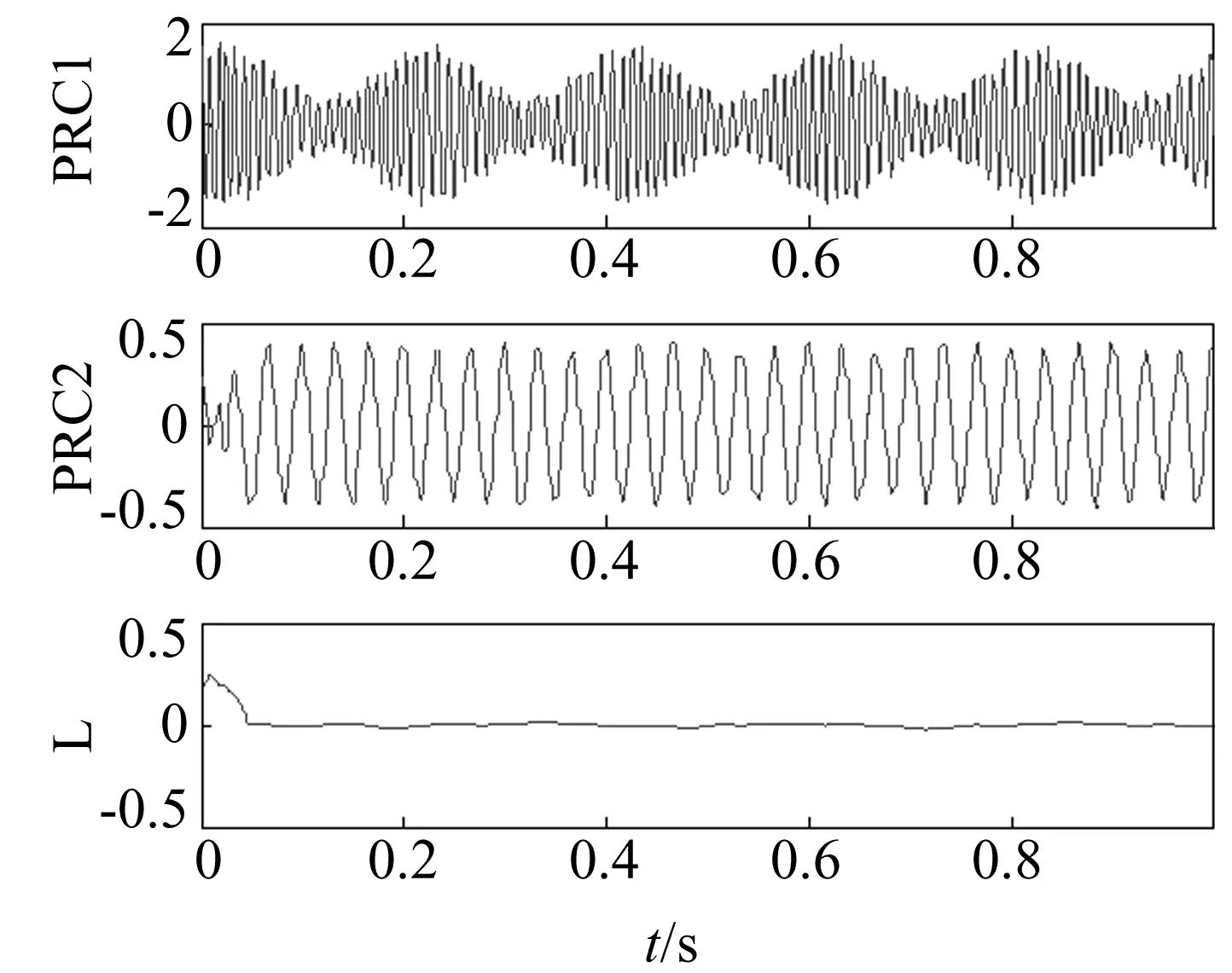
图7 仿真信号的ITD分解结果

2.6 延拓方法的数学模拟比较

同一个仿真信号，经过上述五种波形延拓方法之后再进行ITD分解，得到了五组不同的ITD分解结果。这五组结果都是由两个PRC分量和一个趋势分量组成。造成趋势分量畸变的主要原因在于边界效应，在该仿真信号中，趋势分量的理论值应为常数0，故可用分解所得趋势分量与理论值(常数0)之间的差异来定量表征不同延拓方法对ITD分解边界效应的抑制效果。设系数ξ为

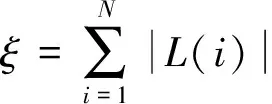
(13)

其中：L为ITD分解的趋势分量，N为趋势分量的数据长度。ξ用来定量表征趋势分量L与理论值之间的差距。ξ值越大，说明趋势分量L较大，边界效应抑制效果差。ξ值越小，说明趋势分量L较小，边界效应抑制效果好。前述5种不同数据延拓方法中的ξ值如表1所示。

通过比较可以看出，ξ值最小为13.2，其对应方法为自适应波形匹配法，所以抑制ITD分解边界效应最好的数据延拓方法为自适应波形匹配法。

表1 不同方法ξ值统计

3 工程应用

实验系统由轴承实验台、压电式加速度传感器、数据采集仪、笔记本电脑组成，如图8所示。将带有人工模拟故障的轴承安装在实验台上，进行实验数据的采集和分析。

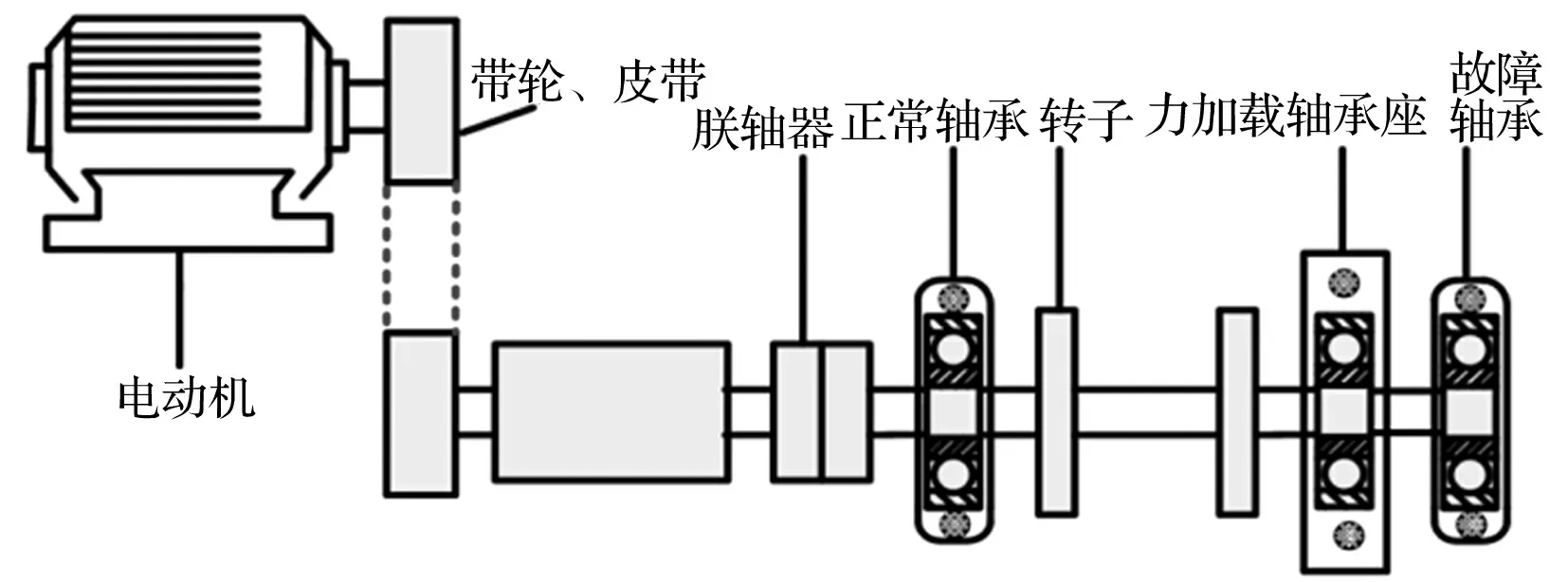
图8 轴承故障模拟实验台

该实验的滚动轴承型号为NU205EM，上有人工模拟的内圈点蚀故障，电机转速为310 r/min，皮带轮传动比为1∶1。振动加速度信号的采样频率为5 000 Hz，采样点数为8 192，经过计算故障的特征频率为39.7 Hz。图9(a)和(b)分别为滚动轴承内圈点蚀故障的时域波形及其幅值谱。

图9 原始信号的时域波形及其幅值谱

由图9可以看出，时域波形中出现等间隔的冲击成分，幅值谱中亦含有明显的边频带，说明原始信号中存在着典型的调制现象。利用自适应波形匹配延拓法对该数据进行延拓，然后再进行ITD分解并截取，得到8个PRC分量和一个趋势分量，其中前三个PRC分量包含有明显的调制信息，如图10所示。

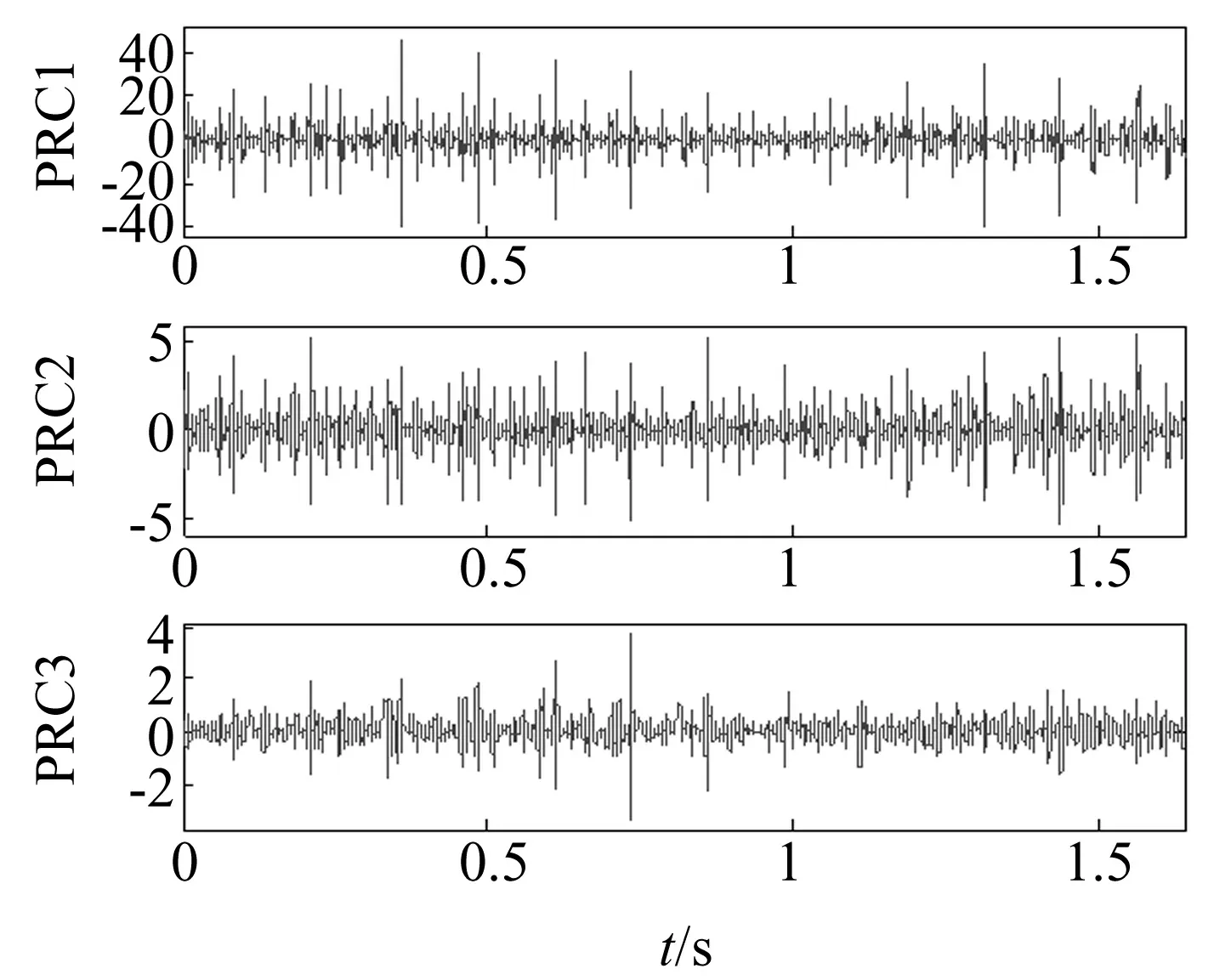
图10 前三个PRC分量的时域波形

对这三个PRC分量进行Hilbert包络解调，得到其包络谱，如图11所示。在三个包络谱中能明显地看到轴承内圈的故障特征频率39.7Hz，在前两个PRC分量的包络谱中还能清晰地看到39.7 Hz的倍频成分，因此，可以肯定地判断该轴承存在内圈故障，与预设的故障类型完全吻合。

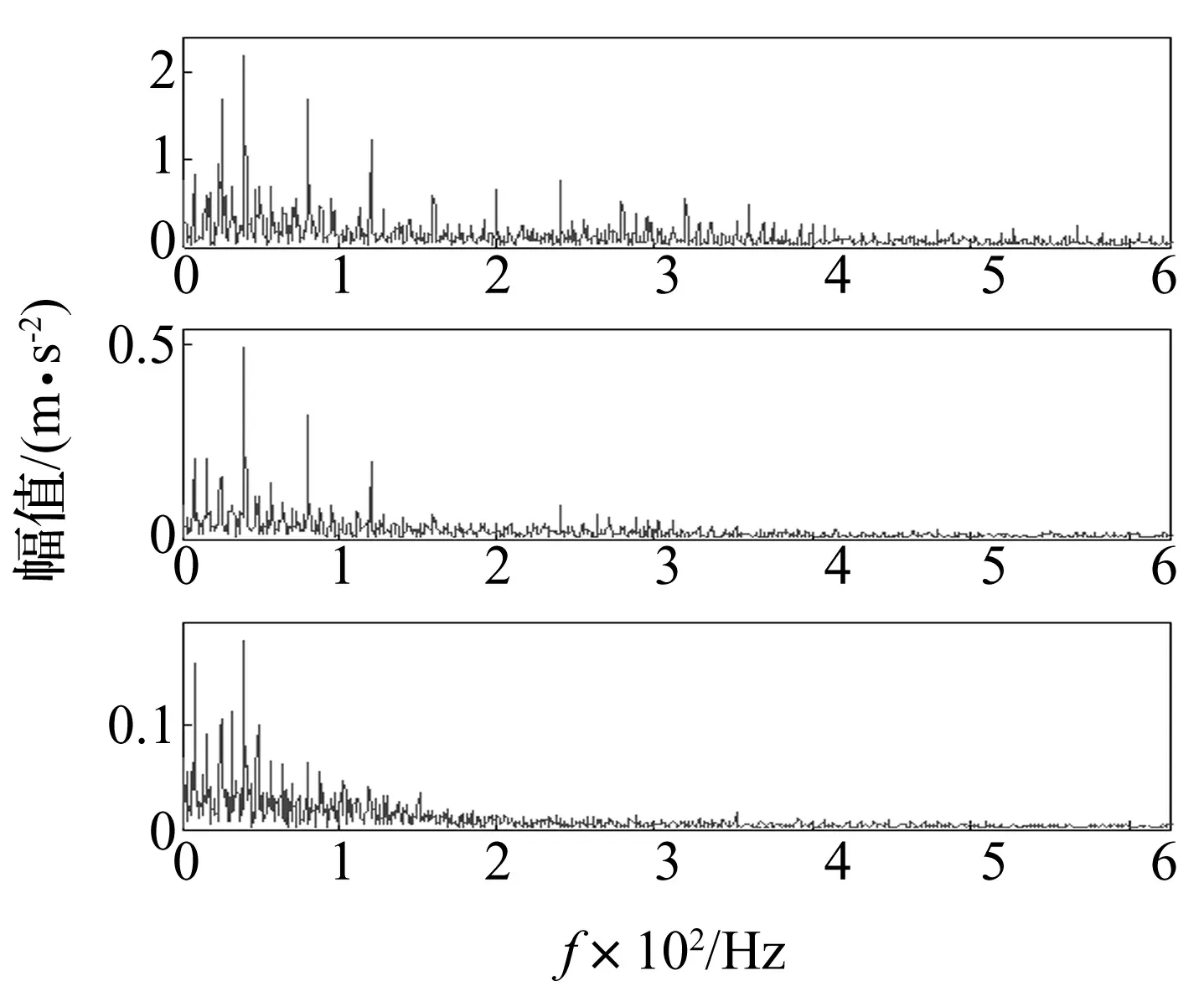
图11 前三个PRC分量的包络谱

4 结 论

(1) ITD法可将一个复杂的非平稳信号分解为若干个固有旋转分量和一个趋势分量，便于融合其它现代信号处理方法进行故障特征的深层次挖掘。

(2) 自适应波形匹配法、基于AR模型的延拓方法、镜像延拓方法、多项式延拓方法、反对称周期延拓法，均可有效地抑制边界效应，使分解所得的PRC分量端点处畸变小。通过仿真实验比较，自适应波形匹配的抑制效果最佳。

(3) 将自适应波形匹配应用于滚动轴承内圈点蚀故障振动信号特征提取，实验表明该方法能精确提取信号典型故障特征，在故障诊断领域具有很好的应用前景。

参 考 文 献

[1]Yang Y, Peng Z K, Meng G. Characterize highly oscillating frequency modulation using generalized warblet transform[J]. Mechanical Systems and Signal Processing, 2012, 26: 128-140.

[2]Frei M G, Osorio I. Intrinsic time-scale decomposition：time-frequency-energy analysis and real-time filtering of non-stationary signals[J]．Proceedings of the Royal Society A, 2007, 463: 321-342.

[3]安金坤, 田 斌, 孙永军,等. 一种基于ITD算法的直扩信号检测算法[J]. 电子与信息学报，2010,32(5): 1178-1182.

AN Jin-kun, TIAN Bin, SUN Yong-jun, et al. An alagorithm for direct sequence spread spectrum signal detection based on intrinsic time-scale decomposition[J]. Journal of Electronics & information Technology, 2010, 32(5): 1178 -1182.

[4]顾小昕. 基于固有时间尺度分解的信号分析与干扰抑制技术研究[D]. 西安：西安电子科技大学, 2010.

[5]AN Xue-li, JIANG Dong-xiang, CHEN Jie, et al. Application of the intrinsic time-scale decomposition method to fault diagnosis of wind turbine bearing[J]. Journal of Vibration and Control, 2012,18(2): 240-245.

[6]LIN Jin-shan. Improved intrinsic time-scale decomposition method and its simulation[J].Frontiers of Manufacturing and Design Science II, 2011,121: 2045-2048.

[7]HAN Jing-tao, JIAO Si-hai, JIANG Zheng-yi. The de-noising algorithm based on intrinsic time-scale decomposition[J]. Advanced Materials Research, 2011,422: 347-352.

[8]邵晨曦, 王剑, 范金锋,等. 一种自适应的EMD端点延拓方法[J]. 电子学报, 2007，35(10): 1944-1948.

SHAO Chen-xi, WANG Jian, FAN Jin-feng, et al. A self-adaptive method Dealing with the end Issue of EMD[J]. Acta Electronica Sinica, 2007，35(10): 1944-1948.

[9]许宝杰, 张建民, 徐小力,等.抑制EMD端点效应方法的研究[J]. 北京理工大学学报,2006,26(3): 196-200.

XU Bao-jie, ZHANG Jian-min, XU Xiao-li, et al. A study on the method of restraining the ending effect of empirical mode decomposition[J]. Transactions of Beijing Institute of Technology,2006,26(3): 196-200.

[10]胡劲松, 杨世锡. EMD方法基于AR模型预测的数据延拓与应用[J]. 振动、测试与诊断,2007,27(2): 116-120.

HU Jin-song, YANG Shi-xi. AR model prediction-based EMD method and its application to data extension[J]. Journal of Vibration, Measurement & Diagnosis, 2007, 27(2): 116-120.

[11]赵娜. HHT经验模式分解的周期延拓方法[J]. 计算机仿真,2008,25(12): 346-350.

ZHAO Na. A periodic extension approach for HHT empirical mode decomposition[J]. Computer Simulation, 2008, 25(12): 346-350.