时滞对典型二阶振荡系统稳定性的影响

张 勇， 王 宁

(中国石油大学 信息与控制工程学院，青岛 266580)

凡以二阶微分方程作为运动方程的控制系统，称为二阶系统。在控制工程中，不仅二阶系统的典型应用极为普遍，而且不少高阶系统的特性在一定条件下可用二阶系统的特性来表征。因此，着重研究二阶系统的分析和计算方法，具有较大的实际意义[1-3]。

控制系统的闭环稳定性是系统分析和设计所需解决的首要问题，Nyquist稳定判据是一种常用的频域稳定判据，其特点是根据开环系统的频率特性曲线判定闭环系统的稳定性。由于其在使用上非常方便和直观，在系统稳定性研究中得到了广泛的应用[4-6]。

目前，国际上对时滞与稳定性相关问题的研究， 一般只考虑时滞对系统性能的负面影响，认为时滞越小，系统性能越好。给出的研究结果只能保证时滞本身在小于某个上界时才能满足系统的某些性能指标。这种研究思想只适合时滞相对较小的情形，结果仍是比较保守的[7-9]。Abdallah等[10]提出时滞的正反馈控制可以稳定化具有振荡特性的系统。此研究结果表明，在一定条件下，时滞对系统性能具有正面影响。随后，胡海岩等[11]运用Routh-Hurwitz稳定判据和广义Sturm判别法，讨论了含待定参数的高阶时滞动力系统的稳定性切换问题，在时滞动力系统的稳定性与分岔方面做了大量的研究工作。在此基础上，唐功友[12]运用Nyquist稳定判据和坐标变换方法，研究了弹簧-质量-阻尼器机械位移系统的最大稳定裕度时滞比例控制器的设计问题，实现了主动利用时滞反馈控制镇定振荡系统的目的。

关于时滞对典型二阶振荡系统的稳定性是否具有正面作用这一议题，本文进行了全面细致的稳定性分析，分别讨论了闭环系统为单位负反馈和单位正反馈两种情形下时滞对控制系统性能的影响。通过绘制相对阻尼系数在不同取值区间的Nyquist曲线，得出了时滞与闭环系统稳定性的关系，并针对各种情况进行了单位阶跃响应的实例仿真。

1 二阶振荡系统描述

考虑如下一类含有时滞的闭环控制系统

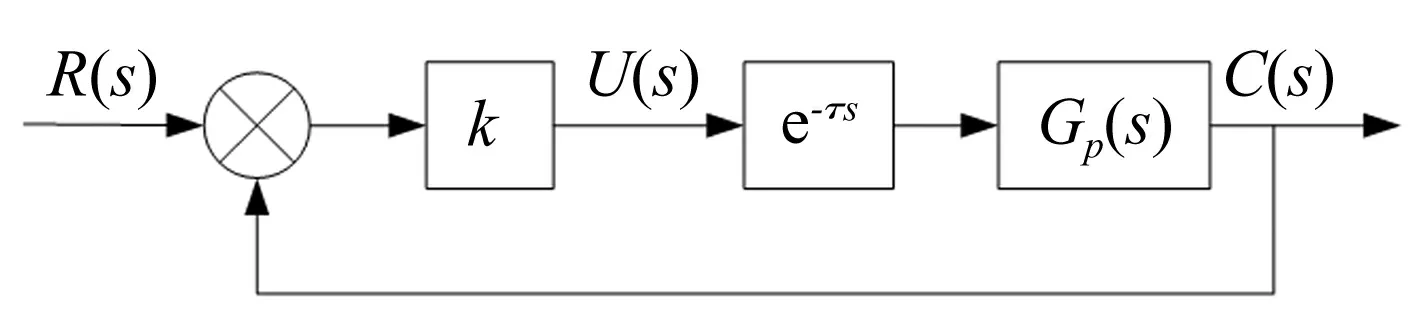
图1 闭环控制系统结构

其中：R(s)表示参考信号，C(s)表示输出信号，U(s)表示控制信号，k>0为比例控制器增益，τ≥0为信号传输时滞对控制系统的综合效应，Gp(s)为具有二阶系统标准形式的被控对象。

(1)

其中：ωn>0表示无阻尼振荡频率，ζ表示相对阻尼系数。

系统的开环传递函数可以表示为

(2)

其频率特性为

(3)

2 负反馈稳定性分析

当闭环控制系统采用单位负反馈时，系统的闭环传递函数可以表示为

(4)

当τ=0时，闭环系统的特征方程为

(5)

其特征根为

(6)

由代数稳定判据可以得到此时闭环系统稳定的充要条件是ζ>0。

以下我们分析当τ>0时闭环系统的稳定性。

1) 当ζ=0时，开环传递函数在右半s平面无极点，由Nyquist稳定判据可知闭环系统稳定的充要条件

是Nyquist曲线不包围或穿越临界点(-1,j0)。

系统的开环传递函数可以表示为

(7)

其频率特性为

(8)

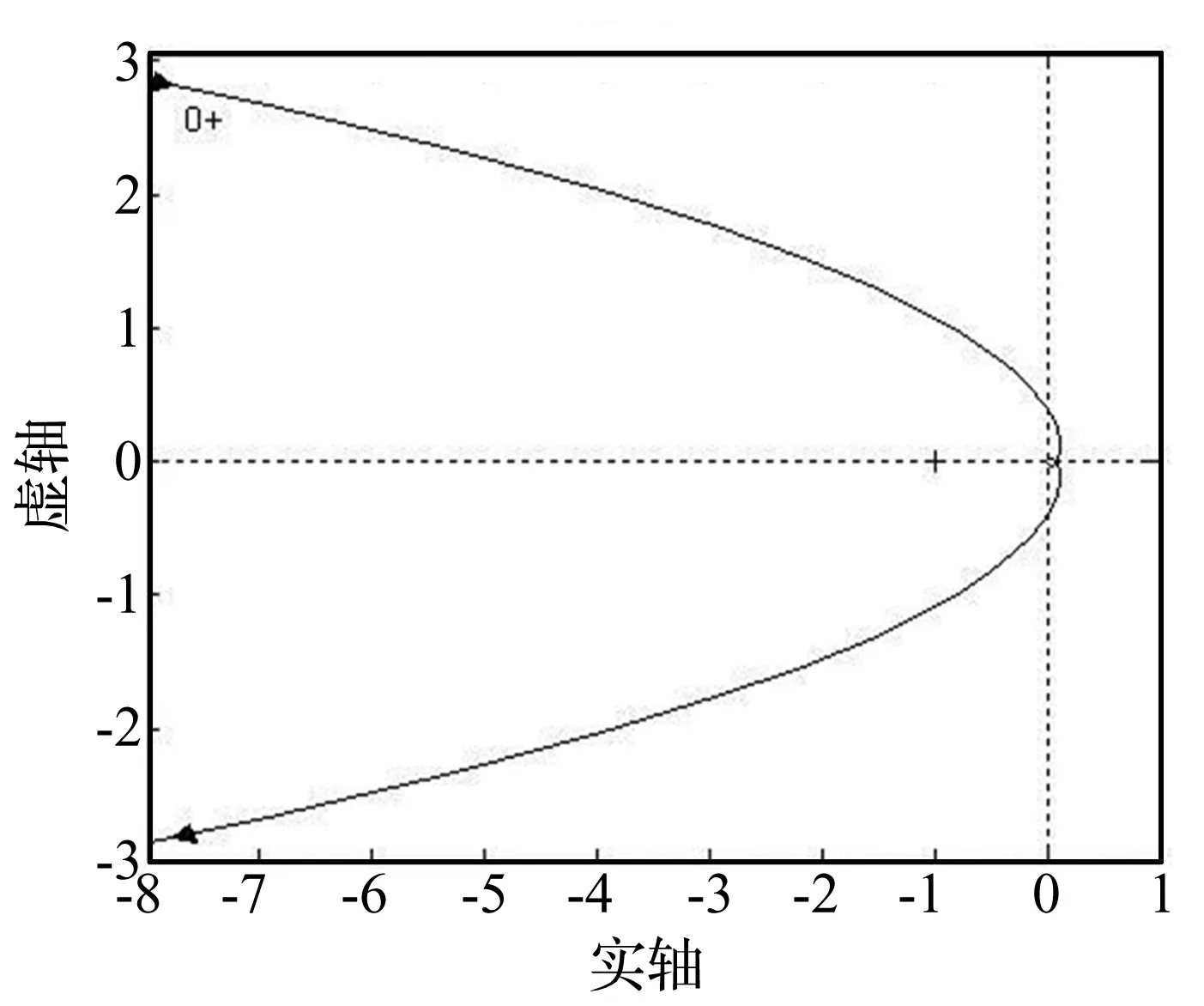
图2 负反馈ζ=0时系统的Nyquist曲线

由于开环传递函数包含两个积分环节，为了便于分析我们可以从与频率0+对应的点开始逆时针方向补画1/2个半径无穷大的圆。又由于Nyquist曲线相对实轴有对称性，可见在ω∈(-∞,+∞)范围内Nyquist曲线绕临界点(-1,j0)顺时针转过一圈，所以此时无论我们如何选取k和τ的值，系统都不稳定。

取ωn=1,k=1,τ=1时，闭环系统的单位阶跃响应曲线如图3所示。

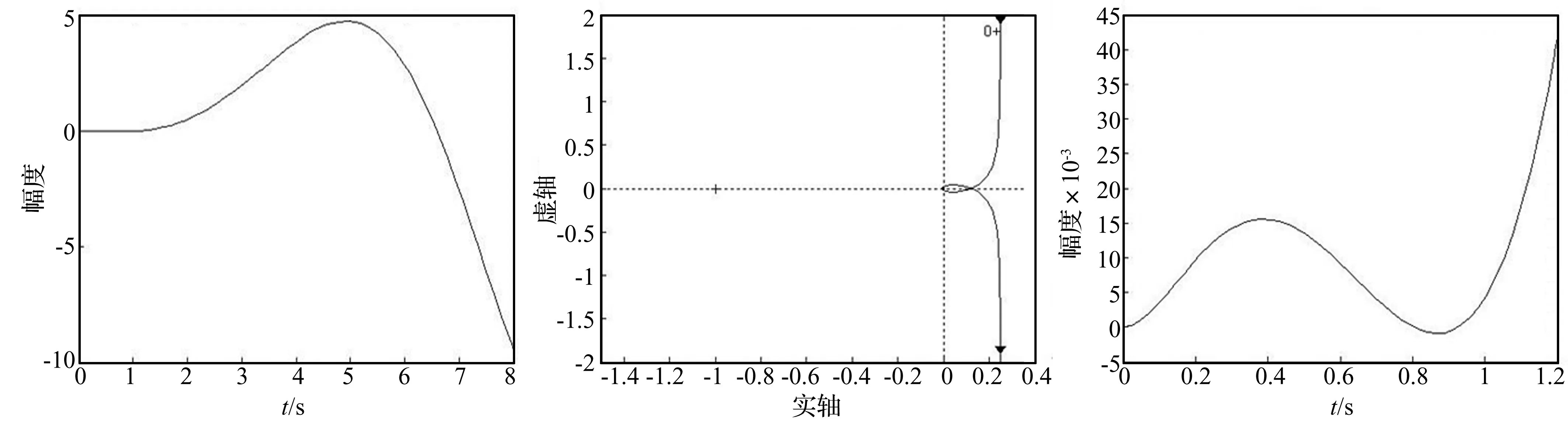
图3 负反馈ζ=0时系统的单位阶跃响应

2) 当ζ<0时，开环传递函数在右半s平面有一个极点，由Nyquist稳定判据可知闭环系统稳定的充要条件是Nyquist曲线逆时针包围临界点(-1,j0)一圈。

系统开环传递函数的幅频特性为

(9)

系统开环传递函数的相频特性为

(10)

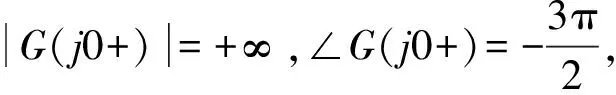
由于开环传递函数包含一个积分环节，我们可以从与频率0+对应的点开始逆时针方向补画1/4个半径无穷大的圆。又由于Nyquist曲线相对实轴有对称性，可见在ω∈(-∞,+∞)范围内Nyquist曲线绕临界点(-1,j0)顺时针转过两圈，所以此时无论我们如何选取ζ，k和τ的值，系统都不稳定。

取ωn=1,k=1,τ=1,ζ=-1时，闭环系统的单位阶跃响应曲线如图5所示。

3) 当ζ>0时，开环传递函数在右半s平面无极点，由Nyquist稳定判据可知闭环系统稳定的充要条件是Nyquist曲线不包围或穿越临界点(-1,j0)。

(11)

(12)

此时系统的Nyquist曲线如图6所示。

由于开环传递函数包含一个积分环节，我们可以从与频率0+对应的点开始逆时针方向补画1/4个半径无穷大的圆。又由于Nyquist曲线相对实轴有对称性，可见当Nyquist曲线与实轴的交点小于等于-1时，系统不稳定，当Nyquist曲线与实轴的交点大于-1时，系统稳定。

当系统不稳定时，由:

(13)

可以求得Nyquist曲线与以坐标原点为圆心的单位圆的交点频率为

(14)

由式(10)我们可以得到，此时如下不等式成立

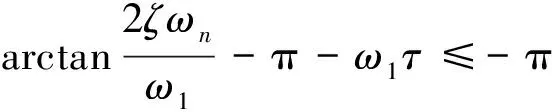
(15)

基于此我们可以求出系统不稳定时τ的取值范围为

(16)

上式左右两边的不等式是等价的。

取ωn=1,k=1,τ=1,ζ=1时，闭环系统的单位阶跃响应曲线如图7所示。

取ωn=1,k=1,τ=4,ζ=1时，闭环系统的单位阶跃响应曲线如图8所示。

图6 负反馈ζ>0时系统的Nyquist曲线

3 正反馈稳定性分析

当闭环控制系统采用单位正反馈时，我们通过研究下式的Nyquist曲线对闭环系统进行稳定性分析。

(17)

其频率特性为

(18)

系统的闭环传递函数可以表示为

(19)

当τ=0时，闭环系统的特征方程为

(20)

其特征根为

(21)

由代数稳定判据可以得到，此时无论我们如何选取ζ的值，系统都不稳定。

以下我们分析当τ>0时闭环系统的稳定性。

1) 当ζ=0时，开环传递函数在右半s平面无极点，由Nyquist稳定判据可知闭环系统稳定的充要条件是Nyquist曲线不包围或穿越临界点(-1,j0)。

Nyquist曲线的绘制函数可以表示为:

(22)

其频率特性为

(23)

由于开环传递函数包含两个积分环节，我们可以从与频率0+对应的点开始逆时针方向补画1/2个半径无穷大的圆。又由于Nyquist曲线相对实轴有对称性，可见在ω∈(-∞,+∞)范围内Nyquist曲线绕临界点(-1,j0)顺时针转过一圈，所以此时无论我们如何选取k和τ的值，系统都不稳定。

取ωn=1,k=1,τ=1时，闭环系统的单位阶跃响应曲线如图10所示。

2) 当ζ>0时，开环传递函数在右半s平面无极点，由Nyquist稳定判据可知闭环系统稳定的充要条件是Nyquist曲线不包围或穿越临界点(-1,j0)。

Nyquist曲线绘制函数的幅频特性为:

(24)

Nyquist曲线绘制函数的相频特性为:

(25)

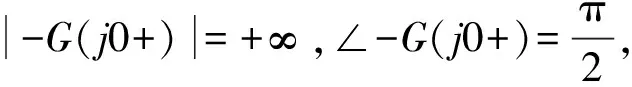
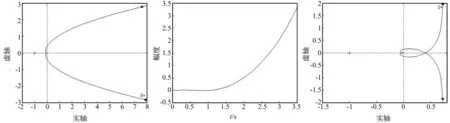
图9 正反馈ζ=0时系统的Nyquist曲线

由于开环传递函数包含一个积分环节，我们可以从与频率0+对应的点开始逆时针方向补画1/4个半径无穷大的圆。又由于Nyquist曲线相对实轴有对称性，可见在ω∈(-∞,+∞)范围内Nyquist曲线绕临界点(-1,j0)顺时针转过两圈，所以此时无论我们如何选取ζ，k和τ的值，系统都不稳定。

取ωn=1,k=1,τ=1,ζ=1时，闭环系统的单位阶跃响应曲线如图12所示。

3) 当ζ<0时，开环传递函数在右半s平面有一个极点，由Nyquist稳定判据可知闭环系统稳定的充要条件是Nyquist曲线逆时针包围临界点(-1,j0)一圈。

(26)

(27)

此时系统的Nyquist曲线如图13所示。

由于开环传递函数包含一个积分环节，我们可以从与频率0+对应的点开始逆时针方向补画1/4个半径无穷大的圆。又由于Nyquist曲线相对实轴有对称性，可见在ω∈(-∞,+∞)范围内Nyquist曲线绕临界点(-1,j0)顺时针转过两圈或不围绕，也可能顺时针穿越临界点，所以此时无论我们如何选取ζ，k和τ的值，系统都不稳定。

取ωn=1,k=1,τ=1,ζ=-1时，闭环系统的单位阶跃响应曲线如图14所示。

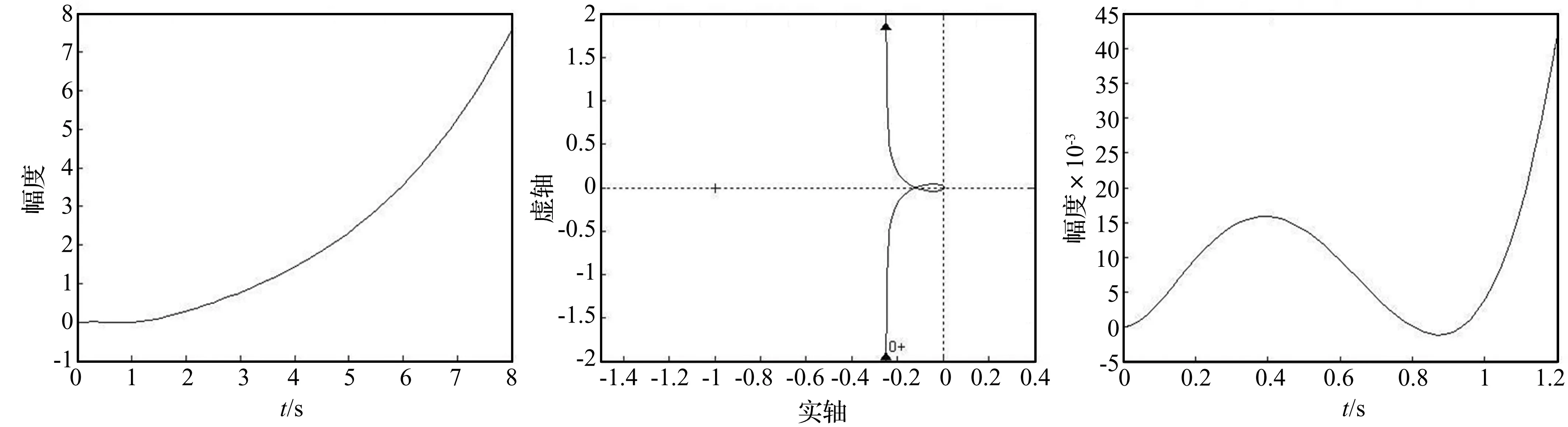
图12 正反馈ζ=1时系统的单位阶跃响应

4 结 论

时滞是整个控制领域中普遍存在的现象。在众多考虑时滞效应的研究工作中，控制系统的稳定性以及失稳机制是两个基础性的研究问题。本文针对被控对象具有二阶系统标准形式的一类振荡系统进行了稳定性分析，分别讨论了闭环系统为单位负反馈和单位正反馈时，时滞对控制系统性能的影响。

分析结果表明对于这种如图1所示结构的典型二阶振荡系统，时滞对该闭环控制系统的稳定性是不具有正面作用的。由于被控对象具有二阶系统标准形式，所以本文的研究具有普遍的意义，并为进一步分析和研究更复杂结构的时滞控制系统打下了基础。

参 考 文 献

[1]张瑞军, 张明勤, 秦英林. 闭环时滞滤波器消除二阶振荡系统残留振动的仿真研究 [J]. 振动与冲击, 2007, 26(11): 163-165.

ZHANG Rui-jun, ZHANG Ming-qin, QIN Ying-lin. Simulation study on closed-loop time-delayed filter for eliminating residual vibration of two-order oscillation systems [J]. Journal of Vibration and Shock, 2007, 26(11): 163-165.

[2]Wang B, Wu X Y. A new high precision energy-preserving integrator for system of oscillatory second-order differential equations [J]. Physics Letters A, 2012, 376(14): 1185-1190.

[3]Wu X Y, You X, Shi W, et al. ERKN integrators for systems of oscillatory second-order differential equations [J]. Computer Physics Communications, 2010, 181(11): 1873-1887.

[4]von Wangenheim L. On the barkhausen and Nyquist stability criteria [J]. Analog Integrated Circuits and Signal Processing, 2011, 66(1): 139-141.

[5]Fan L L, Miao Z X. Nyquist-Stability-Criterion-Based SSR Explanation for Type-3 Wind Generators [J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 807-809.

[6]李国宾, 黄业华, 魏海军. 基于Nyquist稳定判据的磨合过程稳定性研究 [J]. 摩擦学学报, 2012, 32(4): 325-331.

LI Guo-bin, HUANG Ye-hua, WEI Hai-jun. Stability Characteristics of Running-in Process Based on Nyquist Stability Criterion [J]. Tribology, 2012, 32(4): 325-331.

[7]Kazemy A, Farrokhi M. Robust Absolute Stability Analysis of Multiple Time-Delay Lur’e Systems With Parametric Uncertainties [J]. Asian Journal of Control, 2013, 15(1): 203-213.

[8]Kar T K, Jana S. Stability and bifurcation analysis of a stage structured predator prey model with time delay [J]. Applied Mathematics and Computation, 2012, 219(8): 3779-3792.

[9]Wang B, Shi P, Wang J, et al. Novel LMI-based stability and stabilization analysis on impulsive switched system with time delays [J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2012, 349(8): 2650-2663.

[10]Abdallah C, Dorato P, Benitez-Read J, et al. Delayed positive feedback can stabilize oscillatory systems [C]. Proc. of American Control Conference. San Francisco, CA, 1993, June, 2-4.

[11]Wang Z H, Hu H Y. Stability switches of time-delayed dynamic systems with unknown parameters [J]. Journal of Sound and Vibration, 2000, 233(2): 215-233.

[12]Tang G Y. Stabilization for Simple Systems via Delayed Proportional Controller [C]. Proc. of the 6th World Congress on Intelligent Control and Automation. Dalian, China, 2006, June, 21-23.