模型缩聚法在桁架结构损伤识别中的应用

潘晓威，方有亮，毛卓能

(河北大学建筑工程学院，河北保定071002)

1 损伤识别简介

损伤识别技术是当前土木工程领域研究的难点和热点问题，它的基本思想是利用健康结构的数学模型和振动实验数据与损伤结构的振动响应进行比较，从而判定结构损伤位置及程度[1]。我们知道，凡是需要用到实测模态信息的损伤识别方法都要求实测模态的自由度与有限元模型的自由度数一致。而实际测量中会因为比如传感器数量、结构的某些部位难以布置传感器或者某些自由度无法测量的原因，造成实测自由度与数值模拟自由度的不匹配。为了解决实测自由度少于有限元模型自由度数的问题，通常都采用模型缩聚或振型扩充方法。前者是将有限元模型的自由度缩聚到结构测试自由度，即模型缩聚，后者是将结构测试自由度扩充至与有限元模型自由度一致，即模态扩展[4]。本文利用改进的Guyan缩聚法[5]对一平面桁架结构进行模态分析，然后用曲率模态方法[2]对该平面桁架结构进行损伤识别。

2 曲率模态法

由材料力学理论可知，对于梁类构件，曲率是抗弯刚度的函数，它与抗弯刚度成反比，结构发生局部损伤处的抗弯刚度会降低，所以曲率函数在损伤处会突变，根据曲率函数的突变可以进行结构损伤识别。曲率一般不能直接测量，其计算通常采用中心差分法求得，如式(1)所示。

y″=(yi+1-2yi+yi-1)/l2

(1)

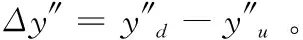
3 改进的Guyan缩聚法

设一个n自由度系统的刚度矩阵为K，质量矩阵为M，特征值和特征向量为λj和φj(j=1～n),其中振型φj可表示为：

(2)

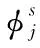
(3)

由式(3)的第2式可得：

(4)

因为Guyan缩聚法[3]略去了惯性量，所以对于Guyan缩聚法只有当被缩减的自由度对应的质量很小时才较精确，若被缩减的自由度有较大质量则该方法有较大误差。本文利用改进的Guyan缩聚法，将式(4)按Nummman级数展开得：

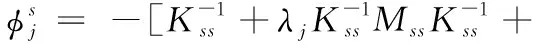
(5)

其中“ο”表示高阶无穷小。将式(5)省略高阶项得：

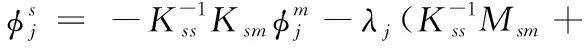
(6)

由式(3)的第1式可得：

(7)

对于许多结构的有限元模型而言，质量矩阵通常采用对角矩阵，那么有

Mms=Msm=0

(8)

式(8)代入式(7)并整理可得：

(9)

式(8)、式(9)代入(6)整理可得：

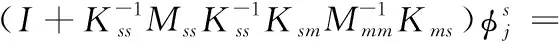
(10)

由式(10)可得：

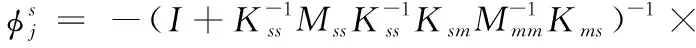
(11)

故改进的缩聚公式为：

(12)

即转换矩阵T为：

(13)

式(12)和式(13)代入式(3)可得：

KTφmj=λjMTφmj

(14)

式(14)两边各乘TT可得：

TTKTφmj=λjTTMTφmj

(15)

令

Kr=TTKT

(16)

Mr=TTMT

(17)

则缩聚后的特征方程为：

Krφmj=λjMrφmj

(18)

显然，Kr和Mr的阶数比原来的K和M减小了，式(18)即可得到缩聚后的各阶频率和振型。

4 数值算例

4.1 方法验证

本文计算模型采用如图 1所示两端固定的平面桁架结构。模型全长跨度c=18m,高h=4m，节点数为12个，杆单元21个。杆单元截面积为A=2 800mm2，材料密度为ρ=7 850kg/m3，弹性模量为E=2.1×1011Pa。

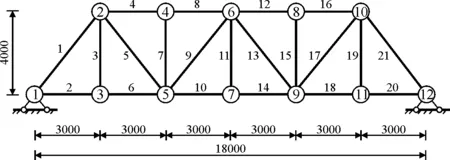
图 1 平面桁架结构模型(单位： mm)

采用ANSYS软件对结构进行模态分析所得到的前五阶振型及频率如图2所示。

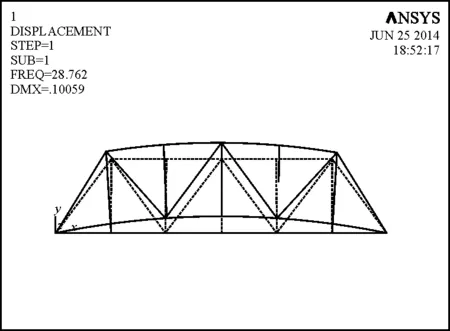
(a)一阶模态振型(频率 28.762 Hz)

(b)二阶模态振型(频率 56.927 Hz)

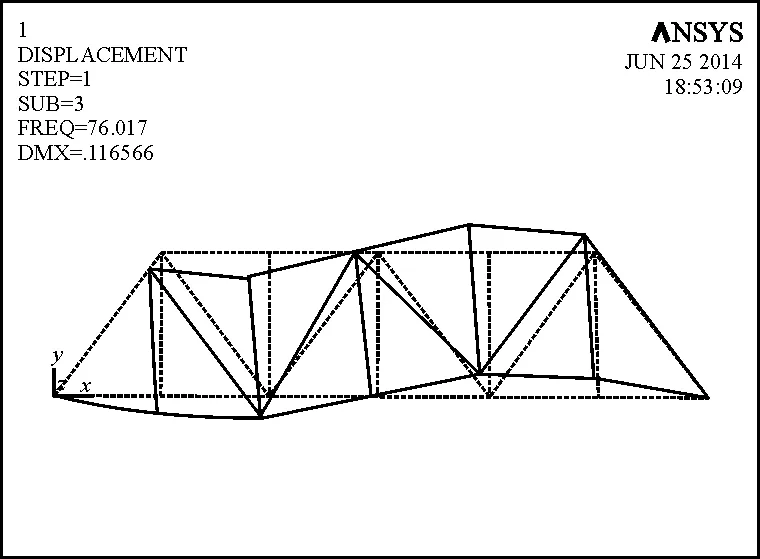
(c)三阶模态振型(频率 76.017 Hz)

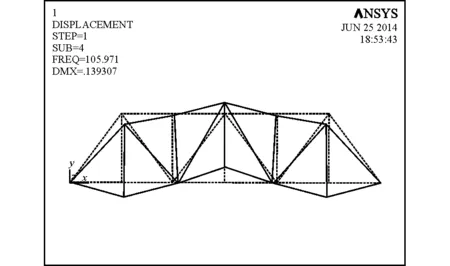
(d)四阶模态振型(频率 105.971 Hz)

(e)五阶模态振型(频率 141.268Hz)图2 桁架结构各阶模态振型及频率

利用改进的Guyan缩聚法缩聚其每一节点的水平自由度，得到前五阶频率，其结果如表 1所示。

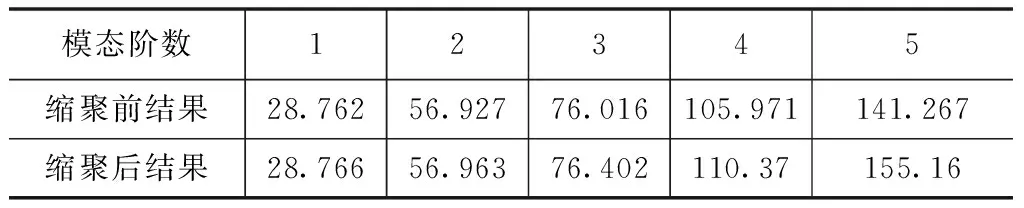
表1 前五阶频率结果比较

从上表中可以看出在平面桁架结构中，利用改进的Guyan缩聚法缩聚水平自由度能够得到很精确的结果，误差非常小。

4.2 损伤识别

利用改进的Guyan缩聚法，缩聚掉每一个节点的水平自由度达到实测自由度与理论自由度相匹配，为简化计算，仅考虑模型主振型方向，计算下弦节点的曲率模态。曲率计算采用中心差分法。损伤单元采用减小弹性模量E来模拟，假定该桁架结构第6号单元损伤25 %，计算过程如表 2所示。

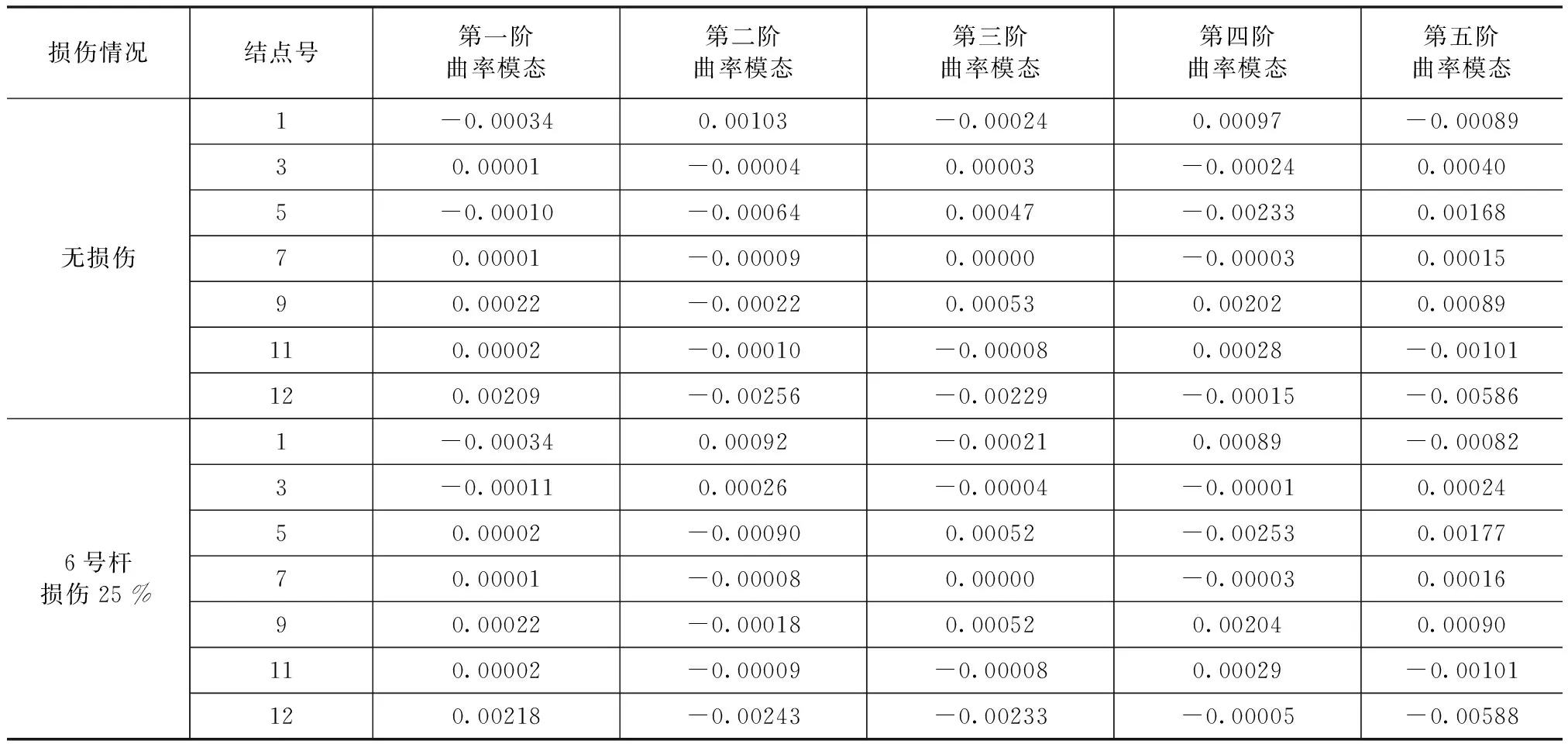
表2 杆单元无损伤和损伤时各阶曲率模态

6号杆损伤时，利用Matlab软件编程计算，其曲率模态变化量如下图3所示。

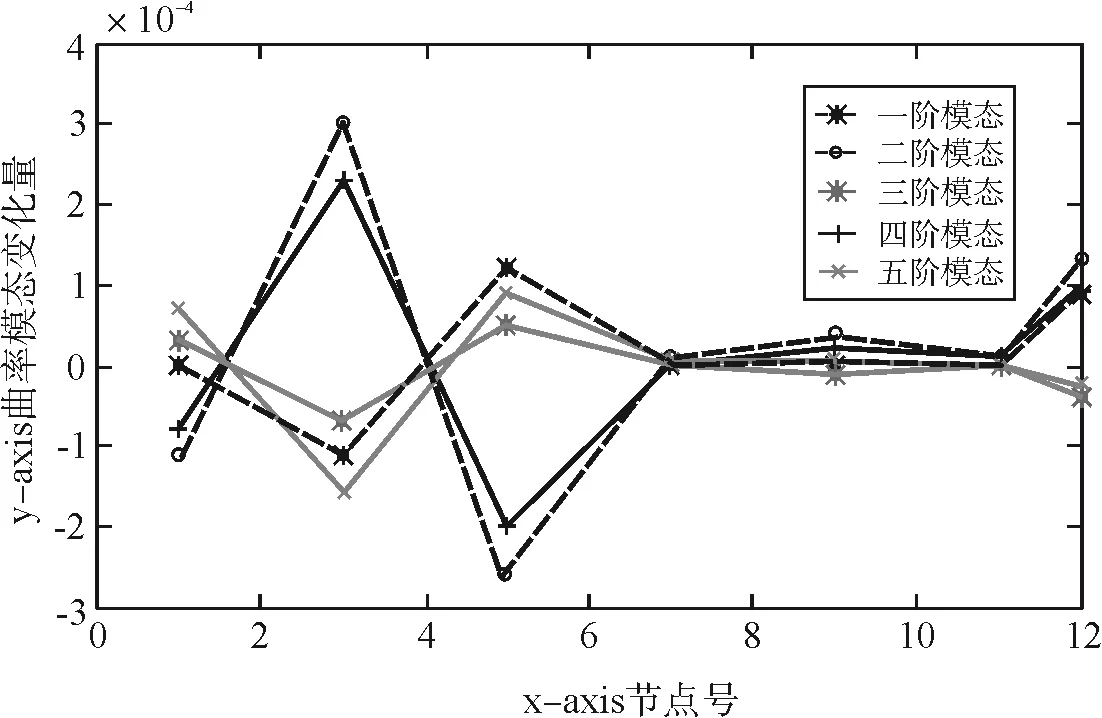
图3 桁架6杆单元损伤25 %时的曲率模态变化量

从图3中可以看到，6号杆的端节点3和5处的曲率模态发生突变，从而可以判定杆件的损伤。同时，可观察到，对于6号杆的损伤，各阶均有较好的识别效果，其中二阶曲率模态变化最突出，识别效果最好。

5 结论

本文利用改进的Guyan缩聚法缩聚平面桁架结构的水平自由度达到实测自由度与理论自由度相匹配，通过数值模拟计算对该平面桁架结构进行损伤识别，结果表明：

(1)采用改进的Guyan缩聚法缩聚其水平自由度得到的频率的数值很准确，误差很小。由于该方法是对质量矩阵和刚度矩阵进行缩聚，因此只有在缩聚的自由度质量很小，而刚度很大时才比较合理。此外，随着频率的增大，误差将变大，所以该方法适用于分析低阶模态。

(2)利用改进的Guyan缩聚法进行自由度匹配后可进行杆单元的损伤识别。

[1] 刘伟，高维成，孙毅.自由度匹配技术在网壳结构损伤识别应用中的比较研究[J].振动与冲击，2007，(2)

[2]PandeymBiswas,Sammanmm.Damagedetectionfromchangesincurvaturemodeshapes[J].JournalofSoundandVibration,1991,145 (2):321-332

[3]R.JGuyan.ReductionofStiffnessandmassmatrices[J].AIAAJournal.1965,13(1):380

[4]J.CO’Callahan.AProcedureforImprovedReducedSystem(IRS)model[J].In:AlfredLW,DominickJ,Demichele,eds.Proceedingsofthe7thInternationalmodalAnalysisConference,LasVegas,1989-02-20-22.Kissimmee:UnionCollege.1989:17-21

[5] 杨秋伟，刘济科.一种改进的模型缩聚方法[J].力学与实践,2006,28(2)