“土力学”课程教学中学习迁移应用初探

刘纪峰,张会芝

1.三明学院建筑工程学院,福建三明,365004；2.College of Engineering,Michigan State University, MI 48823,USA

“土力学”课程教学中学习迁移应用初探

刘纪峰1,2,张会芝1

1.三明学院建筑工程学院,福建三明,365004；2.College of Engineering,Michigan State University, MI 48823,USA

“土力学”课程包括的知识点多而且分散，其中大部分的知识点需要繁琐的公式推导和计算，但该课程的学时又非常有限，为了使学生在有限的学时内理解掌握相关知识点，就要求教师学习应用学习正迁移。应用土体三相体系草图和相关概念推导其压缩变形公式、利用直角坐标系下斜率概念和土体固结历史推导其不同条件下的固结变形公式、利用莫尔应力圆推导推导土体极限平衡条件等这些学习迁移的案例，概念明确、形象直观，便于学生理解掌握，可为“土力学”课程教学提供参考、借鉴。

土力学；课程教学；学习迁移；案例

学习迁移就是“一种学习对另一种学习的影响”。学习是一个连续的过程，学习者通常根据已经具有的知识经验、认知结构、动作技能等基础进行，这种已有的知识结构对新知识学习的影响就形成了知识的迁移[1]。学习迁移包括正迁移和负迁移，前者是指一种经验的获得对另一种学习起促进作用，一般所说的迁移都是指正迁移[2]。

土力学是土木工程和相关专业的专业基础课，主要讲授土的物理性质，土的应力、应变、强度关系及其力学计算模型，并采用数学力学方法求解各种条件下土体中的应力分布、变形特征、土压力和地基承载力、边坡稳定性分析等，该课程在本学科中具有连接一般基础课和专业课的重要作用[3-5]。该课程设置为34个学时(其中包括6学时的实验课)，具有理论性强、公式推导多、知识点多且内在联系不强等特点，在教学过程中，不可避免地出现授课内容多、计算公式繁、上课时数少等矛盾，如何在教学大纲规定的学时数里让学生对土力学的相关内容有较好的掌握，成为任课教师需要认真思考的问题。基于学习迁移理论，本文介绍了利用土体三相体系草图和相关概念推导压缩变形公式、利用直角坐标系下的斜率和土体固结历史推导其不同条件下的固结变形公式、利用莫尔圆推导土体强度准则三个学习迁移案例，以期抛砖引玉。

1 由三相体系草图推导土体压缩变形公式

在土力学中，通常用三相草图来表示土的三相组成，即土颗粒(固体)、水和空气。通过三相草图，可以直观形象地计算土体物理性质的指标。土中孔隙含量可用孔隙比e表示，其定义为孔隙(水+空气)体积与土颗粒体积之比，即e=Vv/Vs。基于以上概念，设某某长度为H的土试样中土颗粒的体积Vs=1，根据孔隙比的定义，则其初始孔隙比e0=Vv/Vs=Vv/1=Vv，假定受力后压缩变形值为ΔH，对应的孔隙比变化为Δe(图1)。

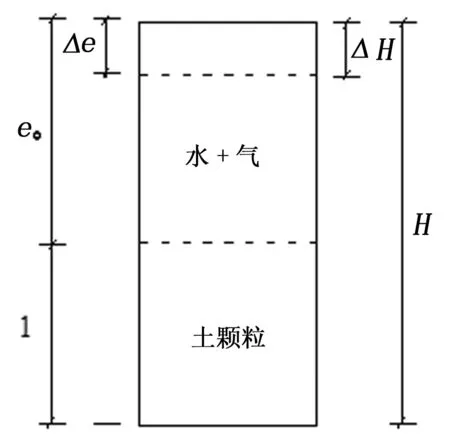
图1 土的三相体系草图

由图1可知：

ΔH·(1+e0)=Δe·H

(1)

将式1变形后可得：

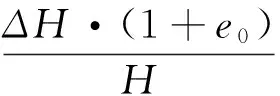
(2)

或

(3)

2 由二维坐标系下的斜率概念推导土体固结公式

如图2所示的平面直角坐标系，直线AB段的斜率为S1，AB上一段到B点的斜线在Y轴上的截距为ΔY1，在X轴上的截距为ΔX1；直线BC段的斜率为S2，BC上一段直线Y轴上的截距为ΔY2，在X轴上的截距为ΔX2，根据斜率概念，可知：

ΔY=ΔY1+ΔY2=S1·ΔX1+S2·ΔX2

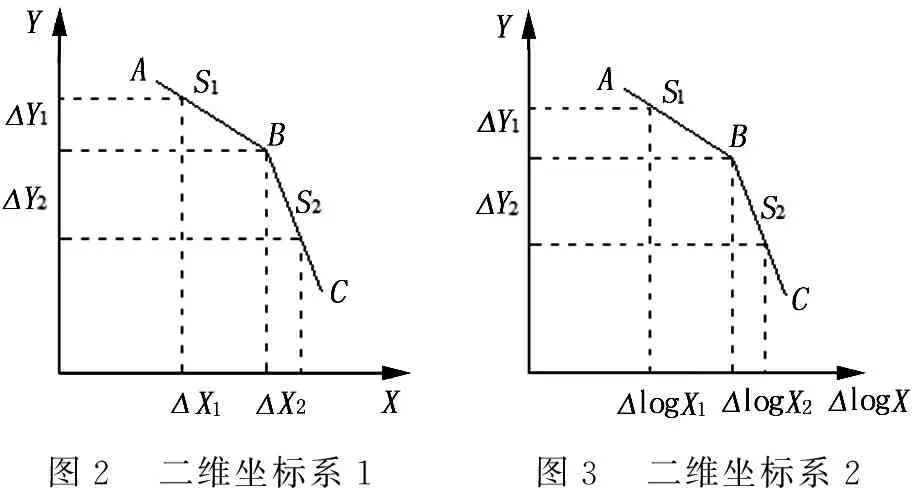
(4)

如将平面直角坐标系的X轴坐标换为对数坐标，AB、BC上两段直线在logX轴上的截距分别为ΔlogX1和ΔlogX2，则有：

ΔY=ΔY1+ΔY2=S1·ΔlogX1+S2·ΔlogX2

(5)

Δe2=Cc·(logP4-logP3)=Cc·log(P4/P3)

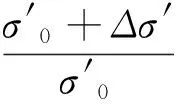
(6)

将式(3)代入式(6)，可得正常固结土的固结沉降公式为：

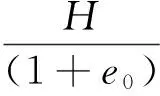
(7)

对于欠固结土，其推导过程相似，具体计算式与(7)类似，为：

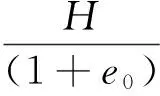
(8)

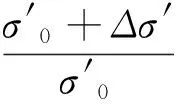
相应的固结沉降公式为：

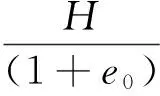
(9)

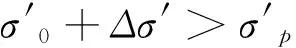
图4 e-logP坐标系1 图5 e-logP坐标系2 图6 e-logP坐标系3

(10)

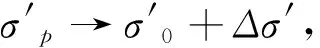
(11)

联合式(3)、式(10)、式(11)可得：

(12)

实际应用时，对于较厚的土体，其自重应力是随深度增加的，为提高计算精度，可将土体分层进行计算，根据土体固结状态不同，根据式(7)、式(8)、式(9)或式(12)，分别计算各分层土体的固结沉降值，再对计算结果累加求和，即可得到各《土力学》教材中常用的计算公式[6]，限于篇幅，不再详细推导。

3 由莫尔应力圆推导土体极限平衡条件

如图7所示的微元体，厚度取为1，可按平面问题计算，设其任意斜截面与大主应力面即水平面成α角，斜截面上作用法向应力σ和剪应力τ，根据理论力学中的静力平衡条件，可得：

∑x=0⟹σ·sinα·ds-τ·cosα·ds-σ3·sinα·ds=0

(13)

∑y=0⟹σ·cosα·ds+τ·sinα·ds-σ1·cosα·ds=0

(14)

图7 任意斜截面上的应力计算示意图

联立(13)和(14)两式，可求得任意截面上的法向应力σ和剪应力τ：

(15)

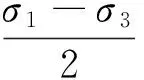
(16)

式中，σ为与大主应面成α角的截面上的法向应力，kPa；

τ为同一截面上的剪应力，kPa。

由前两式平方并相加，整理得：

(17)

在σ-τ坐标系中，上式表示圆心为[(σ1+σ3)/2,0]，半径为(σ1-σ3)/2的圆的方程，根据莫尔-库仑破坏理论，土体达到极限状态时强度与莫尔圆相切，无粘性土的极限平衡状态如图8所示，粘性土的极限平衡状态如图9所示。

3.1 无粘性土的极限平衡条件

如图8所示，莫尔圆的半径为(σ1-σ3)/2，根据三角函数关系式，有：

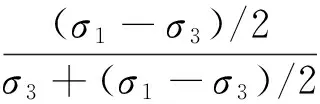
=σ1sinθ+σ3sinθ

⟹σ1(1-sinθ)=σ3(1+sinθ)

(18)

同理可推导出：

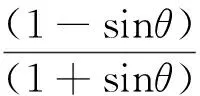
(19)

3.2 粘性土的极限平衡条件

如图9所示，莫尔圆的半径为(σ1-σ3)/2，强度包线在τ轴上的截距为c，易知A1O=ccotφ，根据三角函数关系式，有：

⟹⟹σ3(1+sinθ)

=σ1(1-sinθ)-2ccotφ

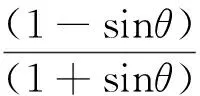
(20)

式中，KA=tan2(450-φ/2)。

(21)

式中，Kp=tan2(450+φ/2)。

式(18)、(19)为无粘性土的极限平衡条件，式(20)、(21)为粘性土的极限平衡条件。式(18)～(21)中，σ1为土体自重应力，σ3为土体侧向压力，其相关计算方法在前面已论述。式(18)～(21)在后面章节的挡土墙背后的土压力计算将会有进一步的应用。

4 结束语

“土力学”课程经验性较强，知识点分布多而散乱，且各知识点之间联系不紧密，缺乏系统性和连贯性，受制于学时等多方面因素限制，如果按部就班地讲授，常常出现要么相关知识点很难讲深讲透，要么就是课上不完，只能挑选一些重点章节讲解，造成学生理解和掌握相关内容时非常吃力，甚至会因此丧失对该门课程的学习兴趣。

“土力学”教学过程中牵涉到三角函数、直角坐标系应用、材料力学等诸多先修课程的知识，在课时安排非常有限的情况下，如何教会学生需要了解和掌握的各知识点，就需要任课教师多加思考，合理地利用先修课程的相关基本知识，增加它们同土力学各公式之间的联系，形成积极的学习迁移，对于更好地理解和掌握土力学课程的众多知识点和其工程应用具有十分重要的意义。以上仅讨论了在土力学教学过程中用到的实现学习迁移的一些具体例子，更多的方法还需要在以后的教学实践中不断地摸索。

[1]张玲.浅谈知识迁移对大学英语教学改革的影响[J].现代交际,2012(7):204-205

[2]赵志峰,邵光辉,张婷.浅议如何在“基础工程”教学中实现学习迁移[C]//第九届全国高校土木工程学院(系)院长(主任)工作研讨会论文集,北京：科学出版社，2008:273-276

[3]刘纪峰,张会芝.“土力学”课程教学内容和方法的一些体会[J].中国电力教育,2011,25:115-116

[4]刘纪峰,张会芝.“土力学”课程教学中培养学生综合能力的方法初探[J].中国电力教育,2011,19:86-87

[5]王伟,陶菲菲,卢廷浩,等.启发式教学在土力学教学中的应用[J].高等建筑教育,2008,17(5):83-86

[6]陈希哲.土力学地基基础[M].4版.北京:清华大学出版社,2004:114-118

(责任编辑：刘小阳)

2014-06-15

福建省教育厅“福建省高等学校学科带头人培养计划项目”(FETU);三明学院教育教学改革项目“与国家标准相衔接的课程与教学内容体系探索——以《基础工程》为例”(J1311/Q)。

刘纪峰(1979-),河南沈丘人,博士,副教授,主要研究方向:城市地下工程。

10.3969/j.issn.1673-2006.2014.09.035

G640

A

1673-2006(2014)09-0115-04