最大熵产生原理在非平衡凝固中应用

王 慷，王海丰，刘 峰

(西北工业大学 凝固技术国家重点实验室， 陕西 西安 710072)

1 前 言

熵及熵产生概念是平衡及非平衡体系理论研究的基础。由热力学第二定律可知，孤立的非平衡体系向平衡态演化过程中，熵总是趋向于最大值[1-2]，即能量最低态对应于平衡态。与此类似，最大熵产生原理(Maximum Entropy Production Principle, MEPP)认为非平衡体系演化时总是使熵产生最大化[3]。对于孤立非平衡体系的演化，在任意给定时间间隔内，熵产生总是达到最大，因而体系达到平衡态时熵也达到最大。简言之，孤立非平衡体系演化时，总是选择最短路径或最快方式趋向于平衡[3]。目前，该原理被认为是描述非平衡耗散体系的普适性原理[3-4]，熵产生率最大情形即对应体系的演化方程。

(1)

(2)

其中qi(Ji)=JiXi(Ji)，为过程i耗散的自由能。而MEPP的数学形式如式(3)所示[3,5,7]：

(3)

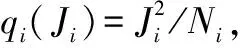
非平衡凝固过程中，伴随体系自由能耗散，亚稳态过冷液相向固相转变属于典型非平衡演化体系。以往凝固理论多采用诸多假设，例如，研究界面条件时经常采用局域平衡假设，对扩散过程的描述常采用菲克扩散定律[12]。这些假设限制了模型的适用范围，如局域平衡假设只适用于近平衡凝固，菲克扩散定律只能描述局域平衡且组元间无相互作用的扩散过程[7,13]。因而，将MEPP应用到快速凝固过程中，可从自由能耗散角度对凝固过程给出更普适的描述。

基于以上考虑，Liu和Wang等将MEPP用于描述非平衡凝固体系演化[7,11,13-15]，得到更普适的演化方程，进一步讨论了体系动力学过程。本文将对这些工作进行综述。并依次介绍MEPP在二元合金中的应用，包括尖锐和弥散界面动力学[7,11]，及该原理在三元合金中的应用，包括界面动力学[13]、界面稳定性[14]及自由枝晶生长理论[15]。最后对MEPP的应用进行展望。

2 最大熵产生原理在二元合金凝固中应用

针对二元合金凝固过程的已有理论中，大多假设局域平衡、稀溶液及线性液固相线[12]。这些假设对浓溶液合金的非平衡凝固过程是不适用的，只有基于(拓展)不可逆热力学，并耦合热力学数据库，才能对二元非平衡凝固体系给出更精确的描述[7]。基于MEPP，将分别介绍作者课题组研究建立的二元合金尖锐界面动力学模型及多相场模型，进而分析界面动力学过程。

2.1 尖锐界面动力学

这里处理二元A-B合金在封闭系Ω中的凝固情形，平直界面以速度V从固相向液相移动。为简化问题，不考虑两组元的摩尔体积差，均用Vm表示。根据拓展不可逆热力学理论，局域非平衡条件下体系的自由能密度g可表示为式(4)[7]：

(4)

其中xB为B组元的摩尔百分比，μA与μB为A、B组元的化学势，αk=(Vm/(VDk)2)(∂μk/∂xk)。

由于存在约束关系xA+xB=1及JA+JB=V/Vm，此时体系中只有一个成分及扩散通量是独立变化的。由于尖锐液/固界面的存在，体系的Gibbs自由能变化率可表示为式(5)[7,16]，

(5)

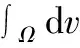
(6)

其中,

(6a)

(6b)

可见，体系Gibbs自由能耗散可分为两部分，即块体相耗散和界面处耗散。凝固过程中，体系自由能耗散可分为界面处和块体相；界面处耗散分为界面迁移及界面互扩散，块体相中只有组元扩散耗散能量。因此，体系的耗散函数可写为式(7)和式(8)[7]：

(7)

(8)

(9)

(10)

整理后可得式(11)，(12)，(13)，

(11)

JC=RTMC×

(12)

(13)

式(11)是考虑局域非平衡效应后二元合金在块体相的扩散方程；式(12)，(13)是局域非平衡界面动力学模型，分别对应界面迁移方程和溶质截留方程。该模型适用于二元浓溶液合金局域非平衡条件下的非稳态凝固过程，可对Si-9%As(原子百分数)合金非平衡凝固界面动力学过程给出合理描述，并澄清了凝固中是否存在溶质拖拽效应这一理论争议[7]。

2.2 弥散界面动力学

相场模型按自由能密度f形式可分为两类，①Wheeler-Boettinger-McFadden(WBM)模型[17]：f为成分相同、扩散势不同的液/固相混合；②多相场模型[18]：f是成分不同的液/固相混合，其成分确定时采用确定的分配关系或扩散势相等，这样，体系中就多了一个约束条件。相比于WBM模型，多相场模型更容易向多元多相合金拓展。如果能合理解决多相场模型中额外约束问题，此类模型会有广泛的应用前景。下面论述作者课题组基于MEPP建立的多相场模型，相比于前人工作[18]，该模型可自洽地解决多相场模型中额外约束问题。

二元合金非平衡凝固时，多相场体系的约束条件为φS+φL=1，c=hScS+hLcL。体系自由能可表示为式(14)[11,18]：

(14)

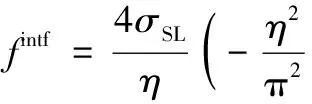
(14a)

(14b)

考虑约束条件，体系的自由能可表示为式(15)[11]：

(15)

此时，体系Gibbs自由能变化率可表示为式(16)[11]：

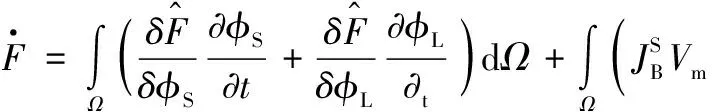
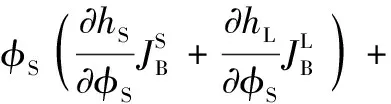
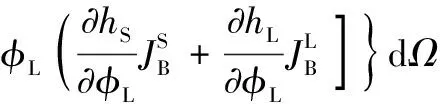
(16)

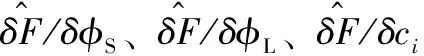
(17)

体系演化遵循式(18):

(18)

体系相场演化方程及扩散方程为：

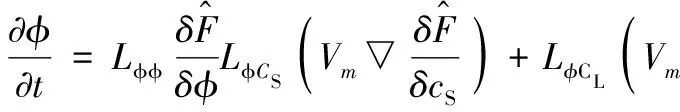
(19)

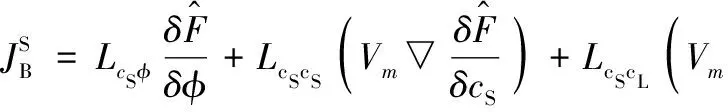
(20)

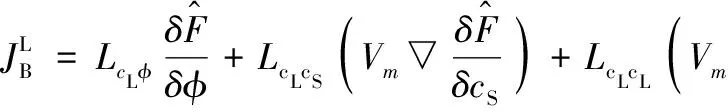
(21)

其中动力学系数见文献[11]。从MEPP得到多相场模型热力学自洽且动力学系数遵循Onsager倒易关系。相比于前人工作[18]，当前多相场模型可合理地解决多相场模型中体系额外约束问题，并对凝固过程中界面和块体中自由能耗散机制给出了合理描述。

3 最大熵产生原理在多元合金中应用

凝固理论研究主要集中于二元合金，但是工业应用合金主要为多组元[13]。因此，凝固理论能否用于工业生产取决于多元合金凝固理论的发展。本部分将MEPP应用于多元合金非平衡凝固，建立界面动力学模型，并基于此建立平界面稳定性模型和自由枝晶生长模型。

3.1 多元合金界面动力学

与二元合金凝固相比，多元合金中需处理多组元溶质守恒的约束问题。对于n组元置换固溶体合金非平衡凝固情形，忽略组元摩尔体积差别，体系Gibbs自由能密度可表示为式(22)[13]：

(22)

其中非平衡系数αk=(Vm/(VDk)2)(∂μk/∂xk)，VDk为k组元扩散速度。采用式(4)～(6)相同方法，体系Gibbs自由能变化率[13]表示为式(23)和式(24)：

(23)

(24)

类似地，体系耗散函数[13]表示为式(25)和式(26):

(25)

(26)

块体相与界面处的变分原理分别表示为式(27)和式(28)：

(27)

(28)

整理后可得式(29～31)[13]:

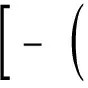
(29)

(30)

(31)

式(29)为考虑组元间相互作用及局域非平衡效应的多元扩散方程；式(30)和式(31)为局域非平衡条件下多元合金界面动力学模型，包括界面速度方程和溶质截留模型。该模型基于拓展不可逆热力学建立，因而适用于多元合金的极端非平衡凝固过程。在计算中可方便地耦合热力学数据，从而反映浓溶液合金中组元间相互作用及其对相变动力学过程的影响。模型应用表明，多元浓溶液合金中组元间相互作用，可促使溶质截留系数随界面迁移速率非单调变化[13]。

3.2 平界面稳定性

凝固过程中，界面失稳组织形成各种形貌，界面稳定性研究是理解组织形成过程的关键。下面基于式(29～31)的界面动力学模型，分析多元合金快速定向凝固中平界面稳定性。由于式(29)多元扩散方程中动力学系数Ak不是常数，而与体系温度、成分相关，使用该方程难以得到扩散场的解析表达式，因此，描述块体相时采用修正的扩散方程[14]如式(32)：

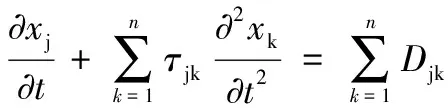
(32)

其中Djk为扩散矩阵元素，τjk=Djk/V2Dj为k组元对j组元弛豫时间的影响。显然，该方程通过扩散矩阵非对角线项考虑组元扩散过程中相互作用，且通过弛豫时间考虑局域非平衡效应，因而适用于多元浓溶液合金非平衡凝固过程中扩散过程的描述。由于体系温度场弛豫时间，即使在极端非平衡凝固条件下，远小于溶质扩散场弛豫时间，因而，对于温度场的描述仍采用经典傅利叶导热定律[13-14]。

对于平界面稳定性分析，仍采用经典Mullins和Serkerka的线性分析思路[19]，即平直的液/固界面处于稳态时发生正弦形式的扰动，Z=φ(X,t)=δ(t)×sin(ωX)。这一扰动引起界面速度、成分和温度发生变化，其变化量与扰动成正比。经过分析得到稳定性判据可表示为式(33)[14]：

Sn(ω)=-Γω2-(KSGSξS+KLGLξL)+

(33)

关于变量含义及表达式可参考文献[14]。在定向凝固中，上式前两项为负，第3项为正，即定向凝固中界面能项、温度梯度使界面稳定，而界面前沿溶质扩散使界面趋向于失稳。针对临界稳定情形，使用式(33)可预测给定凝固条件下，促使界面失稳的临界成分，并澄清其稳定性机制[14]。由于定向凝固技术是制备具有定向组织铸件的重要手段，因而，当前结果可对该过程中合金成分设计提供指导。

3.3 自由枝晶生长

枝晶是最常见的凝固组织之一，其形态对铸件最终力学性能有重要影响。枝晶生长理论的研究重点在于预测枝晶尖端形貌、生长动力学过程等，其中应用最广泛的理论将临界稳定性分析与Ivantsov解[12]相结合，即使用临界稳定性分析得到临界失稳波长，以此近似枝晶尖端半径，再结合Ivantsov解，得到枝晶尖端浓度场和温度场的解，以此为框架得到枝晶尖端生长参量与凝固条件的关系。下面基于式(29～31)的界面动力学模型和式(33)的临界稳定性判据，建立自由枝晶生长模型。根据Langer和Müller-Krumbhaar[20]分析，枝晶尖端半径可采用界面临界失稳波长来近似，可表达为式(34)[15,20]：

Sn(2π/R)=0

(34)

其中R为枝晶尖端曲率半径。对于稳态枝晶生长, 假定枝晶尖端近似为旋转抛物面，则枝晶尖端浓度场和温度场可表示为式(35)和式(36)[15]:

(35)

(36)

4 结 语

作者课题组近几年将MEPP应用于非平衡凝固理论研究所取得的成果，相比前人对MEPP在凝固方面的应用存在以下优点：①基于该原理建立的模型可对体系自由能耗散机制给出更清晰地描述；②模型可对非平衡凝固中界面动力学、界面稳定性及枝晶生长等不同演化过程给出更合理描述；③该原理中采用拉格朗日乘子法可合理考虑体系约束，进而更适合于描述复杂非平衡凝固体系的演化。虽然MEPP在非平衡凝固中已取得一定成功，但已有的凝固理论与工业生产条件存在一定差距。故其应用受到局限，研究者仍需深入探索、不断完善。我们对该原理未来的研究方向寄予如下期望：①多相场模型是描述凝固过程的强有力工具，但由于多元多相合金非平衡凝固过程中体系复杂性限制，多相场模型在工业多元多相合金中的应用发展缓慢，MEPP的应用可促进该问题的解决；②当前凝固理论中大多忽略组元间摩尔体积差，相应理论只适用于置换固溶体合金，而间隙组元在工业合金中普遍存在，MEPP的应用有望合理描述凝固过程中置换及间隙组元的不同行为。

参考文献 References

[1] Lin Zonghan (林宗涵).ThermodynamicsandStatisticalPhysics(热力学与统计物理) [M]. Beijing: Peking University Press，2007：39-68.

[2] Jiang Qing (蒋 青), Wen Zi (文 子).ThermodynamicsofMaterials(材料热力学)[M]. Beijing: Higher Education Press，2011：1-34.

[3] Martyushev L M, Seleznev V D. Maximum Entropy Production Principle in Physics, Chemistry and Biology [J].PhysicsReports, 2006(426):1- 45.

[4] Fratzl P, Fischer F D, Svoboda J. Energy Dissipation and Stability of Propagating Surfaces [J].PhysicalReviewLetters, 2005(95): 195702.

[5] Onsager L. Reciprocal Relations in Irreversible Processes[J].PhysicalReview, 1931 (15):405-426.

[6] Ziegler H.AnIntroductiontoThermomechanics[M]. Amsterdam: North-Holland, 1983.

[7] Wang H F, Liu F, Zhai H M,etal. Application of the Maximal Entropy Production Principle to Rapid Solidification: A Sharp Interface Model [J].ActaMaterialia, 2012(60):1 444-1 454.

[8] Svoboda J, Turek I, Fischer F D. Application of the Thermodynamic Extremal Principle to Modeling of Thermodynamic Processes in Material Sciences [J].PhilosophicalMagazine, 2005(85):3 699-3 707.

[9] Svoboda J, Fischer F D, Fratzl P,etal. Diffusion in Multi-Component Systems with no or Dense Sources and Sinks for Vacancies [J].ActaMaterialia, 2002(50):1 369-1 381.

[10] Svoboda J, Fischer F D, McDowell D L. Derivation of the Phase Field Equations from the Thermodynamic Extremal Principle [J].ActaMaterialia, 2012(60):396-406.

[11] Wang H F, Liu F, Ehlen G J,etal. Application of the Maximal Entropy Production Principle to Rapid Solidification: A Multi-Phase-Field Model [J].ActaMaterialia, 2013(61): 2 617-2 627.

[12] Kurz W, Fisher D J.FundamentalsofSolidification[M]. Zurich: Trans Tech Publications, 1998.

[13] Wang K, Wang H F, Liu F,etal. Modeling Rapid Solidification of Multi-Component Concentrated Alloys [J].ActaMaterialia, 2013(61): 1 359-1 372.

[14] Wang K, Wang H F, Liu F,etal. Morphological Stability Analysis for Planar Interface During Rapidly Directional Solidification of Concentrated Multi-Component Alloys [J].ActaMaterialia, 2014,67:220-231.

[15] Wang K, Wang H F, Liu F,etal. Modeling Dendrite Growth in Undercooled Concentrated Multi-Component Alloys [J].ActaMaterialia, 2013(61): 4 254-4 265.

[16] Fischer F D, Simha N K. Influence of Material Flux on the Jump Relations at a Singular Interface in a Multicomponent Solid [J].ActaMechanics, 2004(171):213-223.

[17] Wheeler A A, Boettinger W J, McFadden G B. Phase-Field Model for Isothermal Phase Transitions in Binary Alloys [J].PhysicalReviewA, 1992,45:7 424.

[18] Steinbach I, Zhang L J, Plapp M. Phase-Field Model with Finite Interface Dissipation [J].ActaMaterialia, 2012(60):2 689.

[19] Mullins W W, Sekerka R F. Stability of a Planar Interface during Solidification of a Dilute Binary Alloy[J].JournalAppliedPhysics, 1964,35:444-451.

[20] Langer J S, Muller-Krumbhaar H. Theories of Dendrite Growth I. Elements of a Stability Analysis [J].ActaMetallurgica, 1978,26:1 681.

[21] Divenuti A G, Ando T. A Free Dendritic Growth Model Accommodating Curved Phase Boundaries and High Peclet Number Conditions [J].MetallurgyandMaterialsTransanctionsA, 1998,29:3 047-3 056.