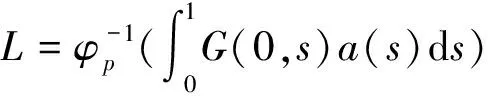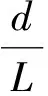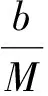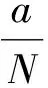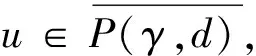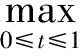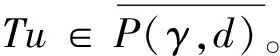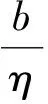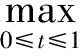带p-Laplacian算子的三阶微分方程边值问题正解的存在性
2014-08-28郭彦平李春景韩迎迎
郭彦平,李春景,韩迎迎
(河北科技大学理学院,河北石家庄 050018)
带p-Laplacian算子的三阶微分方程边值问题正解的存在性
郭彦平,李春景,韩迎迎
(河北科技大学理学院,河北石家庄 050018)
许多不同应用数学和物理领域的研究都可归结为带有p-Laplacian算子的边值问题,因此对此问题的研究具有重要的理论意义和应用价值。本文讨论了带p-Laplacian算子三阶三点边值问题:
的正解的存在性,其中φp(s)=|s|p-2s,p>1。应用Avery-Peterson不动点定理,当非线性项f满足一定的增长条件时,得到上述边值问题至少存在三个正解的充分条件。
p-Laplacian;边值问题;Avery-Peterson不动点定理
1 问题提出
本文讨论带p-Laplacian算子的三阶三点边值问题:
(1)
的正解的存在性,其中φp(s)=|s|p-2s,p>1。
近年来,许多学者都在关注三阶微分方程边值问题,并研究其正解的存在性[1-15]。张立新等在文献[1]中研究了三阶三点边值问题:
其中φp(s)=|s|p-2s,p>1,利用Avery-Peterson不动点定理证明了3个正解的存在性。郭少聪等在文献[2]中讨论了三点边值问题:
3个拟对称正解的存在性,其中α>0,0<η<1,φp(s)=|s|p-2s。通过应用Avery-Peterson不动点定理得到上述边值问题具有3个拟对称正解的充分条件。
在本文中总假设以下条件成立:
H1)0<η<1,0<α<1;H2)f∈C([0,1]×[0,+∞)×R,(0,+∞)),a(t)在[0,1]上非负连续。
2 预备知识
定义1设E是一个赋泛线性空间,P是E中的一个非空闭凸集。若P满足:
1)∀x∈P,λ>0⟹λx∈P;2)x,-x∈P⟹x=0,则P称为E中的一个锥。
定义2一个算子如果连续且映有界集为相对紧集,则称它是全连续算子。
定义3设P是Banach空间E中的一个锥。若映射α:P→[0,∞)连续且∀x,y∈P,∀r∈[0,1],有:
α(rx+(1-r)y)≥rα(x)+(1-r)α(y),则称α是P上非负连续凹泛函。
类似地,若映射β:P→[0,∞)连续且∀x,y∈P,∀r∈[0,1],有:β(rx+(1-r)y)≤rβ(x)+(1-r)β(y),则称β是P上非负连续凸泛函。
令γ和θ是锥P上的非负连续凸泛函,α是P上的非负连续凹泛函,ψ是P上的非负连续泛函,对正数a,b,c,d定义如下凸集:
P(γ,d)={x∈P|γ(x) P(α,b;γ,d)={x∈P|b≤α(x),γ(x)≤d}, P(α,b;θ,c;γ,d)={x∈P|b≤α(x),θ(x)≤c,γ(x)≤d} 和闭集: R(ψ,a;γ,d)={x∈P|a≤ψ(x),γ(x)≤d}。 下面给出Avery-Peterson不动点定理。 α(x)≤ψ(x),‖x‖≤Mγ(x)。 (2) C1){x∈P(α,b;θ,c;γ,d)|α(x)>b}≠∅且对x∈P(α,b;θ,c;γ,d)有α(Tx)>b; C2)对x∈P(α,b;γ,d)且θ(Tx)>c,有α(Tx)>b; C3)0∉R(ψ,a;γ,d)且当x∈R(ψ,a;γ,d),ψ(x)=a时,ψ(Tx) γ(xi)≤d,i=1,2,3;b<α(x1),a<ψ(x2)且α(x2) 引理1设α≠1,则对h∈C[0,1],边值问题: (3) 其中: (4) 所以有: (5) 若t≤η,则由式(5)得: 若t≥η,则由式(5)得: 引理2若条件H1)成立,则对h∈C[0,1],边值问题: (6) 证明令φp(u′)(t)=v(t),则原边值问题可简化为 引理3若条件H1)成立,且h(t)≥0,t∈[0,1],则边值问题(6)的解u(t)满足如下条件: i)u(t)≥0; ii)u(t)在(0,1)上是凹的。 证明i)由于0<η<1,0<α<1,t∈[0,1],则G(t,s)≥0。又由于h(t)≥0,所以u(t)≥0。 在E中定义锥P:P={u∈E:u(t)≥0,u(0)=0,u在(0,1)上是凹的}。 在P上定义非负连续凸泛函γ,θ,非负连续凹泛函α和非负连续泛函ψ如下: 由引理4及前面定义的泛函得:α(u)≤ψ(u),θ(u)≤γ(u), ‖u‖≤γ(u)。 所以定理1的式(2)满足。 引理5假设条件H1)和条件H2)成立,则算子T:P→P是全连续算子。 证明对u∈P,由T的定义及引理3可以得到(Tu)(t)≥0,(Tu)(0)=0,(Tu)(t)在(0,1)上是凹的,所以TP⊂P。用常规方法可以证明T是全连续算子。 定理2假设条件H1)和条件H2)成立,存在正数a,b,d满足a γ(ui)≤d,i=1,2,3;b<α(u1),a<ψ(u2)且α(u2) 证明边值问题(1)有解u=u(t)当且仅当算子方程u=Tu有不动点。下面验证算子T满足Avery-Peterson不动点定理的条件。 由假设A1)得: 这样定理1的条件C1)满足。 这样定理1的条件C2)满足。 因为ψ(0)=0 0≤u(t)≤a, |u′(t)|≤d,t∈[0,1]。 由假设A3)得: 这样定理1的条件C3)满足。 / [1] 张立新,葛渭高.带p-Laplacian算子的三阶微分方程边值问题三个正解的存在性[J].系统科学与数学,2011,31(7):837-844. ZHANG Lixin,GE Weigao.Existence of three positive solutions for third-order differential equations of boundary value problem withp-Laplacian[J].Journal of Systems Science and Mathematical Sciences,2011,31(7):837-844. [2] 郭少聪,郭彦平,陈悦荣.带p-Laplacian算子三点边值问题拟对称正解的存在性[J].数学的实践与认识,2012,42(16):236-240. GUO Shaocong,GUO Yanping,CHEN Yuerong.The existence of pseudo-symmetric positive solutions for three-point boundary value problems withp-Laplacian[J].Mathematics in Practice and Theory,2012,42(16):236-240. [3] FENG Hanying,GE Weigao.Existence of positions for m-point boundary-value problem with one-dimensionalp-Laplacian[J].Nonlinear Anal,2008,68:2017-2026. [4] SUN Yongping.Existence of triple positive solutions for third-order three-point boundary value problem[J].J Comput Math Appl,2008,221:194-201. [5] AVERY R I,PETERSON A C.Three positive fixed points of nonlinear operators on ordered Banach spaces[J].J Comput Math Appl,2001,42:313-322. [6] AVERY R I.A generalization of the Leggett-Willims fixed pint theorem[J].Math Sci Res Hot-line,1998,2:9-14. [7] ANDERSON D R.Multiple positive solutions for a three-point boundary value problem[J].Math Comput Modelling,1998,27(6):49-57. [8] ANDERSON D R.Green's function for a third generalized right focal problem[J].J Math Anal Appl,2003,288(1):1-14. [9] ANDERSON D R,AVERY R I.Multiple positive solutions to a third-order discrete focal boundary value problem[J].Comput Math Appl,2001,42(3/4/5):333-340. [10] BAI Zhanbing,GUI Zhanji,GE Weigao.Multiple positive solutions for somep-Laplacian boundary value problems[J].Journal of Systems Science and Mathematical Sciences,2004,300:477-490. [11] 许晓婕,费祥历.三阶非线性奇异边值问题正解的存在唯一性[J].系统科学与数学,2009,29(6):779-785. XU Xiaojie,FEI Xiangli.Existence and uniqueness of positive solutions for third-order nonlinear singular boundary value problem[J].J Sys Sci & Math Scis,2009,29(6):779-785. [12] 孙忠民,赵增勤.三阶微分方程组边值问题常号解的存在性[J].系统科学与数学,2007,27(6):811-819 SUN Zhongmin,ZHAO Zengqin.The existence of constant-sing solutions of BVPs for third order differential systems[J].J Sys Sci & Math Scis,2007,21(6):811-819. [13] 田元生,刘春根.三阶p-Laplacian方程三点奇异边值问题三个正解的存在性[J].应用数学学报,2008,31(6):1118-1127. TIAN Yuansheng,LIU Chungen.Three positive solutions of three-point singular boundary value problem for a class of third orderp-Laplacian equations[J].Acta Mathematicae Applicatae Sinica,2008,31(6):1118-1127. [14] DU Zengji,GE Weigao,LIN Xiaojie.Existence of solutions for a class of third-order nonlinear boundary value problems[J].Journal of Mathematical Analysis and Applications,2004,294(1):104-112. [15] YAO Qingliu,FENG Yuqiang.The existence of solutions for a third order two-point boundary value problem[J].Appl Math Lett,2002,15:227-232. Existence of positive solutions for boundary value problem of third-order differential equations of withp-Laplacian GUO Yanping, LI Chunjing, HAN Yingying (School of Science,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China) Many researches on the fields of different applied mathematics and physics can be attributed to the boundary value problem withp-Laplacian.So the research on this issue has important theoretical significance and application value.In this paper,we consider the existence of triple positive solutions for third-order differential equation boundary value problems withp-Laplacian whereφp(s)=|s|p-2s,p>1.By using Avery-peterson's fixed point theorem,underfsatisfies cevtain growth conditions,we study the existence of at least three positive solutions for the above boundary value problem. p-Laplacian; boundary value problem; Avery-Peterson's fixed point theorem 2014-04-16; 2014-09-02;责任编辑:张 军 国家自然科学基金(111371120);河北省自然科学基金(A2013208147) 郭彦平(1965-),男,河北张家口人,教授,博士,主要从事微分方程边值问题方面的研究。 E-mail:guoyanping65@sohu.com 1008-1542(2014)06-0524-05 10.7535/hbkd.2014yx05001 O175.8MSC(2010)主题分类34B05 A 郭彦平,李春景,韩迎迎.带p-Laplacian算子的三阶微分方程边值问题正解的存在性[J].河北科技大学学报,2014,35(6):524-528. GUO Yanping,LI Chunjing,HAN Yingying.Existence of positive solutions for boundary value problem of third-order differential equations of withp-Laplacian[J].Journal of Hebei University of Science and Technology,2014,35(6):524-528.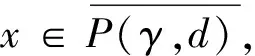

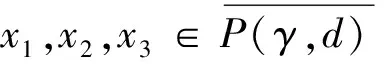
3 相关引理
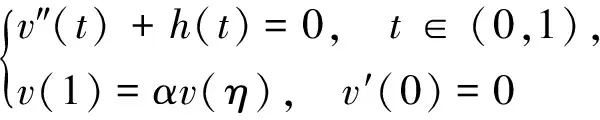
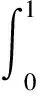
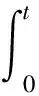
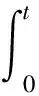
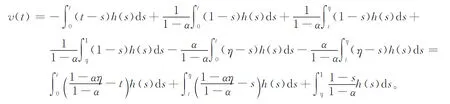
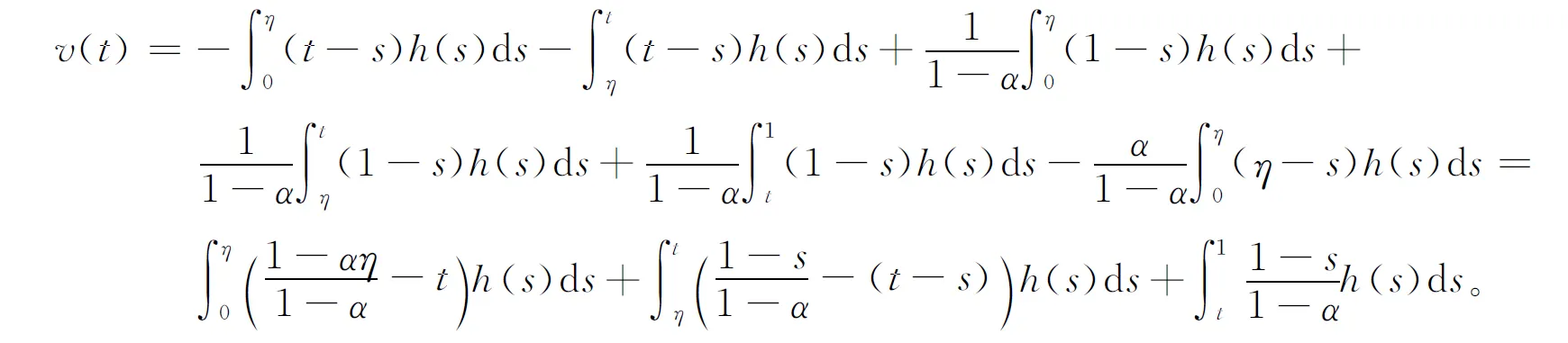
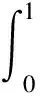
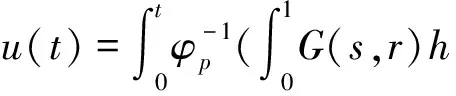
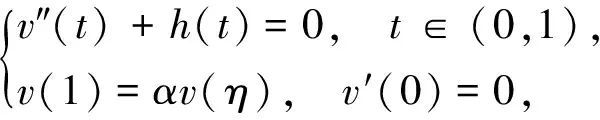
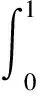
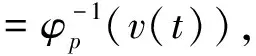
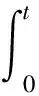
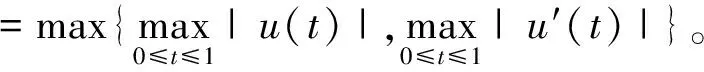
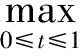
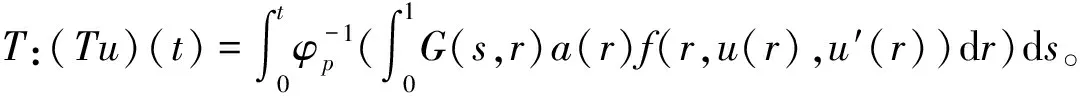
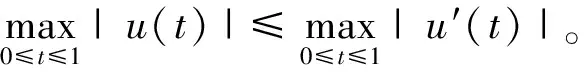
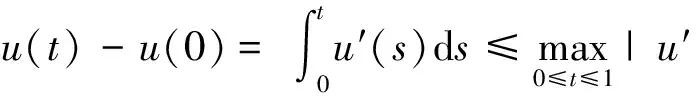
4 三个正解的存在性