基于柱Kadomtsev-Petviashvili模型的海洋内孤立波非线性相互作用传播特征仿真模拟研究
2014-08-28王春梅李玲玲
李 娟,刘 苗,王春梅,李玲玲,董 文
(1.遥感科学国家重点实验室,中国科学院遥感与数字地球研究所,北京 100101;2.国家航天局航天遥感论证中心, 北京 100101)
基于柱Kadomtsev-Petviashvili模型的海洋内孤立波非线性相互作用传播特征仿真模拟研究
李 娟1,2,刘 苗1,2,王春梅1,2,李玲玲1,2,董 文1,2
(1.遥感科学国家重点实验室,中国科学院遥感与数字地球研究所,北京 100101;2.国家航天局航天遥感论证中心, 北京 100101)
在考虑到海洋内波的二维效应时,含有横向微扰的二维模型可以较好地模拟海洋内波的传播,因此为更好地描述海洋内波这一复杂非线性现象的传播特性,利用二维柱Kadomtsev-Petviashvili模型研究了海洋内波非线性相互作用的传播特征。首先,利用解析法获得该二维模型的双抛物线型孤子解,同时模拟研究了南海东沙群岛的海洋内波的弹性碰撞及随时间变化的传播特性;其次,基于不同的海域背景参数分析研究了上升型和下降型抛物线海洋内波弹性碰撞引起的海洋表层流速的变化。经比较分析,本文模拟结果与已有的遥感卫星图像较一致,因此可为进一步深入研究海洋内波的传播特性、动力学机制解及内波参数反演等提供一定的借鉴。
双抛物线型海洋内孤立波;柱Kadomtsev-Petviashvili模型;解析解
利用水平一维动力学模型如Korteweg-de Vries(KdV)方程,科学家们已经对世界多个海域的海洋内波的传播特征进行模拟研究,包括安德曼海、苏禄海、巴士海峡、Sulu海、New York湾和中国南海海域、中国台湾东北海域[1-9],通过实测资料分析、实验室实验、数值模拟、遥感图像分析和解析研究等方法,分析了各海域的海洋内波空间分布特征及季节变化、内波的起源与激发、极性转换等现象。另一方面,在考虑海洋内波的二维效应时,为更好地描述海洋内波这一复杂的非线性现象的传播特性,研究人员逐渐利用相应的二维模型对海洋内波的传播进行模拟和海洋动力学参数反演研究。通过众多研究表明利用二维Kadomtsev-Petviashvili(KP)方程可较好地描述海洋内波的传播特征[10-12]。
1 柱KP模型及孤子解
一般地,描述分层水体结构中海洋内波的传播特征二维柱KP模型可表示为
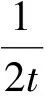
(1)
其中:α=3c0(h1-h2)/(2h2/h2)为非线性系数;β=cuh2/h2/6为频散系数;c0=[gΔρ/ρ0h1h2/(h1+h2)]1/2为线性波速;g是重力加速度;ρ0是海水的平均密度;Δρ是上下分层的密度差。
由式(1)可知,频散系数β>0,故非线性系数α的正负将直接影响海洋内波的波形。在深水域h1


(2)
Zi=λi+2kiTanh[kiξi],


2 海洋内波仿真模型
海洋内波的SAR成像物理机制主要包括[14-17]:海洋内波的传播引起海洋内部流场及表层流速的变化,形成海面辐聚和辐散;变化的表层流场对海洋表面微尺度波的调制作用改变了海洋表面粗糙度;表面微尺度波对SAR雷达波的调制作用通过上述3个过程的综合调制可获得包含丰富海洋内波信息的微波后向散射图像。在密度稳定层化的海洋中,式(1)的上升型海洋内波所引起的海洋表面波的水平流速为
U(i,j)=∓c0ui/hj,
(3)


(4)


(5)
即为进行海洋内波SAR成像模拟的公式。
3 抛物线型海洋内波仿真模拟
据大量的现场观测与遥感数据证实,在中国南海海域存在丰富海洋内波,且该海域的内波存在较明显的时空特征,如文献[14]所示,在南海北部主要有3个区域存在海洋内波现象,包括吕宋海峡、东沙群岛和海南东北部,传播方向以西向为主,每年的4月-9月为海洋内波出现的高峰期,1月-3月和11月-12月为低峰期。图1为1998年4月28日在中国南海海域观测到的海洋内波现象[18],由图1可看出,在海洋内波经过东沙群岛时,其被分成2列,分别从岛的两侧通过,而在通过该岛后,当两者相遇时却发生了非线性相互作用[17]。根据该区域的条件密度氏和浮力频率的分布图水深图及海底地形变化(见图1 b)-图1 d)),平均海水深度可设为h=472 m,上层混合层深h1=60 m,底层深h2=412 m,海洋上下分层密度差Δρ/ρ=0.003 6,在海岸附近,最终的底层深为h2=40 m。

图1 中国南海海域观测到的海洋内波现象及海洋背景参数Fig.1 Internal waves in the Dongsha Islands of South China Sea and ocean background parameters
在较深的海域,图1 d)中A1处的海域深度h1=60 m和h2=412 m具有下降型海洋内波,其在SAR图像上为明暗相间条纹特征。图2为下降型双海洋内波在某一时刻的弹性碰撞过程,与图1 a)相比,可以发现两者具有较好的一致性,2个双抛物线型海洋内波在弹性碰撞时除有微小相位移动外在交换角色后仍能保持原有的特性不变。图3为下降型抛物线海洋内波非线性相互作用引起的海洋表层流速的变化特征(暗亮相间的条纹),与在SAR图像上的特征(亮暗相间条纹)相反,图3 c)和图3 d)为海洋内波弹性碰撞引起的海洋表层流速变化分别在y=0和y=10时的信号特征。

图2 抛物线型下降型海洋内波非线性相互作用过程(λ1=6.05,λ2=-11.05和δ=1)Fig.2 Nonlinear interaction of depression parabola internal wave with λ1=6.05,λ2=-11.05 and δ=1

图3 下降型海洋内波非线性相互作用引起的海洋表层流速的变化特征Fig.3 Signature characteristic of horizontal velocity of the ocean surface current resulted from the depression parabola internal wave

图4 抛物线型下降型海洋内波在t=0.05时非线性相互作用特征及引起的海洋表层流速的变化特征Fig.4 Nonlinear interaction of depression parabola internal wave at t=0.05 and signature characteristic of horizontal velocity of the ocean surface current resulted from the internal wave
随着时间的推移,抛物线型海洋内波的弯曲程度也在不断发生变化,如图4所示。
在较浅的海域,如图1 d)中A2处的海域水深约300 m,混合层深h1=160 m,底层深度h2=h-h1=140 m,故存在上升型海洋内波,其在SAR图像上为暗亮相间条纹特征。图5为双抛物线上升型海洋内波弹性碰撞在某一时刻的传播特征及在y=-5时截面特征。图6为上升型抛物线海洋内波弹性碰撞引起的海洋表层流速的变化特征(明暗相间的条纹),与在SAR图像上的特征相反,图6 b)和图6 c)为上升型双抛物线海洋内波弹性碰撞引起的海洋表层流速变化分别在y=-5和y=21时的信号特征。

图5 抛物线型上升型海洋内波非线性相互作用过程(λ1=8.05,λ2=-15.05和δ=1)Fig.5 Nonlinear interaction of elevation parabola internal wave with λ1=8.05,λ2=-15.05 and δ=1

图6 双抛物线上升型海洋内波引起的海洋表层流速的变化特征Fig.6 Signature characteristic of horizontal velocity of the ocean surface current resulted from the elevation parabola internal wave
4 结 论
本文主要是利用二维柱KP模型模拟了南海东沙群岛的双抛物线型海洋内波的传播特征,同时分析了上升型和下降型抛物线海洋内波非线性相互作用所引起的海洋表层流速的变化。由于缺乏有效历史观测数据和海洋环境参数,故在本文中只是初步的定性分析讨论了双抛物线型海洋内波弹性碰撞的传播特征,而有关的基于二维柱KP模型的海洋内波振幅、传播速度等动力学参数的反演还需要在下一步工作中进行深入研究,只希望本文的研究可为海洋内波进一步的研究提供一定的参考。
/
[1] LIU A K, APEL J R, HOLBROOK J R. Nonlinear internal wave evolution in the Sulu Sea [J]. Journal of Physical Oceanography, 1985, 15: 1613-1624.
[2] LIU A K. Analysis of nonlinear internal waves in the New York Bight[J].Journal of Geophysical Research, 1988, 93: 12317-12329.
[3] LIU A K, CHANG Y S, HSU M K, et al. Evolution of nonlinear internal waves in China Seas [J]. Journal of Geophysical Research, 1998, 103: 7995-8008.
[4] ZHAO Z X, KLEMAS V, ZHENG Q A, et al. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea [J]. Geophysical Research Letters, 2004, 31: 1-4.
[5] CAI S Q, XIE J S, XU J X, et al. Monthly variation of some parameters about internal solitary waves in the South China Sea [J]. Deep-Sea Research I, 2014, 84:73-85.
[6] 吕海滨, 申 辉, 何宜军. 背景流和混合层深度对内波表面信号的影响 [J]. 海洋科学, 2013, 37(9):20-23. LYU Haibin, SHEN Hui, HE Yijun. The effects of background current and pycnocline depth on surface signals of internal waves [J]. Marine Sciences, 2013, 37(9):20-23.
[7] 刘永军, 宋金宝, 黄小峰. 非传统近似下海洋内波的一类WKB近似解 [J]. 海洋科学, 2011, 35(1):82-87. LIU Yongjun,SONG Jinbao,HUANG Xiaofeng. A type of WKB solutions for internal waves under the non-traditional approximation [J]. Marine Sciences, 2011, 35(1):82-87.
[8] GUO C, CHEN X. A review of internal solitary wave dynamics in the northern South China Sea [J]. Progress in Oceanography, 2014, 121: 7-23.
[9] KUMAR S, SINGH K, GUPTA R K. Dynamics of internal waves in a stratified ocean modeled by the extended Gardner equation with time-dependent coefficients [J]. Ocean Engineering, 2013, 70:81-87.
[10] 李 群, 孙 丽, 徐肇廷. 内孤立波波-波相互作用的数值模拟 [J].中国海洋大学学报, 2007, 37(6):868-872. LI Qun, SUN Li, XU Zhaoting. Modeling the wave-wave interaction between internal solitary waves[J]. Periodical of Ocean University of China, 2007, 37(6):868-872.
[11] MENG J M, ZHANG Z L, ZHAO J S. The simulation of the SAR image of internal solitary waves in Alboran Sea [J]. Journal of Hydrodynamics Series B, 2001(3):88-92.
[12] PIERINI S. A model for the alboran sea internal solitary waves [J]. Journal of Physical Oceanography,1989,19:722-755.
[13] LI J, ZHANG H Q, XU T, et al. Symbolic computation on the multi-soliton-like solutions of the cylindrical Kadomtsev-Petviashvili equation from dusty plasmas [J]. Journal of Physics Mathematical and Theoretical,2007, 40:7643-7657.
[14] 蔡树群, 甘子钧, 龙小敏. 南海北部孤立子内波的一些特征和演变 [J]. 科学通报,2001,46: 1245-1250. CAI Shuqun, GAN Zijun, LONG Xiaomin.Some characteristics and evolution of the internal soliton in the northern South China Sea [J].Chinese Science Bulletin, 2001, 46: 1245-1250.
[15] 李海艳.利用合成孔径雷达研究海洋内波 [D].青岛:中国海洋大学, 2004. LI Haiyan.Studying Ocean Internal Waves with SAR [D].Qingdao:Ocean University of China, 2004.
[16] 杨劲松.合成孔径雷达海面风场、海浪和内波遥感技术 [M]. 北京:海洋出版社,2005. YANG Jinsong. Ocean Surface Wind Wave and Internal Wave Remote Sensing Technology Based on Synthetic Aperture Radar [M]. Beijing: Ocean Press, 2005.
[17] 申 辉.海洋内波的遥感与数值模拟研究[D].青岛:中国科学院海洋研究所, 2005. SHEN Hui. Remote Sensing and Numerical Modeling of Oceanic Internal Waves [D]. Qingdao:Institute of Oceanology of Chinese Academy of Sciences, 2005.
[18] HSU M K, LIU A K. Nonlinear internal waves in the South China Sea [J]. Canadian Journal of Remote Sensing, 2000, 26: 72-81.
Simulation investigations on nonlinear interaction of ocean internal waves via the cylindrical Kadomtsev-Petviashvili model
LI Juan1,2, LIU Miao1,2, WANG Chunmei1,2, LI Lingling1,2, DONG Wen1,2
(1. State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China; 2. Demonstration Center for Spaceborne Remote Sensing National Space Administration, Beijing 100101, China)
In view of the two-dimensional effects of ocean internal waves, the two-dimensional model containing transverse perturbation can well simulate the propagation character of ocean internal waves. In this paper, the cylindrical Kadomtsev-Petviashvili model has been used to depict the propagation character of nonlinear interaction of ocean internal waves. By making use of the analytical method, the biparabolic solitary solution of this 2-dimensional equation is derived. The elastic collision and the time-varying propogation character of ocean internal waves of Dongsha Islands of the South China Sea are studied and simulated .The simulation results are consistent with that of remote sensing satellites images, and then can be provided as a reference for further research on nonlinear interaction and polar transformation of ocean internal waves.
biparabolic ocean internal wave; cylindrical Kadomtsev-Petviashvili model; analytical solution
2014-06-17;
2014-08-28;责任编辑:张 军
国家自然科学基金(11101421); 中国科学院遥感应用研究所知识创新工场青年人才领域前沿项目(Y1S01500CX)
李 娟(1978-), 女, 山东聊城人, 副研究员, 博士,主要从事海洋内波传播特性方面的研究。
E-mail:lijuan@radi.ac.cn
1008-1542(2014)06-0512-06
10.7535/hbkd.2014yx06003
P731.24
A
李 娟,刘 苗,王春梅,等. 基于柱Kadomtsev-Petviashvili模型的海洋内孤立波非线性相互作用传播特征仿真模拟研究[J].河北科技大学学报,2014,35(6):512-517.
LI Juan,LIU Miao, WANG Chunmei,et al. Simulation investigation on the nonlinear interaction of internal waves via the cylindrical Kadomtsev-Petviashvili model[J]. Journal of Hebei University of Science and Technology,2014,35(6):512-517.
