一种非均匀动态子带划分OFDM自适应调制算法

李 莉，张锡岭，李飞凡，邹传超

（中国石油大学（华东）计算机与通信工程学院，山东青岛 266580）

OFDM技术中由于各个子载波是正交的，其频谱可以相互重叠，因此该技术频谱利用率高、具备高速信息传输的能力，而且是对抗频率选择性衰落的重要手段之一，被广泛认为是高速数字传输的首选调制技术，是宽带无线通信网络的核心物理层技术。自适应调制技术能根据当前子信道状态及时改变每个子载波的调制模式、发射功率及编码类型，能最大限度地利用系统的容量和频谱资源，提高功率效率，成为OFDM系统研究的核心问题之一［1-3］。

经典自适应调制算法主要有注水法、Chow算法、Fischer算法等，在以上算法基础上，又提出了多种改进算法［4-6］。但上述算法均采用子信道为单位进行比特和功率分配，为了有效减小系统中自适应调制信息的信令开销，降低算法复杂度，目前，已有文献对基于子带划分的自适应调制算法进行了研究［7-9］。该类算法将子载波划分为子带，对同一子带中的子载波采用相同的比特和功率分配，但为了保证子带划分后的系统性能，对子带划分基本要求是子带宽度不大于信道的相干带宽。其中基于固定门限的简单分块加载算法（simple block loading algorithm，SBLA）是复杂度较低的子带划分算法之一［10］，该算法中子带数不变，通过与预先设定的信噪比门限比较一次即能完成比特预分配，因此算法复杂度低、实时性强；而动态子带划分自适应算法能根据子信道信噪比的变化来调整子带划分，从而使算法性能尽可能接近不采用子带划分时的系统性能［11-12］。由此，本文结合SBLA算法与动态子带划分自适应算法的优势，提出一种非均匀动态子带划分OFDM自适应调制算法（an non-uniform dynamic sub-band division adaptive modulation algorithm of OFDM，简称NUDS算法）。NUDS算法能根据信道的频响关系无需迭代完成动态子带划分，采用SBLA算法实现比特预分配，能极大减少算法迭代次数；在比特调整中充分利用信噪比最大的子带，能在降低算法复杂度，减小系统信令开销的情况下，充分保证系统性能，仿真结果证明了该结论。

1 OFDM自适应调制系统模型

单用户自适应调制OFDM系统框图如图1所示［13］。首先在系统接收端，所有子信道的信道频率响应能根据信道估计获得，然后子信道的信道频率响应通过反馈信道传送到发送端；根据子信道的实时信噪比，通过采用的自适应调制算法，一般可在系统发送端来实现子载波的比特和功率的动态资源分配，然后将形成的OFDM符号发送到信道，同时自适应调制信令信息被传送到接收端。系统接收端的解调模块需要根据子信道频率响应和自适应调制信息来完成信号解调，实现发送数据的恢复。为了保证接收机的正确解调，子载波的信道频率响应和自适应调制信息传输必须高效可靠。

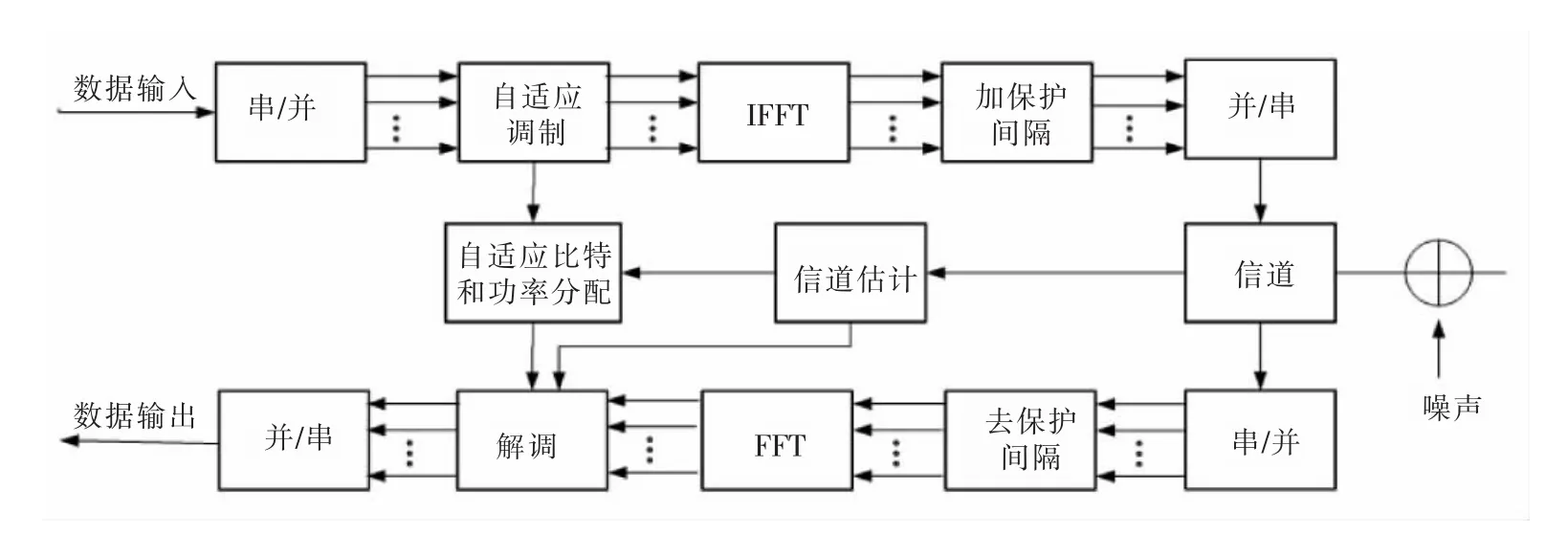
图1 单用户自适应调制OFDM系统框图Fig.1 Block of single user adaptive modulation OFDM system

2 NUDS算法

NUDS算法的优化目标是基于RA优化准则的，即在满足系统总发送功率和最大误码率限制的条件下，保证系统获得最大的传输速率。本算法的第一步是根据子载波的实时信道频率响应来实现动态子带划分算法。

2.1 动态子带划分算法

在本文中，假定将频率选择性衰落信道划分为K个平坦衰落的窄带子信道，定义子载波i的接收端信噪比为

式中H（i）是子信道i的信道频率响应，i=1，2，…，K，σ2为子信道噪声功率。

由文献［14］可知，根据信道的频响关系，K个子载波可划分为N个子带：

由式（3）求解各子带中包含的子载波：

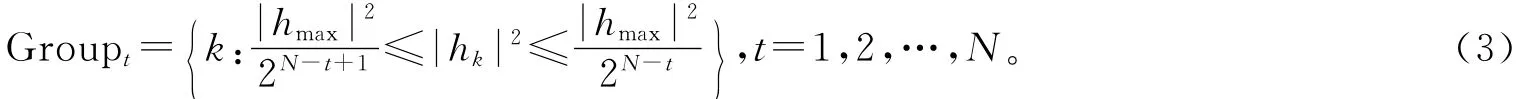
第t个子带包含的子载波数称为该子带的子带宽度b t，t=1，2，…，N，第t个子带中的子载波可表示为t（i），i=1，2，…，bt。显然，通过式（2）和式（3）由信道实时频率响应，无需迭代即能实现动态的子带划分，因此能极大地降低子带划分算法的计算复杂度，提高算法实时性。

文献［15］采用随机选取（CSG-RS：Random select）方案，将第t个子带的等效信噪比（t）定义为

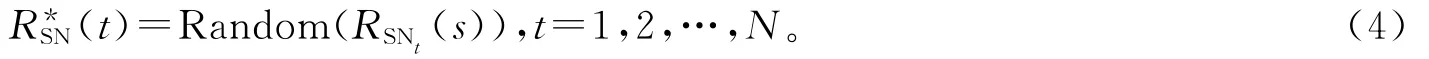
其中，RSNt（s）表示第t个子带中第s个子载波的信噪比。文献［15］表明，“随机选取方案”比常用的“算术平均值方案”、“最小增益（Min）方案”具有较低的计算复杂度，且能获得较好的系统误码率性能。SN（i）是子带划分后第i个子载波的等效信噪比，即当第i个子载波属于第t个子带时，

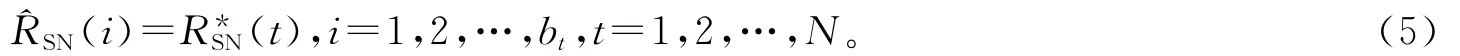
2.2 算法流程

通过2.1中子带划分算法完成子带划分后，各子带中的子载波均按照信噪比从小到大顺序排列。然后，根据SBLA算法为子带中的子载波分配相同的比特，实现比特预分配；最后根据以下算法流程中的比特调整方法完成比特调整。比特调整的基本原则是充分利用信噪比最大的子带，即完成子带划分后最后一个子带组。算法流程如下。

1）初始化。设OFDM符号的子载波总数为K，每个子载波平均需要传输的比特数为m，一个OFDM符号包含的目标比特数Rtarget=m K。

2）由 OFDM 系统仿真BER曲线确定各调制方案的信噪比门限RSNstd（j），其中j=0，1，2，3，4，表示不同调制级别。

3）由子载波i的信道频率响应H（i），根据式（2）和式（3）估算OFDM符号的子带数N和子带宽度b。

式中：TS为山东节假日期间客流量的增加值，S为节假日的时长，相关系数R=0.973 6，方程拟合度较高，即节假日每增加(或减少)一天，客流量将增加(或减少)255.7人次。

6）若Rtotal＞Rtarget，计算max＿allo（N）=R（N）＊b N，即预分配比特数最多的子带为第N个子带，比较max＿allo（N）与Rtarget大小。

7）若max＿allo（N）=Rtargtet为第N个子带分配R（N）个比特，其余子带分配比特数均为0，则Rtotal=Rtarget，比特调整结束，转至11）。

8）若max＿allo（N）＜Rtarget，则重复更新max＿allo（N-i）=max＿allo（N）＋R（N-i）＊b（N-i），i=1，2，…，N-1，直至max＿allo（N-i）＞Rtarget，记录当前子带号p=N-i。计算第p个子带中多余的比特数目surplus＿bit=max＿allo（t）-Rtarget和比率因子rate=surplus＿bit／bp，然后执行 ⅰ），ⅱ），ⅲ）。

ⅰ）若rate＞1，调整R（p）=R（p）-fix（rate），max＿allo（p）=max＿allo（p）-fix（rate）＊bp，rate=rate-fix（rate），surplus＿bit=max＿allo（p）-Rtarget；若rate=0，比特调整结束，转至11）；否则执行 ⅱ）。

ⅱ）若rate＜1，将当前子带p划分为2个新子带p和p＋1，这2个子带的子载波分别由原子带p中的后bp-surplus＿bit和前surplus＿bit个子载波构成，调整R（p＋1）=R（p）-1，即将第p＋1个子带的调制级别减1。则Rtotal=Rtarget，比特调整结束，转至11）。

ⅲ）若rate=1，调整R（p）=R（p）-1，则Rtotal=Rtarget，比特调整结束，转至11）。

9）若 max＿allo（N）＞Rtarget。记录当前子带号p=N。计算surplus＿bit=max＿allo（p）-Rtarget，rate=surplus＿bit／bp，然后执行 ⅰ），ⅱ），ⅲ）。

11）发射功率Ptarget在可用子载波上均匀分配。

3 仿真与分析

3.1 系统参数

本文中OFDM系统仿真参数设置见表1。系统可选择调制方式为0（即子信道关闭），BPSK，4QAM，8QAM，16QAM，对应的比特数分别为0，1，2，3，4。OFDM 符号的目标比特数为128 bit，平均每个子信道传输2 bit，即不采用自适应调制时采用4QAM调制。仿真采用多径信道，信道自相关时间为625μs，功率时延谱见表1，噪声模型为高斯白噪声。图2中显示了采用Matlab仿真所获得在以上系统参数设置下，分别采用不同固定调制方式情况下系统的误码率曲线图。在图2中，各条误码率曲线在系统目标误码率（BER=10-3）时的信噪比取值，即是当前系统下各种调制方式的信噪比门限，具体见表2。

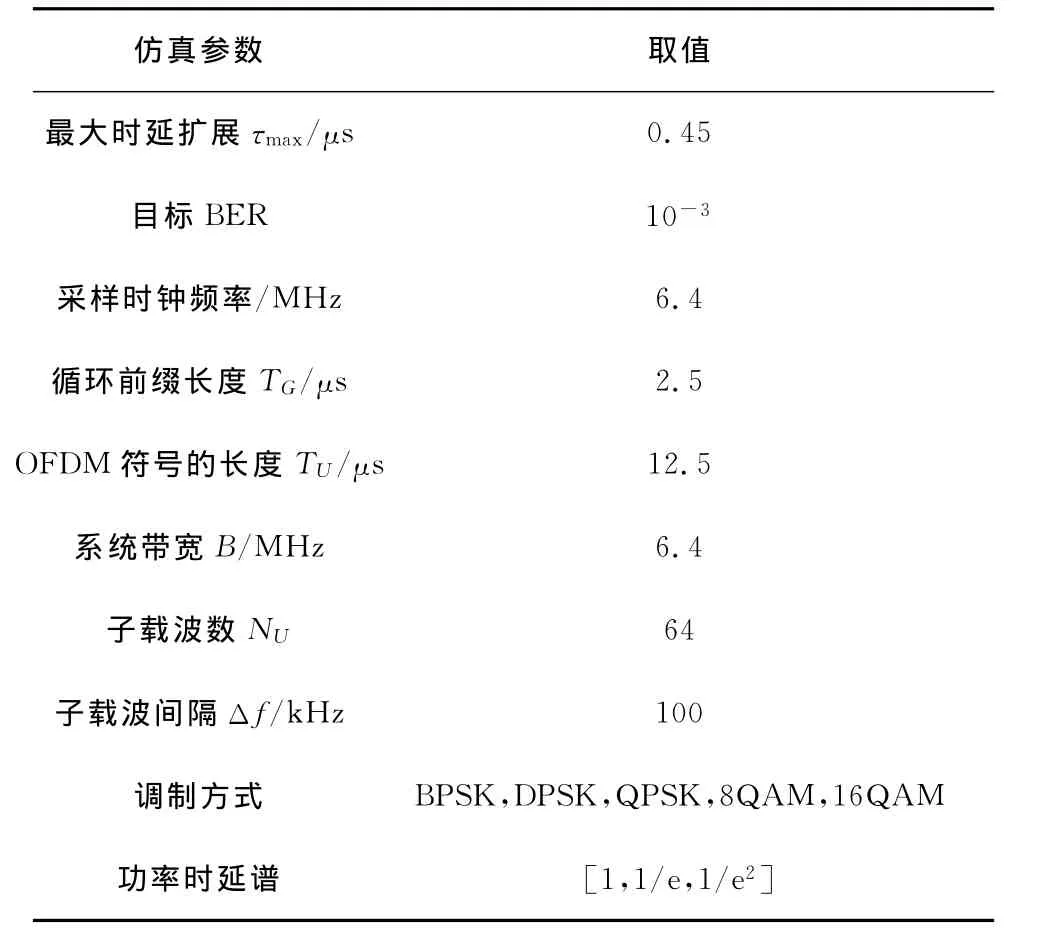
表1 OFDM系统仿真参数Tab.1 LPLC-OFDM system simulation parameters

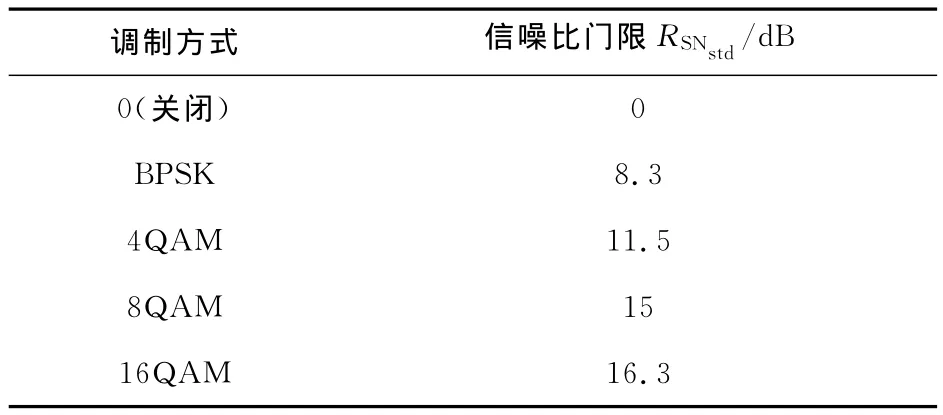
表2 信噪比门限Tab.2 SNR threshold

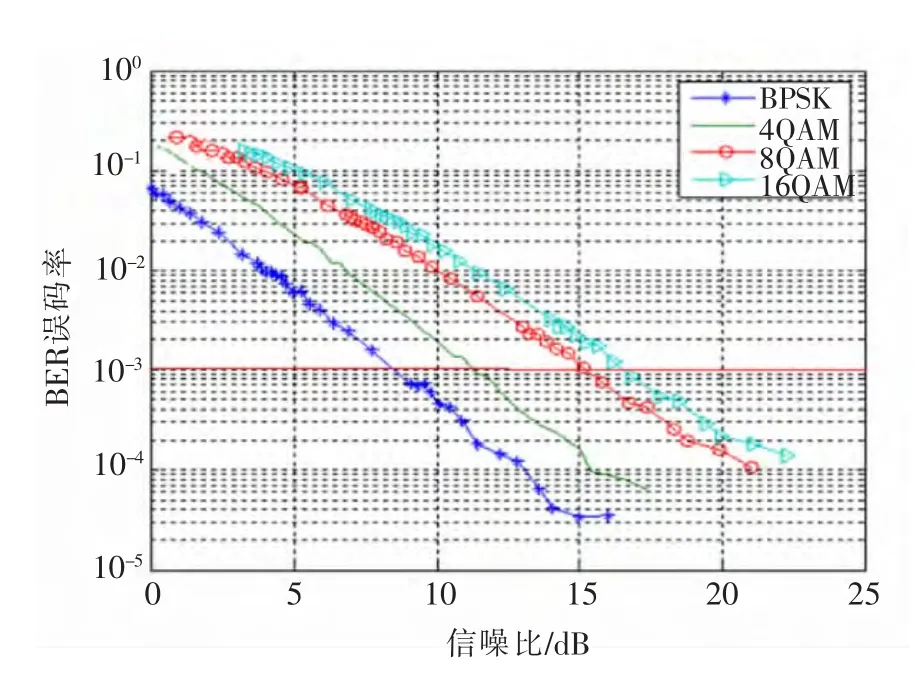
图2 不同调制方式下OFDM系统误码率曲线Fig.2 BER on different modulation modes in OFDM system

3.2 算法复杂度分析

表3比较了Chow算法、NUDS算法、SBLA算法运算中所需要的比较次数、乘法次数和对数次数。显然NUDS算法、SBLA算法复杂度都主要由子载波数目K、子带数N及目标比特数Rtarget决定，当K和Rtarget固定不变时，算法复杂度会随着子带数N的增加而增大。SBLA算法是这3种算法中复杂度最低的，由于NUDS算法和SBLA算法都是以子带为单位进行比特调整的，所以其比特调整的迭代次数count＊要远远小于Chow算法的以子信道为单位进行比特调整所需的比特调整迭代次数count；并且由于NUDS算法采用的非均匀动态子带划分算法，无需迭代就能实现子带的划分，所以NUDS算法相比SBLA算法复杂度提高的不多；显然NUDS算法和SBLA算法都比Chow算法的复杂度低。

表3 算法复杂度比较Tab.3 Complexity comparison of different algorithms

3.3 仿真分析

在3.1所述的OFDM系统平台下完成NUDS算法的仿真与分析。一次仿真中，共发送2 500个OFDM帧，其中一个OFDM帧包含20个OFDM符号。本文假设信道状态在一个OFDM帧内不变，系统符号同步、采样时钟同步及信道估计均是理想的，且不考虑信道状态信息和调制方案信息的传输误差。

图3所示的是2个不同时刻的信道状态及采用NUDS算法完成的子载波比特分配结果。显然，NUDS算法能跟踪信道状况，动态地为子信道选择合适的调制方式：信道性能好的子信道分配比特数较多；信道性能差的子信道分配比特数较少甚至被关闭。显然，比特分配的仿真结果符合算法的设计思路。

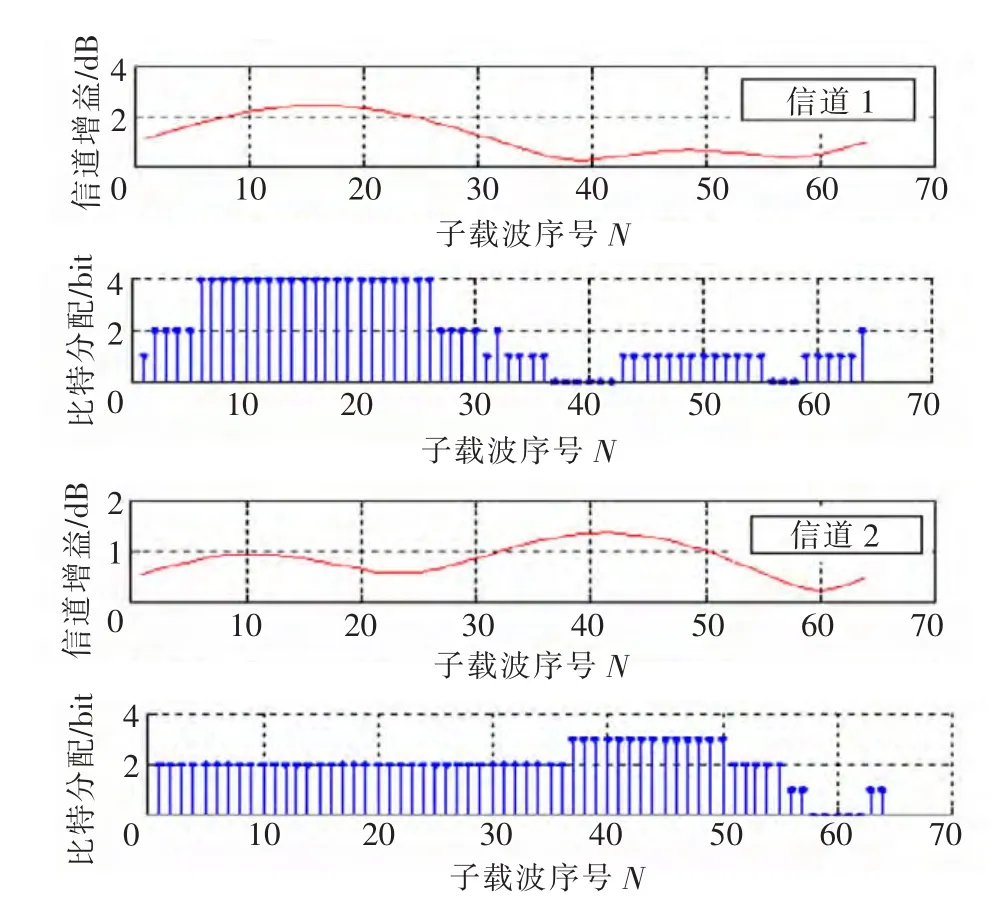
图3 信道增益与NUDS算法比特分配结果Fig.3 Channel gain and bit allocation result of NUDS algorithm

图4给出了分别采用NUDS算法、Chow算法、4QAM固定调制方法时系统误码率对比图。由图4可知，信噪比相同时，采用NUDS算法相比采用4QAM调制，系统误码性能有了明显改善，抗噪声性能有了一定提高。例如，系统达到目标误码率BER=10-3时，NUDS算法相比较4QAM调制而言能获得的信噪比增益约为2.6 d B；NUDS算法与Chow算法性能相近，表明NUDS算法能获得接近Chow算法的最优比特分配，但由3.1节分析可知NUDS算法迭代次数较少、复杂度较低。

图5给出了采用NUDS算法、SBLA算法时系统误码率对比图。在BER=10-3时，NUDS算法相比SBLA算法（子带宽度为8）能获得约2 dB的信噪比增益。但是，固定门限自适应算法的系统性能与子带宽度b关系密切，子带宽度b越小，子载波信噪比的均方误差MSE就越小，系统的误码率下降，但传递调制方式及信道消息的信令开销会增大，算法复杂度也越大；因此，由仿真结果的分析可知NUDS算法能在保证系统误码性能的前提下，减小系统信令开销，降低算法的复杂度。

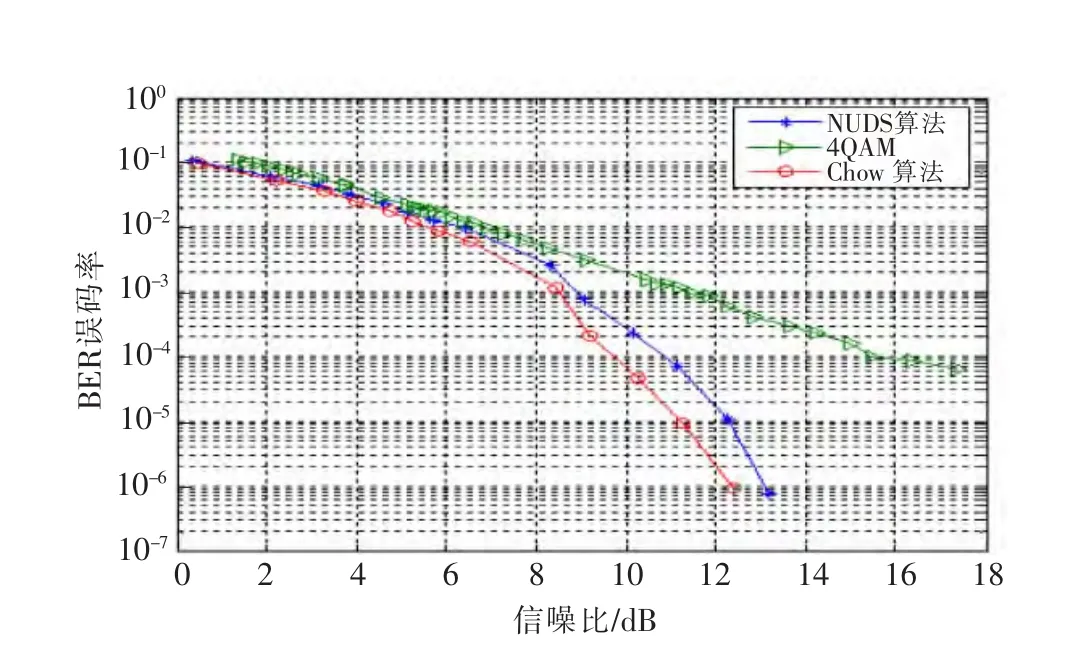
图4 不同算法的OFDM系统误码率曲线Fig.4 BER on different algorithms in OFDM system

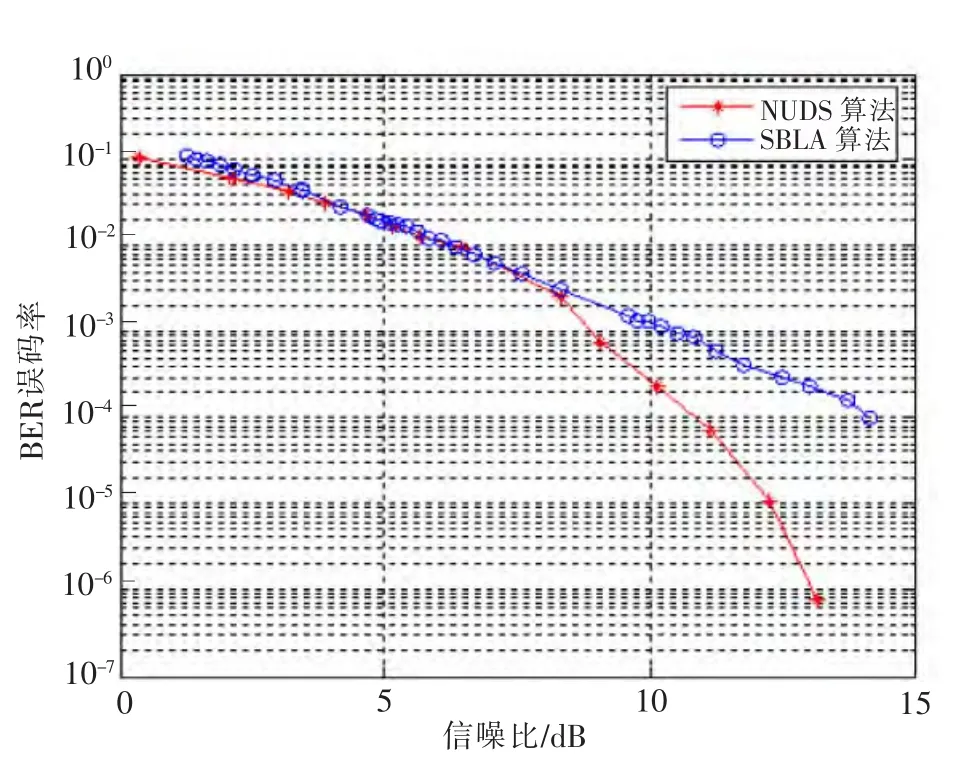
图5 NUDS算法与SBLA算法的性能对比Fig.5 Performance comparison of NUDS algorithm and SBLA of the algorithm

4 结 语

本文提出的NUDS算法在采用随机选取方案定义子带等效频率响应的基础上，根据信道的频响关系，无需迭代即实现了动态子带划分，根据基于固定门限的简单分块加载算法（SBLA）无需迭代即实现子载波的比特预分配，并充分利用信噪比最大的子带来完成比特调整。仿真结果表明：该改进算法性能接近Chow算法，极大减小了系统信令开销；能有效降低算法复杂度，减少调制信令信息的传递，且不牺牲系统性能，因此具有一定的优越性和实用价值。但是，本算法未考虑严格的OFDM同步、信道估计的误差对自适应调制算法及系统性能的影响等问题，还有待进一步研究。

／References：

［1］ 戚佳金，陈雪萍，刘晓剩.低压电力线载波通信技术研究进展［J］.电网技术，2010，34（5）：161-172.QI Jiajin，CHEN Xueping，LIU Xiaosheng.Advances of research on low-voltage power line carrier communication technology［J］.Power System Technology，2010，34（5）：161-172.

［2］ 安 宁，李兵兵，黄 敏.自适应OFDM系统子载波调制方式盲识别算法［J］.西北大学学报（自然科学版），2011，41（2）：231-234.AN Ning，LI Bingbing，HUANG Min.Blind subcarrier modulation classification algorithm for adaptive OFDM system［J］.Journal of Northwest University（Natural Science Edition），2011，41（2）：231-234.

［3］ NAGARAJ S.Symbol-level adaptive modulation for coded OFDM on block fading channels［J］.IEEE Transactions on Communications，2009，57（10）：2872-2875.

［4］ 汪晋宽，韩 鹏，许 鹏，等.一种适用于OFDM系统的块状导频自适应方案［J］.东北大学学报（自然科学版），2011，32（5）：642-645.WANG Jinkuan，HAN Peng，XU Peng，et al.An adaptive block pilot scheme for OFDM systems［J］.Journal of Northeastern University（Natural Science），2011，32（5）：642-645.

［5］ HUANG Xiaozhou，WU Xsiaochun，WU Yiyan.Novel pilot-free adaptive modulation for wireless OFDM systems［J］.IEEE Transactions on Vehicular Technology，2008，57（6）：3863-3867.

［6］ 唐朝伟，赵丽娟，邵艳清，等.MIMO-OFDM系统自适应分步功率分配算法［J］.华中科技大学学报（自然科学版），2010，38（4）：18-21.TANG Chaowei，ZHAO Lijuan，SHAO Yanqing，et al.Adaptive step-by-step power allocation algorithm for MIMO-OFDM systems［J］.Journal of Huazhong University of Science and Technology（Nature Science Edition），2010，38（4）：18-21.

［7］ LEE S M，PARK Y S.Fast bit and power allocation algorithm for OFDM systems［A］.IEEE VTC［C］.［S.l.］：［s.n.］，2004：503-506.

［8］ LEI Ming，ZHANG Ping.Subband bit and power loading for adaptive OFDM［A］.IEEE VTC［C］.［S.l.］：［s.n.］，2003：1482-1486.

［9］ KOBAYASHI H，TENG Y，NAGAOSA T，et al.Proposal of grouping adaptive modulation method for burst mode OFDM transmission system ［J］.IEICE Transactions on Communications，2003，86（1）：257-265.

［10］ GRUNHEID R，BOLINTH E，ROHLING H.A blockwise loading algorithm for the adaptive modulation technique in OFDM systems［A］.IEEE VTC［C］.［S.l.］：［s.n.］，2001：948-951.

［11］ 蔡丽萍，刘 盈，薛先俊.一种吞吐量最大化的电力线OFDM分子带自适应算法［J］.计算机应用与软件，2012，29（6）：260-263.CAI Liping，LIU Ying，XUE Xianjun.An adaptive algorithm with throughput maximization based on OFDM sub-bands division for power line［J］.Computer Applications and Software，2012，29（6）：260-263.

［12］ 刘 盈，代鹏飞，蔡丽萍，等.基于子带动态划分的电力线OFDM自适应算法研究［J］.计算机工程与设计，2012，33（5）：1720-1724.LIU Ying，DAI Pengfei，CAI Liping，et a1.Analysis of adaptive OFDM algorithm based on dynamical sub-bands division for power line carrier censor network［J］.Computer Engineering and Design，2012，33（5）：1720-1724.

［13］ BANSAL G，HASAN Z，HOSSAIN M J.Subcarrier and power adaptation for multiuser OFDM based cognitive radio systems［A］.2010 National Conference on Communications［C］.Chennai：IEEE，2010：1-5.

［14］ NADER-ESFAHANI S，AFRASIABI M.Simple bit loading algorithm for OFDM-based systems［J］.IET Communications，2007，1（3）：312-316.

［15］ 张世超，季仲梅，崔维嘉.MIMO-OFDM系统中一种高效的分子带自适应比特功率分配算法［J］.电路与系统学报，2012，17（4）：103-110.ZHANG Shichao，JI Zhongmei，CUI Weijia.An efficient subband adaptive bit and power allocation algorithm for MIMO-OFDM systems［J］.Journal of Circuits and Systems，2012，17（4）：103-110.