基于序列线性规划的空间钢框架优化

朱杰江 孙宇鸣

1 引 言

钢结构具有自重轻、施工简便、易于环保等优点，随着我国钢产量不断提高，钢结构被越来越广泛地应用。目前制约钢结构发展的因素主要是钢结构直接造价高于钢筋混凝土结构[1]，故对钢结构进行优化设计有现实经济意义。

对于钢桁架结构，目前已有较成熟的基于数学规划法及粒子群算法、遗传算法等启发式算法的优化研究[2-4]，对于钢框架结构优化的研究则相对较少。

宫海，李国强[5]采用一种由拉格朗日乘子法与虚功原理组合而得的位移准则法，采用局部(构件强度稳定性)与整体(整体位移)优化算法相结合方式，对空间多层、高层钢框架进行截面尺寸的优化。

Stojan等[6]基于非线性规划针对单层门式刚架的截面以及布局优化进行研究。Kaveh等[7,8]将蚁群算法运用到基于性能的平面钢框架优化设计中。

黄冀卓，王湛[9]以一种两阶段优化策略实现了支撑的连续体拓扑优化，第一阶段控制构件，不控制整体位移，第二阶段针对钢框架-支撑结构中支撑位置、布局，以平面结构的整个立面为连续设计区域，进行支撑体系的拓扑优化。

目前纯钢框架结构的优化研究，对于层间相对位移约束的处理仍较为被动，通常需要与构件的强度及稳定性进行分级优化。考虑到钢框架结构侧向刚度低往往导致截面进一步加大，进而可能影响优化效果，本文基于序列线性规划和对偶仿射尺度法，将结构层间位移约束置于与构件应力约束同等地位，优化时对层间位移及柱顶位移进行主动控制。并且，考虑到工程实际运用，直接对空间多层钢框架结构进行整体优化。

2 数学规划法原理

2.1 序列线性规划

序列线性规划(Sequence Linear Programming,SLP)是非线性规划中一种成熟的解法，它将非线性规划问题转化成线性规划问题，然后用单纯形法求解该线性规划。对于目标函数及约束条件，都可以使用泰勒展开取其线性项来逼近原函数，对于多元函数f(X1,X2, …,Xn)有

(1)

式中，df(k)(X1,X2, …,Xn)为f(X1,X2, …,Xn)在第k次序列线性规划循环时的全微分，表示为

(2)

式中，{dX}为优化变量X1,X2, …,Xn的微元dX1, dX2, …, dXn所组成的列向量。

这样，就完成了目标函数、约束条件的线性化。

2.2 对偶仿射尺度法

对以往的序列线性规划方法加以改进，采用对偶仿射尺度法来替代单纯形法完成线性规划的求解。

对偶仿射尺度法是基于内点法的一种线性规划算法。与单纯形法所不同的是，内点法在可行域的内部搜索最优解，而不是可行域的边界。因此，对于规模较大的线性规划问题，内点法的迭代效率高于单纯形法[10]。

考虑非对称的对偶规划，如式(3)所示。

(3)

求解的基本步骤如下：

(1) 找出初始可行解(y0,z0)满足

ATy0+z0=c,z0>0

(4)

令k=0。

(2) 求搜索方向，令Sk=diag(zk)，并计算

(5)

(5) 若xk≥0,cTxk-bTyk=0，则停止，(yk,zk)为最优解；否则，进行第(6)步。

(6) 计算步长

(6)

(7) 校正解

(7)

令k=k+ 1，返回到第(2)步，不断循环，直至满足停止条件。

3 优化模型

3.1 总则

本文以结构框架用钢的体积最小为目标函数，如式(8)所示。

(8)

式中，Li为第i个杆件的长度;Ai为第i个杆件的面积;n为杆件数。

根据序列线性规划的原理，取得目标函数(8)的全微分，来构建一个线性规划问题，如式(9)所示。

(9)

对于第i个约束条件

N≤gi≤P

(10)

可作以下变换取得线性约束条件

(11)

式中，k表示序列线性规划的循环次数；P为约束的上限；N为约束的下限；gi代表结构的某响应，为优化变量的隐函数，问题归结为取得各结构响应关于优化变量的全微分。

3.2 基于空间梁系有限元法的优化模型

使用不考虑剪切变形的梁单元，对于局部坐标系下单元(图1)，有以下控制方程组，

图1 梁(柱)单元示意图Fig.1 Beam (column) element

式(12a)中，

(13)

(14)

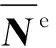
式(12b)为节点平衡方程，其中，

(15)

(16)

(17)

将式(12a)式(12c)代入式(12b)得

(18)

(19)

式(19)即单元在局部坐标系下的单元刚度矩阵。

(20)

坐标转换后整合所有杆件取得结构的控制方程组：

对式(21b)、式(21c)、式(21e)展开得

将式(23)代入式(22)

最终可得

(25)

通过该列向量可对结构任意节点6个自由度的位移施加约束条件。

整理得结构整体优化的有限元模型：

(26)

3.3 约束条件

应力约束考虑构件强度及稳定性，如式(27)—式(29)所示：

(27)

(28)

(29)

式中，γRE为抗震承载力调整系数；γy，γz分别为截面两个主轴塑性发展系数；φy，φz为轴心受压稳定系数，根据《钢结构设计规范》[11](GB 50017—2003)附录C、D确定；φby，φbz为受弯整体稳定系数，根据《规范》[11]附录B确定；f为钢材强度设计值，根据《规范》[11]表3.4.1-1确定。

层间相对位移满足

(30)

式中，Δδj为第j层水平位移；hj为第j层层高；δju为允许层间位移角，风荷载作用下[11]为1/400，地震作用下[12]为1/250。

此外，框架柱顶风荷载作用下允许位移取H/500(H为结构高度)。

3.4 截面设计及优化变量

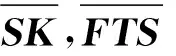
描述截面尺寸可以是单参数，也可以是多参数。对于焊接型钢，可以描述截面的若干参数推导6个物理量关于参数的函数。例如，对于焊接圆管，以内径d及外径D作为优化设计变量；对于焊接H型钢，以翼缘宽度b及截面全高h为优化设计变量，其他参数则假定为b,h的牵连变量，设计截面时即可在一定程度上避免局部稳定超限。这样，截面力学参数可表示为b,h的函数，如截面的惯性矩和截面模量可表示为

(31)

其全微分可表示为

(32)

4 算 例

以两个空间钢框架为优化算例，优化期间直接控制序列线性规划循环次数，而对偶仿射尺度法迭代次数直接取30。构件全部采用以b,h为设计变量的双参数焊接H型钢(式(31)、式(32))，材料采用Q345。

结构重要性系数取1.0，中梁、边梁刚度放大系数分别按《高层民用建筑钢结构技术规程》[13](JGJ 99—98)条文5.1.3取1.5和1.2；场地特征周期取0.9 s，抗震设防烈度为7度，水平地震影响系数最大值取0.08，阻尼比取0.035，周期折减系数取0.7，考虑双向地震作用并采用CQC振型组合方法；地面粗糙度类别为C类，基本风压取0.55 kN/m2，风荷载体型系数取1.3。考虑恒载、活载、风荷载、地震作用的35种荷载效应组合，并采用刚性楼板假定。

4.1 算例一

算例一为一个二层不规则简单框架，如图2所示，底层柱距为6 m，首层层高6 m，2层层高4 m。

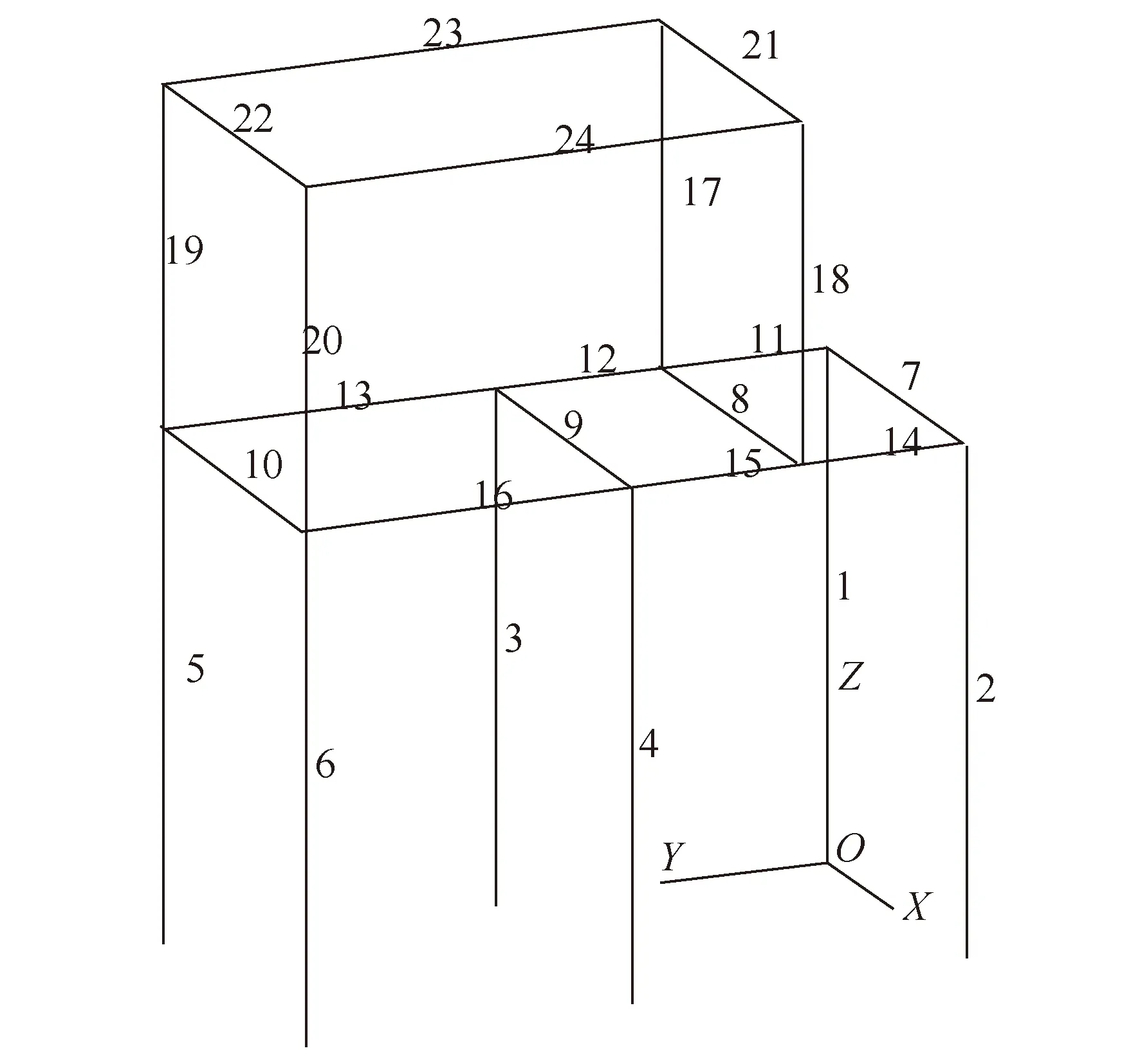
图2 算例一结构示意图Fig.2 The 1st Model

首先，不控制结构整体位移，将应力比约束条件分别设置为0.95，0.65，0.35，进行20次SLP循环，优化曲线如图3所示。

图3显示，虽然迭代在中后期表现出跳跃特点，但优化曲线总体上表现为收敛；并且，应力比约束越小，材料用量越大，证明优化程序是有效的，且与实际相符合。

考察应力比约束取0.95时优化的最终情况，在第17次迭代时结构用钢量达到最低的0.314 m3，杆20达到最大应力比0.938，与应力比约束条件值相近。此时的结构层间位移角列于表1，结构优化后的宏观效果见图4。

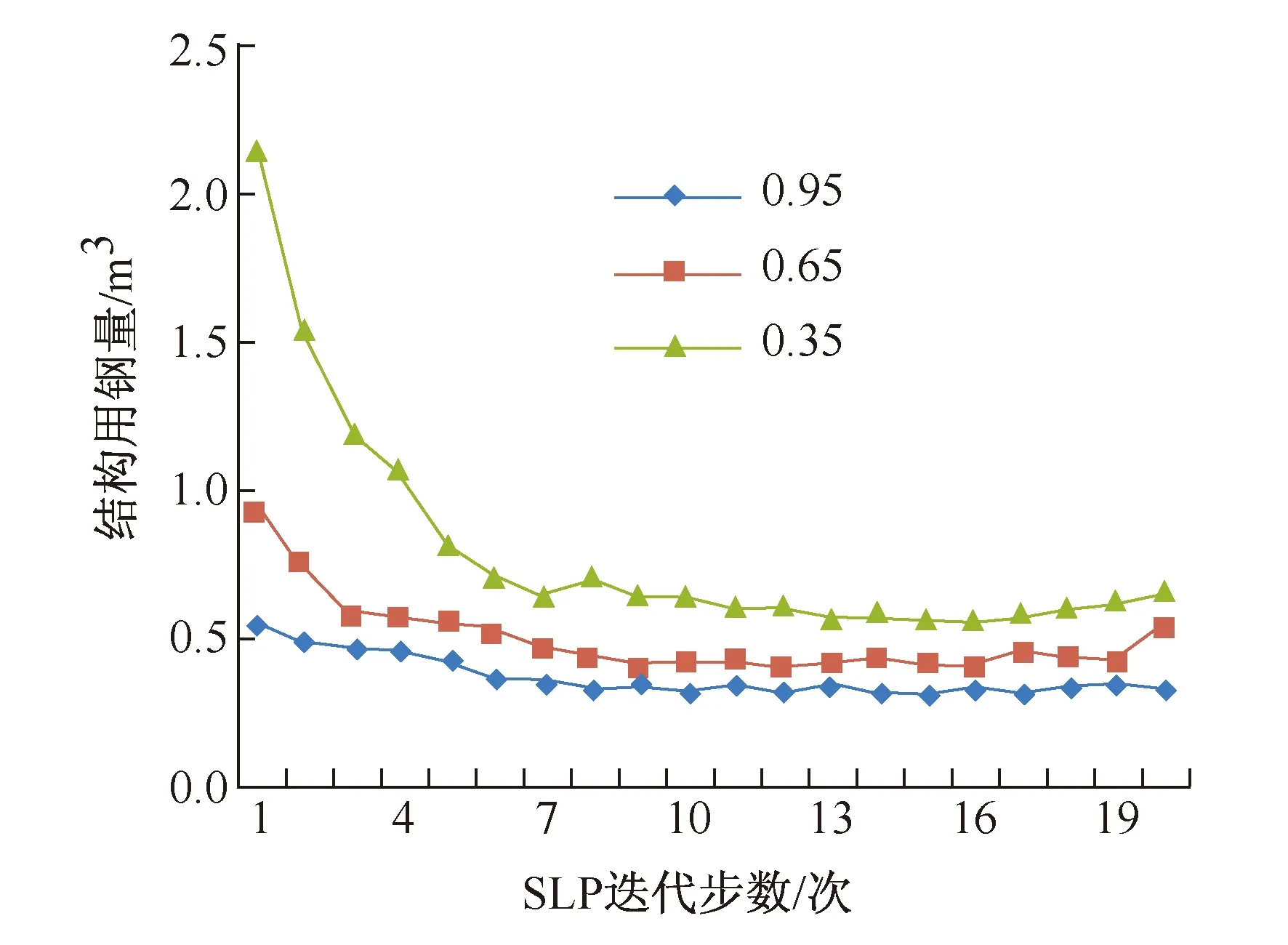
图3 不同应力比约束下的优化曲线Fig. 3 Optimization performance of the 1st Model underdifferent stress constraints

表1无位移约束时层间位移角

Table1Ratioofstorey-driftwithoutconstraints1/rad

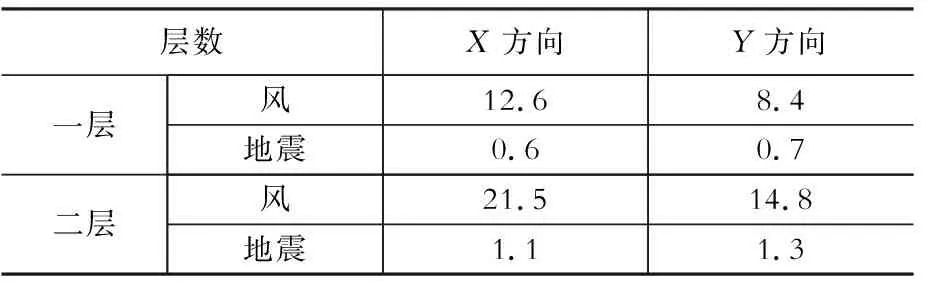
层数X方向Y方向一层风12.68.4地震0.60.7二层风21.514.8地震1.11.3

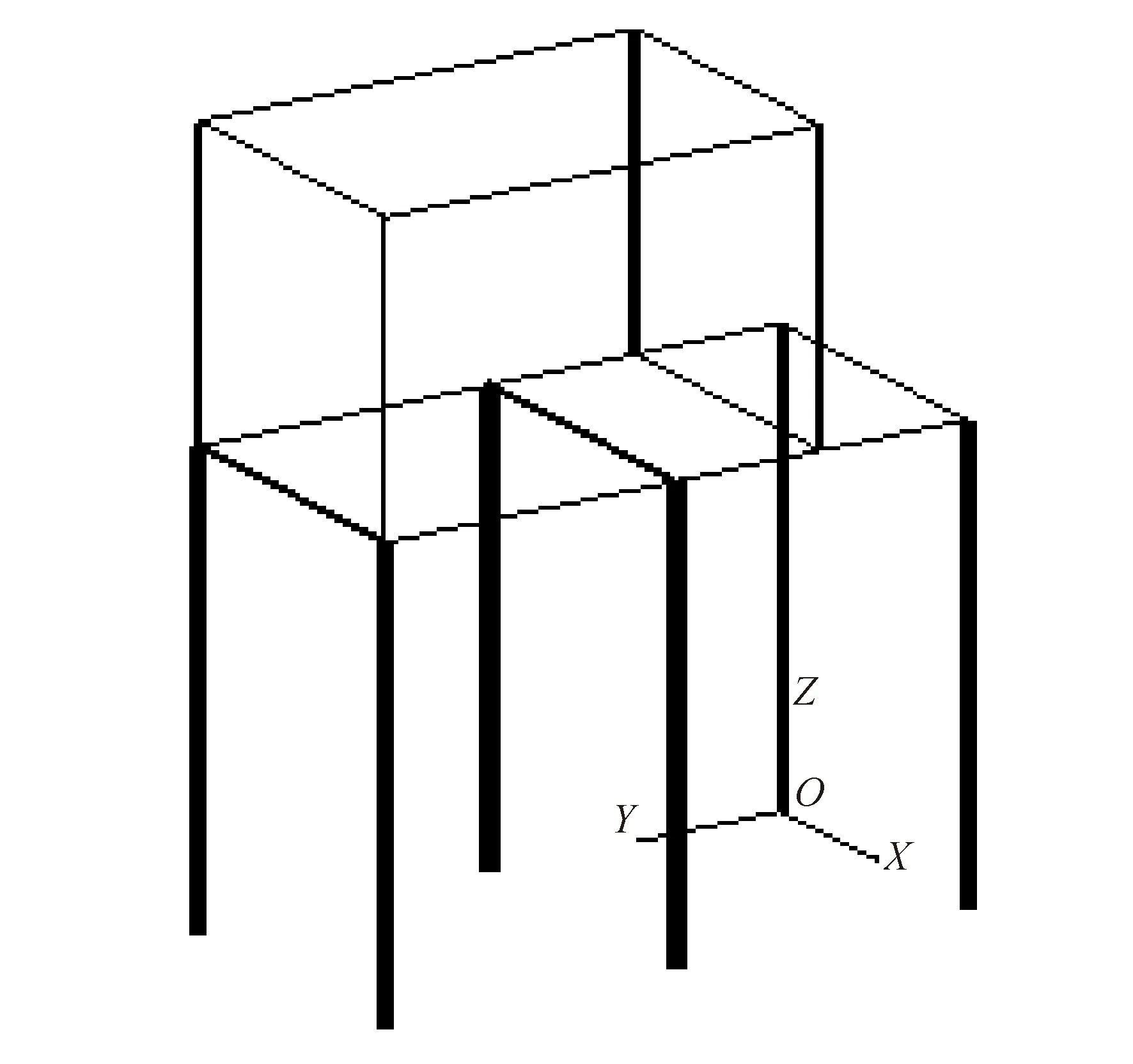
图4 算例一优化宏观效果图Fig.4 Macroscopic optimization effect of the 1st Model

图4显示，在最小用钢量目标的驱使下，杆件的截面尺寸表现出差异性。

表1显示，在无位移约束下，结构在风荷载作用下一、二层位移角均已超过规范限值2.5%。

然后对一层施加位移角约束条件，允许层间位移角风荷载下取2.5%，地震作用下取4%，优化后最小用钢量为0.491 m3，杆2达到最大应力比0.921，结构层间位移角列于表2。

表2仅一层位移角约束时层间位移角

Table2Ratioofstorey-driftunder1ststorey-driftconstraints%

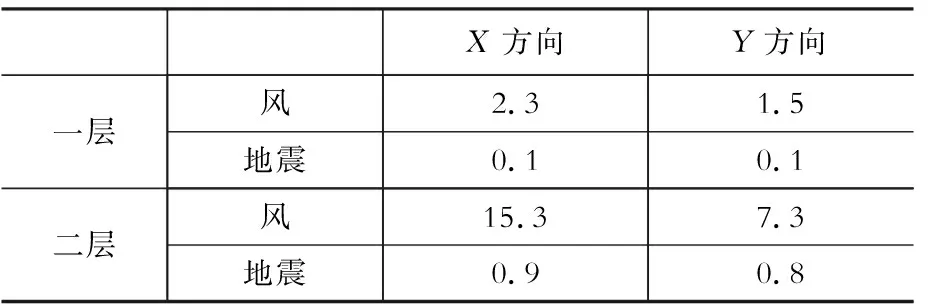
X方向Y方向一层风2.31.5地震0.10.1二层风15.37.3地震0.90.8

表2显示，一层在风荷载、地震作用下X方向层间位移角分别为2.3%、0.1%，满足约束条件2.5%、4%，而二层位移角未施加约束条件，在算法追求最小用钢量的过程中自由变化，最高达到15.3%。

可以看到此时虽然是一层风荷载下位移约束起控制作用，但应力比最大仍可接近限值0.95。

最后对一、二层均施加位移角约束，优化后最小用钢量为0.528 m3，杆1达到最大应力比0.941，结构层间位移角列于表3。

表3一、二层位移角约束时层间位移角

Table3Ratioofstorey-driftunderconstraintsofbothstories1/rad

层数X方向Y方向一层风1.71.8地震0.10.2二层风2.01.6地震0.20.2

表3显示，施加位移约束条件之后，结构一层在风荷载作用下X、Y方向层间位移角为1.7%、1.8%、二层在风荷载作用下X、Y方向层间位移角为2.0%、1.6%，均已满足规范2.5%要求。

通过算例一的一个不规则简单框架查看了优化算法和程序同时对应力、位移约束条件进行主动控制的效果。通过放大、缩小约束条件，在数值上验证了程序的正确性和符合逻辑性。

4.2 算例二

算例二为一个规则二层主次梁钢框架结构体系，平面布置如图5所示，柱距6 m，层高4 m。楼面恒载、活载均取4 kN/m2。

图5中未注明标签的构件均为次梁，不进行优化，只参与结构分析，且两端释放转角自由度。

应力比约束取0.95，层间位移角约束风荷载下取2.5%，地震作用下取4%，风荷载下柱顶位移约束取H/500，H为结构高度8 m。优化前后结构总体情况列于表4，构件尺寸列于表5，优化后结构最大层间位移角列于表6，优化的宏观效果见图6。

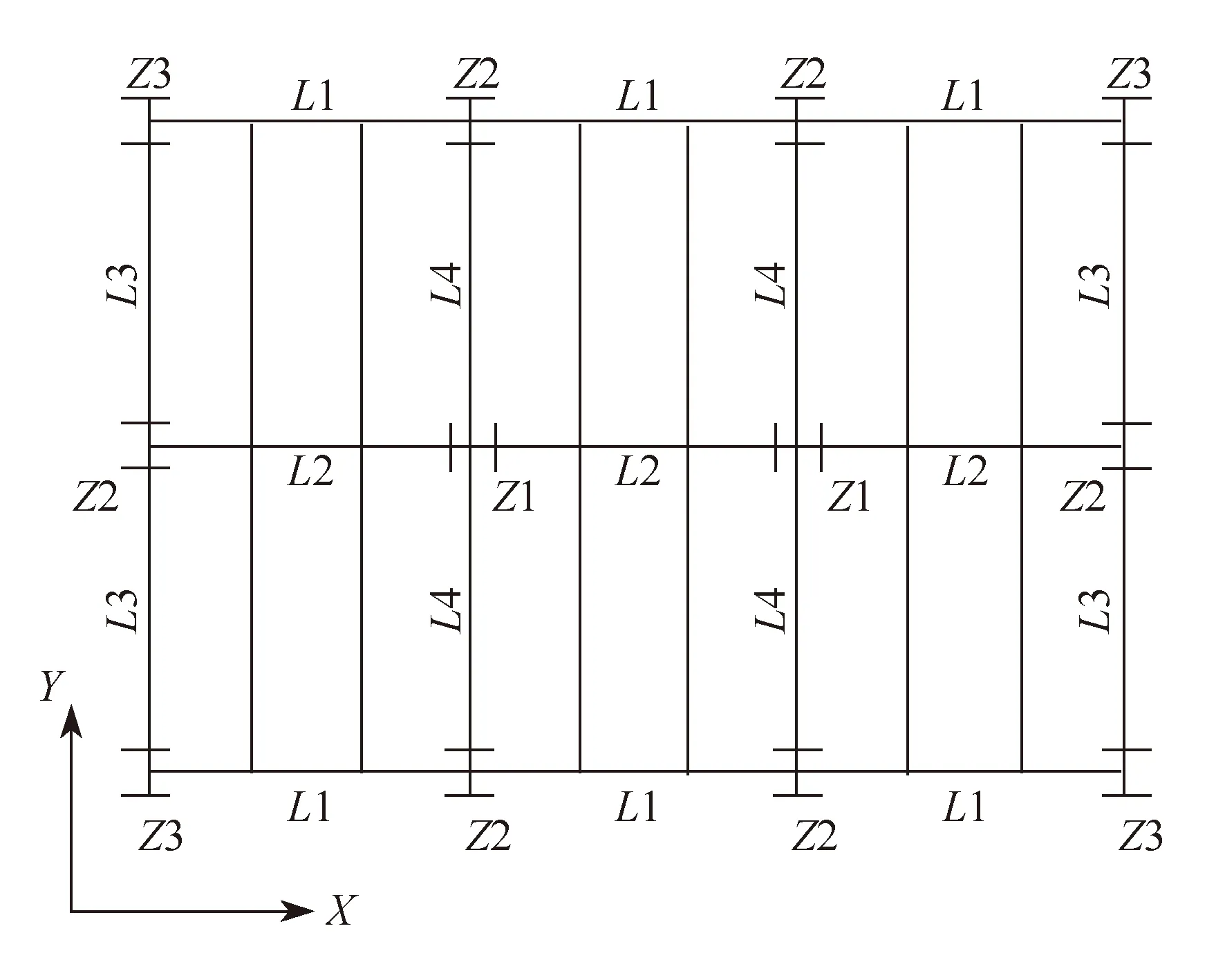
图5 算例二结构示意图Fig.5 The 2nd Model

表4算例二优化前后总体情况

Table4Macroscopicconditionsofthe2ndModelbeforeandafteroptimization

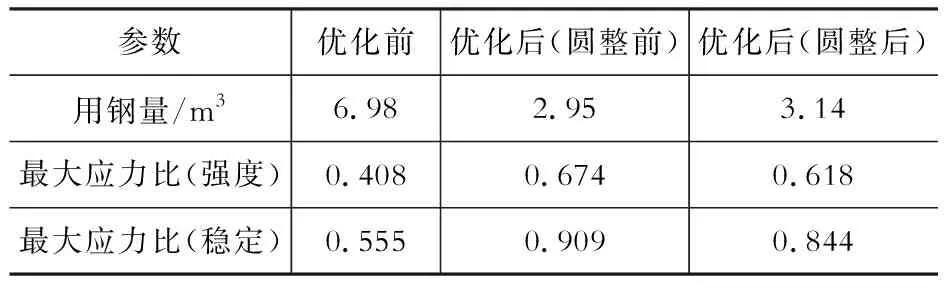
参数优化前优化后(圆整前)优化后(圆整后)用钢量/m36.982.953.14最大应力比(强度)0.4080.6740.618最大应力比(稳定)0.5550.9090.844

表5算例二优化前后构件尺寸

Table5Membersizesofthe2ndModelbeforeandafteroptimizationmm

表6算例二优化后层间位移角

Table6Ratioofstorey-driftofthe2ndModelafteroptimization

层数X方向Y方向圆整前圆整后圆整前圆整后一层风0.64%0.57%0.64%0.57%地震2.13%1.91%2.13%1.91%二层风0.52%0.47%0.52%0.47%地震0.23%2.05%0.23%2.05%

图6 算例二优化宏观效果图Fig.6 Macroscopic optimization effects of the 2nd Model

表4、表5、图6显示，优化过程自动使结构应力比在满足约束条件情况下得到释放。在初始截面的基础上，程序自动搜索最优截面尺寸，构件翼缘宽度及截面高度在最小用钢量的驱使下自动变化。

表6显示，结构优化后地震作用下层间位移角X及Y方向几乎一致，一层1.91%，二层为2.05%，说明优化程序在两个方向上同时对抗侧刚度进行了主动调整，使用钢量在约束条件之内趋于最低。

观察表4、表6中构件圆整前后情况，进行截面圆整后结构最大应力比为0.844，最大层间位移角为2.05%，与圆整前的结构响应比较有所降低，与限值0.9、4%相比较则仍有富余。因此，考虑到优化程序的精确度和优化后构件尺寸的圆整，在进行优化时，可适当放大约束条件的值。

5 结 语

(1) 本文基于序列线性规划和对偶仿射尺度法，以结构最小用钢量为优化目标，以构件截面尺寸为优化变量，推导了空间钢框架结构在强度、稳定性、节点位移、结构层间位移约束下整体优化的有限元模型，编制了程序。

(2) 通过一个简单二层不规则钢框架算例验证了优化程序同时处理应力与位移约束的可行性；收缩约束条件，验证了程序处理不同应力、位移约束的效果。

(3) 对一个主次梁体系钢框架结构模型进行优化，同时考虑规范对于构件强度、稳定性，结构层间位移角及柱顶侧移的限制，证明了优化算法和程序能够满足工程实际的需要。

[ 1 ] 赵赤云.钢结构住宅的现状及其综合经济效益分析[J].北京建筑工程学院学报, 2004, 20(2): 20-23.

Zhao Chiyun. The existing application of steel construction residence and analysis of comprehensive economic benefit for it [J]. Journal of Beijing University of Civil Engineering and Architecture, 2004, 20(2): 20-23. (in Chinese)

[ 2 ] 张雯雰,李丽娟,滕少华,等. 粒子群优化算法在离散变量结构优化中的应用[J]. 结构工程师, 2010, 26(2): 76-82.

Zhang Wenfen, Li Lijuan, Teng Shaohua, et al. Particle swarm optimizer algorithm for design optimization of structures with discrete variable [J]. Structural Engineers, 2010, 26(2): 76-82. (in Chinese)

[ 3 ] 杜剑明,张维声,郭旭. 基于SAND列式的桁架结构优化问题序列线性规划算法[J]. 工程力学, 2012, 29(3): 21-26.

Du Jianming, Zhang Weisheng, Guo Xu. Sequential linear programming algorithm based on the sand formula for truss optimization [J]. Engineering Mechanics, 2012, 29(3):21-26. (in Chinese)

[ 4 ] 朱杰江,罗峰.基于强度和变形约束的钢桁架优化[J]. 钢结构, 2012, 27(3): 11-16.

Zhu Jiejiang, Luo Feng. Steel-truss optimization based on strength and deformation constraints [J]. Steel Construction, 2012, 27(3): 11-16. (in Chinese)

[ 5 ] 宫海,李国强.多高层建筑钢结构实用优化方法研究[J]. 结构工程师, 2006, 22(1):1-5.

Gong Hai, Li Guoqiang. Practical optimization method for structural design of multi and tall steel buildings[J]. Structural Engineers, 2006, 22(1):1-5. (in Chinese)

[ 6 ] Stojan K, Goran T, Simon, et al. Optimal design of single-story steel building structures based on parametric MINLP optimization [J]. Journal of Constructional Steel Research, 2013(81): 86-103.

[ 7 ] Kaveh A, Farahmand Azar B, Hadidi A, et al. Performance-based seismic design of steel frames using ant colony optimization [J]. Journal of Constructional Steel Research, 2010, 66(4): 566-574.

[ 8 ] Kaveh A, Talatahari S. An improved ant colony optimization for the design of planar steel frames[J]. Engineering Structures, 2010, 32(3): 864-873.

[ 9 ] 黄冀卓,王湛.钢框架支撑体系连续型拓扑优化设计[J].工程力学, 2010, 27(11):106-112.

Huang Jizhuo, Wang Zhan. Continuum structural topology optimization for layout design of steel frame bracing systems[J]. Engineering Mechanics, 2010, 27(11):106-112. (in Chinese)

[10] 李炜. 线性优化及其扩展[M]. 北京: 国防工业出版社, 2011.

Li Wei. Linear optimization and its extension[M]. Beijing: National Defense Industry Press, 2011. (in Chinese)

[11] 中华人民共和国建设部. GB 50017—2003 钢结构设计规范[S]. 北京: 中国计划出版社, 2003.

Ministry of Construction of the People’s Republic of China. GB 50017—2003 Code for design of steel structures[S]. Beijing: China Planning Press, 2003. (in Chinese)

[12] 中华人民共和国建设部. GB 50011—2010 建筑抗震设计规范[S]. 北京:中国建筑工业出版社, 2010.

Ministry of Construction of the People’s Republic of China. GB 50011—2010 Code for seismic design of buildings[S]. Beijing: China Architecture and Building Press, 2010. (in Chinese)

[13] 中华人民共和国建设部. JGJ 99—98 高层民用建筑钢结构技术规程[S]. 北京:中国建筑工业出版社, 1998.

Ministry of Construction of the People’s Republic of China. JGJ 99—98 Technical specification for steel structure of tall buildings[S]. Beijing: China Architecture and Building Press, 1998. (in Chinese)