北斗与GPS随机模型对比分析

王俪霏，李博峰，张兴福

(1.同济大学 测绘与地理信息学院，上海 200092；2.广东工业大学 测绘工程系， 广东 广州 510006)

北斗与GPS随机模型对比分析

王俪霏1，李博峰1，张兴福2

(1.同济大学 测绘与地理信息学院，上海 200092；2.广东工业大学 测绘工程系， 广东 广州 510006)

针对两段北斗/GPS双系统的短基线，对比分析北斗B1和B2、GPS的L1和L2频率上伪距和相位的观测值精度、卫星精度与高度角的关系，以及不同类型观测值之间的交叉相关性。结果表明：北斗短基线观测精度与GPS精度相当，北斗系统的MEO卫星的观测精度最高，其次为IGSO和GEO卫星；北斗与GPS的精度与高度角存在不同程度的相关性；采用的接收机北斗B1和B2、GPS的L1和L2频率上的相位观测值存在弱相关，其他类型的交叉相关性不明显。

北斗；GPS；观测精度；高度角；交叉相关性

为了提高卫星导航定位的安全性、独立性和自主性，我国于20世纪80年代决定建设独立自主的卫星导航系统[1]。2000年，北斗导航试验系统建成，标志着我国成为第3个拥有自主卫星导航系统的国家。自2012年12月27日开始，北斗二代卫星导航系统正式向亚太大部分地区独立提供连续服务，定位精度水平方向优于10 m，测速精度优于0.2 m/s，授时精度优于50 ns，并计划于2020年左右形成全球覆盖能力[2]。

截止目前，北斗系统已发射5颗GEO、5颗IGSO和4颗MEO卫星。对于北斗系统的研究主要集中在定位定轨、北斗与GPS、GLONASS等系统组合定位应用、北斗系统的信号结构以及其在各领域中的应用等方面[3-7]。在随机特性方面，GPS系统的高度角模型、自相关性、交叉相关性等方面已有诸多研究成果[8-10]，但对于北斗系统，大多通过分析电离层、信噪比和多路径效应等方面的误差得到北斗系统的精度[11-12]。本文借鉴以往GPS零/短基线的方法，通过对北斗与GPS双系统的短基线进行差分和重组，提取出观测值的随机噪声，并运用随机观测噪声分别分析北斗与GPS系统两个频率上的观测值精度、精度与高度角的关系以及不同观测类型之间的交叉相关性，并对两个系统的结果进行对比分析。

1 基于已知基线的随机特性分析

对于短基线，忽略残余的对流层、电离层和多路径等误差的影响，历元t北斗和GPS的伪距和相位观测值的站间单差观测方程均可以表示为[9]

(1)

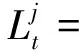
(2)

由于基线已知，且短基线的双差模糊度单历元即可以较高的成功概率固定，则式(1)、式(2)可以整理为

(3)

(4)

(5)

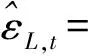
短基线两端采用同类型接收机，则两测站的非差观测值可近似地认为等精度，以相位观测值为例，导出历元t的非差观测值精度为

(6)

对于每个历元来说，不同卫星对应不同的高度角，需要单颗卫星的观测值残差来分析观测值精度与卫星高度角的关系。由于高度角在短时间内的变化较小，连续观测n个历元，可得到卫星j的非差相位观测值精度

(7)

不同类型的观测值之间的相互关系，称为交叉相关性，用相关系数ρ来衡量。以同一系统两个频率上的相位观测值为例

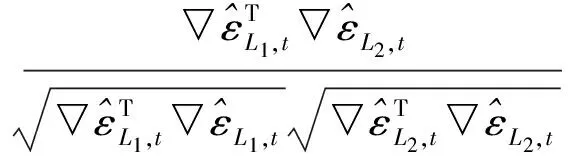
(8)

其他类型观测值间的交叉相关性计算公式类似可得。

2 算例分析

本文分别给出两个时间段内不同短基线的计算结果。算例1采用和芯星通UR240接收机采集的2012年11月13日至15日共3 d的观测数据，采样间隔为1s，基线长度约为470.3 m，北斗系统的观测类型为B1和B2频率上的伪距和相位观测值，GPS的观测值类型为C1、P2、L1和L2，截止高度角取10°。算例2为采用相同接收机采集的2013年6月21日至23日共3 d的观测数据，采样间隔为1s，基线长度为1.772 m，北斗与GPS的观测值类型与算例1相同，截止高度角取10°。

表1、表2为算例1中北斗和GPS的观测值精度及交叉相关性。表3、表4为算例2对应的结果，其中对角线元素为观测值精度，非对角元素为不同类型观测值之间的交叉相关性。从计算结果可以看出，算例1中，北斗系统的伪距精度为0.3～0.4 m，相位精度为4～5mm，其中B2频率上相位精度略优于GPS的L2精度；算例2中，伪距精度为0.2～0.3 m，相位精度为2～3 mm，明显优于算例1的精度，这是由于算例1基线较长，残余的多路径效应使得观测误差较大。总体来说，北斗系统的观测值精度与GPS基本处于同一水平。B1和B2频率上相位观测值和GPS的L1和L2分别存在比较明显的交叉相关性，存在其他类型观测值之间的相关性不明显，可以忽略不计。

表1 北斗观测值精度及交叉相关性(伪距单位：m，相位单位：mm)

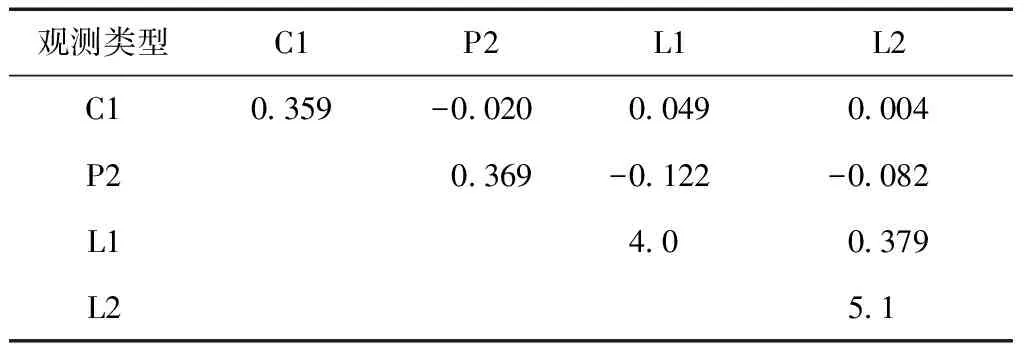
表2 GPS观测值精度及交叉相关性(伪距单位：m，相位单位：mm)

表3 北斗观测值精度及交叉相关性(伪距单位：m，相位单位：mm)

表4 GPS观测值精度及交叉相关性(伪距单位：m，相位单位：mm)

表5、表6分别给出了两段基线的北斗系统GEO、IGSO、MEO卫星的观测值精度。由于单历元各类卫星数目较少，所以采用连续10个历元的观测数据进行计算。从结果可见，4类观测值的MEO卫星观测精度最高，伪距在0.3 m之内，算例1的相位精度在4 mm之内，算例2的相位精度在2 mm之内，而IGSO卫星的精度又都略优于GEO卫星的精度。

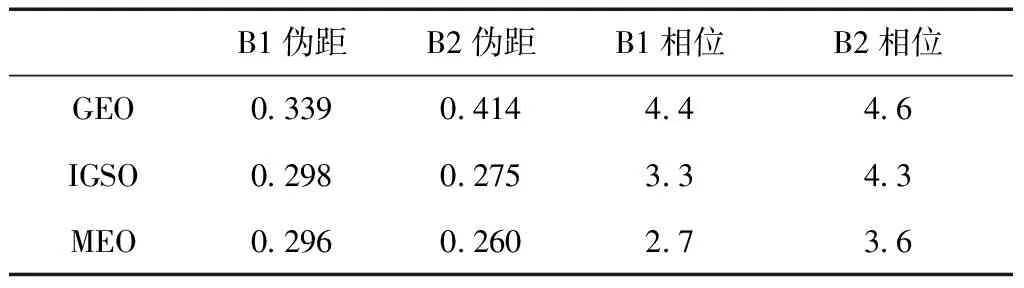
表5 北斗系统GEO、IGSO和MEO卫星观测值精度(伪距单位：m，相位单位：mm)

表6 北斗系统GEO、IGSO和MEO卫星观测值精度(伪距单位：m，相位单位：mm)

为了得到观测值精度与卫星高度角的关系，采用连续10个历元的数据，按式(7)计算得到北斗与GPS观测值的精度，除去异常值后各个高度角上对应多个精度估计结果，取平均值作为该高度角对应的观测精度。图1、图3为两段基线北斗系统观测值精度与高度角的关系，依次为B1频率伪距、B2频率伪距、B1频率相位和B2频率相位；图2、图4为两段基线GPS系统观测值精度与高度角的关系，依次为C1、P2、L1和L2。

图1 北斗不同类型观测值精度与高度角关系

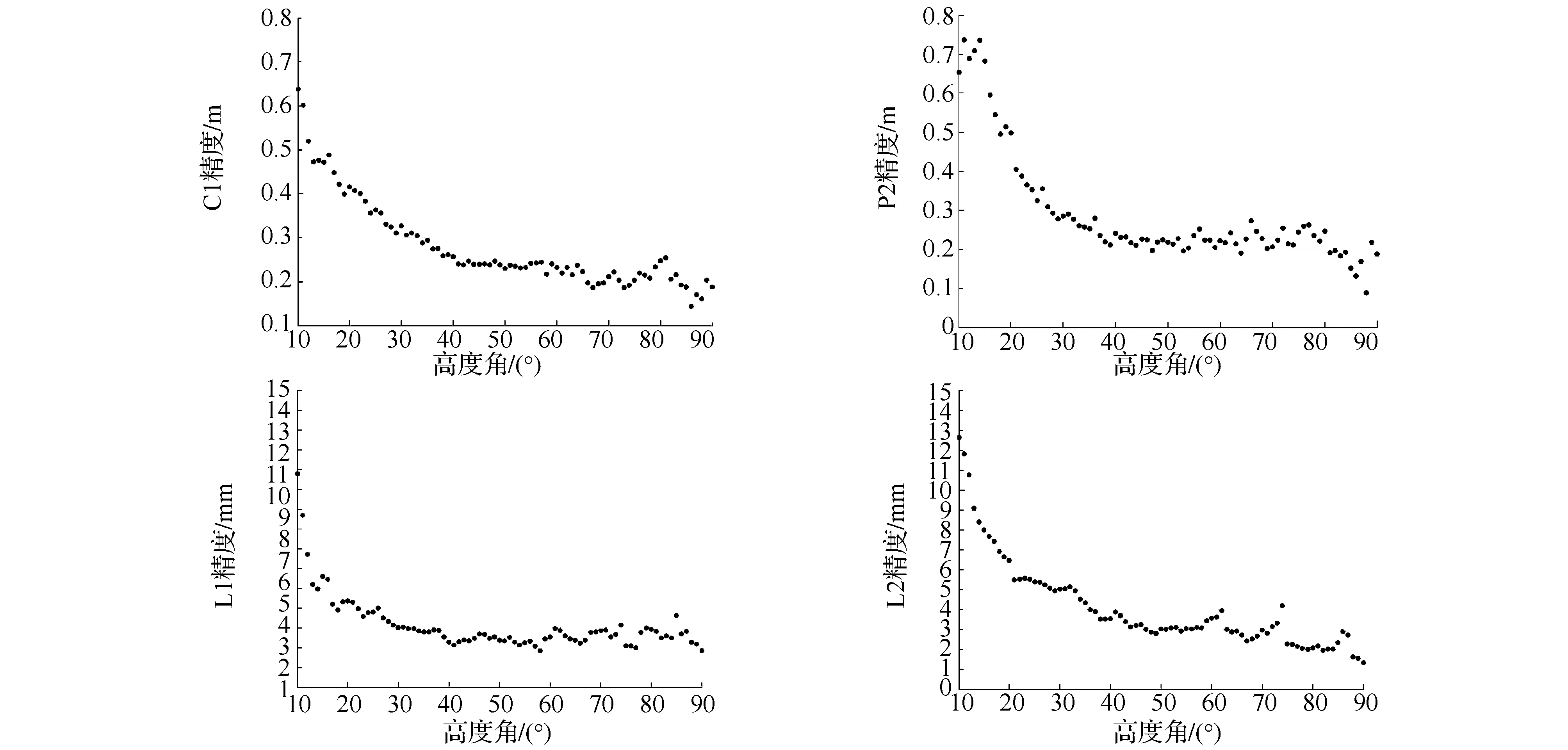
图2 GPS不同类型观测值精度与高度角

图3 北斗不同类型观测值精度与高度角关系

图4 GPS不同类型观测值精度与高度角

由图所示，北斗与GPS系统的所有类型观测值都与卫星高度角明显相关，即高度角越高，观测精度越好。算例1中，GPS系统的相关趋势较北斗系统平稳，这可能是由于GPS系统各个历元接收到的卫星数目相对稳定，而北斗系统每个历元的MEO卫星数目变化较大，GEO卫星数目稳定但精度较低，导致某些高度角上的精度估值本身较差。但在低高度角时，北斗系统的精度明显高于GPS系统的精度，这体现出了北斗系统的优越性。不同系统、不同类型的观测值精度与高度角的关系并不相同，对于北斗系统的伪距观测值来说，高度角低于20°时的精度是高度角高于80°时的精度的2倍，对于相位观测值则达到5倍。由此可见，用统一的高度角加权模型表示观测值与高度角关系的做法并不合理，在高精度定位时应根据实际情况确定合理的随机模型。

3 结 论

本文通过两段实测北斗与GPS短基线数据对比分析了两个系统各类卫星的观测值精度、精度与高度角的关系以及不同类型观测值之间的交叉相关性，结果表明：

1)对于短基线来说，北斗系统的观测精度与GPS精度相当，伪距精度为0.3～0.4 m，相位精度为2～4 mm；对于北斗系统来说，MEO卫星观测值精度最高，其次为IGSO卫星和GEO卫星。

2)北斗与GPS系统的观测精度均与卫星高度角相关，高度角越高，观测精度越好；不同系统、不同类型观测值的精度与高度角的相关趋势各不相同。

3)对于本文采用的接收机，北斗B1和B2频率上的相位观测值以及GPS的L1和L2相位观测值分别存在弱相关，其他类型观测值的相关性不明显，可以忽略不计。

[1]杨元喜.北斗卫星导航系统的发展、贡献与挑战[J].测绘学报，2007，37(2)：195-197.

[2]谢军.北斗导航卫星的技术发展及展望[J]. 中国航天，2013(3)：7-11.

[3]Ma X Y，Shen Y Z. BeiDou positioning and multipath analysis for short baselines[C]. China Satellite Navigation Conference(CSNC) 2013 Proceedings Lecture Notes in Electrical Engineering Volume 243，2013:447-458.

[4]高星伟，过静珺，程鹏飞,等.基于时空系统统一的北斗与GPS融合定位[J].测绘学报，2012，41(5)：743-748.

[5]王光鼎，张升康，杨汝良.基于北斗无源与GLONASS导航系统的卫星组合导航用于位置计算[J].测绘学报，2007，36(4)：377-382.

[6]范本尧，李祖洪，刘天雄.北斗卫星导航系统在汶川地震中的应用及建议[J]. 航天器工程，2008，17(4)：6-13.

[7]丁昊，谭美景，王万历，等.北斗数据接入中间件的设计与实现[J].测绘工程，2013,22(3)：20-23.

[8]P BONAona. Precision, cross correlation，and time correlation of GPS phase and code observations[J]. GPS Solution，2000，4(2)：3-13.

[9]Li B F，Shen Y Z，Xu P L. Assessment of stochastic models for GPS measurements with different types of receivers[J]. Chinese Science Bulletin，2008，53(20)：3219-3225.

[10]李博峰，沈云中，楼立志. GPS中长基线观测值随机特性分析[J].武汉大学学报：信息科学版，2010，35(2)：176-180.

[11]李文文，李敏，胡志刚,等.北斗与GPS电离层模型对导航定位精度的比较分析[C].第四届中国卫星导航学术年会电子文集-S3精密定轨与精密定位,2013.

[12]程鹏飞，李玮，秘金钟.北斗导航卫星系统测距信号的精度分析[J].测绘学报， 2012，41(5)：691-695.

[责任编辑：刘文霞]

Comparative analysis of Beidou and GPS stochastic models

WANG Li-fei1, LI Bo-feng1, ZHANG Xing-fu2

(1. College of Surveying and Geo-Informatics, Tongji University, Shanghai 200092, China; 2. Dept.of Surveying and Mapping, Guangdong University of Technology, Guangzhou 510006, China)

In this contribution, it presents the stochastic characteristics of Beidou observations on both B1and B2 frequency compared with GPS counterparts. The studies include the observation precision and its elevation-dependence as well as the correlation between different observation types. The results show the observation precision of Beidou is comparable with GPS. The precision of MEO satellites is better than IGSO and GEO satellites. All the observation types of both Beidou and GPS are elevation-dependent with different extent. According to the receiver, the phase observations of Beidou B1and B2 as well as GPS L1and L2 are slightly correlated, whereas the cross correlations between the other observation types are not observed.

Beidou; GPS; observation precision; elevation-dependence; correlation

2013-10-10

国家自然基金资助项目(41074018，41104002)

王俪霏(1988-)，女，硕士研究生.

P228

：A

：1006-7949(2014)10-0009-05