时间序列分析在地铁沉降监测中的应用

张 松，田林亚

(河海大学 地球科学与工程学院，江苏 南京 210000)

时间序列分析在地铁沉降监测中的应用

张 松，田林亚

(河海大学 地球科学与工程学院，江苏 南京 210000)

采用时间序列分析的方法，通过对已获取的地铁沉降监测数据进行分析、建模，得到合理的沉降预测模型，不仅可以预测出短时间内地铁区段的沉降量，并可了解地铁区段短时间内的沉降趋势。实验证明，方法简单、快速、准确，具有良好的短期预报效果。

地铁；沉降监测；时间序列；数据处理；短期沉降预测

城市高层和地下建筑工程的施工过程中，通常都要开展沉降监测工作，掌握建筑物自身及其周边其它建筑物的沉降量和沉降速率，对沉降状况进行分析和评价，采用合理的数学模型和方法进行沉降预测，掌握沉降的发展趋势和变化规律。

目前，对于沉降监测成果的应用主要有以下几个方面：①掌握建筑物的沉降状态，调整施工进度或加强安全防范措施；②验证有关设计参数；③对数据进一步分析利用，对建筑物的沉降趋势进行预测[1-2]。建筑物沉降监测成果是按照时间顺序(或一定的空间顺序)相继发生的一组数据序列，具有3个特点:与时间相关，但不一定是时间的严格函数；带有一定的随机性，但彼此之间又具有一定的统计关系和统计规律；历史数据的相关性随着时间间隔的增大而减小。本文根据时间序列分析的基本方法，针对某城市地铁保护区的沉降监测数据，建立沉降预测时间序列模型，通过沉降预测掌握地铁结构短期的沉降发展趋势。

1 沉降时间序列建模与预测

1.1 时间序列的平稳性检验

沉降时间序列分为平稳时间序列和非平稳时间序列两类。平稳时间序列模型包括AR模型、MA模型、ARMA模型3类[3]，非平稳时间序列模型包括ARIMA模型和SARIMA季节模型。要建立合理的沉降时间序列模型，首先要对已有沉降时间序列的平稳性进行检验，这可以通过计算样本数据的自相关系数来检验其平稳性，计算公式为

(1)

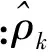
1.2 模型选择与定阶

如果沉降样本序列经检验为平稳序列，可进一步根据样本的自相关函数和偏自相关函数[4]进行模型的选择和定阶。若样本的自相关函数呈现拖尾状态，而偏自相关函数是p阶结尾，则选择AR(p)模型。

xt=φ0+φ1xt-1+φ2xt-2+…+φpx1+εt.

(2)

式中：xt为t时刻的观测值；εt为该模型的白噪声扰动项；φi(i=1, 2,…，p)为模型系数。

若样本的自相关系数q阶截尾，而偏自相关系数拖尾，则选择MA(q)模型。

xt=θ0εt-θtεt-1-θ2εt-2-…-θqεt-q.

(3)

当样本的自相关系数和偏自相关系数都拖尾时，则选择ARMA(p,q)模型。

xt=μ+φ1xt-1+…+φpxt-p+

εt-θ1εt-1-…-θqεt-q.

(4)

根据自相关和偏自相关系数进行模型的选择和定阶存在一定的主观性，通常情况下按照最小信息量准则AIC和SBC方法来选择最优模型,AIC和SBC的值越小，表明模型越精确。

AIC=Tln(RSS)+2n.

(5)

SBC=Tln(RSS)+nln(T).

(6)

式中:n为待估参数个数(p+q+可能存在的常数项)；T为可使用的观测值；RSS为残差平方和。

1.3 模型的参数估计与检验

时间序列模型的类型和阶数确定后，还要对模型参数进行估计，方法有矩估计、最小二乘估计和极大似然估计等[5]。模型检验是通过对提取信息后的残差序列进行检验，若拟合后模型的残差序列为不存在相关性的白噪声序列，则表明该拟合模型是最优的，拉格朗日乘数(LM)检验是检验残差序列是否存在高阶相关性的一种有效方法[6]。

如果误差项ut是p阶序列相关的，则ut=λ1ut-1+λ2ut-2+…+λput-p+εt。若要证明ut是任意阶不相关，则提出约束条件H0：λ1=λ2=…=λp=0。如果约束条件成立，LM服从χ2(p)分布。

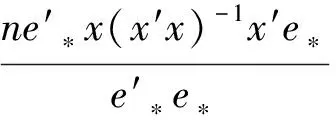
(7)

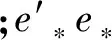
1.4 模型的预测

根据沉降观测样本序列{xk}建立的模型可以预测未来沉降xk+1…xk+m，当m=1时，称作一步预测，当m>1时，为多步预测[7]。ARMA模型的预测公式为

(8)

当系数θi(i=1,2，…，p)的值为0时，即为MA(q)的预测公式。

2 实例应用与分析

2.1 工程概况

表1为某城市地铁沉降监测数据，该地铁已经处于运行阶段，由于其附近建筑基坑的开挖，要求采用二等水准测量方法进行区段沉降监测，基坑的位置和监测点的布置如图1所示。

图1 沉降监测点布置图

本文采用靠近基坑中心的X11点的前14期沉降观测值作为样本数据，建模预测第15～20期的沉降量。

2.2 平稳性检验

前14期样本数据的自相关系数值如表2所示，当k增大时，自相关系数迅速趋于0，并在0值附近波动，表明该序列为平稳的时间序列。

表1 沉降观测值 m

表2 样本数据自相关系数值

2.3 模型的选择和求解

计算样本的偏自相关系数，和自相关系数一同绘于图2。由图2可以看出，样本数据的自相关系数在延迟3阶后，迅速趋于0，并在0附近波动，可认为三阶截尾。样本的偏自相关系数在0值附近一直有较大的波动，呈现拖尾状态。所以初步选定模型为MA(2)、MA(3)、MA(4)。

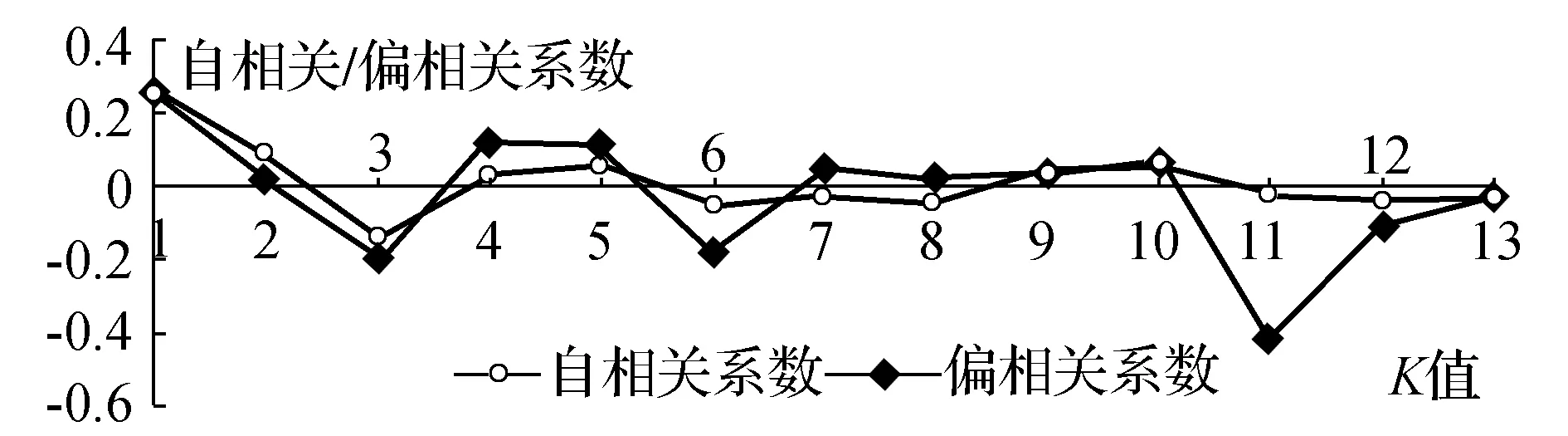
图2 自相关与偏自相关系数对比

根据AIC、SBC方法进行模型检验，结果如表3所示，其中MA(3)模型的AIC、SBC值最小，因此选择MA(3)模型。

表3 模型最优检验表

根据最小二乘估计法求得模型系数，得到MA(3)模型为

xt=-1.8553+0.06589εt-0.151470εt-1-

0.906 946εt-2.

(9)

2.4 模型参数检验与预测

根据求得的模型对X11点的第15～20期的沉降量进行预测，预测方法包括1步循环预测、2步预测和3步预测，预测值及其与实测值的残差如表4所示。

表4 预测值及其与实测值的残差

根据表3可以得出如下结论：1步预测法精度最高，3步预测法精度最低；随着步数的增加，残差变大，并且预测值在常系数值附近波动(本例模型常系数值为-1.8553)，可见时间序列的短期预测效果较好；3步以内的沉降预测都具有良好的效果。

3 结束语

本文研究了时间序列分析方法在建筑物沉降监测中的应用。结合地铁保护区沉降监测数据，采用时间序列分析的方法，通过对沉降量的计算与分析，得出该地铁区段的沉降量为平稳时间序列，并进一步进行建模和预测，获得较高的预测精度和较好的预测效果，说明利用时间序列模型进行沉降预测是完全可行和有效的，所建沉降预测模型能很好地反映地铁区段的沉降变化规律。除此之外，沉降监测中还密切注意基坑附近的水位变化[8-9]、地铁上方的材料堆积和地铁内部的渗漏裂缝等，为掌握地铁区段的沉降状态和地铁安全运营起到保障作用。

[1]黄声享.变形监测数据处理[M].武汉：武汉大学出版社, 2003.

[2]兰孝奇.建筑物沉降的时间序列分析与预报[J]. 河海大学学报, 2006,34(4):426-429.

[3]朱睿, 张俊中, 龙洋. 时间序列模型在建筑物沉降监测中的应用[J]. 测绘与空间地理信息, 2012, 35(2):213-216.

[4]石玉峰，孙保奇.时间序列分析及其在变形数据分析中的应用[J].金属矿山, 2004(2):13-14.

[5]刘华夏.基于时间序列分析的地铁变形监测数据建模与预报研究[J].铁道勘察, 2009,17(3):17-19.

[6]钱争鸣.非线性时序模型LM检验的两类临界值检验统计功效对比[J]. 数量经济技术经济研究, 2006(1):99-105.

[7]石双忠.时序分析在变形监测数据处理中的应用[J].工程勘察,2004,32(3):59-67.

[8]郑立常, 卫建东，郑俊锋，等. 基坑施工对邻近运营地铁隧道影响监测的实践[J]. 测绘工程, 2007,16(2):47-49.

[9]周小莉，俞荭.信息化测绘条件下的地铁施工监测方法探讨[J].测绘工程，2014，23(9)：35-39.

[责任编辑：张德福]

Application of time series analysis to metro subsidence monitoring

ZHANG Song, TIAN Lin-ya

(School of Earth Sciences and Engineering,Hohai University, Nanjing 210000, China)

The time series analysis method is used to analysis the metro-subsidence monitoring data and to establish a reasonable model. Not only can the value of the subsidence monitoring be forcast, but also can grasp the subsidence trends of the metro in short time. Experiments prove that the method is simple, rapid, precise and has a good short-term forecasting results.

metro;subsidence monitoring; times series; data processing; short-term subsidence prediction

2013-08-25，2014-09-28补充更新

张 松(1989-)，男，硕士研究生.

TU196

：A

：1006-7949(2014)10-0063-04