一类两神经元时滞神经网络稳定性和Hopf分支
2014-08-22毕殿杰孙玉涛
毕殿杰,孙玉涛
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233030)
0 引言
神经网络是一个十分复杂的动力学系统.自从八十年代初始Hopfield[1]首次利用微分方程组对神经网络模型进行描述并分析研究其动力学性质以来,国内外许多研究学者考虑到神经元之间信号传输的延迟,提出并研究了大量的具有时滞因素的神经网络模型[2-7]. 在文献[6]中,徐和何研究了如下具有两个神经元的时滞神经网络模型:
(1)
在模型(1)中,xi(t)(i=1,2)表示第i个神经元在时刻t的状态.f(xi)(i=1,2)表示两个神经元的连接函数,α1,α2,a,b,c和d为模型参数.τ1和τ2为两个神经元之间的信号传递延迟,且均为正常数.虽然在文献[6]研究了模型(1)的稳定性和Hopf分支,但是文献[6]作者只是以τ1与τ2二者之和为分支参数讨论的.本文研究更一般的情形,利用τ1与τ2两个时滞的不同组合为分支参数,讨论不同情形下的稳定性和Hopf分支问题.
1 Hopf分支存在性
为了方便讨论,首先给出如下假设:(H1)f∈C2(R),f(0)=0,且uf(u)>0(u≠0).基于以上假设易知,E*(0,0)是系统(1)的平衡点.将系统(1)在平衡点E*(0,0)处线性化,得到,
(2)
进而,得到系统(2)在平衡点E*(0,0)处的特征方程
λ2+A1λ+A0+B0e-λ(τ1+τ2)=0.
(3)

情形(1).τ1=τ2=0.方程(3)变为
λ2+A1λ+A0+B0=0.
(4)
情形(2).τ1>0,τ2=0.方程(3)变为
λ2+A1λ+A0+B0e-λτ1=0.
(5)
令λ=iw1(w1>0)为方程(4)的根,得到
(6)
进而,可以得到
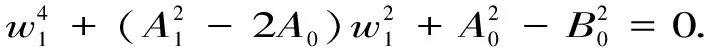
(7)
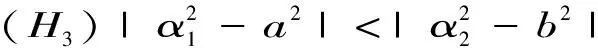
进而,由(6)可以计算
接下来,对横街性条件进行验证.对方程(5)的两端同时对τ1进行求导,得到
因此,
根据以上分析,以及文献[8]中的Hopf分支存在性定理,有下列结果.
定理2.1 对于系统(1),当τ1∈[0,τ10)时,平衡点E*(0,0)渐近稳定;当τ1=τ10时,系统(1)在平衡点E*(0,0)处产生Hopf分支.
情形3.τ1=0,τ2>0.方程(3)变为
λ2+A1λ+A0+B0e-λτ2=0.
(8)
对比方程(5)和方程(8),可以得到关于τ1=0,τ2>0时的下列结果
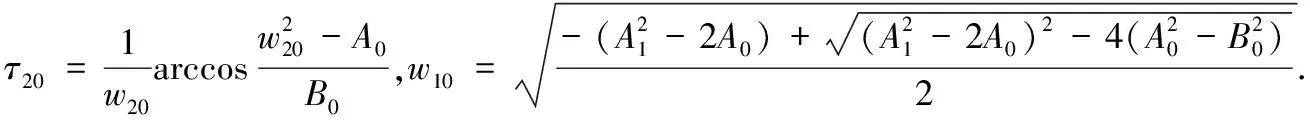
情形4.τ1=τ2=τ>0.方程(3)变为
λ2+A1λ+A0+B0e-2λτ=0.
(9)
令λ=iw(w>0)为方程(9)的根,有
(10)
进而得到
对方程(9)两边同时对τ求导,得到
进而,
根据以上分析,以及文献[8]中的Hopf分支存在性定理,有下列结果.
定理2.3 对于系统(1),当τ∈[0,τ0)时,平衡点E*(0,0)渐近稳定;当τ=τ0时,系统(1)在平衡点E*(0,0)处产生Hopf分支.
情形5.τ1>0,τ2>0且τ2∈(0,τ20).令λ=iw1*(w1*>0)为方程(3)的根,有
(11)
进而,得到
接下来,对横截性条件进行验证.在方程(3)的两边,同时对τ1进行求导,得到
因此,

根据以上分析,以及文献[8]中的Hopf分支存在性定理,有下列结果.

2 数字模拟
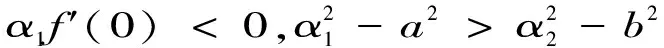
(12)

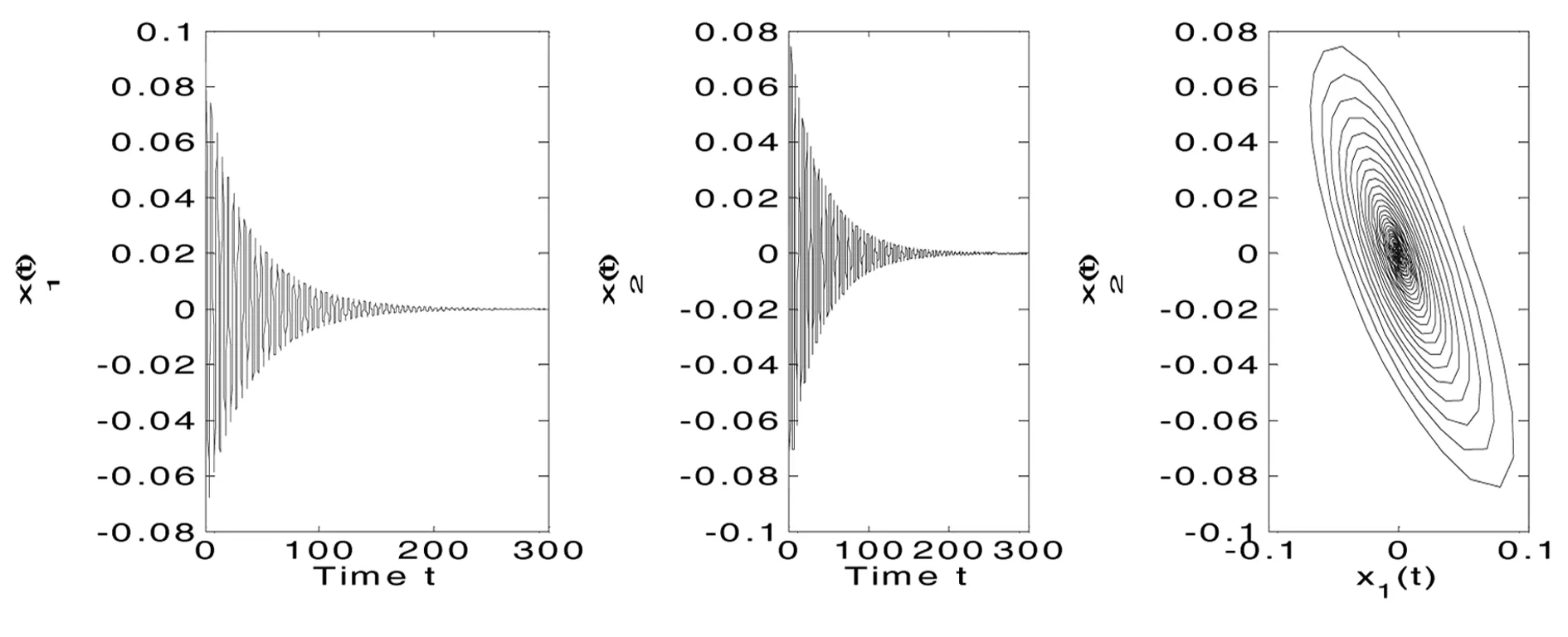
图1 当τ1=0.003<τ10时,系统(1)渐近稳定
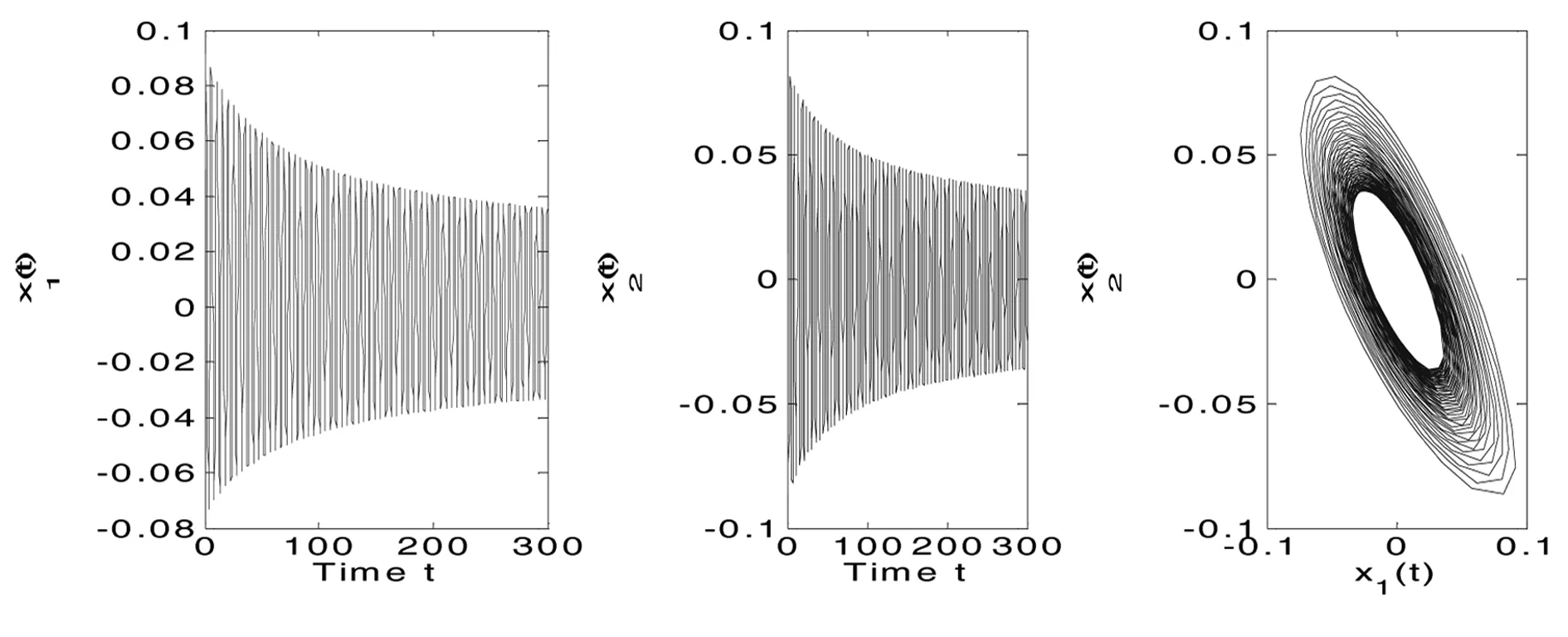
图2 当τ1=0.015>τ10时,系统(1)不稳定并发生Hopf分支
图3 当τ=0.0015<τ0时,系统(1)渐近稳定
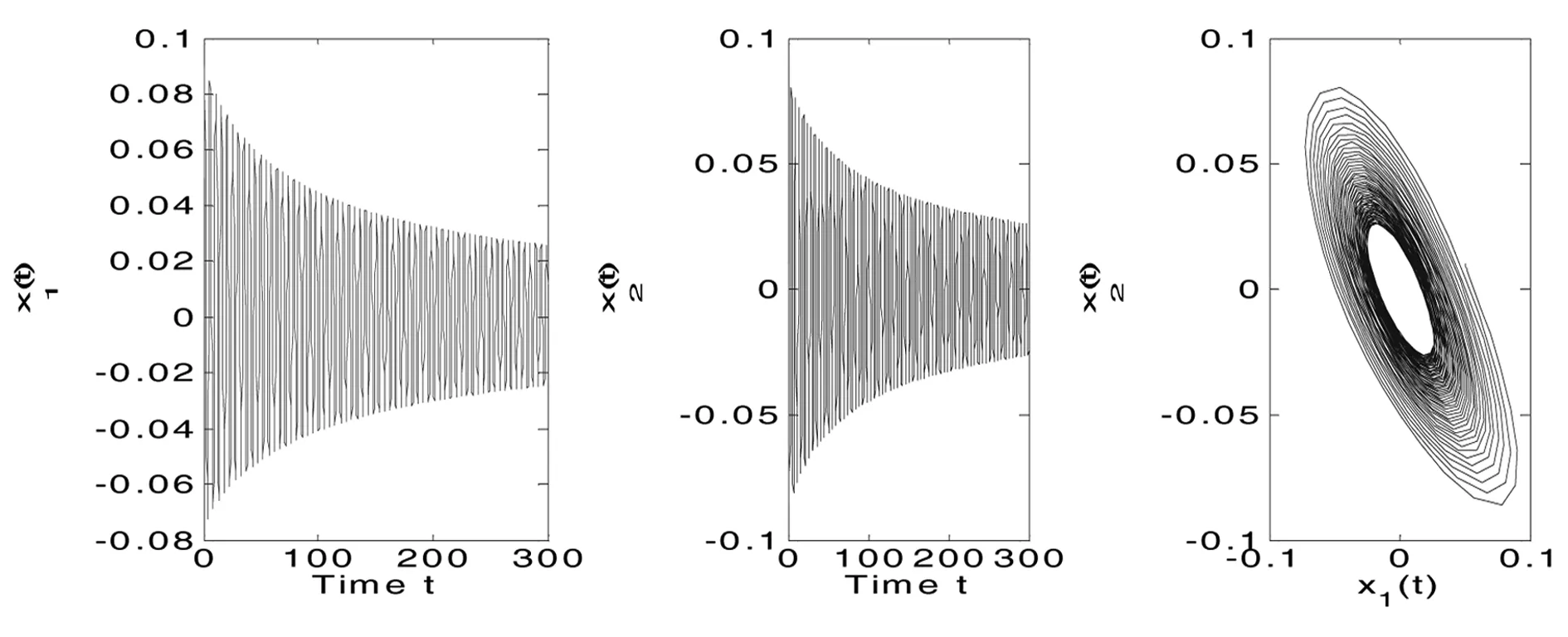
图4 当τ=0.007>τ0时,系统(1)不稳定并发生Hopf分支
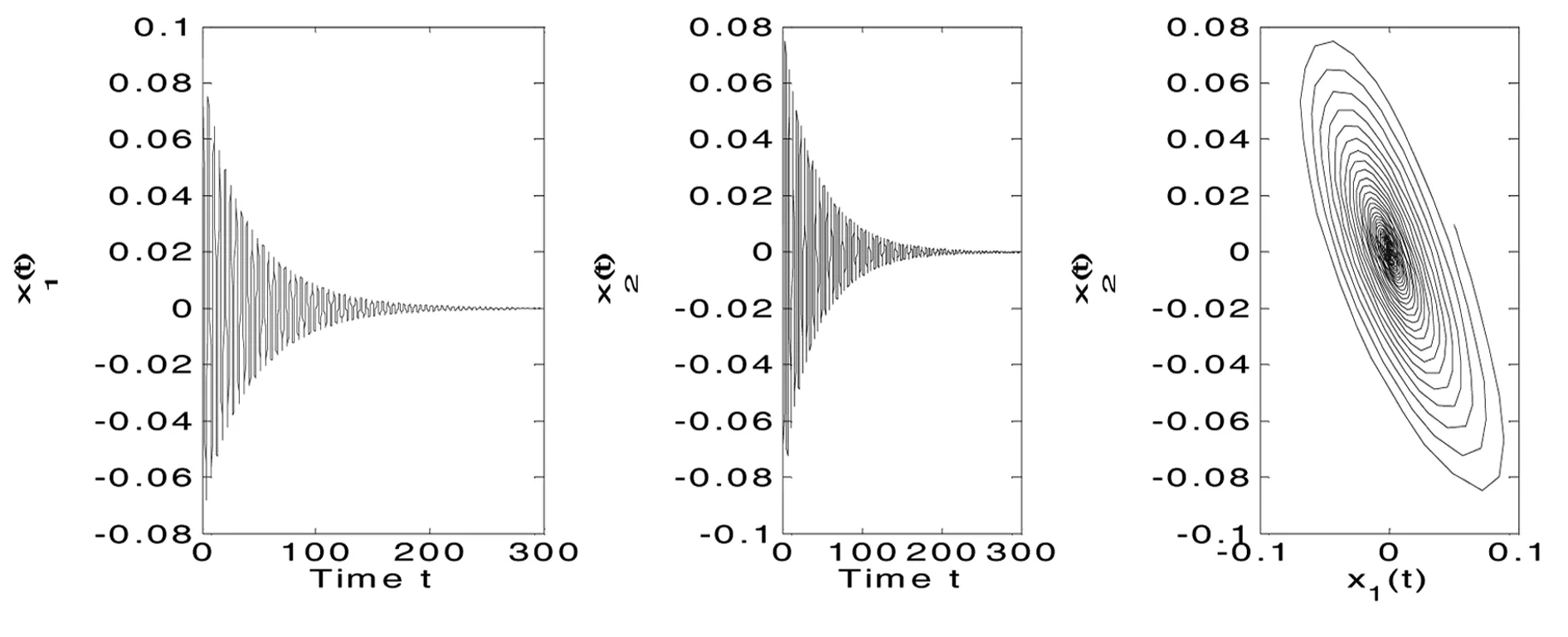
图5 当时,系统(1)渐近稳定
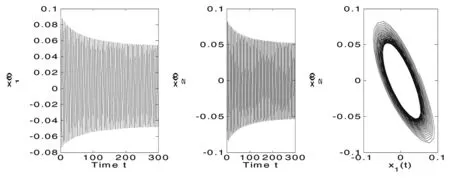
图6 当时,系统(1)不稳定并发生Hopf分支
3 结论
本文研究了一类具有时滞的神经网络模型.以两个时滞的不同组合作为分支参数,通过分析模型相应特征方程根的分布,确定了模型产生Hopf分支的充分条件.当时滞小于临界值时,模型渐近稳定.而一旦时滞的取值超过临界值,模型将失去稳定性并产生Hopf分支.最后,利用仿真实例验证了以上理论结果的正确性.对于Hopf分支的性质,有待进一步研究.
[1]Hopfield J J. Neurons with graded response have collective computational properties like those of two-state neurons[J]. Proceedings of the National Academy of Science USA, 1984, 81(10):3088-3092.
[2]唐长兵,一类具连续时滞二维神经网络模型的Hopf分支[J].曲阜师范大学学报,2007,33(1):54-58.
[3]徐昌进,姚凌云.具有时滞的神经网络模型的分支分析[J].华侨大学学报(自然科学版),2012,33(6):694-698.
[4]A.Hajihosseini, G. R. R. Lamooki, B. Beheshti, F. Maleki, The Hopf bifurcation analysis on a time-delayed recurrent neural network in the frequency domain[J]. Neurocomputing, 2010, 73(4-6):991-1005.
[5]S. Guo, Y. Yuan, Delay-induced primary rhythmic behavior in a two-layer neural network[J].Neural Networks, 2011, 24(1): 65-74.
[6]C.J.Xu, X.F. He. Stability and bifurcation analysis in a class of two-neuron networks with resonant bilinear terms [J]. Abstract and Applied Analysis, vol. 2011, Article ID 697630,21 pages,2011.
[7]B.X.Wang, J. G. Jian. Stability and Hopf bifurcation analysis on a four-neuron BAM neural network with distributed delays [J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15 (2) :189-204.
[8]Hassard B.D, Kazarinoff N.D. Wan Y.H.Theory and Applications of Hopf Bifurcation [M]. Cambridge University Press, Cambridge, 1981.
