耦合mKP方程的Lax对和分解

郭汉东

(郑州大学 西亚斯国际学院，河南 郑州 451150)

0 引言

一般来说，非线性偏微分方程的求解难度很大，只有在一些特殊的情况下才可能求得精确解，然而，对于孤子方程来说，已经有很多求精确解的方法.例如反散射方法[1]，双线性方法[2]，Painleve分析法[3]，代数几何法[4]，达布变换法[5]等.其中达布变换是一种自然而美妙的方法，利用此变换可以获得孤子方程的精确解.

本文主要内容是利用两个(2+1)维耦合mKP方程与它们分解后的(1+1)维KN方程之间的关系，即证明了KN方程的相容解就是耦合mKP方程的解.然后利用达布变换就能得到KN方程的精确解，进一步得到耦合mKP方程的解.

1 耦合mKP方程约化为KN方程

考虑下面的谱问题

(1)

辅助谱问题

(2)

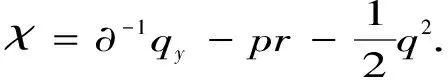
(3)

当λ=0时，方程(1)(2)可以化为方程(4)(5)

(4)

(5)

如果我们在位势间施加约束

q=4uv,p=2u2,r=2v2

(6)

结合(4)可得

(7)

把(6)(7)代入(4)(5)中，得到KN方程(8)(9)

(8)

(9)

由此可得如下命题.

2 KN方程的相容解就是耦合mKP方程的解

命题1 如果(u,v)是方程(8)(9)的相容解，则有(6)确定的函数(p,q,r)是方程(3)的解.

证明：利用(1.8)(1.9)得

qt=4uxxx+4uvxxx+24v(uvux+u3v2)x-24u(uvux-u2v3)x

pt=4uuxxx+12u(uvux-u3v2)x，rt=2vvxxx+12v(uvux-u2v3)x

qx=4uvx+4vux，qxx=4uvxx+4vuxx+8uxvx，

+8ux(v2u)x+48v2u(u2v)x+48u2v(v2u)x+24v2uuxx-24u2vvxx

rxxx=12vxvxx+4vvxxx，ry=4vvxx-8v(v2u)x

直接代入方程(3)验证即得.

命题2 如果(u,v)是方程(8)的解，则有函数关系(6)确定的函数(p,q,r)是下面(2+0)维方程的解.

(10)

在条件(1.10)下，(1.3)可以约化为

(11)

利用命题1和命题2我们很容易得到：

命题3 如果(u,v)是方程(8)和(9)的相容解，则有函数关系(6)确定的(p,q,r)是方程(11)的解.

3 结论

本文利用两个(2+1)维耦合mKP方程的Lax对，对位势施加约束，就约化为KN方程，并且证明了KN方程的相容解就是耦合mKP方程的解，这样就可以间接地得到耦合mKP方程的解.

[1]谷超豪等著.孤立子理论与应用[M].杭州:浙江科学技术出版社,1990:23-27.

[2]M.L.Wang ,J.Phys.Lett.A[J].1995,16(3):169-172.

[3]王烈衍.扰动非线性薛定谔方程的Painleve分析和精确孤立子解[J].宁波大学学报(理工版),1999,12(2)37-41.

[4] J.S.Zhang,Y.T.Wu and S.M.Li,Physics A[J]. 2003, 319(12):213-232.

[5]刘萍,Broer-Kaup系统的达布变换及其奇孤子解[J].数学物理学报,2006,26(7):999-1007.