复合材料单层飞轮转子模态分析
2014-08-22张兴蕾
张兴蕾
(枣庄学院 机电工程系,山东 枣庄 277160)
0 模态分析原理
实际工程中的弹性结构,可以离散化成有限质量、阻尼和弹性元件组成的N个自由度线性振动系统[1].结构动力方程为

(1)

当{Q}=0时,即结构不承受外载荷,若再将阻力忽略,则动力方程可写成:

(2)
方程(2)为系统的自由振动方程.对方程(1)两端作傅里叶变换得:(-ω2[M]+jω[C]+[K]{X(ω)})={δ(ω)}
(3)
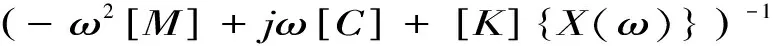
{X(ω)}=[H(ω)]{δ(ω)}
(4)
上式中 [H(ω)]为系统频率响应函数矩阵;[X(ω)]为响应{x(t)}的傅氏变换;
{δ(ω)}为激励{δ(t)}的傅氏变化.[H(ω)]也也称之为导纳矩阵,元素H1p(ω)的物理意义:当其它点上激励为零时,1点响应谱同p点激励谱的复数比,即
(5)
因为导纳矩阵具有对称性,所以只要通过提高测试获得导纳矩阵的一列或一行元素,就能确定整个导纳矩阵,便可以确定系统全部的动态特性了.在结构阻尼、小阻尼或比例阻尼存在的情况下,通过振型矩阵的正交特性,可以获得导纳矩阵与模态参数的关系式:
(6)
式中,(φ)i为第i阶振型,mi,ki,ci分别为第i阶质量、模态刚度、阻尼.通过运用实模态阻尼参数识别理论来进行模态参数的识别,就可以获得每阶的模态参数.弹性结构的振动本身具有连续性,位移{u}也是连续的,包括无限个自由度.在有限元离散化结束后,单元内的位移按照事先假定的位移形式来振动,节点位移差值可以表示该振动.此时,连续系统的振动就被离散化成有限个自由度系统的振动.如果全部节点的自由度为N个,那么式(6)就称之为N阶自由度系统的自由振动微分方程.根据自由振动的理论,N阶自由度系统的自由振动方程公式(6)应该存在N个固有频率ωk(k=1,2....N),ωk通过频率的行列式得出:
(7)
求解式(7),即可得出N个固有频率与振型,如果结构存在刚体位移,那么对应的模态为零频.针对一般的工程问题,只需要计算前6阶模态即可.对高速旋转的单层复合材料飞轮转子进行有预应力的模态分析[2],可以获得其振动的固有频率和振型,以此来评价材料的动力学特性,进而判断其是否发生共振情况,检验模态设计结果是否满足控制系统要求.
1 一阶固有频率理论计算
飞轮转子的第i阶固有频率fi对应的临界转速ωi为[3]:
ωi=60fir/min
(8)
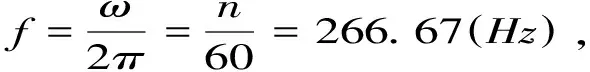
2 单层复合材料飞轮转子模态分析
对高速旋转的轮转子进行有限元模态分析,其模态的提取方法为分块兰索斯法,它具有求解精度高、计算速度快等优点,适合用于称特征值的求解问题.因为低阶模态对振动系统的影响较大,因此在进行结构的振动特性分析时一般提取前5—12阶即可满足要求,本文提取是飞轮转速为16000rpm的前6阶模态,模态的扩展阶数为6.其固有频率和固有振型,计算结果如表1及图1所示:
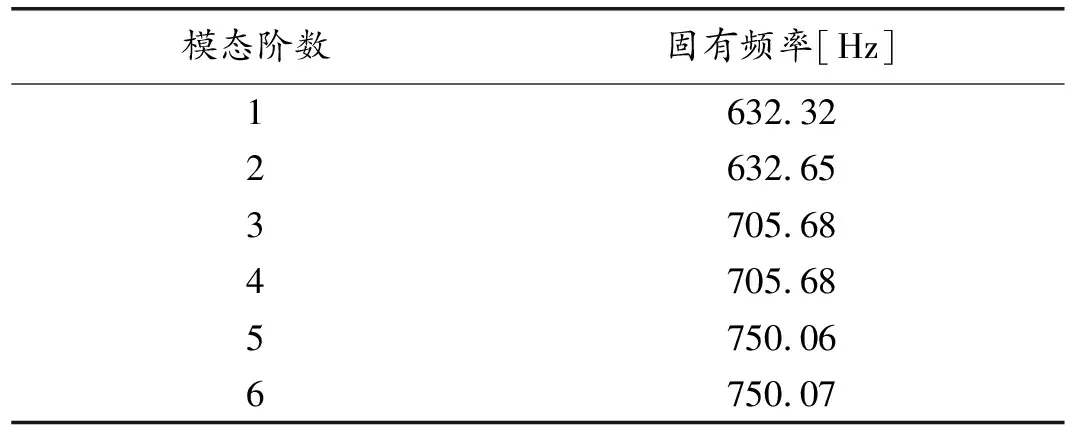
表1 飞轮转子的前六阶固有频率
储能飞轮转子的前6阶固有频率如表1所示,前6阶固有振型如图1所示,一阶固有频率为632.32Hz,明显远大于理论计算值266.67Hz,这说明飞轮转子从静止状态到16000rpm的加速阶段乃至以后的匀速旋转状态都不会产生共振现象.
3 结论
对高速旋转的复合材料飞轮转子进行固有频率分析,获得高速旋转飞轮转子的前6阶固有频率及固有振型,其中1阶固有频率为632.32Hz,明显远大于理论计算值266.67Hz,在飞轮转子的工作环节是不会引起共振的,满足控制系统要求,对预测高速旋转飞轮转子的损伤或破坏起到了理论应用和参考价值.
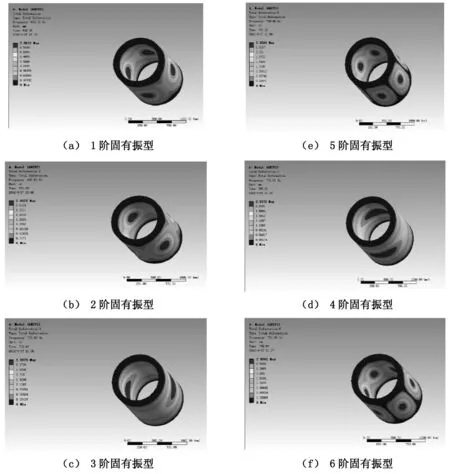
图1 飞轮转子前6阶固有振型
[1]孔繁鑫,黄勤,李光喜,等. 高储能飞轮转子动态特性及应力分析[J].机械设计与制造,2014,5:28-30.
[2]张兴蕾,李帅. 单层复合材料飞轮转子仿真计算分析[J].枣庄学院学报,2013,30(5):89-94.
[3]王庆五,左昉,胡仁喜.ANSYS10.0机械设计高级应用实例[M].北京:机械工业出版社,2006.
