分形求和法在工业生产中的应用研究

许丽华

(江苏联合职业技术学院 盐城机电分院 ，江苏 盐城 224005)

0 引言

通常我们在研究自然界中的各种现象时，发现它们大部分是无序的、不稳定的和随机的，不存在任何线性关系.但为了研究方便，习惯于将复杂的研究对象简化、抽象，建立起各种理想状态下的线性模型，从而将问题加以解决.虽然从数学角度上这种近似方法也可以解决一些较为简单的问题，但对于复杂一些的非线性系统和过程，用传统的数学工具根本无法描述[1].近年来，非线性科学领域研究中发展起来的分形学从纷繁复杂的系统本身入手，揭示非线性系统中有序与无序、确定性与随机性的统一.

分形理论借助相似性原理洞察隐藏于混乱现象中的精细结构，打破了传统的线性观，开拓了人们认识复杂现实世界的新思路和新途径，使人们能以全新的观念和手段来处理这些难题，透过扑朔迷离的无序的混沌现象和不规则的形态，探索和揭示隐藏在复杂现象背后的规律及本质联系[2].为人们从局部认识整体、从有限认识无限提供新的方法论，为不同的学科发现的规律提供了崭新的语言和定量的描述，为现代科学技术提供了新的思想方法.近 20 年来，分形理论在自然科学、社会科学及工业生产等许多领域中得到了广泛的应用，并逐步成为连结现代各学科的纬线.

1 分形模型和分形求和法

设分形模型

N(r)=Cr(D r>0

(1)

其中r表示特征尺度，C>0称为比例常数，D>0称为一般分维数，N(r)=N(≥r)表示尺度大于等于r的数目或和数.例如r可表示金品位，N(≥r)表示金品位大于等于r的样品数目或和数.分形分布可以应用于那些具有标度不变性的地质现象，而标度不变性则提供了应用分形分布的基础.

设研究数据{xi}，i=1，2，…，N.记

(2)

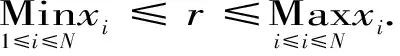
log[N(r)]= (Dlog(r) + log(C)

(3)

用最小二乘法求出斜率D的估计量，即为分维数；如果其散点大致分布在二段直线上时(即分二组的情形)，可采用分段拟合，有的界限点清楚，有的则不清楚.为了提高界限点确定的客观性，在二个区间用最小二乘法进行回归时用了最优化方法确定界限点.其基本思想是，找出合适的界限点ri0，使各区间拟合的直线与原始数据点之间的剩余平方和Ei(i=1，2)在两个区间的总和：

(4)

为最小.其中ri0是界限点，D1和D2分别为相应区间的斜率即分维数.为了检验回归方程的显著性，对每个回归方程都进行了相关系数检验及方差分析检验.该方法可以推广到三段直线以上的情况，即分三组以上的情形.

2 求和法在工业数据分析中的应用

我国是个资源大国，随着经济的发展和资源的开发利用，工业生产中产生的“三废”也在日愈增加，迫使我们一方面要减少对其的排放，一方面还要增加对其的综合利用[3].因此，如何通过对工业“三废”数据特征进行客观、有效地分析，建立科学合理的预测模型，进一步探讨工业“三废”的行为机制，成为需要解决的重大问题.分形求和法的提出，为解释复杂系统的动力学行为机制提供了有力的工具，从时间序列数据中研究复杂系统的分形特征，为准确反映系统的变化规律发挥着越来越重要的作用，其目前已经在化学、生物、地质、气象、水文等诸多领域得到了广泛的应用[4].笔者根据湖南省1993—2012年近20年的工业废气排放总量和工业“三废”综合利用产品产值数据，通过分析其分维数，研究其分形特征.表1和表2数据均来源于湖南省1994年—2013年统计年鉴.

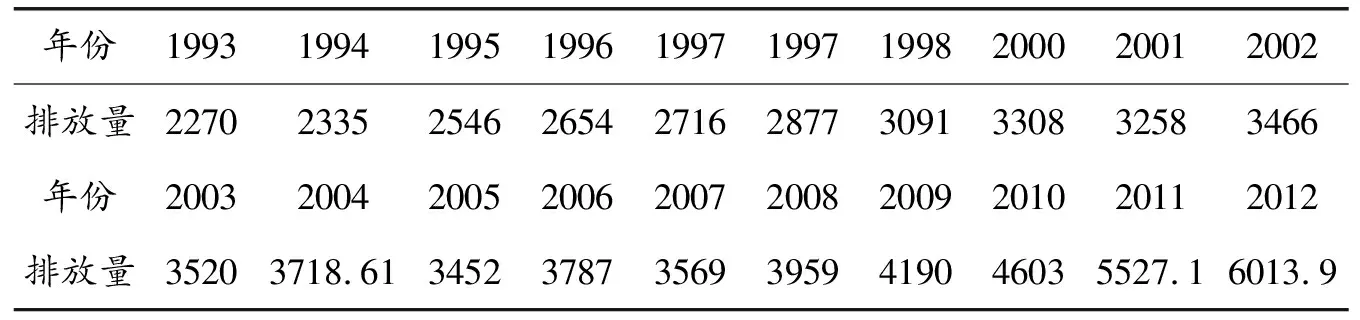
表1 工业废气排放总量(单位：亿标立方米)

表2 工业”三废”综合利用产品产值(单位：万元)

根据表1中1993年到2012年的工业废气排放量数据序列，我们选取相应的r值，保证2270≤ r ≤ 6013.9即可，所选取的r值和经计算所得的相对应的N(r)值见表3.同理我们可以根据表2中的数据序列选取相应的r值，保证19932≤ r ≤ 263513.6即可，所选取的r值和经计算所得的相对应的N(r)值见表4.

表3 工业废气排放总量的N(r)

表4 工业三废综合利用产品产值的N(r)

根据表1和表3中的数据序列{xi}，i=1，2，…，20.在lnN(r)-lnr坐标中投点，用最小二乘法拟合直线(见图1)，得到相应的工业废气排放总量的直线方程为：

LogN(r) = -2.424805535 Inr + 30.184593882270≤ r ≤ 6013.9

因而得到分维数 D = 2.42；同理根据表2和表4中的数据可以得到工业三废综合利用产品产值的直线方程：

LogN(r) =-0.1382929868 Inr + 15.8742920719932≤ r ≤ 80000

LogN(r) =-1.520647185 Inr + 31.4504393180000≤ r ≤263513.6

得到相应的分维数 D1 = 0.138；D2 = 1.52；界限点r0= 80000，它所对应的是2001年工业三废综合利用产品产值.图2为相应的lnN(r)-lnr图.以上方程均通过显著性检验.

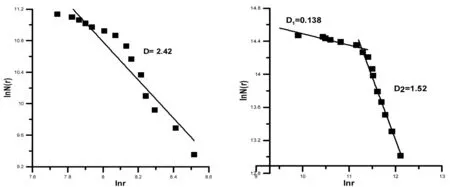
图1 lnN(r)-lnr图图2lnN(r)-lnr图

从图1我们可以得到分维数D=2.42，它反映了湖南省从1993年至2012年间工业废气排放总量的变化趋势.从总体上看，湖南省近20年里工业废气排放总量大致呈现增长的趋势，分维数的大小反映了工业废气排放总量增长的趋势大小.从图2我们可以得到分维数D1=0.138，D2=0.152，分界点r0=80000，它所对应的是2001年工业三废综合利用产品产值.可以看出，从总体上看，湖南省近20年里工业三废综合利用产品产值大致呈现增长的趋势，分界点r0所对应的年代产值都要比前8年的年代产值要大，而比后11年的年代产值要小.这2个分维数的大小反映了这二部分的变化趋势大小.其中分维数越大，表明变化趋势越大；分维数越小，表明变化趋势越小.

3 结论

基于分形模型，提出分形求和法，通过对湖南省的工业废气排放总量和工业三废综合利用产品产值数据进行分析，通过分维数的大小准确的反映了其变化趋势的大小.该方法与传统的概率图模型方法得到的结论一致，不仅适用于工业生产中的时间序列数据，而且还适用于农业生产数据、地质数据等[5]，具有普遍的意义.

[1]郭玉滨.关联规则挖掘算法研究[J]. 枣庄学院学报，2006，23(2)：70-73.

[2]董科强.分形理论和时间序列分析若干问题研究[D].北京：北京交通大学数学系,2011.

[3]丁俊,孙洪泉.优化分形维数计算方法[J].四川建筑科学研究,2011 ,25(5)：34-35.

[4]刘青,刘丽丽.江西省煤炭产业前后向关联分析[J].枣庄学院学报，2013,30(2)：49-54.

[5]朱叶红,朱道才.基于灰色关联方法的安徽产业协同分析[J].枣庄学院学报，2012,29(5)：57-63.