分形的推广、应用和某些基本问题

张一方

(云南大学 物理系，云南 昆明 650091)

0 分形和自相似性

分形(fractal)理论正式创立至今30多年，在这短短的期间，它已经取得了重大的理论进展，被广泛地应用于众多的领域，迎来了万紫千红的大好春光.“春色弥漫溢天地”，从天文到地学，从各种自然科学到众多的社会科学都掀起了一浪高过一浪的分形热.

分形是一种新兴的洞悉和思考自然界中复杂性和简单性统一的科学方法[1～4].自然分形具有自发性、深刻性和神秘性.微观世界和宏观世界分形的自相似性，包括独特性和差异性的失似性(dis-similarity)，是动力学系统中所有复杂的内部反馈关系的产物.

自相似性和分形的基本思想，应该说在中国或外国都是早已存在的.华夏最古老的经典《易经》就是基于相似性，对万物的归纳、分类.“仰则观象于天，俯则观法于地，……近取诸身，远取诸物，于是始作八卦，…… 以类万物之情.”人应当顺应自然，才能“与天相似故不违”.老子所言“治大国若烹小鲜”.中国哲学的阴阳、五行观都是应用类比性.佛教中更具有丰富的分形思想.唐代高僧，佛教天台宗创始人法藏(643-712年)就明确提出“一即一切”，“一切即一”.宋代禅宗临济宗高僧方会(992-1046年)在《古尊宿语录》中进一步阐述了“一即一切”的思想，认为“一尘才举，大地全收”，“于一毫端，现宝王刹”.禅宗高僧玄觉在《永嘉证道歌》中说：“一性圆通一切性，一法遍含一切法.一月普现一切水，一切水月一月摄”.程朱理学从理的角度也论述了天地万物间“理”存在的普遍性和“理”相似的分形性.《菜根谭》中“一勺水便具四海水味，世法不必尽尝；千江月总是一轮月光，心珠宜当自朗”，更以诗的语韵描述了自相似性.

古埃及人相信一个精子就是一个极小的形体完整的人.古希腊阿尔克莽认为人是小宇宙，它和大宇宙相似.柏拉图在《蒂迈欧篇》中类比大宇宙和人，甚至推演出宇宙的结构和人体生理的相似性.莱布尼兹在《单子论(Monadology)》中假设，每个单子是一个灵魂，一切单子反映整个宇宙.佛经中说：“一沙一世界，一叶一如来.”外国诗人W.Blake在《天真之兆》中回应为：“一沙见世界，一花窥天堂，手心握无限，须臾纳永恒.”但是中外先贤的这些卓越思想只是一些定性的方法和推测，而分形则是一种定量的科学方法.

1 分形的推广

非数学的、实际存在或应用的分形都只在一定范围，即标度不变性区域成立.为了超越这一区域，或突破整个系统只能有一个分维值的局限性，人们进行了一些探索.其中最著名的有多重分形(multifractal)[5-8]和广义维数(generalized dimension)等.

多重分形是为研究物理量或其它量的奇异分布而引入的基本概念.一般地说，一个非均匀分形需要通过无穷多个广义维数Dq(q>0)来表征.当q=0,1,2时，分别是最基本的分形维数、信息维数和关联维数.只有在均匀的情况下，这些维数都相等，变为通常的分形维数.

多重分形又称多标度分形，它在不同的标度或不同的方向具有不同的分维值.它描述一个具有标度特性的分形体，在生长过程中不同层次的特征.每一个不同的层次用不同的参量表示.这些不同的参量构成一个集合，亦可理解为某个物理量.这个量在分形体上的分布就反映为多重分形谱.为了在数学上获得定量描述，将研究对象分为都具有标度性的多个层次，或者线度不同的小区域，并用特征标度指数αi来表征，于是得到一个由不同的αi所组成的集合.由此可以研究一个正在演化中的结构.

多重分形理论把大尺度分为许多小尺度的方法，从分形体的部分出发研究其整体特征的思想，这与热力学中把系统分成许多宏观小而微观大的子系统，及由局部看整体的物理思想是一致的.因此，多重分形的描述可以转化为热力学的形式，这种类比是一种重要的研究方法.经比较发现αi相应于能量，标度指数谱f(αi)作为一个连续函数相应于熵，由此还可以引入相应于温度、自由能和配分函数等的量，从而了解产生谱的动力学.对此进行深入研究发现，多重分形热力学不仅能给出分形几何的若干定量结果和一系列公式，而且能把刻画混沌运动的几个重要参数，如Lyapunov指数、测度熵等统一起来.但这种热力学描述只是形式上的类比，它所揭示的仍然是分形的几何特征.

利用多重分形理论来分析的大多数问题源于非线性的动力学系统.在这些系统中，一个重要的问题是临界点的相变过程.在发生相变的临界点附近，标度指数将有一个突变，标度不变性不成立.并且，如果没有外界条件的限制，这类结构的演化将导致特征标度指数的不断增长.此外，多重分形理论中还利用子波变换方法探索标度指数的空间分布，以便研究结构的对称性和演化.

多重分形、随机多重分形虽然提出了不少处理方法，但理论的完善、数学的严格以及如何用这些理论来解决实际问题等仍需要深入探讨.

某些学者试图发展分形的基本概念.把最初是指在形态或结构上具有自相似性的分形发展为广义分形.即扩充和发展自相似性，使之包括信息、功能、时间等方面的相似性，而称具有这种意义更广的自相似性的客体为广义分形.它可以是几何客体，也可以是数理模型或社会系统等.除自相似分形外，还提出过自仿射分形、自反演分形、递归分形等新概念，用它们表征自然界中一些不规则的非线性特征，它们不一定具有明显的自相似性.

Mandelbrot把分维发展为负数维[7].这是平凡的，因为实数已经包括负数，K=r-D表示尺度r越大体积K越小；反之亦然.在粒子物理中如果K是能量，则它与粒子结构中尺度越小，能量、质量越大完全一致.而且如果取r-1为尺度，则分维仍为正数，二者等价.

1988年4月笔者提出把分维推广为复数维[9]

Dz=D+iT.

(1)

它在复平面D-T中变化时是一条曲线.结合相对论，如果假设虚轴表示时间，实轴表示分维，则复分维表示在不同时间的分维.所以，它可以描述分维随时间的变化.这是加上时间轴的Hausdorff空间.进一步，在相对论的任意四维矢量中，作为第四维的能量、密度、频度等都是虚数部分，因此可以用复分维描述分维随这些量的变化情况.用复分维可以表述云的分维随聚集程度和时间的不同而变化，粒子的分形模型[9,10]随关联强度不同而分维变化.脑电波、心电图、生物的生长、地震波、企业管理、股市行情等的分维如果变化，就可以应用复数维.反之，基于复数维，由分维的不同值又可以确定各种变化过程所处的不同状态.在某些方面，复分维可以和多重分形联系起来.在纯数学中，如果对某一几何图形引入一个分维，则假如该图形变化就相应于复数维.1993年3月新创刊的《分形》杂志第一期发表了B.J. West和X. Fan的论文《混沌，噪声和复数分维》[11]，他们结合幂定律的指标和调制周期也提出了复数维.1998年，D.Sornette在《物理报告(Phys.Rep.)》上发表了一长篇文章“离散标度不变性和复数维”.由此可知，复数分维一定具有广大的发展前途.笔者对此也进一步进行了探讨[12].

如果r是实数则

K=rDeiTlnr=rD[cos(Tlnr)+isin(Tlnr)].

(2)

复数维就相应于三角函数.这样基本初等函数及相应的任何公式都可以联系于分维和复数维.

同时，分形可以从空间推广到结构、功能、信息、能量、时间等方面的自相似性.这是近似具有全息律的一类系统.

如果相对论始终成立，则空间、时间与动量、能量等四矢对称.空间、时间具有的性质也应该可以推广到任意四矢.如分维、复维等动量已经应用于量子场论中，进而应该存在于自然界中.

笔者已经提出，把分维表示为D=n(整数维)+d(小数维)，则分维矩阵是一个通常的矩阵加一行(列)特殊的小数维.由此可以发展分维线性代数、分维数学分析和分维集合等.而且数学中目前的分维几何，可以发展为复维几何及一般的分维、复维等的代数、方程等各种数学，其中分析的维数可正可负就是统一微积分的算符演算.它们的基础还是分数、复数等个方程、矩阵等的分数、复数数学的表示方法[13,14].同时应该研究非欧几何等几何中的分维.相应地，分维、复维及其发展可以应用于力学、统计物理和电动力学中，并且应该有分维量子理论，它又可以应用在粒子物理中.此外，还能够得到分维相对论等[13,14].

这样，空间维数已经从实数维拓广到超实数维和复数维.同时，随着复数发展为超复数的四元数、八元数等，对应于相对论中时空间组成复数，时间可以相应发展为三维、七维形式等高维时间.高维时间在某方面的意义可能是同一时间投影在不同的相空间中，或同一时间投影在相同对象的不同方面.进一步，由高维时间可以完全类似地引入分维时间，如2.3维或0.7维时间.甚至发展出时间维数可变的复数分维时间.于是可以形成空间和时间完全对称的高维、分维、复数分维的时空理论[13,14].并且可以讨论分维、复维等的物理、化学、天文、地学、生物、经济、社会科学等等.

笔者讨论了时间和空间，以及时空与四矢的对称性.然后研究各种力场中时钟快慢与某些效应，并且探讨了时空的相对-绝对性和量子时空、时空的多样性及时空对称性的破缺[15].周期可以认为是一定时标下的时间自相似性，由此可以定义周期的分维.这联系于时间分维.假设时间维数是T(通常为1)维，则时间用高于T为量度时为0，低于T时为∞，相应于发散，等于T时为t是有限值.

分维是选择适当的测度；有精细结构，自相似是其特征；适当的不规则性；描述复杂性.多重分形是把奇点的奇异性分为不同层级的结果.导数应反映奇异性的变化.方法是重整化群和标度理论.标度不变性导致分维是常数；多重分形对应多重标度性.推广分维的自相似性是一种特殊的无穷嵌套的对称性.自相似的数学表示是标度不变性，即标度x变化时，函数f(x)形式不变，例如KNO、Dao标度等.它们都应有相应的分维.

分维在数学、物理中的各种发展应保持自相似性.满足幂指数法则都是分维.它可以是1)分维D的数域、环等的发展.2)几何、自相似性的发展.这又可以是嵌套型或平移型等的发展.进一步可以：1.发展分维概念，拓广领域和数学方法.2.推广应用范围.3.计算机模拟.分形不能用微积分，而应该用差分，可结合量子理论.分形、分维也是量子化的，应联系于离散数学、离散物理.

3 分形的某些应用

目前，分形已经广泛应用于凝聚模型、材料科学、流体力学、薄膜淀积、粒子物理、高分子化学、催化剂表面、网状结构等物理、化学方面，及天体的分布和大尺度结构、海岸线、地表、地震、分子生物学、细胞、蛋白质、分形生物学、癌等天文、地学和生物方面，并应用于血液循环系统、肺及呼吸系统、神经系统等人体的组织结构[1-4].

具体而言，用分形凝聚模型可以模拟天体、地震、粒子、生物、核及易经等的各种生成、演化过程，这对应于演化分形.象牙内有毛细管，所以作为钢琴键.由此可以决定其分维等，并可以决定各种生物材料，如牛骨、动物角等的分维，以此确定作为代用品的优劣.进而可以作为仿制塑料的定量指标.

笔者讨论过物理理论中一般的相似性方法及其与分形的关系[16]，粒子物理中的各种分形，其共同基础可能是高能统计模型和相关的推广的混沌模型[17,18].在引入天文学和宇宙论中具有不同层次分形的基础上，笔者把它推广到任意直线型的泛分形理论和一般化的分形天文学.由此讨论了大尺度的分形宇宙学和宇宙的多重分形模型.并且探讨了这些分形可能起源于不同层次的阶梯式结构和各种相似性[19].

多重产生等的间歇指数完全类似分维，

(3)

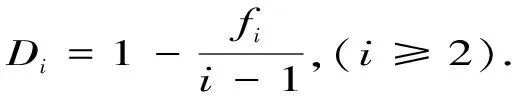
(4)

fp=(p-1)(1-Dp)=Dp+p-pDp-1,

(5)

其中Dp是通常的分维.如此定义则一定与p秩矩有关.由此可以利用相应的多重产生模型.

对高能重离子碰撞的间歇行为引入阶乘矩

∝(δy)-φi,

(6)

其形式类似分维.间隔宽度δy(0，间歇指数φi>0存在由动力学原因引起的涨落，δy足够小时φi=0则只有纯统计涨落.φi随入射能量(14.6，60，200AGeV)和末态相对论带电粒子平均多重数升高而下降，随靶核和射弹核质量增大而上升[20].φi随多重数增加而减少，所以分维D随多重数、能量增加而增大.

非线性的湍流、混沌中存在类似规律.间歇、反常子、半人马座事例可能存在共性，并且联系于1)相互作用相似.2)指数形式，可以化为分维.3)都是高能现象.

不同结构层次的自相似性，即它们的分维.分形是大、小尺度的对称，具有自相似性.因此可以用分形研究城市边界线、经济学、词频分布、管理、思维、音乐、文学、艺术等.更一般，科学社会学中都存在相似性和分形.对大或小系统，耗散结构和熵增都相同.少数服从多数的民主制和大小蜘蛛的独裁制都是自相似分形.

实际的分形具有一定的局域性.分维目前主要是测量结果，或由一定的几何等模型导出.社会科学中的分形具有模糊性.

分形应用于社会现象主要是随机分形，其生长模型等可以用于城镇的生成、舆论的产生等社会问题.分维及若干相应的社会问题可以分为相关的随机型和湍流混沌型等，例如用于分析物价涨落，如棉花价格的涨落.进一步，对任何随机过程都可以如此探讨.由此确定分维、大小尺度就可以预言股票、地震、气候等的变化.这类似易经.

易经、阴阳、五行和中国传统文化中具有丰富的相似性和分形.易经的基本结构就是一个太极生两仪(阴阳爻)、四象、八卦到六十四卦的倍周期分岔过程，由此最后达到混沌[21].这又联系于分形、分维，如果其等于2，则对应于布朗运动.国外更有人从时间波和分形时间预测灾难.这可能联系于地震周期.

文学中的典型性就是由局部反映整体的自相似性，就是一种分形.一篇短小精干的作品，栩栩如生描述的一个场景、人物常常可以概括芸芸众生中的诸多现象.鲁迅的《阿Q正传》是中国国民复杂性格的一面镜子.巴金的《家春秋》揭示了封建大家庭，乃至整个封建社会必然灭亡的结局.托尔斯泰的小说反映了五光十色的俄国社会.《辛德勒的名单》在短短的三个小时就用震憾人心的巨笔刻画了人性中善与恶的永恒主题.

4 分形中的某些基本问题

已知分维在双对数图中是一条直线.lnK=Dlnr，推广为lnK=Dlnr+C，则分维等于斜率D=tgα.因此分维在实数域中进一步的推广就是实函数曲线的切线函数.这应该是分维函数.它随时间、空间等变化，则D=D(x,y,z;t).类似广义分维是标度的函数.由此可以确定其在某些特定范围是否是直线，是否具有自相似性.它就和多重分形联系起来.在分维发展为复维后，还可以在复变函数中进行类似推广.然而D是x,y,z;t的函数就丧失了它的主要特点之一：简单、直观性.

数学上分形本身是无量纲的数.但物理上和在应用中分形和分维物体的量纲是非常奇异的.已知尺度的量纲是cm，D=2,3时K(面积、体积)的量纲是(cm)2和(cm)3.照此推理则D维分形物体K的量纲应该是(cm)D.更一般K=rD的量纲是r量纲的D次方.分维D不同则K的量纲是不同的cmD.并且在分形中随测量不同，或随过程演化，分维不断变化，量纲也随之变化.在复数维、多重分形等中更复杂，D渐变则相应物体量纲渐变，甚至是复数.当然，最简单的方法是假设分形无量纲，所以Mandelbrot称为分形几何[1]，但由此就无法与整数维的面积、体积统一.

在数学上，分形形式不仅直接相应于幂级数

y=xμ,

(7)

其中y是体积，x是尺度则D=μ.而且它可以推广相应于任何指数函数

y=abx=(ax)b,

(8)

则D=b；任何对数函数

y=clogax=c(lnx/lna),

(9)

以ay为体积，x为尺度则D=c或者

D=c-1=lnx/lnay,

(10)

则与指数函数的定义完全一致.

在几何图形中凡是直线，线性关系及可以化为此类者都联系于分形.类似地，波动性、周期性及与三角函数相关者都可以化为复数维.

与分形相关，笔者认为1)目前的重整化是对空间标度变化时的自相似性，应该可以推广到时间、能量、动量、系统及最一般的集合标度变化时的自相似性.这些都是大小标度.2)大小标度还可以推广到平移(如时空均匀)、旋转(各向同性)、反射(左右、前后对称)等.这已经是分形的推广了.3)这些标度等还可以推广到自仿射等各种几何.

‘tHooft维数重整化时，维数变小，则4阶矩阵(如γ5)也应该变成分数维矩阵及相应的分形等.这又联系于手征反常、维数反常等.

分形具有自相似性，分维不变也是一种标度无关性.标度无关性是标度改变时图形、函数等的不变性，应该对应重整化群或其推广.这是形象的定量结果.进一步分形可以发展到一般的对称性，结合一般群论，具有某个守恒量.此时的不变量就是分维.反之，只有分维改变，标度无关性和对称性破缺才会产生新相、新的性质.

由方程、系统等研究确定在什么条件下出现分形、吸引子等.后者具有自相似分形结构.

(11)

Gamma分布中

yΓ=Cxα-1e-βx.

(12)

β=0时y=Cxα-1；或α=1,y=C(e-x)β都可以认为是分形.相应的Pearson方程为

dy/dx=(D/x)y或dy/dx=-βy.

(13)

类似地，重整化方程也可以化简.

应该由非线性的Navier-Stokes方程导出湍流的分维.更一般，由基础的非线性，甚至简化为线性等方程可以导出相应的分数维；特别引入一定条件时.

物理自相似性都有一定层次.实际测量出的分维数一般不大，可能暗示构造复杂系统的模型时，并不需要用很多变量.关键只是序参量.

对一切在一定尺度、标度范围都成立的科学、真理都具有自相似性.同时，分形应该从几何推广到整个数学，如分形结合集合，则可以是分维D可变，及D不是整数.后者又联系于模糊数学.同时推广到物理、化学、生物、社会科学等.

5 宇观-微观分形、泛量子理论和展望

非标准分析(NSA)在表述上已经有自相似性[22].其应该是分形几何的解析表示.超实数b=St(b)+ε可能相应于无穷迭代的结果.NSA、超实数的无穷大可能又联系于重整化的发散.NSA中的分形主要是由一定假设求出分维数.

数学上最基本的是对大集合和小集合、大系统和子系统的自相似性.这应该结合分形、分维的定义和发展.分布和Cantor集D=0.6309等就是大集合类似小集合.

分形宇宙再推广则极大的宇宙相应于极小的粒子，星系对应原子核.可以由此确定分维数D，演化时又是复维.

由此联系于泛量子理论[23-27].它基于太阳系行星距离Titius-Bode定则新的表示形式

rn=an2,

(14)

由此可以发展完全类似Bohr原子模型的理论，并得到太阳系的量子常数[23,24]

H=(aGMΟ)1/2,

(15)

和相应的Schrodinger方程.许多卫星、太阳系外的恒星行星和银河系星团的10个伴星系都符合相同的公式(14).它又联系于量子宇宙论[23-25].进一步可以发展为仅仅量子常数不同而形式相似的泛量子理论，其数学基础是分形.某些宏观量子现象，如超导、超流、Bose-Einstein凝聚(BEC)、分数量子Hall效应也许就可以应用泛量子理论[25,26].进而可以发展到化学、生物等领域[25,27].

整数对应量子化，矩阵力学及矩阵，求和，及四维相对论、量子理论.分数对应量子化的发展，甚至连续性及积分，矩阵等的推广.可能一般的分维都可以结合模糊数学、模糊集合.分数对应模糊数学的隶属度.所有分维、复维理论都可以结合、类比高维理论，超对称理论等[28,29].

目前，分形理论的应用远远超过了理论的发展.分形在某些方面的数学严密性，它的解析基础和若干数学方法仍未完全确定.各种分形维数的计算方法和实验方法的建立、改进和完善，使理论简便，可操作性，仍是应用分形的科学家们关注的艰巨任务.

分形的发展方向之一是从几何学向动力学的飞跃.它利用分维概念，解析地处理非线性方程，进而获得能描述平均混沌过程的控制方程.其中分维摄动法就是利用分维概念解析处理非线性流体力学方程，而得出的一种通用方法.它可以推广应用于各种类型的非线性方程.

分形理论中动力系统的分形集是最活跃的研究领域之一.它包含奇异吸引子，Julia集、Fatou集和Mandelbrot集等.其中某些具体问题，例如从动力学特征推断几何结构，及其反问题由吸引子维数推断混沌动力学；含参量动力系统在混沌临界态或突变处的分形集维数，都有待于进一步研究.

在哲学领域，相似性是认识论和方法论的重要课题.分形是相似性和全息性的定量化理论[30].分形是基于复杂事物一经分解将会变简单的这样一种世界观.它将有助于融汇把整体不断分解的西方还原论思想和由部分反映全局的东方整体综合观.分形更深层的哲学蕴含仍在开掘之中.

更一般，分维几何应该发展为分维科学：1)具有不同层级的自相似性，这可能就是一切物质、科学、社会等中都存在不同层级的相似结构的基础和原因.这可以利用标度性、重整化群等数学方法；可能具有半群对称性.还必须结合模糊数学.自相似性是不严格的；可能一层层局部相似，但始与终也许相差极大.2)从分维空间推广到时间、能量、动量、个体数等空间、相空间.这些都有自相似性.3)观察得越近，发现的细节越多.这对应于局域、微观起伏、涨落.进一步，复维等几何应该发展为复维等科学.这些发展都将为当代科学的前沿——复杂性研究做出贡献.

美国著名物理学家J.A.Wheeler说：“可以相信，明天谁不能熟悉分形，谁就不能被认为是科学上的文化人.”分形作为一种新兴的交叉科学，作为一种可以应用于众多领域的新方法，作为一种理论和应用都正在蓬勃发展的新潮流，正在和必将产生巨大的深远影响.

[1]B.B.Mandelbrot. The Fractal Geometry of Nature[M]. New York: W.H.Freeman and Company. 1983.

[2]高安秀树著,沈步明,常子安译.分数维[M].北京：地震出版社.1989.

[3]李后强,程光钺.分形与分维[M].成都：四川教育出版社.1990.

[4]林鸿溢,李映雪.分形论[M].北京：北京理工大学出版社.1992.

[5]R.Benzi, G.Paladin, G.Parisi, et al. On the multifractal nature of fully developed turbulence and chaotic systems[J]. J.Phys. 1984, A17(18):3521-3531.

[6]L.Pietronero & A.P.Siebesma. Self-similarity of fluctuations in random multiplicative processes[J]. Phys.Rev.Lett. 1986, 57(9):1098-1101.

[7]B.B.Mandelbrot. Negative fractal dimensions and multifractals[J]. Physica. 1990,A163(1): 306- 315.

[8]杨展如.分形物理学[M].上海：上海科技教育出版社.1996.

[9]张一方.粒子的分形模型,复数维及其意义[J].大自然探索.1988,7,2:21-23.

[10]张一方.粒子物理和相对论的新探索[M].昆明:云南科技出版社.1989.138-143; 239-243. Phys.Abst.1990, V93, No.1371.

[11]B.J.West & X.Fan. Chaos, noise and complex fractal dimensions[J]. Fractals. 1993, 1(1):21-28.

[12]Yi-Fang Chang. New tree-field representations in graph theory, extension of Dirac extraction, differential test for series of positive terms, complex dimension and their applications[J]. Journal of Modern Mathematical Sciences. 2014,9(1):1-12.

[13]张一方.数学,物理中分维的发展和分维时空理论[J].大自然探索.1991,10,2:49-54.

[14]Yi-Fang Chang. Fractal relativity, generalized Noether’s theorem and new research on space-time[J]. Galilean Electrodynamics. 2010,21(6):112-116.

[15]张一方.时空某些基本特征的新探索与时空多样性[J].枣庄学院学报.2014,31(2):20-25.

[16]张一方,物理理论中的相似性方法和分形[J].益阳师专学报.1995,12(5):32-37.

[17]张一方,粒子物理中的各种分形及其可能的共同基础[J].云南大学学报.1995,17(4):317-321.

[18]Yi-Fang Chang. Higgs mechanism, mass formulas of hadrons, dark matter and fractal model of particle[J]. International Journal of Modern Theoretical Physics. 2014,3(1):1-18.

[19]张一方.天文学和宇宙论中的各种分形及其可能的起源[J].湖南城市学院学报.2006, 15(3): 44-47.

[20]EMU01协作组.高能重离子碰撞间歇行为的系统研究[J].高能物理与核物理.1991,15(2): 131-136.

[21]张一方.易学、西方科学思想和混沌[J].科学技术与辩证法.1993,10(3),46-49.

[22]A.罗宾逊著,申又棖,王世强,张锦文译.非标准分析[M].北京:科学出版社.1980.

[23]张一方.Titius-Bode定则的发展,天体量子理论和泛量子理论[J].云南大学学报.1993,15(4): 297-303.

[24]Yi-Fang Chang. Development of Titius-Bode law and the extensive quantum theory[J]. Physics Essays. 2002,15(2):133-137.

[25]张一方.泛量子理论的发展及其在生化和物理中的应用[J].吉首大学学报.2006.27(5): 34-38;48.

[26]Yi-Fang Chang. Nanophysics, macroscopic quantum phenomena and extensive quantum theory[J]. International Journal of Nano and Material Sciences. 2013,2(1):9-24.

[27]Yi-Fang Chang. Extensive quantum biology, applications of nonlinear biology and nonlinear mechanism of memory[J]. NeuroQuantology. 2012, 10(2):183-189.

[28]张一方.粒子物理中的超对称,超统一和高维复空间[J].云南大学学报.2003,25(1):37-40.

[29]Yi-Fang Chang. Higher dimensional complex space, supersymmetry and some unifications in particle physics[J]. Journal of Modern Mathematical Sciences. 2014,10(1):75-89.

[30]张一方.复数维,分维时空及其哲学意义[C].分形理论的哲学发轫.四川大学出版社.1993. 313-321.