基于RecurDyn的行星耦合机构动力学仿真

贾小平,樊石光,于魁龙,邢 旺

(装甲兵工程学院,北京 100072)

铰接车一般具有较高的越野和越障性能,如适应壕沟、陡坡、台阶等恶劣路面工况.由于其具有良好的路面通过性,目前正广泛应用于农业、勘探、森林消防、救援抢险、军事等领域.铰接车的合理转向是一个关键问题,它的实现方法有很多种,本方案采用行星耦合机构来进行研究.行星齿轮机构可单独应用为传动系中的差速器、功率分流或汇流机构和可用为减速器,或串联为传动系中的增速、减速环节.若干行星排加上一些可控制其元件的制动器、离合器等,则可组成行星变速机构.与固定轴齿轮机构相比,其主要特点有:能实现单自由度运动的固定轴齿轮机构所不能实现的二自由度速度分解和合成;多点啮合传递动力,属于机构内部的多流传动,体积小,重量轻;传动时径向力平衡,承载力强,结构紧凑[1].行星机构的灵活应用变化很多,已成为传动系许多新发展的基础.

1 方案介绍与仿真模型建立

1.1 结构原理

如图 1所示,该二自由度耦合机构由两个行星排连接而成,用于实现某 8×8轮式铰接车的灵活转向.动力通过电机由两侧太阳轮输入,行星排1的行星架与行星排2的齿圈相固连,行星排2的行星架与行星排 1的齿圈相固连,最后动力经由两侧行星架输出,通过机械连接和机械传动后将转速再传至两侧车轮,原理图见图 2.驾驶员通过调节两侧输入电机转速的大小和方向,便可以控制车辆转向半径的大小及转向方向,同时可以实现无极调速.

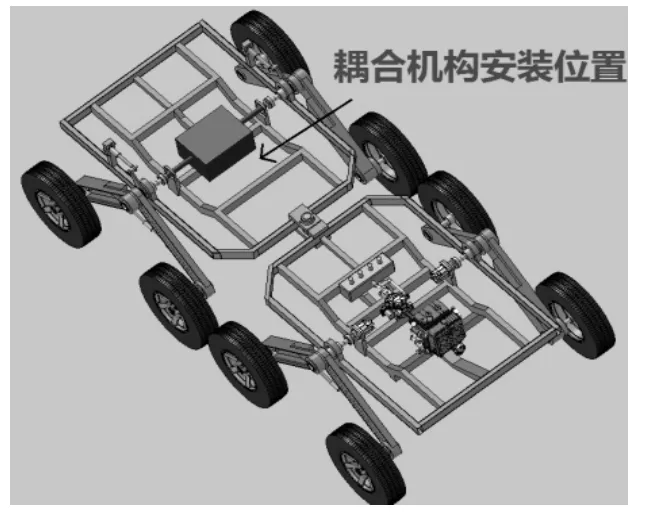
图1 8×8轮式铰接车及耦合机构安装位置示意图

图2 耦合机构动力传递及结构示意图

图3 耦合机构动力学模型

1.2 行星耦合机构模型建立

为对该耦合机构进行动力学仿真,基于RecurDyn/Gear工具包,建立其仿真模型(图 3).为便于分析,对两行星排中太阳轮、齿圈、行星轮、行星架分别采取同参数建模,行星排各齿轮参数见表1.

表1 行星排齿轮参数

另外各齿轮齿顶高系数为1,齿根高系数为1.25,模数为2mm,压力角为20°.质量、惯性矩、密度等属性及其它尺寸保持默认值[2].

2 基于Recurdyn的齿轮接触力理论介绍

根据Hertz接触理论,Lankarani提出了非线性弹簧阻尼模型[3],其公式为:

其中k为弹性系数,c为阻尼系数,m1、m2、m3分别是刚度、阻尼和凹痕指数,δ是穿透深度,δ˙是穿透深度的导数(本文中表示齿轮啮合点的相对速度).本文中k取 106N/mm,c取 2N·s/mm,摩擦系数取 0.03,m1、m2、m3分别取 1.3、1、0,δ取 1mm.接触力模型如图4所示.

图4 接触力计算模型

3 动力学仿真及结果分析

3.1 模型动力学仿真

对机构中组成元件施加约束,通过Joint来建立约束副,以此来限制不同实体间的相对运动,使系统中各部件组成一个有机整体.对机构中的啮合齿轮,通过建立齿轮接触对来实现正确啮合.各Joints及Contacts统计见表2.

表2 约束副及齿轮接触对统计

对太阳轮1输入157rad/s的驱动转速,太阳轮2输入转速为0rad/s,来表示电机传递的转速;对输出端的行星架1、2施加26000KN·mm的负载力矩,来模拟实际路面传递的负载[4].对机构进行运动学/动力学分析,设置仿真时间t=20s,步长 step=100;在获取力、力矩数据时为使结果更加准确,选取更多采样点,更改step为500.仿真结果转速和齿轮啮合力曲线见图5～8(对齿轮啮合力曲线图,行星轮与太阳轮、齿圈分别各有8个接触对,考虑到各对齿轮啮合力曲线比较接近,这里分别只取一对齿轮来进行受力研究).

图5 行星架1、2输出转速曲线图

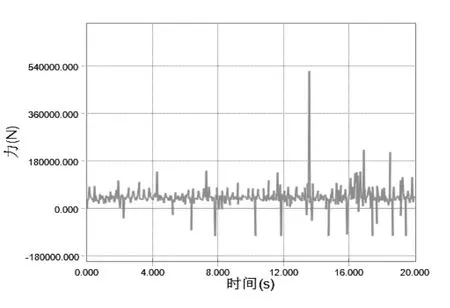
图6 太阳轮受行星轮啮合力曲线图

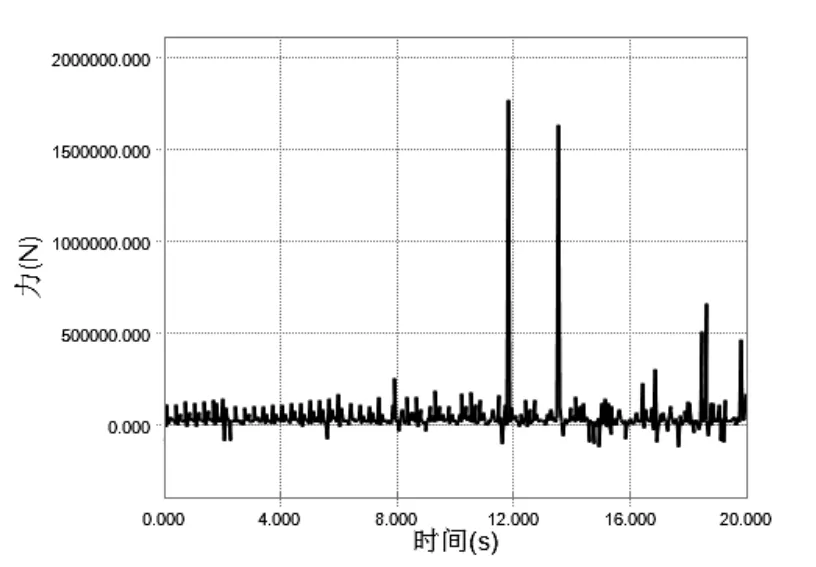
图7 齿圈受行星轮啮合力曲线图

图8 齿圈与太阳轮力矩曲线图

将数据从后处理界面中导出,去除尖点,对合理数据取平均值,可得仿真结果:

3.2 仿真结果分析

(a)转速分析

其中nti、nji、nqi(i=1,2)分别为太阳轮、行星架和齿圈的转速,k为行星排特性参数;由上述转速关系式,解得理论值

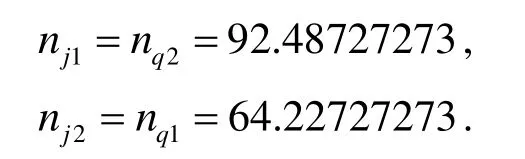
由曲线可知仿真值与理论值比较紊合,负号表示行星架与太阳轮转向相反[5].

(b)受力分析

其中Tt、Tq、Tj分别为太阳轮、行星架和齿圈所受力矩,Fbn为法向力,Ft为与分度圆相切的切向力,d为分度圆直径,n为行星轮个数.

由方程得理论解如下:齿圈所受切向力Ftxq1=Ftxq2= 4 1666.6667,太阳轮所受切向力Ftxt1=Ftxt2= 4 1666.6667,还有(齿圈)太阳轮所受法向力大小为Fbxq1=Fbxq2=Fbxt1=Fbxt2= 4 4340.7406;由仿真曲线知,仿真值与理论值比较存在一定误差,但在允许的范围内,仿真有效.另通过图可知,Tt= 7 934513.603,Tq= 1 7489500.560,其比值为2.204,接近2.25,符合比例关系.

4 含耦合机构的铰接车运动分析

对所研究铰接车,由于前后车体传动形式相似,此处只取后车为研究对象.当nt1=nt2=C时,nj1=nj2=C,模型车直线行驶,如图 9a;当nt1=C,nt2=−C时,nj1=−nj2,模型车原地转向,如图 9b;图9c为该8驱铰接车整体转向行驶示意图.

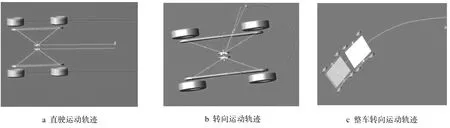
图9 铰接车运动轨迹

5 结论

本文通过RecurDyn建立了行星耦合机构的动力学仿真模型,通过仿真得到了太阳轮、齿圈的转速曲线和啮合力曲线.经过对比分析,仿真值与理论值比较紊合,仿真结果的比例关系也满足转速、转矩关系式.将该模型可用于铰接车的运动学仿真,从结果可知其运动轨迹符合理论分析.利用该模型,通过改变两侧太阳轮的输入转速可以达到车辆两侧所要求的速度,同时也可以为车辆提供驱动力,这为该铰接车后续的通过性仿真提供了条件.

[1] 闫清东,张连第,赵毓芹,等．坦克构造与设计[M]．北京:北京理工大学出版社,2007．

[2] 马星国,陆 扬,尤小梅．基于多柔体动力学技术的行星轮系多体动力学仿真分析[J].中国机械工程,2009,20(16):1956～1959

[3] 焦晓娟,张湝渭,彭斌彬.RecurDyn 多体系统优化仿真技术[M].北京:清华大学出版社,2010

[4] 陆 扬,马星国,舒启林．基于RecurDyn的行星轮系动力学仿真[J].沈阳理工大学学报,2008,27(4):76～79

[5] 孔凌嘉,王晓力.机械设计[M].北京:北京理工大学出版社,2009