一种基于蚁群算法的多物流配送中心选址策略

李文彬,王杨东,宋 亮

(1.湖南理工学院 信息与通信工程学院,湖南 岳阳 414006;2.湖南理工学院 复杂系统优化与控制湖南省普通高等学校重点实验室,湖南 岳阳 414006)

引言

物流配送中心是现代物流系统成本控制中的又一重要环节,合理的配送中心能够减少货物的运输成本,降低运营成本,促进生产和消费的协调与配合,保证物流系统的平衡发展.鉴于配送中心及其位置的重要作用,大量科研人员对这一问题展开过研究,提出了许多选址模型和选址算法[1,3],例如重心法、数值分析法、线性规划法以及传统启发式算法等等.但是这些算法都存在一些不足,重心法和数值分析法只能解决单一选址问题,对于多地址选择则无能为力.线性规划法和传统启发式算法虽然可以解决多目标问题,但是线性规划算法对目标函数的“线性”要求严格,传统启发式算法克服了线性算法的不足,但是对于大规模的实际问题求解还是很困难.

近年来,生物学进化理论[4]在计算机领域内影响越来越大,人们受到生物学进化机理的启发,研发出了一系列人工智能算法,如遗传算法,蚁群算法等.这些算法通常用来解决一些较为复杂的优化问题.本文提出一种基于蚁群觅食原理的匹配算法,将配送中心的选址过程映射成一种配送点和配送中心的匹配过程,利用蚁群系统中,蚂蚁利用信息素寻找最优解的机制,以物流配送总运输成本和配送中心建造成本最低为标准,结合蚂蚁对于路径选择的行为模式来定义配送点在选择配送中心时的转移概率和信息素的更新方式,把配送点和配送中心的匹配,以及配送中心和工厂的匹配作为一种解,从而确定配送中心的位置、数目和规模等信息.

1 蚁群算法基本原理

蚁群算法的本质是利用信息素作为引导,同时又更新信息素的一个正反馈过程.由于是正反馈,因此可以使得问题的解向着全局最优的方向不断进化,最终能有效的获得相对较优的解,解决全局最优化的问题.下面简单介绍一下基于路径寻优的蚁群算法[2].

这里以经典的最短路径问题来说明基于路径寻优的蚁群算法的基本原理.假设有 m只蚂蚁,目标是找到从A到B的最短路径,m只蚂蚁起始位置都在A上.刚开始时候,整个地图上信息素浓度是一样高的,设 τij( t )为 t时刻路径(i,j)上的信息素浓度.那么每只蚂蚁都根据当前位置上所能触到的道路上的信息素按概率选择下一步将要前往的点.其中第k只蚂蚁在t时刻从i走到j的概率为

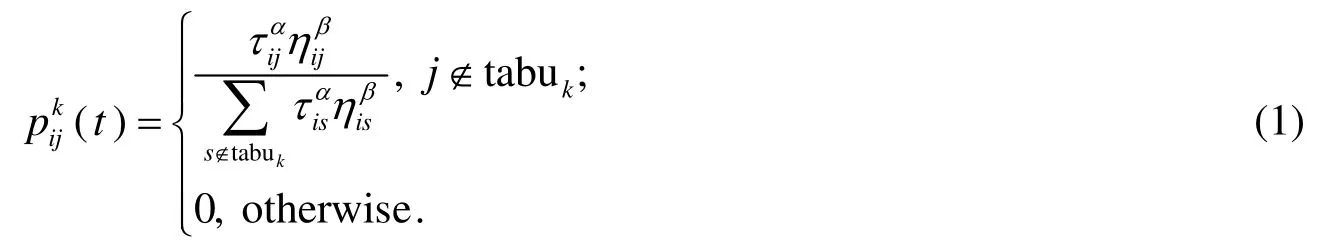
其中ηij表示蚂蚁从点i选择到j去的启发因子,α表示信息素对当前选择的影响程度,β表示启发因子对当前选择的影响程度,它们都是一个常数,tabuk表示第k只蚂蚁走过的点的列表.

设dij表示从i到j的距离,那么ηij的计算可以表示为:

如果 (i,j)的距离dij越大,那么蚂蚁对走这条路的期望就越小.

当蚂蚁从A走到B,便得到一个解,接下来更新蚂蚁走过的路径上的信息素:

其中Δτij表示道路(i,j)上的信息素增量,ρ表示信息素的挥发速率,通常取值在(0,1)之间.如果某一条路径上太长时间没有蚂蚁经过的话,那么它上面的信息素将挥发接近于0.相反经常有蚂蚁走动的道路,信息素浓度会越来越高.

可见基于路径寻优的蚁群算法是利用m只蚂蚁间的信息交流与相互协作,也就是说,每只蚂蚁在自己行走的路上留下信息素,后来的蚂蚁根据前进道路上信息素量的多少选择前进方向,在经过一个长的过程后,在较短路径上蚂蚁留下的信息素量将变得更多,最终找到最短路径.

2 多物流配送中心模型的建立

物流系统中的多物流配送中心选址问题,本质上其实是一个多目标的最优化问题.从现代物流发展的趋势看,多物流配送中心的研究具有长远意义.因此在本文中以对多物流配送中心选址为目标,以系统花费最小为标准,建立模型.物流配送总成本包括配送运营成本(含配送中心到配送点的运输成本和工厂到配送中心运输成本)和配送中心建造成本.

配送中心选址问题描述为在m个配送点中选则p个配送点作为配送中心,以合理的方案为每个配送中心指定配送点,为这m个配送点配送物品,使得在选出点建立的配送中心在满足配送需求的前提下,成本(包括建造成本和运营成本)最低.

设第i个配送点的坐标为( Xi,Yi),需求量为Ai,如果将它建成配送中心费用为Bi.工厂的坐标为(Zx,Zy).假设有配送点j需要通过配送中心i来运送货物,并设 Di表示工厂到配送点i的距离、Sij表示配送点i到配送点 j的距离.

那么此时费用为:

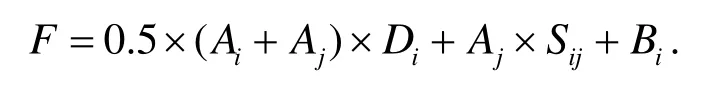
假设配送点到配送点运费为1,工厂到配送中心运费为0.5.

多物流配送中心选址的目标就是在这m个配送点中选出一些作为配送中心,并且为这些配送中心指定一些配送点,使得所有费用最低.

3 多物流配送中心选址算法

3.1 算法思路

算法的设计思路主要源自于基于路径寻优的蚁群算法和基于聚类的蚁群算法,让每个蚂蚁对每一个配送点分别进行一次匹配,当所有配送点都进行完了一次匹配之后,便会得到一个解,同时,蚂蚁为它的这个解留下信息素,用以引导后来的蚂蚁.新增信息素的值为1/tatolcost,所以,越好的方案留下的信息素浓度会越大,也会吸引越来越多的蚂蚁来,从而留下更多的信息素,这样不断的进行正反馈,从而将最终解不断逼近并最终确定,这和蚂蚁觅食时候寻找最短路径时的原理是一样的:利用信息素进行正反馈.

3.2 算法流程

Step1 维护信息素表τij,τij表示第t只蚂蚁在配送点i选择和配送点j进行匹配时的信息素.设有M只蚂蚁,初始化蚁群算法中的几个关键参数α、β和ρ,本文对α、β和ρ取值分别是1.3、1.0和0.95,并初始化能见函数:

其中dij表示配送点i和配送点j的距离加上将配送点j建设成配送中心的花费.请特别注意,还要加上花费.ηij表示i和j匹配为一对,并且将j建设成配送中心的期望程度.

Step2 设置禁忌匹配表tabuk(t),用于记录第k只蚂蚁在第t个配送点上不允许的匹配点.

Step3 蚂蚁以每个配送点为起点 (i = 0,1,2,…),在允许匹配的配送点中按概率将配送点i和配送点j匹配为一对,并将配送点j建设成一个配送中心.其中概率为:

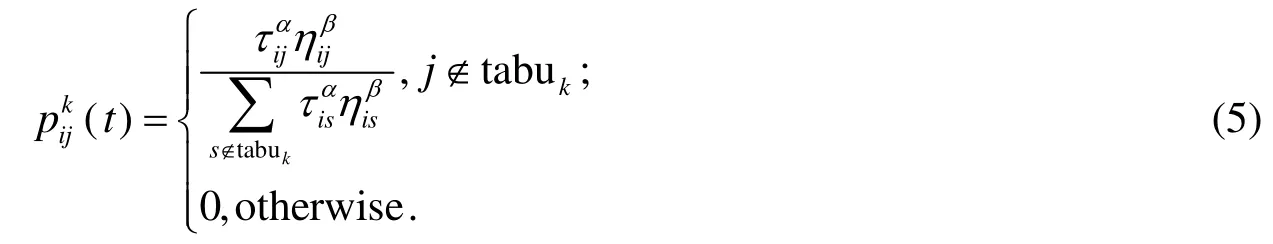
其中Ek表示第k只蚂蚁的方案的总花费,若Ek为0,则为0.

Step5 若M只蚂蚁都完成了一次循环,则转向步骤Step6 ,否则转向步骤Step2 .

Step6 更新信息素,

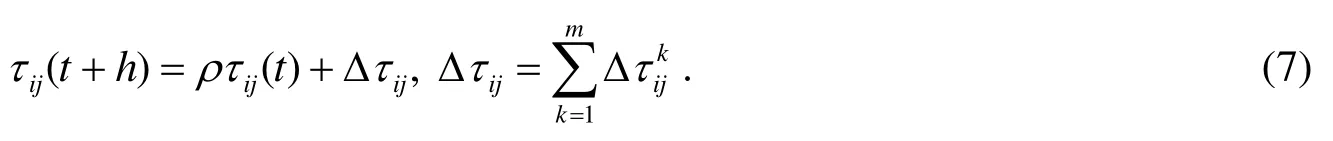
并重新回到步骤Step1 ,直到完成了一定次数的迭代.

4 算法仿真

根据上述算法描述设计实验.

实验一的数据如表1所示:

表1 配送网络的配送点情况

结果如图1,很理想.事实上,我们直观的就可以得到与实验结果相同的答案,其中1、2、5、6为配送点,3、4为选定的配送中心.

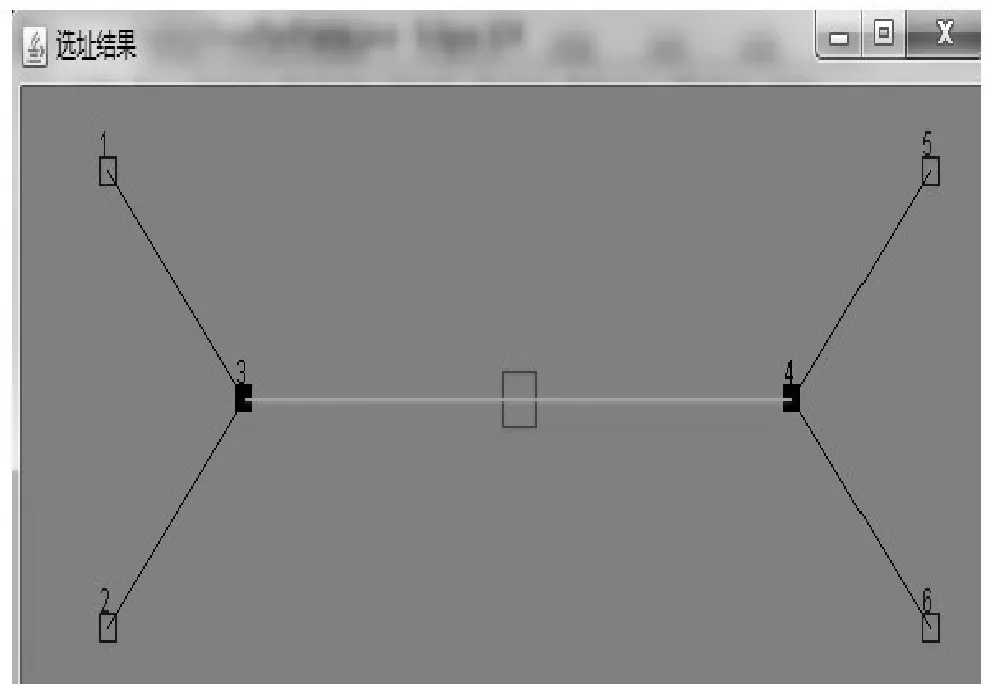
图1 实验一结果

为了确定中心建设成本与中心个数的关系,我们将建设成本提高至30,进行实验二,实验数据见表2:

表2 配送网络的配送点情况

仿真结果如图2所示,此时因为配送中心的建设成本增加,配送中心由实验一中的两个,缩减为了一个,配送中心只剩下3,其余的都是配送点.显然,实验结果和实际情况很吻合.

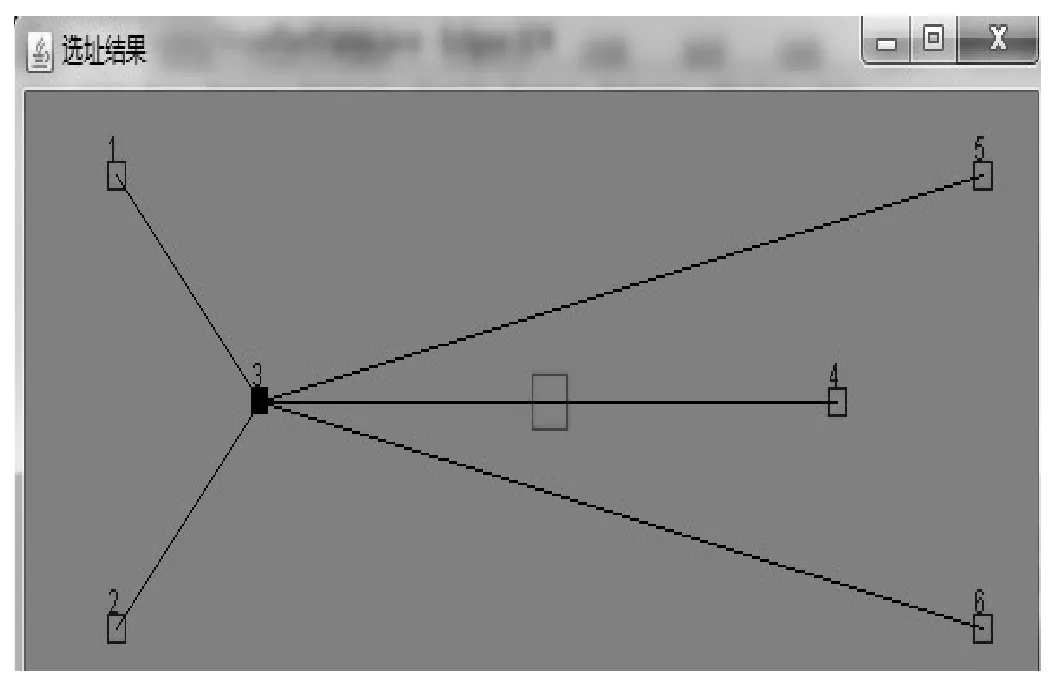
图2 实验二结果

为了进一步验证算法的正确性和灵活性,设计实验三进行实验,数据见表3:

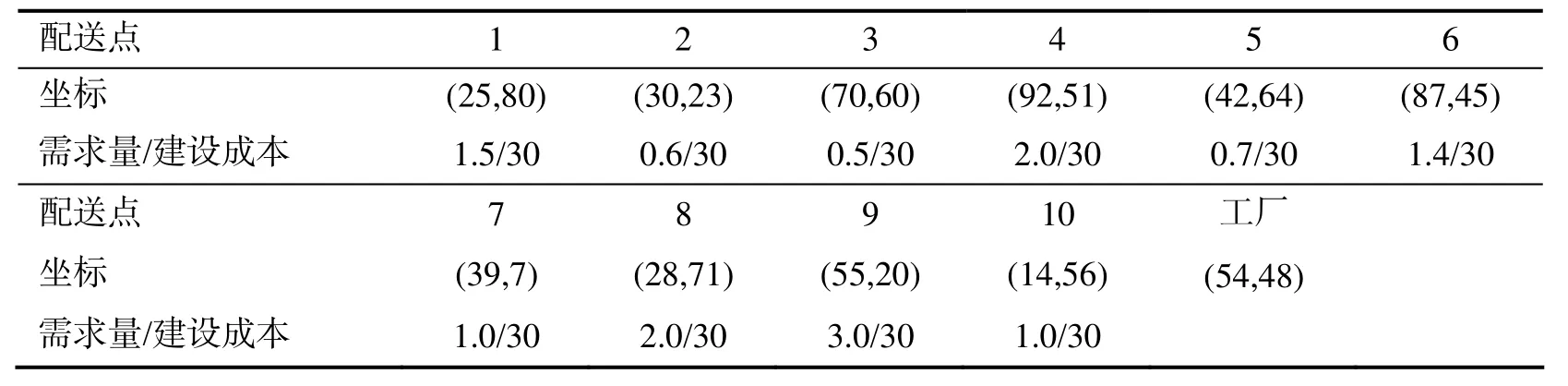
表3 配送网络的配送点情况

实验三中,设计点由原来的6个增加为10个,且每个配送点的需求量是不一致的,这是符合现实物流配送情况的.实验结果表明,此时的最优策略是,建立4个配送中心,为点4、5、8和9.结果如图3所示,其中配送中心4个,配送中心5负责配送点3和自己,配送中心4负责配送点6和自己,配送中心8负责配送点1、10和自己,配送中心9负责配送点2、7和自己.实验的结果符合预期.

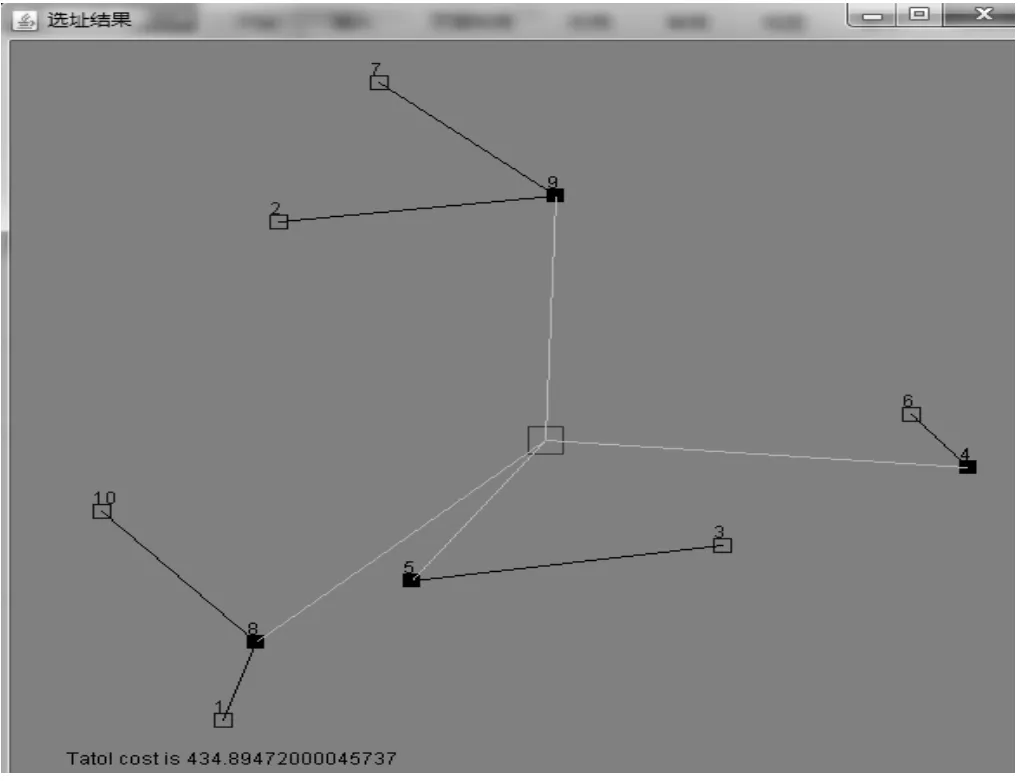
图3 实验三结果

在设计的三个仿真实验的过程中,算法规定工厂只能向配送中心运送货物.经过以上三个仿真实验,可以证明算法的模型是正确的,算法不仅确定了配送中心的位置、数量,同时还将与配送中心相关的配送点信息也求出来了.该算法具有很强的灵活性,例如将来可能需要考虑建设中心的管理成本,那么只需要对能见函数ijη以及信息素增量做出相应调整即可,无需改变整体算法架构,能够适应于现今多样的物流配送模型.

5 结论

物流配送中心选址是整个物流系统的关键环节,本文算法将物流配送中心的选址过程映射成一个特殊的匹配过程,以物流配送总成本最低为匹配原则,结合蚂蚁的觅食原理,将蚁群算法的精华运用到物流配送中心选址问题.由于蚁群算法本身所具有的鲁棒性和较高的计算效率,适合进行并行计算,对于解决大规模、复杂的物流配送网络具有很大的实际价值.而且该算法具有很强的灵活性,只需要根据不同的物流模型修相应的信息素更新函数,就能适用于现今多样的物流配送问题.

[1] 周根贵,沈雁飞.基于时间满意度的物流配送中心选址问题研究[J].浙江工业大学学报,2008,36(4)

[2] Deneubourg JL,Gross S,Franks N.The dynamics of collective sorting robot-like ants and ant-like robots[A].Proceedings of the 1st Conference on Simulation of Adaptive Behavior[C].1990:356～363

[3] 田立新,崔晓红,唐焕超.均差排序法在配送中心选址中的应用[J].江苏大学学报(自然科学版),2009,30(5)

[4] 吴 坚,史忠科.基于遗传算法的配送中心选址问题[J].华南理工大学学报(自然科学版),2004,32(6)

[5] Arhur E.Carter,Cliff T.Ragsdale.A new approach to solving the multiple traveling salesperson problem using genetic algorithms[J].European Journal of Operational Research,2005,(167)

[6] 董 亮.物流配送中心选址问题综述[J].科技信息,2013(7)

[7] 隋崴崴,宋现允,付 蕾.物流配送中心选址数学模型和算法问题研究[J].物流技术,2013,32(11)

[8] 汤希峰,毛海军,李旭宏.物流配送中心选址的多目标优化模型[J].东南大学学报(自然科学版),2009,39 (2)