重正化群方法分析政策对经济全面起动的影响
2014-08-17袁碧玉
袁碧玉
(成都信息工程学院,四川成都610103)
0 引言
地方(区域)经济的全面起动,国家或地方政策对其起着非常重要的作用。国家或地方的有利政策,能非常有效地为该地方或区域经济吸引投资、招纳人才,从而利于地方经济的全面起动。例如我国的深圳特区就是一个受国家经济特区政策影响经济全面起动的典范例子。
人们都知道,国家或地方政策对某地方经济全面起动起重要作用,但如何定量地描述、分析这种影响大小,如何评价不同政策的影响程度,目前基本上没有人进行过研究,更没有建立模型进行定量分析、评价。另外,还存在大量的类似社会、经济现象,可见本文研究具有重要的理论与实际意义。
1 重正化群理论
重正化群[1-3]方法是在量子场论中提出来的,应用于临界现象的研究,重正化群在不动点附近的性质决定了体系的临界行为。重正化群的目的是在观测中改变尺度时定量地获取物理量的变化。例如,把在某种尺度下所测得的物理量记为p,把在比这个尺度大两倍的尺度下测得的物理量记为p',利用适当的尺度变换f2,可以把p'和原来的p 的关系表示为:

其中f 的下标2 表示两倍的尺度变化。如果把观测的尺度再放大两倍,那么下列关系式成立:
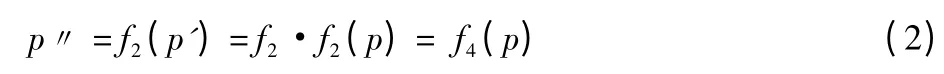
如果把这个公式变成一般化的关系式,那么就得知变换f具有下列性质:

其中:1 表示恒等变换。变换f 一般不具有逆变换f-1。
重正化群的一个重要定理是稳定不动点存在定理成立,即如果极限:

则有:

2 政策对地方(区域)经济影响率推导
把地方(区域)范围按地理位置分成若干个小块(或小区域),每个小块经济已全面起动,定义该小块形成一个“空穴”,如果整个经济区域“空穴”贯通,则整个地方(区域)经济已经全面起动。按照前面定义假想模型,组成地方(区域)经济带分布为规则排列如图1(a)所示,若以它们的形心代表每个小区域在大区域内的位置,则所有相邻的小区域形成的连线将构成二维的三角形点阵。现进行重正化群变化,其操作过程如下:
1)作一个kandanoff 变换,显然可取一个三角形点阵作为一个二级元胞,如图1(b)所示。
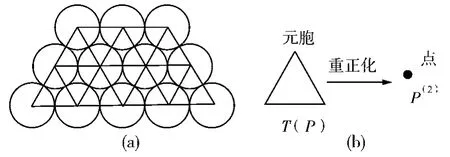
图1 三角形格点重正化变换
2)规定元胞的“导通”方向,根据“空穴”集团的定义,显然与方向无关,一个元胞中只要有两个(及以上)“空穴”形成就可定义元胞处于“空穴”贯通的导通态了。这样元胞的“空穴”贯通态可由单个小区域形成“空穴”的状态组成确定下来。
3)计算元胞的“空穴”贯通概率。已知在不考虑上级国家或地方政策影响的情况时,每个小区域形成“空穴”的概率为P,则可根据以上规定,一个元胞由三个小区域的各种形态组合可形成8 种组态,从中可找出4 种“空穴”贯通元胞的组态,这样可写出二级元胞“空穴”贯通的概率P(2):
同理对于高级元胞均有:

式(7)、(8)为不考虑政策对地方(区域)经济影响时的重正化群方程。
4)确定考虑政策影响时的重正化群方程。已知政策对地方(区域)经济的影响率为h,则对地方(或区域)带内经济全面起动的条件中还需要加上国家或地方政策对其影响的前提,而地方经济不受政策影响的概率则为(1 -h),所以地方或小区域经济起动的概率为P(1 -h)。同理对于元胞而言,经济起动的概率中也必须加上政策对其影响的条件。据此改写(1)式,并把不动点假定为P*,则有下式成立:
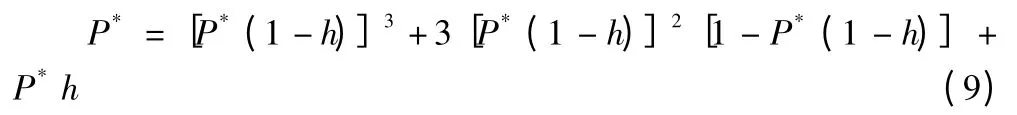
式(9)即为考虑了政策对地方经济全面起动影响的重正化群方程。
5)求解重正化变换的不动点。重正化群方法的一个重要步骤是寻找在重正化变化下的不动点,即对应于的点。可查曲线的交点,这样即得到不动点。需要根据Jacobi 矩阵特征值λ 的模来判断它们是稳定的还是不稳定的,只有∣λ ∣>1 对应的是不稳定不动点[4],而不稳定不动点才对应于临界点。
3 模型应用
下面举一例子,说明模型的应用。首先将确定的h 值代入式(9),则(9)式成为只有未知量P*的方程,求解即可得P*的值。如取h=0.1,代入(9)式为:
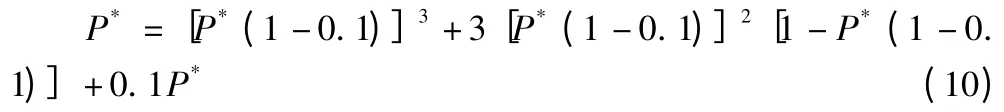
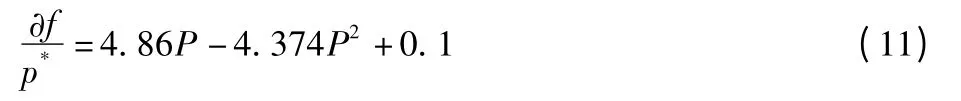
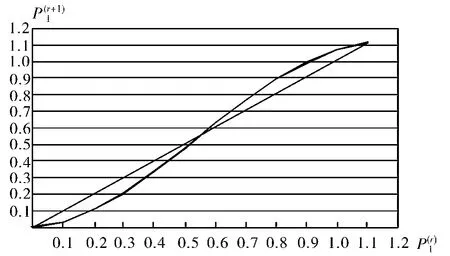
图2 重正化群关系曲线
只有 P=0.556,∣ λ ∣ =1.45 >1,故地方经济全面起动的概率是P=0.556。表1 给出了不同h 值,地方经济全面起动的概率。

表1 经济全面起动阈值PC 随h 变化表
由表 1 可见,PC值随 h 的增加而增大,当 h =0.5 时,地方或区域经济全面起动阈值为PC=1。
4 结语
有利的政策对地方或区域经济、社会起重要的影响作用,但如何定量地描述、分析这种影响大小及评价政策的影响程度,目前没有人进行过研究。本文以政策对经济全面起动为例,推导出了影响分析模型,结果可为大量的类似社会、经济等现象分析提供一种有效地定量分析手段。同时该模型兼顾了小区域经济全面起动对其他区域的长程相关作用,非常符合实际情况。另外,应用该模型还可分析多级政策对地方经济、社会现象的影响。
[1]赵松年. 非线性科学—它的内容、方法和意义[M]. 北京:科学出版社,1993.
[2]张济忠. 分形[M]. 北京:清华大学出版社,1995.
[3]周硕愚. 系统科学导引[M]. 北京:地震出版社,1988.
[4]姚令侃. 非线性科学探索推移质运动复杂性的研究[D]. 成都:四川大学,1996.
