基于Monte-Carlo的滑坡失稳概率计算研究

，， ，

(1.四川省地质矿产勘查开发局202地质队，四川 宜宾 644002； 2.成都理工大学 a.地质灾害防治与地质环境保护国家重点实验室；b. 环境与土木工程学院，成都 610059)

1 研究背景

对于滑坡的稳定性评价，最常用的是定值分析法。这是建立在确定性概念之上的。但在实际情况下，岩土体的物理力学参数(如摩擦因数、黏聚力、重度等)、孔隙水压力、外荷载是复杂多变的、随机的和相关的[1]。传统观念认为当稳定性系数Fs>1时滑坡处于稳定状态，Fs<1时滑坡可能失稳，这种跳跃性的判断标准也不合理[2]。同时对滑坡的失稳概率也不能确定，所以在对于滑坡的稳定性评价时，应加入滑坡的失稳概率计算才显得更为合理。

传统的滑坡失稳概率计算，通常把影响滑坡稳定性因素作为随机变量，认为岩土参数c和φ服从正态分布[2-8]，但在实际利用Monte-Carlo计算滑坡失稳概率过程中，土性参数概率分布类型的不同将影响可靠度指标的计算结果，严春风等[9]通过研究发现，当随机变量c和φ假设为不同分布形式时，结果的计算误差可达20%～30%。岩土参数的概率分布类型可分为5大类[10]：即Bernoulli分布系列、Poisson分布系列、极值分布系列、中心极限分布系列和用于统计分析的分布系列。不同的分布类型对滑坡的失稳概率计算有相当大的影响。且张继周和缪林昌[10]研究发现在实际应用中，中心极限分布系列对其描述较为合理，当变异系数<30%且偏度系数<0.025时，选择正态分布，反之，选择对数正态分布。因此在实际对滑坡失稳概率计算过程中，应首先考虑岩土参数c和φ值符合何种概率分布，再基于蒙特卡洛(Monte-Carlo)法进行滑坡失稳概率计算。

2 Monte-Carlo基本原理

目前滑坡失稳概率计算常用方法主要有一次二阶矩阵法[11]、概率矩点估计法(又称Rosen-blueth法)[12]、蒙特卡洛(Monte-Carlo)随机模拟法[13]等。由于蒙特卡洛法受问题条件的限制较小，收敛性与极限状态方程的非线性和变量分布的非正态性无关,适用性强,而且实力简单，易于编制计算程序，因而其应用越来越广泛[14]。

蒙特卡洛法，是用数值模拟来解决随机变量有关的实际工程问题的一种常用方法。对事件发生的概率可以通过大量实验所得频率来估算。当选取样本数量足够多时，实际发生的频率可等同为概率。蒙特卡洛法就是基于对随机变量大量抽样，然后将其代入其功能函数，判断其是否失效，从而得出失效概率。如对于滑坡的稳定性系数，其受力状态、土体结构的函数可表示为

Fs=f(σ,τ,h,w,p…)。

(1)

式中：σ为正应力条件；τ为剪应力条件；h为地形条件；w为地下水条件；p为外荷载条件。这些参数均是随机变量，大部分服从正态分布或对数正态分布。

其功能函数可表示为

Z=Fs-1 ,

(2)

则失效概率即滑坡破坏概率可表示为

(3)

式中f(Fs)为Fs的概率密度函数。

在实际抽样计算过程中，可用下式方法计算其破坏概率：

Fs=N/M。

(4)

式中：M为模拟的总次数；N为出现Fs<1的次数。

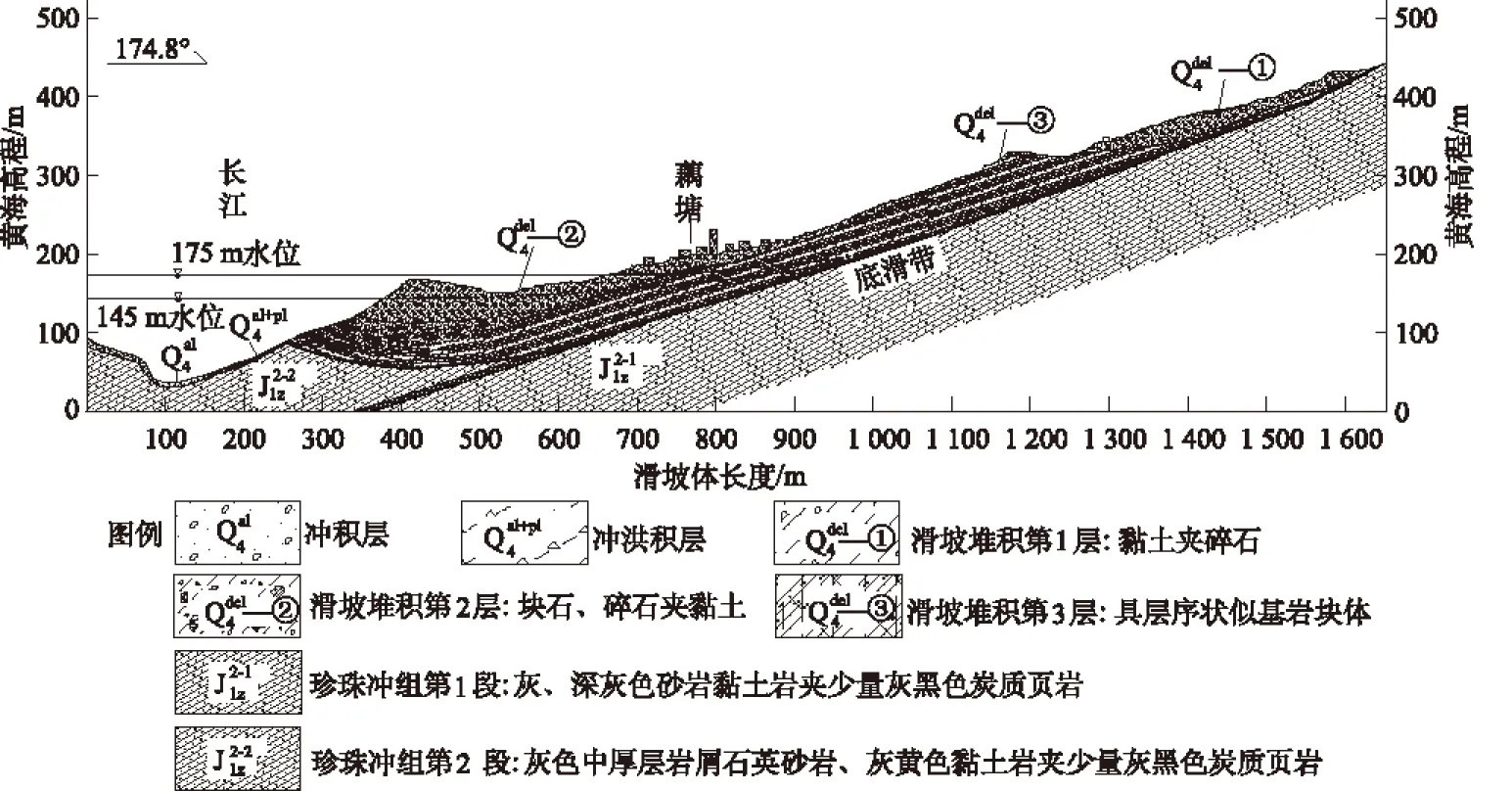
图1 藕塘滑坡地质剖面图

3 工程实例

3.1 滑坡概况

藕塘滑坡位于奉节县长江南岸，系安坪乡新集镇所在地。安坪乡行政区划隶属重庆市奉节县，位于奉节县城上游约15 km。

滑体前缘高程95～102 m，后缘高程475 m，滑体南北向(从前缘到后缘)长约1 500 m，东西宽830～1 170 m，面积133×104m2，一般厚40～70 m，最厚为114 m，体积约6 380×104m3。第四系堆积物按其成因可分为：①冲积层(Q4al)，厚一般1～5 m；②冲、洪积层(Q4al+pl)，厚1～5 m；③滑坡堆积层(Q4del)。其地质剖面图见图1。

区内出露地层为侏罗系中统新田沟组(J2x)、侏罗系下统珍珠冲组(J1z)、自流井组(J1zl)和三叠系上统须家河组(T3xj)。

3.2 滑坡参数选取

根据藕塘滑坡多组钻孔取样进行室内试验和现场试验取得滑带土岩土力学参数c和φ值，并计算其均值、标准差、变异系数、偏度系数，见表1。

表1 滑带土物理参数

3.3 考虑变异系数和偏度系数计算滑坡失稳概率

对于非标准正态分布，可采用标准正态分布N(0,1)的随机变量x′经过线性转换得到：

X=μ+σx′。

(5)

式中：x′为标准正态分布随机变量；μ和σ分别为所求非标准正态分布随机变量X的均值和标准差。

本文采用Box和Muller提出的变换法[11]，取2个独立的[0,1]区间均匀随机数u1和u2，利用二元函数转换，再由式(5)得到正态分布N(0,1)的随机变量。

对数正态分布和正态分布有确定的转换关系，如果随机变量Y服从平均值μ和方差σ2的正态分布，可通过公式X=eY，则X服从对数正态分布。

根据张继周和缪林昌[10]研究成果正态、对数正态分布特性的对比完全而且唯一受控于变异系数，在实际应用中，当变异系数<30%且偏度系数<0.025时，选择正态分布，反之，选择对数正态分布。通过表1可得，天然c值和饱和c值选择对数正态分布，而天然φ值和饱和φ值选择正态分布。

通过对c和φ进行相应的处理后，随机获取12 000组数据所得c和φ值概率密度分布见图2。

图2 考虑变异系数和偏度系数c和φ值概率密度分布

根据岩土规范[15]的规定，当滑动面为折线形时，可采用传递系数法(推力传递法)计算滑坡稳定性，并考虑以下5种工况进行稳定性计算。

工况1：145 m水位+自重+地表荷载；

工况2：175 m水位+自重+地表荷载；

工况3：145 m水位+自重+地表荷载+地震+暴雨；

工况4：175 m水位+自重+地表荷载+地震+暴雨；

工况5：175 m水位骤降至145 m水位+自重+地表荷载+暴雨。

根据产生的12 000组c，φ值随机抽取代入传递系数公式中可得藕塘滑坡的稳定系数，并由公式(4)可计算得失稳概率见表2。

在模拟过程中将采用多次多组蒙特卡洛(Monte-Carlo)模拟，在输入不同的N值时，计算得出的失稳概率有一定程度的差异。从图3(a)可以看出在前400次模拟过程中，滑坡失稳概率极不稳定。从图3(b)可以看出：当模拟次数超过1 000次以后，滑坡失稳概率已经趋于稳定状态。

表2 考虑变异系数和偏度系数计算得到的失稳概率

图3 输入不同模拟总次数时的失稳概率

3.4 不考虑变异系数和偏度系数计算滑坡失稳概率

如果不考虑岩土体参数的变异系数和偏度系数，均为正态分布，同样采用Box和Muller提出的变换法，对滑带土的参数进行处理，则天然c值和饱和c值的概率密度分布如图4所示。

图4 不考虑变异系数和偏度系数c值概率密度分布

同理根据岩土规范的规定，当滑动面为折线形时，可采用传递系数法(推力传递法)计算滑坡稳定性，并计算出滑坡失稳概率见表3。

表3 不考虑变异系数和偏度系数计算得到的失稳概率

3.5 2种情况对比分析

通过对2种不同情况的失稳概率计算可知，2种情况所得出的失稳概率完全不同，结果表明，不考虑变异系数和偏度系数计算得出的滑坡失稳概率比考虑变异系数和偏度系数计算得出的滑坡失稳概率较高，见表4。

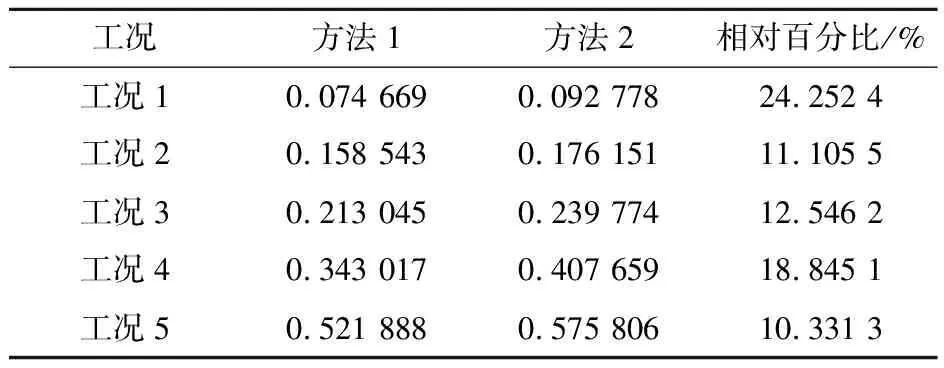
表4 2种方法失稳概率

由表3和图5可得，如果不考虑变异系数和偏度系数计算出的失稳概率将比考虑变异系数和偏度系数偏大，其分析原因可能是由于当岩土体参数的变异系数>30%且偏度系数>0.025时，采用正态分布，可能导致岩土体参数的分布较大，甚至产生负数(如图4)。而如果采用对数正态分布，则岩土体参数分布相对集中，且不产生负数(如图2(a),(b))。岩土体参数c和φ值变小，则导致稳定性系数变小，失稳概率变大。

图5 2种方法失稳概率对比

根据表4相对百分比可得，2种方法的相对百分比为10%～25%，说明在该种情况下岩土体参数c和φ值服从不同分布形式时，可能导致的误差为10%～25%。而较严春风等[9]所得的计算误差(可达20%～30%)偏小，其原因可能是由于本文在c和φ值服从何种分布时，考虑c和φ值的变异系数和偏度系数，而φ值的变异系数<30%和偏度系数<0.025，所以没有改变其分布形式，只改变c值的分布形式，导致误差偏低。

4 结 论

本文基于蒙特卡洛法对藕塘滑坡失稳概率计算，弥补了传统观念对滑坡失稳判断(Fs>1时滑坡处于稳定状态，Fs<1时滑坡可能失稳)的不足，对工程实例有一定的参考价值和意义。

(1) 通过对藕塘滑坡失稳概率计算可得，在175 m水位骤降至145 m水位+自重+地表荷载+暴雨工况下，藕塘滑坡的稳定系数为0.993 43，失稳概率为0.521 888，失稳可能性极大。

(2) 如果考虑岩土参数分布形式，不考虑变异系数和偏度系数计算出的失稳概率将比考虑变异系数和偏度系数计算出的失稳概率相对较高。

(3) 通过对c和φ值在正态分布和对数正态分布的处理下，若考虑c和φ值的变异系数和偏度系数使用分布形式，2种失稳概率误差在10%～25%之间，与严春风等研究结果大致吻合。

参考文献：

[1] 李 猛.边坡稳定可靠度的蒙特卡罗数值模拟及其应用研究[D] .河南：郑州大学，2004: 5-24.(LI Meng. Numerical Simulation on Slope Stability Reliability by Monte-Carlo Method and Application[J]. Henan: Zhengzhou University, 2004: 5-24.(in Chinese))

[2] 贾鹏云，杜 宇.蒙特卡洛法在发耐斜坡稳定性评价中的应用[J] .路基工程，2010，(2)： 127-129.(JIA Peng-yun, DU Yu. Application of Monte-Carlo Method in Evaluation of Fanai Slope Stability[J]. Subgrade Engineering，2010，(2): 127-129. (in Chinese))

[3] 徐钟济.蒙特卡罗方法[M] .上海：上海科学技术出版社，1985：156-162. (XU Zhong-ji. Monte-Carlo Method[M]. Shanghai: Shanghai Scientific and Technical Publishers, 1985: 156-162. (in Chinese))

[4] 赵寿刚，兰 雁，沈细中，等.蒙特卡罗法在土质边坡可靠性分析中的应用[J] .人民黄河，2006，28(5)：65-66.(ZHAO Shou-gang, LAN Yan, SHEN Xi-zhong,etal. Monte-Carlo Method in Reliability Analysis of Earth Slopes Application[J]. Yellow River, 2006, 28(5): 65-66.(in Chinese))

[5] 许英姿，余宏明，唐辉明.蒙特卡罗法在某厂区土坡稳定性评价中的应用[J] .水文地质工程，2002，(2)：49-52.(XU Ying-zi, YU Hong-ming, TANG Hui-ming. Application of Monte-Carlo Method to a Slope Stability Assessment[J]. Hydrogeology and Engineering Geology, 2002，(2)：49-52. (in Chinese))

[6] 许文达.基于蒙特卡洛一有限元法的边坡可靠度分析[J] .福州大学学报(自然科学版)，2004，(2)：73-77.(XU Wen-da. Reliability Analysis of Slope Based on Monte-Carlo Finite Element Method[J]. Journal of Fuzhou University(Natural Science)，2004，(2)：73-77. (in Chinese))

[7] 陈 伟，许 强，王新平.单体滑坡灾害危险性评价方法研究[J] .地质与环境，2011，39(4)：561-566.(CHEN Wei, XU Qiang, WANG Xin-ping. Study on the Method of Hazard Assessment for Single Landslide[J].Earth and Environment, 2011，39(4)：561-566. (in Chinese))

[8] 刘 鑫.单体滑坡风险评价方法研究[D] .武汉：中国地质大学，2008. (LIU Xin. Methods of Landslide Risk Assessment[D]. Wuhan: China University of Geosciences, 2008. (in Chinese))

[9] 严春风，刘东燕，张建辉，等.岩土工程可靠度关于强度参数分布函数概型的敏感性分析[J] . 岩石力学与工程学报，1999，18(1)：36-39.(YAN Chun-feng, LIU Dong-yan, ZHANG Jian-hui，etal. The Susceptibility Analysis of Reliability for the Probability Distribution Types of Parameters in Strength Criterion [J]. Chinese Journal of Rock Mechanics and Engineering, 1999，18(1)：36-39. (in Chinese))

[10] 张继周, 缪林昌.岩土参数概率分布类型及其选择标准[J] .岩石力学与工程学报,2009，28(增2)：3526-3532.(ZHAN Ji-zhou, MIAO Lin-chang. Type of distribution and Selection Criteria of Soil Parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2009，28(Sup.2)：3526-3532. (in Chinese))

[11] 祝玉学.边坡可靠性分析[M] .北京：冶金工业出版社，1993. (ZHU Yu-xue. Slope Reliability Analysis[M]. Beijing: Metallurgical Industry Press, 1993. (in Chinese))

[12] 罗文强，龚 珏.Rosenblueth方法在斜坡稳定性概率评价中的应用[J] .岩石力学与工程学报,2003，22(2)：232-235.(LUO Wen-qiang, GONG Jue. Application of Rosenblueth Moment Estimation Method to Probabilistic Analysis of Slope Stability[J]. Chinese Journal of Rock Mechanics and Engineering，2003，22(2)：232-235. (in Chinese))

[13] 陈祖煜.土质边坡稳定分析——原理·方法·程序[M].北京：中国水利水电出版社，2003. (CHEN Zu-yu. Earth Slope Stability Analysis: Principle, Method, and Procedures[M]. Beijing: China Water Power Press, 2003. (in Chinese))

[14] 陈 伟，许 强，王朝阳.蒙特卡洛在滑坡稳定性可靠度分析中的应用[J] .路基工程，2011，(4)：135-137.(CHEN Wei, XU Qiang, WANG Zhao-yang. Application of Monte-Carlo Method in Reliability Analysis of Slope Stability[J]. Subgrade Engineering，2011，(4)：135-137. (in Chinese))

[15] GB50021—2001，岩土工程勘察规范 [S] .北京：中国建筑工业出版社, 2009. (GB50021—2001, Specification of Geotechnical Investigation[S]. Beijing: China Architecture & Building Press, 2009. (in Chinese))