双层模糊评价模型在教师教学考核评定中的应用

宋卫华,张 青

黄山学院信息工学院程,安徽黄山,245021

双层模糊评价模型在教师教学考核评定中的应用

宋卫华,张 青

黄山学院信息工学院程,安徽黄山,245021

教师教学考核评定属于多因素综合评价问题，为增加评定的准确性、科学性，提出了基于模糊数学的双层模糊评价模型，阐述了该模型在教师教学考核评定中的具体实施过程，并通过实例计算，说明该模型能对教师教学考核做出科学、客观的评价。该模型还可推广应用于学生实习、实训考核，学校人才测评以及学生毕业设计成绩评定等众多工作中，因此具有一定的实际应用价值。

模糊数学；双层模糊评价模型；教师教学考核

模糊数学的核心理论是以模糊集合代替经典数学中的分明集合，对元素与集合之间的隶属关系进行一种模糊划分，用区间的值表示隶属的程度(或称可能性或称概率)，目前已被应用于模糊控制、模糊识别与决策、模糊检索、气象、生物医学等领域。在国外，模糊数学的应用发展较快，英国伦敦大学开发出了世界上第一个模糊控制系统，美国把模糊逻辑应用于航天飞机的对接及卫星跟踪系统中。在国内，刘应明教授对模糊拓扑学，张文修对模糊测度等都有深入的研究；除此之外，还有一些在气象、控制等方面的具体研究成果[1]。然而，模糊数学中一个很重要的应用分支是模糊计算机功能进行综合评价或评判[2-3]，其中模糊综合评价法是应用模糊数学理论依据多种评价因素(或标准)和实测值, 经模糊变换后对事物作出综合评价，进而提高判断的真实性、准确性和公平性。

教师教学考核是高校教学质量管理中一项非常重要的工作，也是引导教师重视教学，进而提高教学质量的重要途径。因为教师的教学效果直接影响学校的教学质量，也间接影响学校的招生与就业，可以说教师教学与学校的未来息息相关，尤其是应用型本科院校。然而教学考核是一个非常复杂的过程，受多种模糊因素的影响[4]。为此，本文结合模糊数学中的模糊评价方法，提出了基于模糊评价算法的双层评价模型，并详细阐述了该模型在教师教学考核评定中的具体应用过程。

1 模糊评价算法的数学模型

模糊评价算法通过综合考虑事物的多种因素，进而作出一种全面的评价，其本质是一种基于多因素的评价决策方法。

1.1 构建因素集U及权重集

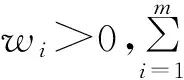
1.2 构建评价集和评价值集合V′

若对事物的评价分为不同的等级，则可构建评价集V={vj,j=1,2,…,n},其中n代表评价等级的个数。有时候，若想得到具体的数值表示，则可通过评价集赋值法可构建评价值集合,V′={vj′,j=1,2,…,n},其中n代表评价值的个数。可见评价值集合V′与评价集V相对应。

1.3 构建模糊关系矩阵R

由上述因素集U和评价集V可构建模糊关系矩阵R，其中元素rij可记为：

(i=1,2,…,m;j=1,2,…,n)

(1)

其中,对于R中的每一行ri={ri1,ri2,…,rin}代表从因素ui出发对要评价的事物参照评价集V作出的评价结果。实际应用时，一般取

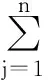
1.4 模糊运算

当因素权重集及模糊关系矩阵确定后，可通过模糊运算(变换)对事物进行综合评价,得到模糊评价集:

(2)

则bj为全面考虑多种因素及其影响权重不同时，作出的综合评价结果集合。bj反映了事物对评价等级集中元素vj的隶属度。由最大隶属度原则，B中数值最大者所对应的评价等级即为最终的评价结果。

2 模糊评价法在教师教学考核评定中的应用

2.1 构建基于模糊数学的双层模糊评价模型

依据模糊评价模型，先确定教学考核评定中的因素集，其中因素集权重的确定采用专家打分法，同时结合学校针对教师教学考核评价标准；评价结果集采用四级制，即优秀，100≥S≥90；良好，90 >S≥80；合格，80>S≥60；不合格，S<60。实际应用中，为了确保评价的准确性，一个宽泛的因素集(外层因素集)往往又细分为多个更精确的因素集(内层因素集)，为此本文提出双层因素集评价模型，详细的设计见表1所示。

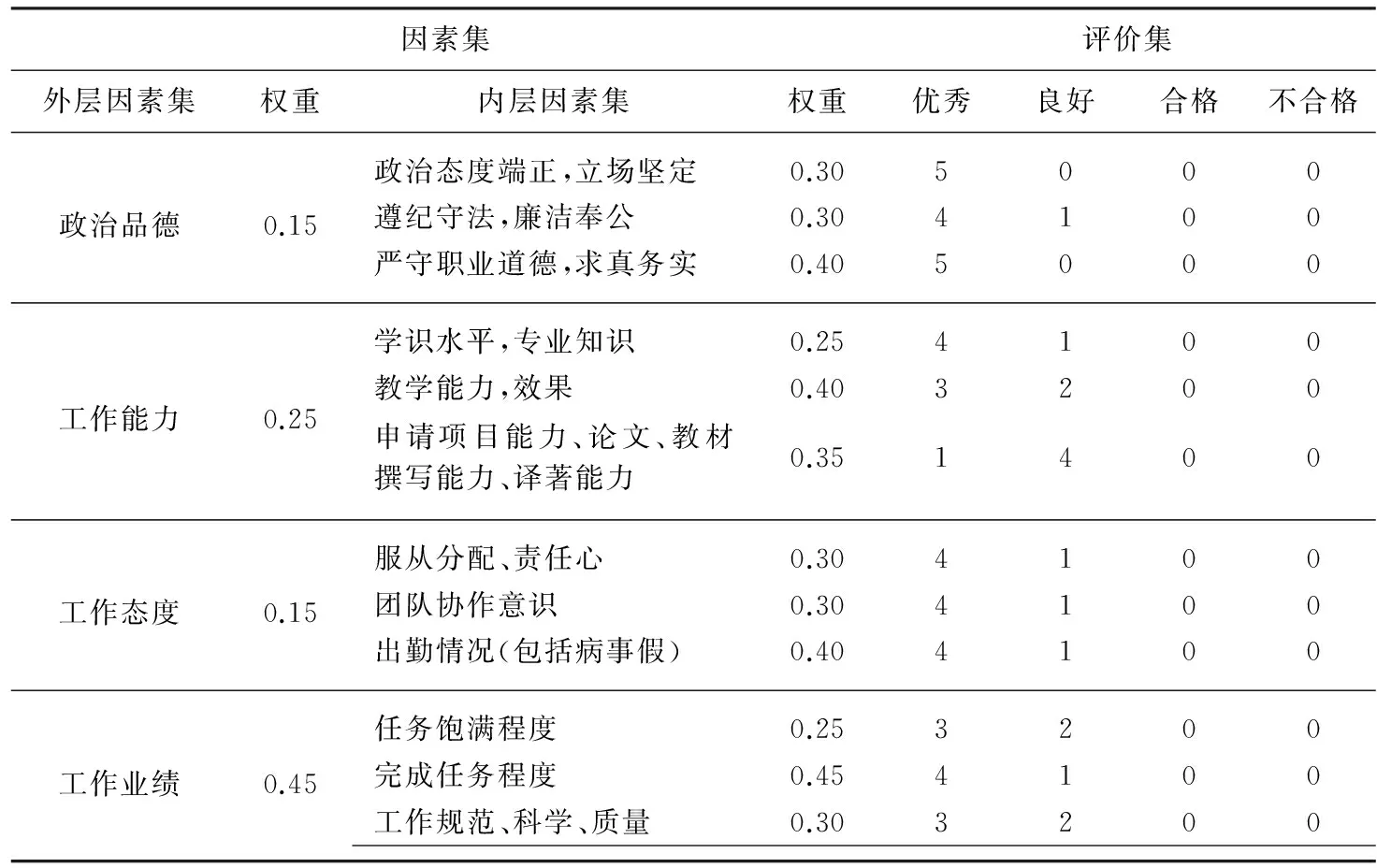
表1 教师教学考核双层评价模型设计及部分评价数据

由表1可知，双层因素集中，外层因素集U={u1,u2,u3,u4}={政治品德，工作能力，工作态度，工作业绩}，其对应的权重集W={w1,w2,w3,w4}={0.15,0.25,0.15,0.45}，其中政治品德、工作能力、工作态度和工作业绩评价又分别包含下列内层因素集：

u1={u11,u12,u13}={政治态度端正，立场坚定；…；严守职业道德，求真务实}，其对应的权重集w1={w11,w12,w13}={0.30,0.30,0.40}

u2={u21,u22,u23}={学识水平，专业知识；…；申请项目能力、论文、教材撰写能力、译著能力}，其对应的权重集w2={w21,w22,w23}={0.25,0.40,0.35}

u3={u31,u32,u33}={服从分配、责任心；…；出勤情况(包括病事假)}，其对应的权重集w3={w31,w32,w33}={0.30,0.30,0.40}

u4={u41,u42,u43}={任务饱满程度；…；工作规范、科学、质量}，其对应的权重集w4={w41,w42,w43}={0.25,0.45,0.30}

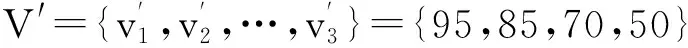
2.2 计算实例

双层评价模型的计算过程由内层因素集向外层因素集逐一计算得到。下面以某院系对某教师的教学考核评定为例(评价数据见表1，其中评价数据是由五位老师组成的院系测评小组对该教师依据相应因素评定为相应等级的人数)，分析模糊评价算法在教师教学考核评定中的具体实施过程。依据表1，在对评价矩阵进行归一化的基础上可计算出政治品德、工作能力、工作态度和工作业绩单因素评价集，即：

政治品德评价B1=政治品德内层权重向量w1·政治品德内层评价矩阵r1，即

=[0.94 0.06 0 0]

(3)

工作能力评价B2=工作能力内层权重向量w2·工作能力内层评价矩阵r2，即

=[0.51 0.49 0 0]

(4)

工作态度评价B3=工作态度内层权重向量w3·工作态度内层评价矩阵r3，即

=[0.8 0.2 0 0]

(5)

工作业绩评价B4=工作业绩内层权重向量w4·工作业绩内层评价矩阵r4，即

=[0.69 0.31 0 0]

(6)

上述计算出的政治品德评价B1、工作能力评价B2、工作态度评价B3、工作业绩评价B4即为依据内层因素集的模糊评价结果，最后根据外层评定因素集及权重集可得：

综合评价B=外层权重向量W·内层评价矩阵R，即

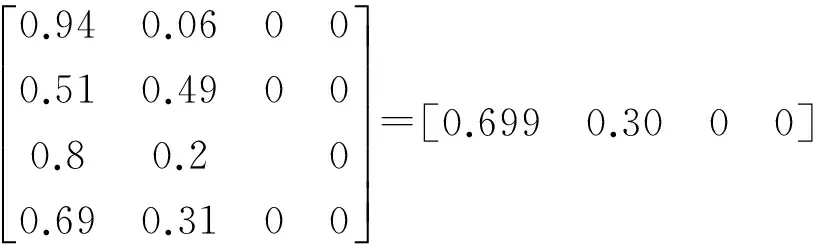
(7)

根据最大隶属度原则，该教师教学考核综合评价等级为“优秀”。若要得出比较具体的分数，可通过评价值集合V′评价集赋值法，则可计算该教师教学考核的综合评分S为：

S=B·V′T=[0.699 0.301 0 0]·

[95 85 70 50]T=91.99

(8)

此分值与打分制的评价结果非常接近，并且综合评价后所属等级完全相同，因此可以表示最终结果。

3 结束语

教师教学考核是一个复杂的过程，受多种模糊因素的影响，文中提出了基于模糊数学的双层模糊评价模型，并通过实例阐述了该模型在教师教学考核评定中的具体应用。该模型便于在计算机上开发应用，只要设置好相应参数，在线输入评价数据，则计算机就可自动计算出对教师教学考核的综合评价结果，体现了教学考核的科学性、公正性。为此，下一步的工作是开发出一个基于双层模糊评价模型的应用系统，并应用到教师的教学考核评定中。另外，该模型也可推广应用于学生实习、实训考核，学校人才测评以及学生毕业设计成绩评定等[5-6]众多工作中，具有一定的实际应用价值。

[1]谢季坚,刘承平.模糊数学方法及其应用[M].2版.武汉:华中理工大学出版社,2000:1-52

[2]汪培庄,李洪兴.模糊系统理论与模糊计算机[M].北京:科学出版社,1996:472-509

[3]廖梦怡,申远.基于Fuzzy数学评价模型的本科毕业设计质量评价系统研究[J].计算机与数字工程，2014,4(2):248-250

[4]段赵磊,徐洁.基于Borda数—模糊数学的双层教学质量评价系统研究[J].中国电力教育，2013(11):27-28

[5]张志英.模糊评价法在本科毕业设计成绩评定中的应用[J].浙江理工大学学报,2011,28(3):467-470

[6]林东榕.模糊数学理论在人才测评中的应用：高校科研人才业绩的主观综合测评量化方法研究[J].广西工学院学报,2006,17(2):67-70

(责任编辑：刘小阳)

10.969/j.issn.1673-2006.2014.11.030

2014-07-15

黄山学院科研项目“基于HTML5/CSS3的中小型管理企业前台框架设计”(2014xkj004 )；黄山学院大学生创新训练项目“.NET平台下学生综合测评系统的开发”(AH201310375057)。

宋卫华(1982-)，河南商丘人，硕士，助教，主要研究方向：数字图像处理、数据库。

G451.1

A

1673-2006(2014)11-0103-03