后横向推力杆失效分析与改进
2014-08-16杨丽群
杨丽群
安徽交通职业技术学院汽车与机械工程系,安徽合肥,230051
后横向推力杆失效分析与改进
杨丽群
安徽交通职业技术学院汽车与机械工程系,安徽合肥,230051
五连杆非独立悬架的后横向推力杆在弯道和坑洼多的off-road路面上试验时出现弯曲现象。从结构力学计算截面系数,进而进行CAE屈曲强度和复合工况下的应力值分析以及固有频率分析,找到后横向推力杆失效的原因。最终提出将横截面由原来U型的冲压件改成圆钢的优化设计方案。台架疲劳试验及整车振动试验结果表明,改进后横向推力杆强度更高,疲劳性度大幅提升,杆子固有频率的变化也未放大后悬架的共振。结果显示,提升悬架连杆强度最重要的方法是增大连杆的截面系数,这对解决类似问题具有一定的参考价值。
后横向推力杆;断裂;强度分析;固有频率;共振
五连杆非独立悬架带横向推力杆在很多SUV、MPV等后驱车型上运用较广泛,它配合后整体桥,在保证整车承载性的同时,也拥有很好的舒适性能和操稳性能。后横向推力杆,在一些文献资料中也称潘哈杆(panhard rod),一般布置在后桥的后方,增大不足转向趋势[1-2]。在车辆转向时,杆子本身主要受侧向拉力与压力,在车辆制动或悬架上下跳时,主要受X向和Z方向的弯矩。后横向推力杆一般采用两种结型式,一般为冲压焊接型式,另一大类主要是圆型空心钢管。整车行驶时,横向推力杆会与动力传动系共振问题,这时通常会在横拉杆上增加一个谐振块,谐振块频率与共振频率相等,可将共振的能量峰值消除或减弱。
本文以某车型后横向推力杆原设计为U型截面的冲压件,在多弯、坑洼的off-road路面上试验时出现弯曲、断裂的现象为背景,通过力学计算与强度校核,提出两种设计改进思路,并通过台架疲劳试验和振动测试对比,改进后的效果非常好。
1 结构力学分析
一个典型的后五连杆悬架非独立悬架的3D图如下图1所示,在路试过程中出现后横拉杆弯曲的故障图片如下图2所示,弯曲部位主要在杆子中段,呈典型强度不足造成的失效。
现有后横向推力杆为U型横截面,开口向下,为板材冲压成型,材料SS400,屈服极限为235 MPa。弯曲的后横向推力杆材质化验合格,材料符合设计要求。类似的横拉杆也可采用空心圆钢的结构设计。有些资料通过欧拉公式计算压缩失稳时的载荷大小来判定强度大小[3]。
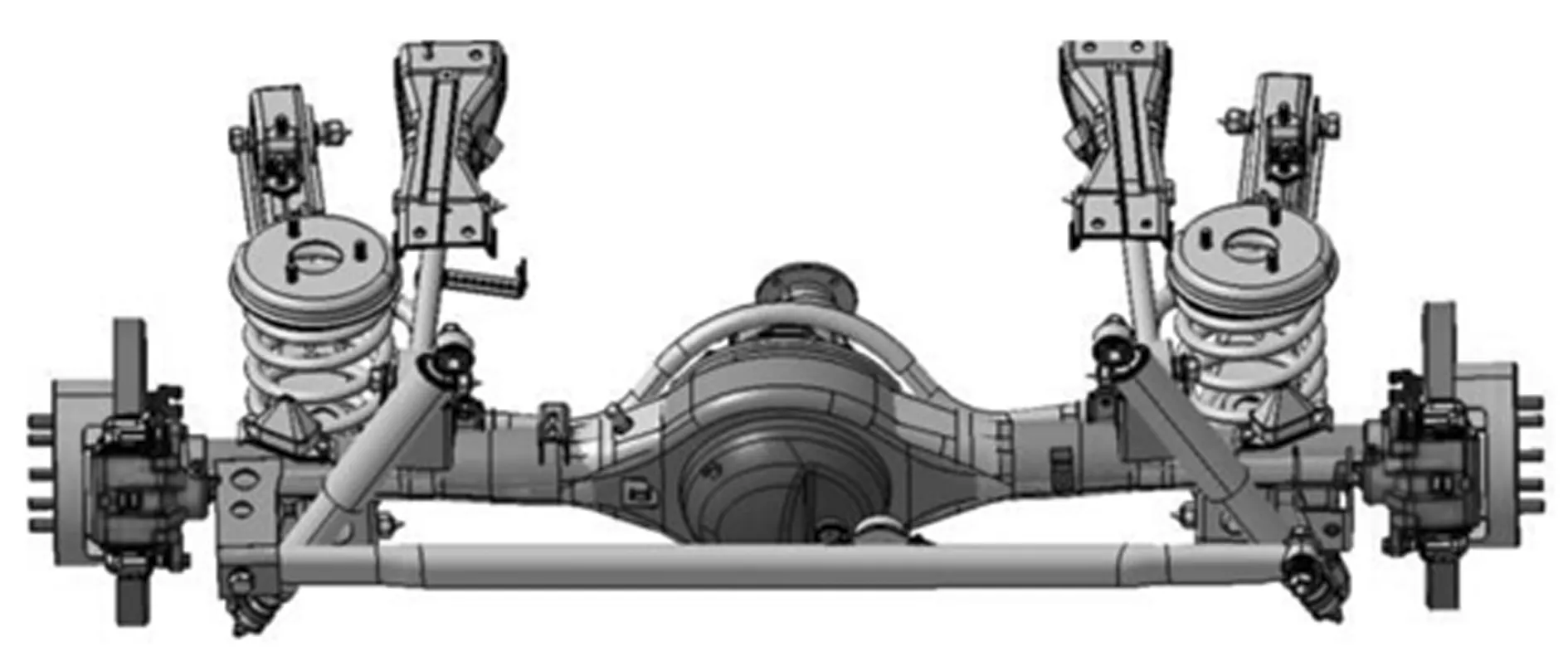
图1 五连杆非独立悬架

图2 后横拉杆弯曲照片
本文从杆的截面系数和惯性积出发,由机械几何和工程力学知识可知,抗弯截面系数在横截面上离中性轴最远点处,弯曲正应力最大,其值为[4-5]:
比值Iz/ymax仅与截面的形状与尺寸有关,称为抗弯截面系数,并用Wz表示,即
由公式可见,最大弯曲正应力与弯矩成正比,与抗弯截面系数成反比。抗弯截面系数Wz综合反映了横截面的形状与尺寸对弯曲正应力的影响。U型、圆薄壁梁抗弯截面系数分别如图3(A)(B)。

图3 U型、圆薄壁梁剖面图
空心圆管梁Φ30.0 mm×4.0 mm:
U型梁可以简化成矩形开口梁:36mm×41mm×3.0mm:

最终考核杆子抗弯能力主要看Wz的大小,代入数值计算后发现,U型梁的Wz为565.7mm3,而空心圆管钢的Wz为1 882.9mm3,所以在同一个悬架结构及固定的受力比如相同的弯矩条件下,圆钢最大应力是U型梁的1/3。计算结果表明,圆钢的强度远高于U型冲压件,下一步改进的方向是将U型的后横向推力杆改为圆型空心钢管的结构。
2 CAE强度分析
基于上述结构力学的理论计算与分析,提出两个后横向推力杆的改进方案如表1所示:一是在冲压件中增加圆钢;二是将冲压件整体改成圆钢。
表1 两种改进方案与原方案对比

2.1 屈曲能力分析
模拟一端加载,让杆子变形15 mm,考核杆子的屈曲形态及最大应力。从图4可以看出,原横拉杆在变形的弯曲形态与实际路试弯曲形态一致。另外,方案二(圆钢)在屈曲15 mm时,最大应力在375 Mpa,远小于原来横拉杆的1 055 Mpa及优化方案一的1 570 Mpa。

图4 屈曲分析应力分布对比图
2.2 模态与频率分析
因杆子刚性加强,重量变轻,圆钢整体的一阶频率由原67.4 Hz提升到97.8 Hz,如图5所示,理论上是可以取消原来杆子上的谐振块,但需要实际对比测试后悬的噪音与振动情况。

图5 一阶弯曲频率对比图
2.3 整车复合工况模拟分析
目前,悬架部件的强度分析多从单工况提取力来分析[6],部分文献也有提到复合工况法[7],每个车型具体的问题可以根据实际的路况来制定相应的工况计算方法。由于弯曲故障发生于OFF-ROAD路况,故本文提出以下四种新的复合工况分析:
(1)左转弯掉坑(转弯0.8 g加垂直3.5 g)。
(2)右转弯掉坑(转弯0.8 g加垂直3.5 g)。
(3)倒车转弯(先倒车制动-1 g再右转弯0.8 g)。
(4)倒车掉坑(先倒车制动-1 g再垂直3.5 g)。
虽然(4)工况在实际试验及使用中达不到,但可作为寻找最极限受力条件参考。对比三种设计方案,在(3)、(4)工况下的应力情况如表2所示。
可见两个极限复合工况下,改进方案二的应力最小,远小于材料35#钢的屈服极限315 Mpa,此设计的安全系数最高。综合理论计算与CAE的强度分析,最终选择方案二,即采用圆钢Φ30 mm×4.0 mm来改进实施。

表2 三种方案的复合工况强度对比

图6 台架疲劳加载与装夹
3 台架疲劳试验
横向推力杆的台架试验:一端固定,一端加载轴向力FY=±20 800 N,两端均不带弹性衬套,钢性连接在夹具上。轴向力FY为整车受到单工况最大轴向拉压力,加载频率为3 Hz,目标次数为30万次以上。结果:原设计试验次数为33 707次,U型梁与衬套套管焊接处开裂;改进后的圆钢是衬套钢管开裂,次数为422 898次,可见疲劳性能大幅度提升(图6-8)。

图7 原设计台架失效图

图8 圆钢台架失效图
4 振动对比测试
首先对新旧两样件进行整车装配状态固有频率敲击试验,后在样件中间贴一传感器,车内中排座椅导轨和后排座椅导轨分别贴一传感器,对新旧件进行3WOT、怠速及60 Km/h匀速试验,了解各工况下后横拉杆的振动情况。两件在装配约束状态Z向,旧件固有频率为60.61 Hz,而新件Z向的固有频率降为53.48 Hz,如图9所示。

图9 后横向推力杆Z向固有频率
在220 Hz,新横拉杆还存在二阶固有频率,此频率对应的转速较高,在6 600 rpm左右,一般车型达不到此高转速;3WOT在某一转速能激起后横拉杆固有频率而产生大幅振动,由图10可知,旧件共振转速为1 863 rpm,而新件共振转速为1 623 rpm,且Z向振幅为老件的2.4倍,工况有所恶化,X、Y向共振能量不大,在此不作过多的论述和对比。

图10 后横向推力杆共振振幅及转速
中排座椅新旧件对比:由图11可知,更换新件后X、Y向振动加速度减小明显,而Z向振动加速度略微减小。

图11 中排座椅振动对比

图12 后排座椅振动对比
后排座椅导轨上的振动新旧件对比,由图12可知,新件状态下后排座椅导轨振动加速度明显变大,在发动机转速为1 637 rpm时,Z向存在明显峰值,这主要是由后横拉杆发生共振引起,但此振动值绝对量0.18 g并不大,通过座椅隔振衰减后对后排乘客影响不大。通过振动对比测试发现,改进的后横拉杆装配约束状态下,Z向的固有频率改变,引起的共振转速降低,避开常用转速区域,中排座椅振动加速度减小,后排座椅振动加速度增大,但因其绝对值较小,对后排乘客舒适性并无影响,考虑成本原因,也没有必要在新的横向推力杆上重新设计谐振块。
5 结束语
后横拉杆弯曲的主要原因是本身截面系数小,在极限复合工况下应力超出材料的屈服极限造成弯曲,进而产生疲劳断裂。通过力学计算和复合工况的CAE对比分析,找到最优改进方案,台架疲劳试验和振动对比测试结果表明,改圆钢后的横向推力杆强度大幅提升,固有频率降低,错开常用转速区间,中排振动略有改善,后排座椅振动效果相当。当然,后横向推力杆也可以再设计一个谐振块来进一步降低共振能量,进而提高舒适性,这取决于设计成本。
[1]耶尔森,赖姆帕尔.汽车底盘基础[M].北京:科学普及出版社,1992:32-33
[2]潘筱,王冬成,林逸,等.用多体动力学方法分析五连杆非独立后悬架的随动转向特性[J].汽车工程,2013(4):331-335
[3]丁向东.横拉杆断裂原因分析与改进[J].客车技术,2010(3):43-44
[4]沈鸿.机械工程手册[M].北京:机械工业出版社,1982:181-190
[5]罗迎社.工程力学[M].北京:北京大学出版社,2006:90-97
[6]豆力.轿车扭转梁悬架强度分析与疲劳寿命预测[J].客车技术,2012(5):12-14
[7]方其让,苏嘉理,刘诗云.某微型客车后悬架横拉杆支架断裂分析及改进[J].汽车技术,2006(12):24-26
(责任编辑:汪材印)
宿州学院再获得多项安徽高校人文社会科学重点研究基地招标项目
根据安徽省教育厅《关于下达2014年度安徽高校人文社会科学重点研究基地招标项目的通知》,宿州学院大学文化研究中心和皖北城乡一体化研究中心两个省高校人文社科重点研究基地共计6项科研课题获批重点项目立项,其中校外课题1项,本校课题5项。
10.3969/j.issn.1673-2006.2014.11.025
2014-06-18
杨丽群(1981-),女,安徽安庆人,硕士,讲师,主要研究方向:汽车维修。
U46
A
1673-2006(2014)11-0086-03
