基于贝叶斯分析框架下的VAR和DSGE模型①
2014-08-16阳晓明
阳晓明
(湘潭大学商学院,湖南湘潭411105)
1 引言
宏观经济学在20世纪30年代“凯恩斯革命”中成为独立的研究领域。应用宏观经济学一直是宏观经济学中最为活跃的研究领域之一,各种新思路、新方法层出不穷。“凯恩斯革命”之后的几十年中,由凯恩斯理论导出的结构方程方法成为宏观经济学实证研究的主要方向。但是20世纪70年代由于受到卢卡斯批判(Lucas critique)和宏观经济模型商业应用的冲击,考尔斯委员会(Cowles commission)结构性联立方程组模型逐渐失去其在应用宏观经济学中的统治地位。20世纪80年代以后,由于Kydland and Prescott(1982)和Long and Plosser(1983)的开创性工作,第一代动态随机一般均衡(DSGE)模型以(Kydland and Prescott为代表的RBC模型)成为宏观经济学的主流理论方法,许多实证宏观计量方法也围绕如何估计和评价DSGE模型展开[1]。
在实证宏观计量方法方面,经济学家提出了许多正式和非正式的数量方法,如向量自回归(VAR)方法、校准(calibration)方法、一般矩估计方法(GMM)及完全信息极大似然估计(MLE)方法等等。为了减轻“经济理论施加的难以置信的限制”,Sims(1980)提出较少运用经济理论而以数据为中心的VAR方法,该方法自提出以来得到了广泛的运用,并成为宏观经济建模的基本分析工具。DSGE模型是一个数据生成过程的多元随机表示系统,这使我们很容易将其近似表示为VAR模型[2]。但是,简单的DSGE模型对数据施加了很强的限制和约束条件,因而存在严重的模型误设定(mis-specificaiton)问题,这使得由DSGE模型所导出的VAR模型常常被实际数据所拒绝(An and Schorfheide,2007)。正是由于模型误设定和识别等问题,经济学家们在80年代对DSGE模型的评价一直没有有效的正式统计学方法,这也是Kydland and Prescott(1982,1996)放弃正式的(概率)计量方法,转而使用非正式的计量方法-校准方法的原因。与概率方法对计量经济模型的估计、检验和统计推断不同,校准方法通过选择宏观经济数据(如国内生产总值、通货膨胀等)的一些特征化事实(如一阶矩、二阶矩等),设定DSGE模型的参数使模型理论矩与观测到数据的相应矩(特征化事实)相一致,并验证模型能否解释剩下的特征化事实(如各种高阶矩)。但是在校准方法中,参数值和特征化事实的选取往往是任意的,没有固定的选择程序;而且该方法没有参数估计结果的概率度量和统计检验。上述问题都使得校准方法缺乏稳健性和统计推断能力,而对于引入大量刚性和冲击的大规模新凯恩斯主义DSGE模型来讲,校准方法就变得更加难以执行,而且上述缺点将变得更为严重。
Hansen(1982)提出的GMM方法则从一定程度上缓解了校准方法缺乏概率描述的缺点。GMM方法从某些总体距条件(正交条件)出发,使样本距与总体距尽量相一致或靠近,以此估计模型参数。但是由于工具变量的可获得性、小样本偏差和最优权重矩阵的估计等问题使得GMM方法缺乏可行性和稳健性。而且在宏观经济运用中,由于该方法使用DSGE模型的欧拉方程矩条件而无需解出模型,这就使模型的识别问题显得更为突出(Canova,2007)。Linde(2005)使用模拟数据发现即使没有测量误差,新凯恩斯主义菲利普斯曲线模型的GMM估计量在小样本时也有严重的偏差,而且偏差程度随货币政策行为的变化而变化,而此时完全信息极大似然估计则更具有吸引力。传统的完全信息极大似然估计方法首先需要对DSGE模型的外生冲击设定一个概率分布,然后根据模型的结构方程推导出似然函数,并在一定的参数空间内极大化该似然函数。Linde(2005)发现无论在模型误设定还是非正态测量误差条件下,完全信息极大似然估计都比有限信息方法(如GMM)表现更好。但是由于DSGE模型非线性解的计算负担,使得大多数经验文献仅仅能估计线性化的DSGE模型。而且非高斯扰动的DSGE模型、似然函数的扁平性(flatness)和多重局部极大值问题等也常常使得极大似然估计难以进行。另外极大似然估计方法对模型误设定非常敏感,只有在模型有很好的线性近似,且模型误设定很小时才能运行良好[3]。
同时宏观经济学家们通过不断引入一些更为实际的假定条件,使得模型的设定能进一步逼近现实经济运行,这大大改善了第一代DSGE模型的误设定问题,也使得一些传统的计量经济技术能用来估计、评价和预测DSGE模型。如贝叶斯VAR方法、贝叶斯DSGE方法、基于DSGE和VAR冲击响应函数差距的最小距离估计方法等等,其中贝叶斯VAR和贝叶斯DSGE方法得到了学术领域和中央银行实际工作者的广泛认可。
2 贝叶斯分析方法
贝叶斯分析方法是指在进行参数估计时,将参数的某些先验信息考虑进来,将这些先验信息与样本信息相结合,运用贝叶斯定理得出(或更新)参数估计的统计学方法。假定我们要估计的参数为θ,贝叶斯估计方法将其看作随机变量,并假定其概率密度为p(θ)。假定YT表示T个随机样本观测值,则p(YT|θ)为样本的条件概率密度,也是样本观测值的似然函数。p(YT,θ)为样本观测值和待估参数的联合概率密度函数,p(θ|YT)为给定样本信息后参数θ的后验概率密度,由贝叶斯定理有:

其中P(YT)≠0。由于P(YT)与θ无关,可视为常数,将上面表达式写为:

其中∝表示“成比例”,即在给定样本信息后,待估参数的后验概率密度与参数先验概率密度和样本似然函数的乘积成比例。该公式表明先验信息通过先验密度进入后验密度,样本信息通过似然函数进入后验密度,联合后验密度则将所有先验和样本信息归纳融合其中(Zellner,1971)。在贝叶斯观点下,待估计参数被看作随机变量,关于参数的推断都是以概率形式出现的,这使我们可以考虑尽可能大的参数空间,使模型的估计更为稳健。许多数值模拟方法如马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo)都能被用来从参数后验分布中进行抽样,基于这些抽样我们可以通过数值方法来估计后验分布的各种矩,并对参数进行统计推断[4]。
经济学家将贝叶斯观点运用到了许多宏观经济学模型中,近年最主要的进展是贝叶斯向量自回归(贝叶斯VAR)模型和贝叶斯动态随机一般均衡(贝叶斯DSGE)模型。贝叶斯DSGE和贝叶斯VAR方法就是将先验信息引入DSGE和VAR模型,运用贝叶斯观点,使先验信息与数据信息相结合,进而对模型的参数进行后验推断和预测的一种统计推断方法。贝叶斯DSGE和贝叶斯VAR方法不仅有贝叶斯估计方法的一般优点,相对于一般的DSGE和VAR模型,贝叶斯估计方法在模型的估计、评价和计算上也有较多优势。而且贝叶斯估计方法将经济理论、数据和政策分析非常好地融为一体,已成为宏观经济建模和预测,欧、美国家中央银行制定和执行货币政策的基本分析框架。下面以贝叶斯VAR模型和贝叶斯DSGE模型为例,说明其基本原理和运用。
3 贝叶斯VAR和贝叶斯DSGE模型方法
3.1 贝叶斯VAR模型方法
20世纪80年代以后,经济学家广泛运用VAR方法对时间序列进行分析、预测和政策分析。但是,对于由标准DSGE模型得出的限制性简约VAR或拥有较小自由度的VAR来讲,运用非限制性VAR方法进行的实证估计往往不太准确,或预测时有很大的标准差,而且难以形成良好的经济学理论解释。而当数据较少,或样本信息较弱,或待估计参数数量较多时,非限制性VAR估计将带来过度拟和(overfitting)问题及因此导致的较差的预测效果(Canova,2007)。贝叶斯VAR模型则可以很好地解决非限制性VAR模型的样本外预测表现、模型误设定及数据和经济理论一致性等问题。
3.1.1 Minnesota先验分布贝叶斯VAR模型
假定有T个样本观测值的n×1向量yt有以下p阶简约VAR模型表示:
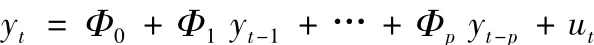
其中Φ0,Φ1,...,Φp为VAR系数参数,ut为向前一步预测误差,ut-N(0,Σu)为了改善VAR模型的样本外预测表现和识别问题,Doan,Litterman and Sims(1984)和Litterman(1986)针对非限制性VAR模型的系数参数提出了Minnesota(或 Litterman)先验分布。定义Φ =[Φ0,Φ1,…,Φ]'、α =vec(Φ)和 YT= [y1,…,yT]',Minnesota先验分布假定α-N(0,Σα),其中α是n2(p+1)×1向量,对角阵Σα是先验方差协方差矩阵,且是少数几个超参数(hyperparameter)的函数。实际上Minnesota先验分布是按逐条方程对简约VAR模型系数参数设定先验信息,因而在多方程结构VAR模型占主要比重的宏观经济研究中有一定局限性。针对多方程结构 VAR模型,Sims and Zha(1998)进一步发展了Litterman的思想,使用“正态 -逆Wishart”先验分布作为结构参数的先验信息,该先验分布也适用于过度识别的结构VAR模型。在实证研究方面,Robertson and Tallman(1999)根据美国主要宏观经济数据,使用 Minnesota、扩展的 Minnesota和 Sims and Zha(1998)等多种先验分布,证实带有先验分布的贝叶斯VAR模型可以很好地提高非限制性VAR模型的预测表现。Cogley and Sargent(2001,2005)和 Canova et al.(2008)等则进一步放松了VAR模型的系数限制。他们允许VAR模型的系数随时间而变化,即时间可变系数贝叶斯VAR模型(TVC-BVAR),以解释观察到的宏观经济时间序列中结构变化和区制转换现象。Minnesota先验BVAR模型可以在一定程度上回避VAR模型中的“维度诅咒”问题,能很好地平衡VAR模型估计中的可靠性和计算负担问题,而且可以提供较好的短期时间序列预测[4]。当然Minnesota先验分布的设定较多地依赖经验方法,缺少经济学解释和理论支撑。先验分布如太松则易造成过度拟合问题,如太紧则易造成数据信息缺失问题,而且忽视了内生变量的联动效应(co-movements)信息[5]。
3.1.2 DSGE -VAR 分析方法
DSGE模型对其移动平均表示参数施加了很强的约束,尽管DSGE模型没有有限阶的VAR表示,我们仍然可以使用p阶VAR模型作为DSGE模型移动平均表示的近似。DSGE模型p阶VAR近似表示的滞后阶数越长,则该近似表示与DSGE模型的误差越小。非限制性VAR模型参数向量比DSGE模型参数向量的纬度大得多,因此DSGE模型对其近似VAR表示施加了很强的结构约束。近年来,越来越多的实证研究表明DSGE模型中潜在的模型误设定问题是不容忽视的Del Negro et al.(2007),因而由非限制性VAR模型推出的冲击响应函数往往与误设定的DSGE模型推出的冲击响应函数有相当大的差距。为了解决DSGE模型的误设定及数据和经济理论的一致性问题,Del Negro and Schorfheide(2004)提出了DSGEVAR分析方法。假定DSGE模型n×1内生可观测向量yt有如(4)式定义的p阶简约VAR近似表示形式,向量θ表示DSGE模型的待估计深层参数,用基于参数θ的DSGE模型产生的T*个模拟样本增广实际样本数据,引入超参数λ=T*/T作为模型误设定的度量指标。假定以参数θ为条件,VAR模型参数的先验分布服从“正态 -逆Wishart”分布形式,则运用贝叶斯定理可以得出VAR模型参 数 Φ 和 Σu的 后 验 估 计 量。DelNegroand Schorfheide(2004)认为可以使用数据驱动的方法确定超参数λ的取值,即最大化超参数λ的边际似然函数
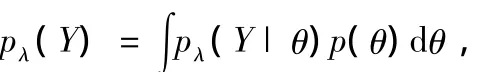
其中pλ(Y|θ)= ∫p(Y|Φ,Σu)p(Φ,Σu|θ)d(Φ,Σu)。
且是超参数λ的函数。函数pλ(Y)衡量了可以在多大程度上放松DSGE模型的限制,以平衡样本内拟合和DSGE模型的复杂性,也可以看作DSGE模型误设定程度的时间序列证据(Del Negro et al.2007)。为了求得最优的由超参数λ表示的模型设定形式,设定超参数λ的格点区间为∧ =(l1,l2,……,lq),l1=n(p+2)/T,lq= ∞。
对该格点区间极大化λ的边际似然函数,则λ的最优估计量^λ由下式定义:

DSGE-VAR方法实际上是将DSGE模型作为VAR模型的先验信息,一方面放松DSGE模型的参数限制,以提高DSGE模型的拟合程度,并修正DSGE模型的误设定;另一方面限制VAR模型的参数自由度,以提高VAR模型的预测表现,并提高VAR模型识别和拟合的精确度,取得理论和数据的一致性和平衡。DSGE-VAR估计方法使我们能够考虑介于DSGE模型和非限制VAR模型之间的模型设定形式,可以在由超参数λ代表的一个连续统的中间模型空间中选择最好的模型设定形式[6]。通过极大化λ的边际似然函数选择超参数λ,此时深层参数θ的后验分布可以被解释为用作相应VAR先验分布的最好DSGE模型设定形式的后验估计,而超参数λ的后验分布则给出了DSGE模型可靠性及所代表的经济约束经验相关性的度量指标。Adjemian and Paries(2008)改进了DSGE-VAR分析,他们认为 Del Negro and Schorfheide(2004)和Del Negro et al.(2007)使用少数几个值以格点化超参数λ,在此基础上通过极大化边际似然函数以求得最优超参数值的方法至少在计算上是无效率的,而且是非贝叶斯观点的。与Del Negro and Schorfheide(2004)依照超参数λ的格点取值作循环估计不同,他们将超参数λ看作另一个深层参数,并对其赋予一定的先验分布信息p(Y),再与其他参数的先验分布信息相结合对模型进行估计和推断。
3.2 贝叶斯DSGE模型方法
在DSGE-VAR方法中,参数由最小化非限制性VAR系数和由DSGE模型导出的近似VAR系数(带有跨方程约束)的差距所决定。与DSGE-VAR方法相比,贝叶斯DSGE估计方法则要求直接拟合所有观测到的时间序列数据,在一定程度上是校准方法和极大似然估计方法的折衷,是动态经济理论、计量经济方法和计算机技术的有机融合。Geweke(1999)认为DSGE模型有两种不同的计量经济解释:弱计量解释和强计量解释。弱计量经济解释主要是指Kydland and Prescott(1982,1996)的校准方法,该方法仅仅提供了数据生成过程的部分描述。而强计量经济解释则提供了数据生成过程的整体描述,因而也更为可信和稳健,主要指的是传统极大似然估计方法和贝叶斯估计方法。
假定用 YT=[y1,...,yT]'表示DSGE模型中n ×1阶可观测向量yt的T个观测值,其联合条件概率密度函数(模型的后验核)为

我们可以由DSGE模型的线性状态空间表示形式,使用卡尔曼滤波(Kalman filter)算法推导联合概率密度函数、卡尔曼滤波更新公式和预测公式。假定DSGE模型深层参数向量θ的先验概率密度为p(θ),由贝叶斯定理及L(θ|YT)=p(YT|θ)
可得参数θ的后验密度函数为

其中L(θ|YT)是基于观测数据的似然函数。首先运用数值方法最大化对数似然函数及对数参数先验密度的和(边际数据密度函数是常数),以获得参数的后验众数θmode:

相对传统极大似然估计方法,㏑p(θ)可以被看作对似然函数的惩罚函数(penalty function)。再将后验众数θmode作为初始值(或其他给定初始值),由MCMC抽样方法(如随机游走Metropolis-Hastings算法),从后验分布中获取抽样,由数值积分方法计算所需参数的各阶后验距和置信区间,并检验其收敛性[7]。最后根据计算的各阶距、置信区间和冲击响应函数,由设定的损失函数(loss function)对模型进行推断和评价。以贝叶斯VAR模型类似,贝叶斯DSGE模型使用参数的一个先验分布作为似然函数的惩罚函数,将数据信息和先验信息相结合,对模型作出估计和推断。与DSGE模型的传统极大似然估计相比,贝叶斯DSGE模型对参数赋予了更为合理的空间,有效地避免了传统极大似然估计中似然函数在某些参数空间的扁平性问题和多重局部极大值问题。而且当模型的误设定程度很高时,极大似然估计方法常常得出荒谬的估计结果,而贝叶斯DSGE估计方法可以有效地应对这类“错误的”模型,它可以运用信息性先验(informative prior)分布,充分考虑到模型的不确定性和模型误设定问题,得出相对合理的估计结果。Smets and Wouters(2003,2007)发展了一个粘性价格和工资的新凯恩斯主义DSGE模型,他们用贝叶斯估计方法分别估计了欧元区和美国的主要宏观经济数据,他们发现新凯恩斯主义DSGE模型能很好地拟合欧元区和美国的时间序列数据。在样本外预测方面,贝叶斯DSGE模型比VAR模型或贝叶斯VAR模型表现更好(有更大的似然函数值)。值得注意的是贝叶斯实证文献中的很多作者都来自美国和欧元区的中央银行,他们估计的贝叶斯DSGE模型正在成为中央银行进行宏观经济分析和预测,并依此制定和执行货币政策的基本分析框架。如Smets and Wouters(2003,2007)估计的新凯恩斯主义DSGE模型,该框架已成为欧州中央银行分析宏观经济波动和经济周期,制定、执行和评价货币政策的重要分析工具[8]。
由此看来,当代应用宏观经济方法经历了一个由比较强调经济理论和政策分析,如RBC模型的校准方法;到比较强调样本数据生成机制和模型拟合程度,如VAR模型;进一步到比较强调预测表现、模型比较和政策分析,如贝叶斯VAR模型和DSGE-VAR方法;再到经济理论和数据相结合,模型拟合、预测与政策分析并重(如贝叶斯DSGE模型和DSGE-VAR方法)的发展道路。所使用的宏观经济模型也由确定性模型转变为充分体现经济中不确定性的随机模型,由假定模型就是正确的数据生成过程到充分考虑到模型误设定和灵活性等问题的更为贴近现实的经济模型。在这个过程中,各种理论和方法相互借鉴,也体现了应用宏观经济方法进一步“融合”的趋势。正如Blanchard(2008)指出的,在过去的20年中宏观经济学无论在图景和方法论上都有广泛的“收敛”迹象[9]。
4 贝叶斯估计方法在我国宏观经济建模中的适用性
4.1 宏观经济运行机制和模型设定
我国经济运行正处于由计划经济向市场经济的转轨时期,社会经济结构和国家宏观经济政策的制定和执行也处于不断演化过程中。这种经济的“过渡性”导致了利益分配机制及资源约束条件等的不断变化,也因此导致经济主体的行为很不稳定,宏观经济运行常常大起大落并处于不同的体制区(regime)中。经济主体行为的不稳定使得宏观经济运行的结构参数也很不稳定,常常出现跳跃,并处于不断变化过程中。因此我国宏观经济运行中常常会出现结构断点,宏观经济的数据生成过程和参数出现结构变化。一般经典计量方法都假定经济运行服从一个数据生成过程,结构参数被假定为固定不变的常数,从而使用普通最小二乘(OLS)或传统极大似然方法(MLE)对参数进行估计和统计推断。而我国的宏观经济数据可能不同时期服从不同的数据生成过程和参数结构,因此使用经典计量方法(一般仅假定一个数据生成过程)对我国的宏观经济数据进行的计量分析和统计推断往往是不妥当的,由此得出的宏观经济政策建议往往也是不正确的。而贝叶斯估计方法将模型参数看作是随机变量,并对待估计的模型参数赋予一个先验概率分布,根据贝叶斯定理得出(更新)对模型参数的概率推断。可以看出,贝叶斯估计方法特别适用于像我国这样的转轨经济国家的经济数据建模和政策分析,该方法可以充分考虑经济处于不同体制区的“过渡性”,并能允许经济参数的结构变化。
4.2 宏观经济数据的可获得性和质量
相对于经典估计方法,贝叶斯估计方法对于小样本的估计是更为稳健的(Zeller,1971)。在大样本下贝叶斯估计方法等价于经典估计方法,使用不同先验信息的贝叶斯估计结果的差别在大样本下也将消失。在实证研究中,宏观经济时间序列的数据一般较短(小样本),即使在美国这样宏观经济数据较为丰富的国家也是如此,我国的宏观经济时间序列数据在这方面的矛盾就更为突出(如我国1992年以后才有较完整的主要宏观经济变量的季度数据)。较短的宏观经济数据使得以往运用经典计量方法(如OLS或MLE)估计的中国宏观经济模型往往是不稳健的,而贝叶斯方法能很好地解决我国宏观经济时间序列较短的问题。另外,贝叶斯估计方法使我们可以结合许多国内微观计量研究的成果及其他宏观研究文献(可作为先验信息),对模型进行估计、推断和评价,并获得更为稳健的计量估计结果。而且,我国的宏观经济数据存在统计口径不一致和相当程度的测量误差,贝叶斯估计方法则可将这些误差看作随机扰动,并赋予一定的先验信息结构,从而在一定程度上克服我国宏观经济数据的口径不一致和测量误差问题。综上所述,贝叶斯估计方法非常适合我国转轨经济的特征,可以很好地解决我国宏观经济数据的可获得性和质量等问题。该方法将成为我国宏观经济建模和估计,中央银行制定和执行货币政策的有力工具。
5 结论
本文回顾了应用宏观经济学的主要方法和新进展后认为:现有校准、向量自回归、一般矩方法和极大似然估计等方法都存在诸多缺点,而贝叶斯分析框架的引入能有效地应对这些问题。贝叶斯分析框架是宏观经济学从更为现实的微观基础出发,充分考虑到模型不确定性和结构变化,以更为切实可行的政策分析为目标取得的重大方法论进展。该方法能很好地将理论与数据、微观文献和宏观研究相结合,能很好地解决DSGE模型估计中的识别和误设定问题,而且很适合进行模型的比较和宏观经济政策分析。由于我国宏观经济体制和结构的特殊性及宏观经济数据的特点,贝叶斯方法将在我国宏观经济建模和预测,中央银行制定和执行货币政策过程中发挥重要作用。
[1]Adjemian S.,M.Darracq Paries.Assessing the international spillovers between the US and the euro area:evidence from a two-country DSGE-VAR[Z].Working Paper,European Central Bank,January 2008.
[2]An,Sungbae,and Frank Schorfheide.Bayesian Analysis of DSGE Models[J].Econometric Reviews,2007,26(24):113–72.
[3]Blanchard Olivier J.The State of Macro[Z].NBER Working Paper,14259,2008.
[4]Canova,Fabio.Methods for Applied Macroeconomic Research[M].NJ:Princeton University Press,2007.
[5]Canova,Fabio,Luca Gambetti,and Evi Pappa.The Structural Dynamics of US Output and Inflation:What Explains the Changes[J].Journal of Money,Credit,and Banking,2008.
[6]Cogley,Timothy,and Thomas J.Sargent.Evolving Post- World War II U.S.Inflation Dynamics[C]//NBER Macroeconomic Annual,2001.
[7]Cogley,Timothy,and Thomas J.Sargent.Drifts and Volatilities:Monetary Policy and Outcomes in the Post WWII U.S.[J].Review of Economic Dynamics,2005(8):262-302.
[8]DeJong,David N.,Beth F.Ingram,and Charles H.Whiteman.A Bayesian Approach to Dynamic Macroeconomics[J].Journal of Econometrics,2000(98):203-223.
[9]Del Negro,Marco and Frank Schorfheide.Priors From General Equilibrium Models for VARs[J].International Economic Review,2004(45):643-673.
