用“比较”触发学生的数学思维

■魏 芳

数学是思维的体操，数学思想和方法的学习是数学的灵魂。数学学习就是根据教学内容，引导学生学会比较、归纳、概括、迁移等方法的过程。数学基础知识的掌握，基本技能的形成，基本思想方法的确立，基本活动经验的积累，都是通过对同一系统以及不同系统内知识、方法、思想等进行比较而获得的。

聚焦“比较”，理性解读

顺应学情，从已有经验出发 学习的主体是学生，在组织学生对所学内容和思想方法进行比较时，就要顺应他们已有的认知经验，从他们的已有经验出发组织比较活动。首先要考虑学生的已有知识结构，其次要考虑学生原有的认知习惯与方式。

因势利导，向最近发展区迈进 数学学习是基于学生，又高于学生原有认知水平的思维活动，具有很强的挑战性。在组织比较活动时，需要根据学生的思维特点和认知能力进行针对性的比较，突出知识本质与思想内涵。

螺旋上升，凝炼思想内涵 数学学习的过程是由易到难、由此及彼、纵横相连的。组织学生进行比较活动时，也要遵循知识发生发展的规律，引导学生从对知识的表面解读走向更深层次的理解。使数学概念由模糊走向清晰，由浅入深地发展；使数学方法由单一走向多维，由繁到简地概括；使数学思想由内隐走向外显，由无到有地梳理。

掌握思维的钥匙

在节点处“比”，凸显知识的本质内涵 每一个数学知识都具有独特的本质内涵，在知识形成的关键点处组织恰当的比较，不仅可以凸显知识的特征，而且也能够正确区分相近意义或相反意义的知识。例如，在学习“三角形的分类”，组织学生观察比较：

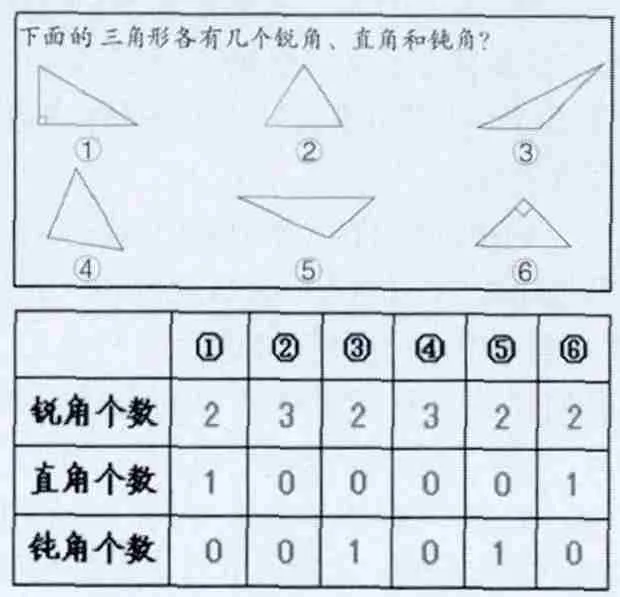
比较一：哪几个三角形可以分成一类，为什么？

学生通过观察，归纳出：

②和④为一类，因为它们的3个角都是锐角，没有直角和钝角。（锐角三角形）

①和⑥为一类，因为它们都有2个锐角，1个直角。（直角三角形）

③和⑤为一类，因为它们都有2个锐角，1个钝角。（钝角三角形）

比较二：每一个三角形至少有几个锐角？

归纳：任意一个三角形至少有2 个锐角，像直角三角形和钝角三角形都有2个锐角，而锐角三角形有3个锐角。

比较三：把所有三角形看作一个整体，这三类三角形都是整体的一部分，它们之间有什么关系？用喜欢的方式表示出来。

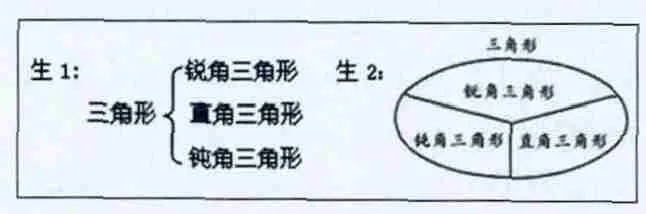
归纳：三角形根据角的特征分成三类，分别是锐角三角形、直角三角形、钝角三角形。

在这一过程中，首先组织学生紧紧围绕“角的特点”进行观察比较和分类归纳，发现三类三角形的不同之处，重在求异；接着组织学生进一步地比较，发现它们之间的共性之处，重在求同；最后组织学生讨论它们之间的关系，重在整体的关系。这样的比较，具有多重意义，既求同也求异，还关注整体之间的联系，有效地凸显了知识的内在本质。

在沟通中“比”，形成知识结构体系 每一个数学知识都处于承前启后的地位，既是在先前知识的基础上发展起来的，又是新知识后续发展的起点。巧用“比较”的策略，对相关知识进行梳理沟通，使学生始终带着结构性的眼光审视知识之间的联系，把握知识之间的结构体系。

在反思中“比”，积累数学活动经验 数学活动经验的积累伴随着数学知识的建构、思想方法的形成过程。反思也是最重要的数学活动，它是数学活动的核心和动力。在数学学习活动之后，组织学生进行及时有效的比较反思，不仅可以及时回顾学习的过程，探索“知识之源”；同时也可以积累相应的学习经验，理解“经验之源”。这样的学习是才有意义的，有深度的。正如著名教育家佐藤学所说：“我们寻求的不是传授教科书知识的效率，而是丰富每一个学生学习经验的效率。”

比较，是一种方法也是一种过程。比较是数学学习的重要方法，数学知识的脉络在比较中逐渐清晰，建构体系；数学技能的要点在比较中不断明确，形成方法；数学思想的本质在比较中逐层凸显，串成规律；数学活动的经验在比较中积淀丰富，内化提升。比较也是数学学习的重要过程，比较的过程正是学生发现问题、提出问题和解决问题的过程，只有真正经历了比较的过程，学生的眼光才会更敏锐，思考才会更全面，经验也会更丰富。巧旋“比较”这把钥匙，会让数学学习充满灵动的魅力，也会让学生的思维走向更为广阔的天地。