应用再循环测度法对城市生态网模型优化

马寨璞 ，吴仑 ，孙斌 ，安秋丹,2

(1.河北大学 生命科学学院，河北 保定 071002；2.国际生态安全合作组织 北京代表处，北京 100600)

在构建城市生态网模型时，需要确定模型的状态变量及个数，借助回归方法得到的状态变量映射关系，可能存在不足或冗余.状态变量和映射关系越多，模型越复杂，模型拟合可能更真实；但超过一定范围后，过多的状态变量或者映射关系，只会使模型过度复杂化，增加模型的不稳定性，并不能提供更多的准确性[1].因此，合理优化状态变量及映射关系的数量在构建复杂生态网模型时不可或缺.

常用于选择、优化模型状态变量的方法有AIC准则[2-5]、BIC准则[2-4]、均方误差最小准则[3]、平均残差平方和统计量(RMSq)准则[4]、Cp统计量准则[3-5]等.它们主要应用于对状态变量个数的筛选[4,7-8]，但不适合于对状态变量映射关系的优化.再循环测度[1]是一种基于连通性指标选择模型结构的标准，主要用来测定生态网络模型中变量间的连通性和循环程度.本文基于再循环测度，对城市生态网模型的映射关系进行优化，从而更为精确地得到了生态网模型中变量之间的关系，探索了城市生态网模型，为网络模型映射关系的优化提供了方法与思路.

1 数据材料

本文以文献[10]中建立的生态网模型为具体对象，该模型对自然、经济、社会3大子系统指标进行了筛选，选取了21个具代表性城市的26项指标.表1中给出了城市生态网模型的各项指标，即模型中的各状态变量.

表1 城市生态网模型选定的指标

2 再循环测度方法原理

在城市生态网模型中，状态变量间建立联系，构成映射关系，一系列状态变量之间的映射，构成了各变量之间的连通或循环.再循环测度[1]通过计算模型中变量间的连通性和循环程度，来说明模型结构的优劣.设状态变量(节点)之间的相互映射用邻接矩阵A表示，各节点之间存在k阶多步连接时，变量之间的映射用Ak来表示.Bosserman定义再循环测度C为幂级数，最初的N个矩阵中1的数目除以N3，它表示总的可能的1的数目，公式(1)给出了再循环测度C的具体计算方法[1]，一般地，再循环测度C值介于0和1之间.

C=A1+A2+A3+…+Ak.

(1)

对于已建成的生态网模型，增加模型中的映射关系，再循环测度值随之呈现增大的趋势.当映射增加到一定程度时，再循环测度C值的增加逐渐趋于缓慢，意味着模型对映射关系不再灵敏，映射处于冗余状态，其判别原理类似于AIC原则.

3 优化独立生态网模型结构

3.1 初始模型的再循环测度

图1是二线、三线城市生态网的映射关系，图中26个节点分别对应选定的26项城市指标，其中实线为原始模型的映射关系，虚线为优化后填补的映射关系.

a b

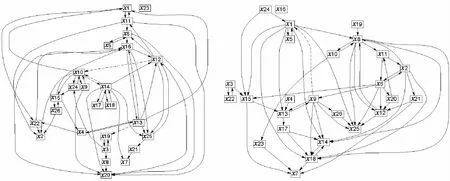
a.二线城市；b.三线城市.图1 二线、三线城市生态网模型映射关系 Fig.1 Mapping relationships for the second-tier and third-tier cities

根据图1，分别计算原始模型的再循环测度，可知二线城市生态网再循环测度值C为0.418 013，三线城市生态网的再循环测度值C为0.362 142.从数据来看，这两类城市状态变量之间的再循环测度值都偏小，表明这两类城市的生态网结构还比较松散.造成这种松散的原因，可能是由于计算使用的统计数据与实际状况相比，一些潜在的映射关系尚未考虑进来.基于此，在原有网络中，可添加适度的映射关系来优化网络结构.

3.2 增加映射关系

在模型中，由于映射关系代表状态变量之间的相互作用，添加应仔细考量.在增加映射关系时，遵循如下原则：1) 优先考虑重要度高的节点作为候选；2) 根据实际研究情况，若在其中发现有潜在映射关系，则可作为补充项；3) 最终，按照对再循环测度值影响由大到小的顺序进行映射的填补.

首先计算重要度，计算时着重综合考虑了节点在网络传输中所起的作用、节点度值和相邻节点的重要度贡献[10].二线城市重要度值最高的5个节点是x10，x14，x13，x3，x24，对应的重要度值分别为0.058 2，0.055 5，0.053 5，0.049 7，0.046 5；三线城市重要度值最高的5个节点是x1，x6，x2，x8，x12，对应的重要度值分别为0.202 3，0.179 0，0.176 3，0.172 7，0.142 1.

对确定的重要节点，综合文献对它们映射关系的研究，再对比回归结果，增补必要的映射关系.为了观察再循环测度值的变化过程，映射关系填补顺序如下：

二线城市：x12→x10[11]，x10↔x14[12]，x13→x19[13]，x18→x10[14]，x10→x13[15-16]，x17→x19[17]；

三线城市：x9→x1[18]，x12→x1[19]，x9→x6[20-22]，x9→x2[23]，x12→x2[19]，x12→x11[24].

3.3 根据再循环测度分析优化方案

为了考察再循环测度的具体变化，逐一计算了添加映射后的生态网模型C值，计算结果见表2、表3.在表中，以M表示模型，上标(2)，(3)分别表示二线、三线城市，下标0表示原始模型，下标中的非0值表示逐步添加映射关系后的模型序号，具体添加的映射关系在每个模型下已给出.

表2 二线城市依次填补映射后模型的再循环测度C

表3 三线城市依次填补映射后模型的再循环测度C

a. 二线城市 ；b. 三线城市.图2 二、三线城市修订模型的再循环测度趋势 Fig.2 Trend of value C for the second-tier and third-tier cities

对比添加映射前后的再循环测度值的变化，可知, 原始的二线、三线城市生态网模型均存在变量间映射关系的缺失.

4 对各类城市整体生态网模型结构的优化

4.1 整体生态网模型再循环测度

上述讨论，分别就二、三线城市生态网模型的再循环测度进行了探讨，为了考虑整体城市生态网模型的结构，选取已定的26个状态变量，将包含一、二、三线城市的数据作为一个整体，样本含量21个，回归得到整体生态网模型如图3，图中实线和虚线共同构成了该原始模型全部映射关系.

图3 各类城市构成的整体生态网模型映射关系 Fig.3 Mapping relationships for all categories of cities

以图3为基础，经计算，其再循环测度值C为0.816 511，再循环测度值偏大，生态网中映射关系应该存在冗余.为了使模型结构优化，需要对冗余映射关系进行适当删减.

4.2 根据再循环测度删减映射关系

在多元回归中，标准化回归系数β绝对值的大小，可以表达一个变量对另一个变量的影响程度[25].同一个模型中，映射关系的相对重要性，也可借助无量纲化的标准回归系数β来权衡.因此，以β值作为删减映射关系的标准.

为了观察再循环测度值的变化，在删除映射关系时，将所有变量之间交互影响的有效β，按照其绝对值从小到大排序，然后从绝对值最小的β所代表的映射关系开始，逐一进行删除.之所以首先从β绝对值最小的映射关系开始，是因为它们在所有映射关系中影响力最小，删减后得到新的模型结构仍然最接近于上一步.计算每一步删除后的再循环测度值，观察其变化趋势(图4)，整体计算结果参见表4.可知，有17条映射关系可以删除，在图3中以带标号的虚线表示，其标号为删除顺序.

图4 删除映射关系后模型的再循环测度值变化 Fig.4 Variation of value C after removing relationships

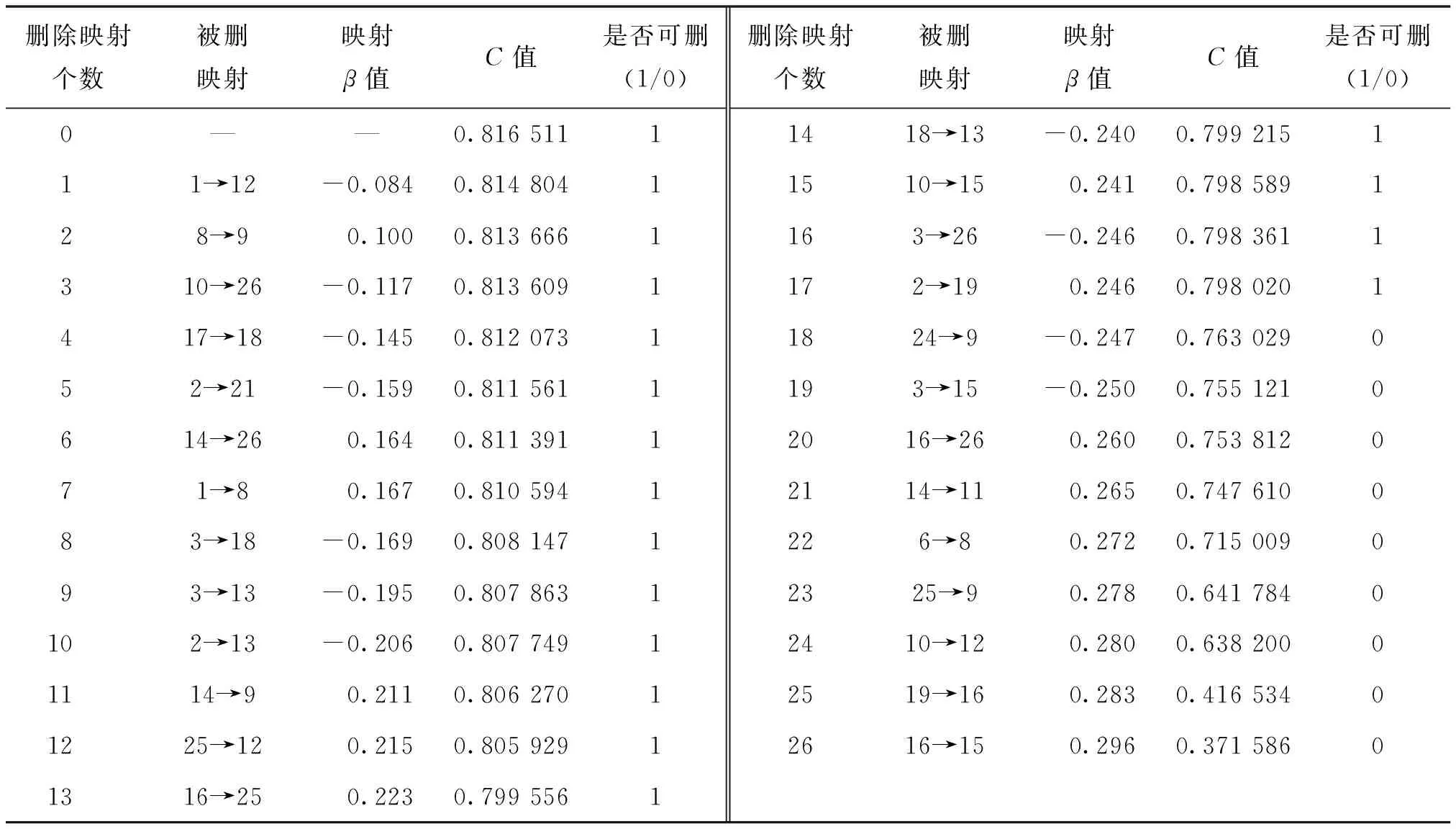
删除映射个数被删映射映射β值C值是否可删(1/0)删除映射个数被删映射映射β值C值是否可删(1/0)0——0.816 51111418→13-0.2400.799 215111→12-0.0840.814 80411510→150.2410.798 589128→90.1000.813 6661163→26-0.2460.798 3611310→26-0.1170.813 6091172→190.2460.798 0201417→18-0.1450.812 07311824→9-0.2470.763 029052→21-0.1590.811 5611193→15-0.2500.755 1210614→260.1640.811 39112016→260.2600.753 812071→80.1670.810 59412114→110.2650.747 610083→18-0.1690.808 1471226→80.2720.715 009093→13-0.1950.807 86312325→90.2780.641 7840102→13-0.2060.807 74912410→120.2800.638 20001114→90.2110.806 27012519→160.2830.416 53401225→120.2150.805 92912616→150.2960.371 58601316→250.2230.799 5561

图4表明，随着删除的增加，再循环测度值C总体呈下降趋势，前17条映射的删除对C值变化幅度影响甚微，直至删除18条映射时，C值开始发生较为明显的变化，减小的幅度开始变大.这说明如果删除18条或更多的映射，模型结构则会受到较大影响，是不能准确描述生态网整体结构的；删除17条映射时，C值达到最佳，删除映射对生态网结构的影响可以忽略.删减后的映射关系参见图3中的实线部分.

结果表明，在城市整体生态网模型中，删除β值绝对值最小的前17项映射关系，可以使生态网模型结构得以优化，具有更简明、准确的结构，此时模型中共计65条映射关系.

同样一批数据，分别作为样本探讨二线、三线城市时，表现为需要增加映射关系，其原因主要是所选样本中的数据尚不能包含所有城市的情况，个别实际因素未能体现在数据中.当一、二、三线城市数据混合在一起，整体考查时，则表现出需要删减映射关系，其原因可能为本次计算中各线城市的数据多寡不均所造成.由于大小城市依其发展水平与地理环境等特点所拥有的生态网结构本身并不相同，也说明相比二、三线城市，后融入的一线城市的结构可能更加复杂、冗余.

5 结论

城市生态系统中，各个指标之间相互作用，构成了理论上的城市生态网，本文以选定的21个城市为调查样本，以选出的26项指标为具体节点，对构建的城市生态网络模型中映射关系的优化进行讨论，主要得到如下结论：

1)二线城市生态网再循环测度值C为0.418，三线城市生态网的再循环测度值C为0.362，两类城市独立生态网模型中状态变量之间的再循环测度值都偏小.综合生态网模型再循环测度值C为0.817，再循环测度值偏大.

3)综合城市生态网模型因其结构的复杂性，存在映射关系冗余现象, 通过对17条冗余映射关系的删减，生态网模型的映射关系达到最优，最适个数为65.

参 考 文 献:

[1] JORGENSEN S E，BENDORICCHIO G.生态模型基础[M]. 何文珊, 陆健健, 张修峰,译.北京：高等教育出版社,2008:32-44.

[2] 王振龙, 胡永宏. 应用时间序列分析[M]. 北京：科学出版社, 2007:96-97.

[3] 数学辞海编辑委员会.数学辞海：第五卷[M]. 北京：中国科学技术出版社, 2002.

[4] 马国栋, 石磊. 线性模型回归自变量选择问题的计算[J]. 云南大学学报：自然科学版, 2005, 27(5A):634-636.

MA Guodong, SHI Lei. Calculate choice of the independent variable of the linear regression model[J]. Journal of Yunnan University: Natural Science Edition, 2005, 27(5A):634-636.

[5] 秦宣云. 基于AIC准则的最近邻聚类模型的优化算法[J]. 系统工程与电子技术,2005,27(2):257-259.

QIN Xuanyun. Nearest neighbor clustering algorithm based on AIC criterion[J]. Systems Engineering and Electronics, 2005,27(2):257-259.

[6] 周婉枝, 陈宇丹. 基于Cp统计量的自变量选择原则[J]. 广西科学, 1995, 2(4):17-18.

ZHOU Wanzhi, CHEN Yudan. The independent variable selection rule based on theCPstatistics[J]. Guangxi Sciences, 1995, 2(4):17-18.

[7] 张辉, 袁兴伟, 程家骅. 东海区小黄鱼繁殖模型优化选择及其管理应用研究[J]. 中国水产科学,2010,17(6):1300-1308.

ZHANG Hui, YUAN Xingwei, CHENG Jiahua. Optimizing selection and application of reproduction model of small yellow croaker in the East China Sea[J]. Journal of Fishery Sciences of China, 2010,17(6):1300-1308.

[8] 王辉, 包默阳.Cp准则应用于遴选最佳ANOVA模型[J]. 哲里木畜牧学院学报,1997,7(4):7-10.

WANG Hui, BAO Moyang. Application of theCPcriterion to selecting best ANOVA model[J]. Journal of Zhelimu Animal Husbandry College,1997,7(4):7-10.

[9] 马寨璞, 安秋丹, 刘庆朝. 城市生态系统指标相互影响的定量研究[J]. 河北大学学报：自然科学版,2013,33(1):68-76.

MA Zhaipu, AN Qiudan, LIU Qingzhao. Quantitative study of indicator interactions in urban ecological system[J]. Journal of Hebei University：Natural Science Edition,2013,33(1):68-76.

[10] 李鹏翔, 任玉晴, 席酉民. 网络节点(集)重要性的一种度量指标[J]. 系统工程,2004,22(4):13-20.

LI Pengxiang, REN Yuqing, XI Youmin. An importance measure of actors(set) within a network[J]. Systems Engineering, 2004,22(4):13-20.

[11] 何薇. 我国第三产业发展区域差异问题研究[D]. 重庆：重庆大学,2007:34-35,45-46.

[12] 袁红霞. 中国城市化与第三产业的相关关系研究[D]. 重庆：重庆大学,2006:32-46.

[13] 李晓晨, 连飞. 从恩格尔系数和收入看我国城乡居民生活差异[J]. 青海统计,2008,2:36-39.

[14] 吴喜雁. 试论人口密度对第三产业发展水平的影响——基于中国的实证研究[J]. 佛山科学技术学院学报：社会科学版,2011,29(3):37-40.

WU Xiyan. The influences of population density on the developmental level of tertiary industry[J]. Journal of Foshan University：Social Science Edition,2011,29(3):37-40.

[15] 杨巧兰, 袁永生, 张立民. 基于协整理论的中国人均收入增长与产业结构变动关系研究[J]. 特区经济,2010,2:263-264.

[16] 黄慧. 城乡居民收入偏低的产业结构原因及调整[J]. 商业文化：财经视点,2011,3:91-92.

[17] 白雪, 王洪卫. 住宅产业综合测度方法研究——基于恩格尔系数与人均住房面积模型分析[J]. 财经研究,2005,31(9):134-144.

BAI Xue, WANG Hongwei. Research on the indexes system in housing industry based on the model of engel coefficient and living space per person[J]. Journal of Finance and Economics, 2005,31(9):134-144.

[18] 周权雄. 政府干预、共同代理与企业污染减排激励——基于二氧化硫排放量省际面板数据的实证检验[J]. 南开经济研究,2009,4:109-130.

ZHOU Quanxiong. Government intervention, common agency and the enterprise’s pollution emission reduction incentive: evidence from the provincial panel data of industrial emissions of SO2[J]. Nankai Economic Studies, 2009,4:109-130.

[19] 聂国卿, 邓柏盛, 尹向飞. 工业废弃物排放与人均GDP之间的关系——以湖南为例[J]. 湖南师范大学：社会科学学报，2010,39(6):101-104.

NIE Guoqing, DENG Bosheng, YIN Xiangfei. The relationship between industrial waste discharge and per capita GDP: a case study of Hunan[J]. Journal of Social Science of Hunan Normal University, 2010,39(6):101-104.

[20] 王曦悦. 固废综合利用寻求突破[J]. 新材料产业,2007,5:2-5.

[21] 龚英. 循环经济中逆向物流的实施现状及发展展望[J]. 铁路采购与物流,2008,3(3):20-22.

[22] 钟明霞. 昆明市工业固体废弃物污染特征与控制对策研究[J]. 环境科学导刊,2007,26(4):45-48.

ZHONG Mingxia. Research on pollution characteristics and control countermeasure of industry solid waste in kunming[J]. Environmental Science Survey, 2007,26(4):45-48.

[23] 艾佳. 我国工业烟尘排放量变化主要影响因素分析——基于SDA的实证研究[J]. 现代商贸工业,2010,22(7):5-7.

[24] 夏凌燕. 2007年广东城镇单位就业与工资情况简析[J]. 珠江经济,2008,203(7):69-73.

[25] 陈峰. 医用多元统计分析方法 [M]. 2版. 北京:中国统计出版社,2007: 30.