区域应急物资储备库选址问题的模糊多目标决策方法

郭子雪, 郭亮, 曾雪梅 , 齐美然

(1.河北大学 管理学院， 河北 保定 071002； 2.河北工业大学 电气工程学院， 天津 300401)

应急物资储备库选址问题是区域应急物资储备体系建设中的重要决策之一，将应急物资储备库置于合理的位置，不仅可以降低成本，而且能够保证提供应急物资的时效性，直接关系到应急物流保障的反应速度和区域应急物资储备体系建设的有效性．目前，国内外学者在应急物资储备库选址方面做了大量的研究工作．文献[1-2]研究了绝对P-Center问题，提出了应急限制期连续条件下的选址模型及其解法；文献[3]通过分析突发事件应急救援设施选址问题的特点，建立了一个多目标决策模型，整合了传统选址模型中常用的最大覆盖模型、P-中心模型和P-中值模型．文献[4]利用集合覆盖理论，通过构建航空应急网络的关系矩阵，研究了航空应急物资储备点选址问题．文献[5]建立了以应急响应时间最小和出救点数目最少为决策目标，带时变供应约束的多出救点选择多目标决策模型．文献[6]针对服务设施经常处于服务状态的情况，在传统的确定性集合覆盖问题模型的基础上，提出了随机条件下的集合覆盖模型；文献[7]提出了基于资源或资金限制的最大覆盖问题(maximal covering location problem，MCLP)，该模型研究了如何使最大数量的人口被覆盖到，并将该模型应用到西班牙Leon省的救护车基地选址中．文献[8]在传统的确定性选址模型的基础上,提出了随机需求情形下应急设施选址问题的风险最小化决策模型，并设计了模型的求解算法；文献[9]建立了应急设施选址问题的2阶段随机混合整数规划模型，提出了模型求解的启发式算法．本文在现有研究基础上，构建了约束条件中含梯形模糊参数的应急物资储备库选址问题的模糊多目标决策模型，给出了模型的有效解法．

1 多目标决策模型

1.1 问题描述

设S1，S2，…，Sn为区域应急物流系统中n个可供选择的应急物资储备库选择点，D1，D2，…，Dm为该应急物流系统的m个应急物资需求点．根据应急管理的特点，假设应急物资储备库选择点到应急物资需求点的行车距离、运输费用、各需求点的需求量以及每个应急物资储备库选择点的容量等系统决策参数均可用梯形模糊数来表示．问在应急物资储备库的容量受限条件下，应如何选择应急物资储备库的位置，才能使该应急物流系统运行总成本和应急物资储备库到达各应急需求点的总距离达到最小？

根据突发事件应急管理的特点，本问题的讨论作如下假设：

1)该问题的目标函数和约束条件都是决策变量的线性关系，且其中的不确定性系统参数均为梯形模糊数形式．2)系统中的应急物资储备库候选点是确定的，每个应急物资储备库候选点的建设成本各不相同，且其应急物资储备具有容量限制．3)突发事件发生后系统中应急需求点的需求量可以预测，各需求点的需求总量小于或等于系统中各应急物资储备库的储备总量．4)考虑到突发事件发生后道路交通状况会受到多种客观因素的影响，从应急物资储备库到应急需求点的运输距离是一模糊变量，用梯形模糊数表示．5)要求各应急需求点由一个应急物资储备库提供应急服务，不考虑应急物资装卸过程中消耗的时间．6)为了兼顾应急物资储备库的可及性以及资金受限条件下资金的利用效率，问题的目标是使应急物资储备库到达应急需求点的总距离、应急系统总的运营成本最小化．

1.2 模型的建立

1)模型参数的涵义

n表示应急物资储备库候选点的个数；m表示应急需求点的个数；i表示应急需求点集数量m的索引号；j表示应急物资储备库候选点集n的索引号；di表示第i个应急需求点的需求量，是一梯形模糊数；sj表示第j个应急物资储备库候选点的容量，是一梯形模糊数；cij表示从第j个应急物资储备库候选点到达第i个应急需求点的运输费用，是一梯形模糊数；fj表示第j个应急物资储备库候选点的固定成本，包括储备库建设费、运营管理费等，是一梯形模糊数；dij表示从第j个应急物资储备库候选点到达第i个应急需求点的运输距离，是一梯形模糊数；xij是0-1决策变量，当需求点i由应急物资储备库候选点j提供服务时它取值为1，否则它取值为0．xj也是0-1决策变量，当应急物资储备库候选点被选中时它取值为1，否则它取值为0．

2)问题的数学模型

基于上述假设，可得应急物资储备库选址问题的模糊多目标规划模型：

(P1): minS=∑nj=1∑mi=1dijxij，

(1)

minC=∑nj=1∑mi=1cijxij+∑nj=1fjxj，

(2)

s．t． ∑nj=1xij=1,i=1,2,…,m，

(3)

xij-xj≤0,i=1,2,…,m；j=1,2,…，n，

(4)

∑mi=1dixij-sjxj≤0,j=1,2,…,n，

(5)

xij,xj∈{0,1},i=1,2,…,m;j=1,2,…,n，

(6)

其中，目标函数(1)是使应急物资储备库到各应急需求点的距离总和达到最小，它表示应急物资储备库对每个应急需求点的有效性；目标函数(2)是使应急系统中应急物资储备库的固定费用与可变费用之和达到最小，它表示所利用资金的使用效率；约束条件(3)表示每个应急需求点仅由一个应急物资储备库提供应急物资；约束条件(4)表示仅对确定设立的应急物资储备库候选点指派需求点；约束条件(5)表示每个应急物资储备库提供应急物资的能力不超过该应急物资储备库的容量限制，同时隐含应急系统储备总量大于等于应急系统总的需求：∑nj=1sj≥∑mi=1dj；约束条件(6)表示决策变量xij,xj均为0-1变量．

2 区域应急物资储备库选址问题的解法

对任意α∈[0,1]， 设梯形模糊数dij,cij,fj,di,sj的截集可表示为

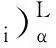
根据区间数的排序规则[10]，约束条件(5)可转化成2个不等约束

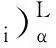
将上述结果代入多目标规划问题(P1)，可得该问题最好的多目标规划问题(P2)

(7)

(8)

s．t． ∑nj=1xij=1,i=1,2,…,m,

(9)

xij-xj≤0,i=1,2,…,m；j=1,2,…，n,

(10)

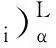
(11)

(12)

xij,xj∈{0,1},i=1,2,…,m;j=1,2,…,n.

(13)

为了确定模糊多目标规划问题(P1)中模糊目标的隶属度函数，现构造2个单目标线性规划问题(P3)和(P4)：

s．t．式(9)—(13).

s．t．式(9)—(13).

令S0,C0分别为规划问题(P3)、(P4)的最优值.

xij-xj≤0,i=1,2,…，m;i=1,2,…，n.

作辅助线性规划问题(P5) 和(P6)：

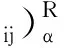
式(9)—(13).

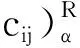
式(9)—(13).

利用单纯形法可以求出线性规划问题(P5)和(P6)的最优解．令S1和S2分别表示线性规划问题(P5) 和 (P6)的最优值，可得模糊多目标规划问题(P1)中目标函数的容许区间：S0≤S≤S1;C0≤C≤C1.

定义模糊多目标规划问题(P1)模糊目标的隶属度函数：

μs(S)=1,S

1-S-S1S0-S1,S0≤S≤S1

0,S>S1，μc(C)=1,C

1-C-C1C0-C1,C0≤C≤C1

0,C>C1.

采用Bellman 和 Zadeh的极小算子，可以将多目标规划问题(P3)转化为单目标线性规划问题(P7)：

(P7): maxβ

s.t.μs≥β

由最佳一致逼近理论可知，该函数具有三个偏差点，即区间的两端点xri-1与xri及区间内某一点.令xzri为区间[xri-1,xri]内幅度相对误差绝对值最大的一点，易知此点误差函数的一阶导数为0.其中，εri为每个区间上幅度相对误差最大值.基于最佳一致逼近理论并结合平方根函数的性质，得出4个方程：

式(9)—(13).

求解模糊多目标规划问题(P1)的具体算法过程如下：

Step 1．写出模糊多目标规划问题(P1)梯形模糊参数dij,cij,fi,di,sj的α-截集.

Step 2． 对于给定的α∈[0,1]，求解线性规划问题 (P3),(P4),(P5),(P6)，得到模糊目标S和C的容许区间[S0,S1]和[C0,C1].

Step 3． 求解多目标规划问题(P2)．采用极小算子将多目标规划问题(P2)转化为线性规划问题(P7)，解之可得模糊多目标规划问题(P1)的α水平最优解．

3 算例分析

假设某区域应急物流系统有5个应急需求点D1,D2,D3,D4,D5和3个应急物资储备库候选点S1,S2,S3．已知从应急物资储备库候选点到各需求点的距离、应急物资储备库候选点的容量限制以及各需求点的需求量如表1所示，应急物资储备库候选点到各需求点的运输费用以及各应急物资储备库的固定成本如表2所示．问如何确定应急物资储备库的位置，才能使该应急物流系统运行总成本和应急物资储备库到达各应急需求点的总距离达到最小？

表1 候选储备库到需求点距离、候选储备库的容量以及需求点的需求量Tab.1 Distance from inventory site to demand point, reserves and demands of emergency material

表2 候选储备库到需求点的运输费用、候选储备库的固定成本Tab.2 Transportation charges from inventory site to demand point and fixed cost of inventory site

取α=0.9，计算梯形模糊数dij,cij,fj,di,sj的α-截集，将计算结果代入单目标规划问题(P3)，(P4)，(P5) 和(P6)，解之可得其最优解如表3所示．

表3 单目标规划问题(P3) (P4) (P5) (P6)的最优解Tab.3 Optimal solutions of single objective programming problem (P3), (P4), (P5) and (P6)

μs(S)=1,S<23.44

1-S-29.295.85,23.44≤S≤29.29,

0,S>29.29μc(C)=1,C<83 781

1-C-101 91918 138,83 781≤C≤101 919

0,C>101 919.

采用极小算子，将多目标规划问题(P3)转化为：

maxβ

s．t． 6.95x11+2.96x21+7.9x31+11.9x41+12.9x51+12.9x12+5.95x22+9.9x32+

7.9x42+5.9x52+15.8x13+9.9x23+12.9x33+1.95x43+3.95x53+5.85β≤29.29,

695x11+296x21+790x31+1 190x41+1 290x51+1 290x12+595x22+990x32+

790x42+590x52+1 580x13+990x23+1 290x33+195x43+395x53+18 138β≤101 919,

x11+x12+x13=1,x21+x22+x23=1,x31+x32+x33=1,x41+x42+x43=1,

x51+x52+x53=1,x11-x1≤0,x21-x1≤0,x31-x1≤0,x41-x1≤0,x51-x1≤0,

x12-x2≤0,x22-x2≤0,x32-x2≤0,x42-x2≤0,x52-x2≤0,x13-x3≤0,

x23-x3≤0,x33-x3≤0,x43-x3≤0,x53-x3≤0,

49.4x11+79.5x21+69.4x31+99x41+79x51-219x1≤0,

49.4x12+79.5x22+69.4x32+99x42+79x52-199x2≤0,

49.4x13+79.5x23+69.4x33+99x43+79x53-248.5x3≤0,

60.5x11+91x21+80.8x31+111.5x41+96.5x41-251x1≤0,

60.5x12+91x22+80.8x32+111.5x42+96.5x52-251.5x2≤0,

60.5x13+91x23+80.8x33+111.5x43+96.5x53-302x3≤0,

xij,xj∈{0,1},fori=1,2,…,5，j=1,2,3.

解之可得上述问题的最优解

β=0.953 8，x11=1，x21=1，x31=1，x43=1，x53=1，x1=1，x3=1，其他为 0．

即该问题的α水平最优解为

x11=1，x21=1，x31=1，x43=1，x53=1，x1=1，x3=1，其他为 0．

计算结果显示，应选择在备择点1，3处设置应急物资储备库，此时目标函数的满意度为95.38%．

4 结论

应急物资储备库选址问题是应急物资储备体系建设的重要内容，研究区域应急物资储备库选址问题对完善区域应急物资储备体系、提高突发事件应对效果具有重要意义．本文基于梯形模糊信息环境，构建了约束条件中含有梯形模糊参数的应急物资储备库选址多目标规划模型，提出了一种基于极小算子的模型优化算法，并通过算例分析验证了该方法的可行性和有效性．

参 考 文 献:

[1] 何建敏，刘春林．应急管理与应急系统--选址、调度与算法[M]．北京:科学出版社，2005.

HE Jianmin, LIU Chunlin． Emergency management and emergency system: Site selection, scheduling and algorithm[M]．Beijing: Science Press, 2005.

[2] 方磊．基于偏好DEA的应急系统选址模型研究[J]．系统工程理论与实践，2006, 8:116-123．

FANG Lei． Research on location model of emergency system based on DEA with preference information[J]． Systems Engineering-Theory & Practice, 2006, 8:116-123．

[3] 陈志宗,尤建新． 重大突发事件应急救援设施选址的多目标决策模型[J]．管理科学，2006，19(40)：10-14．

CHEN Zhizong, YOU Jianxin． A multi-objective decision model of emergency rescue facility location for large-scale emergency incidents [J]． Management Sciences in China, 2006，19(40)：10-14．

[4] 刘浪．基于集合覆盖理论的航空应急物资储备点选址方法[J]．南昌航空大学学报，2010，12(2)：19-26．

LIU Lang． Method of location selection of aviation emergency material depot based on set covering theory [J]． Journal of Nanchang Hangkong University(Social Science), 2010，12(2)：19-26．

[5] 陈达强，刘南．带时变供应约束的多出救点选择多目标决策模型[J]． 自然灾害学报，2010,19(3):94-99．

CHEN Daqiang, LIU Nan． Multi-objective decision mode for multi-depot selection in emergency logistics with time-varying supply volume constraint[J]． Journal of Natural Disasters, 2010,19(3):94-99．

[6] VLADIMIR M, CHARLES R． The queuing probabilistic location set covering and sime extension[J]． Socio-Economic Planning Science, 1994, 28: 167-178．

[7] ADENSO-DIAZ B, RODRIGUEZ F． A simple search heuristic for the MCLP: Application to the location of the ambulance bases in a rural region[J]． Omege, 1997, 25: 81-187．

[8] MUSTAFA S Canbolat, MICHAEL Von Massow．Locating emergency facilities with random demand for risk minimization[J]．Expert Systems with Applications, 2011, 38:10099-10106．

[9] CARMEN G RAWLS, MARK A TURNQUIST．Pre-positioning of emergency supplies for disaster response[J]． Transportation Research Part B, 2010 (44) :521-534．

[10] STEFAN C, DOROTO K． Multiobjective programming in optimization of interval objective functions a generalized approach[J]．European Journal of Operational Research, 1996(94):594-598．