等差分纬线多圆锥投影正解变换的拟合函数模型及误差分析

李 家，肖益松

(1. 辽宁省自然地理与空间信息科学实验室，辽宁 大连 116027； 2. 辽宁师范大学 城市与环境学院，辽宁 大连 116029)

一、投影的基本公式和设计参数

等差分纬线多圆锥投影已在我国编制的各种比例尺的世界地图及其他类型世界地图中得到广泛应用，并获得了较好的效果[1]。由于在ArcGIS、MapInfo、SuperMap等GIS软件中没有该投影的正反解变换功能，在实际工作中只能通过二次开发实现该功能。

根据文献[1]，计算该投影中央经线上x0、y0的公式为

式中，μ0=10 000 000；R=6 371 116 m；φ为要变换的点的纬度值(以弧度计)。

极坐标公式为

式中，(xn,yn)是边缘经线上(Δλ=180°)根据所设计的经、纬线草图所量取的直角坐标值；b=1.1；C=0.000 505 050 5；δφi是某一纬线上各经线的极角；λn是边缘经线与中央经线的经差；λi为各点经线与中央经线的经差(如图1所示)。

计算某一点投影后直角坐标的公式为

文献[1]同时给出了该投影的设计参数，包括直角坐标值(见表1)、纬圈半径ρ和边缘经线上的极角δφi的值(见表2)。

图1 等差分纬线多圆锥投影直角坐标计算示意图

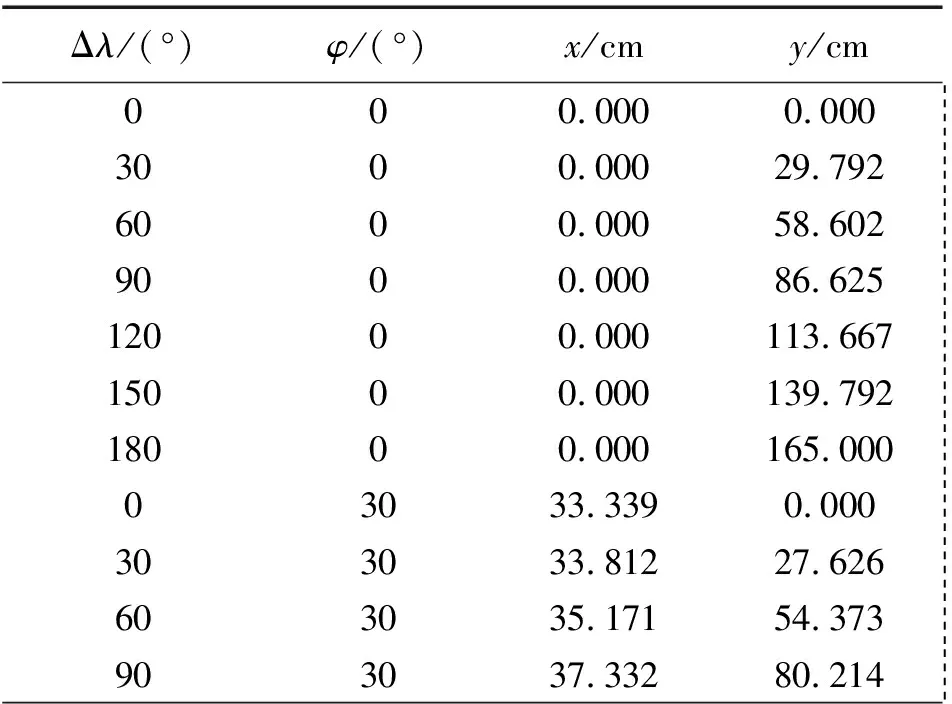
表1 等差分纬线多圆锥投影的直角坐标值

续表

表2等差分纬线多圆锥投影的纬圈半径ρ和边缘经线上的极角δφi的值

φρ/cmδφi10°2399.9433°54′10.5″ 15°1643.3485°38′9.5″ 20°1201.1747°35′46.0″ 回归线1024.1598°47′52.0″ 30°807.63410°51′26.0″ 40°618.06013°29′8.5″ 45°556.62914°31′58.5″ 50°507.56115°24′15.5″ 60°430.76316°39′4.0″ 极圈388.63317°12′31.5″ 70°375.47817°5′27.0″ 75°372.03016°11′0.5″ 80°388.52514°28′57.5″ 90°508.0629°20′42.5″

表1、表2中的数据是基于1∶10 000 000的世界地图的，(x，y)坐标和ρ的单位为厘米。

对地图上某一点从经纬度坐标变换为直角坐标(正解变换)的过程是：根据该点的纬度值和边缘经线的函数式求出该点所在纬线与边缘经线的交点(xn,yn)，这样就可以确定相应的纬圈半径ρ；根据ρ和yn计算交点(xn，yn)的极角δφn(如图1所示)；利用式(2)计算该点的极角δφi；最后利用式(3)计算其直角坐标值。

二、边缘经线的拟合函数模型

国家测绘地理信息局在网上正式发布的世界地图没有给出具体的投影参数和正反解变换公式[2]，因此有些文献提出了各自采用多项式拟合确定边缘经线函数式的方法。

文献[2]从国家测绘地理信息局发布的等差分纬线多圆锥投影的世界地图上选择参考点，采用三次拟合确定边缘经线的函数式

文献[3]根据文献[1]中给出的该投影的设计参数，分析了投影后(x，y)的分布情况，综合考虑精度和计算量，确定x的拟合曲线应为奇次方程，采用一元五次多项式拟合；y的拟合曲线应为偶次方程，采用一元六次多项式拟合

文献[4—5]介绍了苏联中央测绘科学研究所广义多圆锥投影方案(1950年)中的边缘经线的设计函数，其纵坐标x的方程式为纬度的奇次多项式，横坐标y的方程式为纬度的偶次多项式

虽然文献[4—5]中没有指出式(6)可以用于等差分纬线多圆锥投影，但因为等差分纬线多圆锥投影的边缘经线与该方案的边缘经线的对称性质相同，因此可将此拟合函数模型用于等差分纬线多圆锥投影。

分析上述三种边缘经线拟合函数模型可以发现，在式(4)、式(5)基础上通过移轴并考虑到边缘经线的对称性后，可推导得出如下结果

将投影后的直角坐标原点水平移至边缘经线的中点，则去除了常数项，式(7)变为

设x=fx(φ)，根据边缘经线的对称性，有

fx(-φ)=-fx(φ)-a1φ+a2φ2-a3φ3+a4φ4-…=

-a1φ-a2φ2-a3φ3-a4φ4-…a2φ2+a4φ4+…=

-a2φ2-a4φ4+…

因此有

a2φ2=-a2φ2

a4φ4=-a4φ4

……

为使上述等式成立，a2、a4、a6等偶次项的系数只能为0。

同理，设y=fy(φ)，根据边缘经线的对称性，有

fy(-φ)=fy(φ)-b1φ+b2φ2-b3φ3+b4φ4-…=

b1φ+b2φ2+b3φ3+b4φ4+…-b1φ-b3φ3+…=

b1φ+b3φ3+…

因此有

-b1φ=b1φ

-b3φ3=b3φ3

……

为使上述等式成立，b1、b3、b5等奇次项的系数只能为0。这样式(7)就推导成为式(6)。

实际上，即使在边缘经线拟合中不考虑其对称性，采用式(7)这种一般的曲线拟合模型，由于边缘经线上已知点数据本身的对称性，使得解出的待定系数中，a2,a4,a6，…和b1,b3,b5，…的系数也接近于0，表现出了其对称性。但这相当于减少了参与拟合的多项式的项数，因此与使用相同已知点数据和多项式项数但采用式(6)进行边缘经线拟合的结果相比，式(7)的拟合误差明显增大。即使为保证两式的最高次项的方次相近，将式(7)的项数增至式(6)的两倍，式(7)的拟合误差仍大于式(6)。

三、拟合误差对比

在边缘经线的多项式拟合中，一般采用最小二乘拟合，如文献[3]中利用1stOpt软件进行边缘经线多项式拟合。也可以采用分段拟合方法，如文献[6]中选用与投影点的纬度值较近的3～4个已知点进行多项式拟合，这样做虽然在已知点上的拟合误差较小，但因为是分段拟合，边缘经线的连续性稍差。

下面对式(6)和式(7)这两种不同的拟合函数模型进行最小二乘拟合误差对比。程序中采用正规方程组法解出最小二乘拟合后的多项式系数a0,a1,…,aM-1,b0,b1,…,bM-1，根据这些系数确定了式(6)、式(7)的边缘经线多项式，再传入已知点的纬度值求出拟合后的点，计算它与已知点的距离作为拟合误差进行对比。

已知点数据：对表2中的14个点，根据边缘经线对称性，计算出其纬度为负值的对称点，再加上表1中的Δλ为180°、φ为0°的点，共29个点作为已知点。

多项式项数和方次：经过测试，式(6)取5项，项数过多时高次项会导致多项式拟合中的震荡现象，造成投影结果变形。式(7)在两种条件下与式(6)进行对比。第一种条件下两式的项数相同，同为5项。第二种条件下两式的x和y的最高次项方次尽可能相近，测试中x的最高次项的方次可以与式(6)一样取9，而y的最高次项方次与式(6)相同取10时，拟合结果出现震荡现象，因此y的最高次项方次取9次，这样x和y的多项式项数均为10项，为式(6)的二倍，计算时间也相应地增加。

拟合后式(6)的多项式系数为：

a0=1.676 261 862 750 15

a1=-0.000 110 734 568 663 173

a2=1.954 477 061 124 52E-8

a3=-2.668 551 264 636 22E-12

a4=1.344 174 925 330 45E-16

b0=-0.017 050 852 472 941 4

b1=3.941 869 059 706 5E-6

b2=-1.099 928 618 801 22E-9

b3=1.439 009 388 859 4E-13

b4=6.823 147 812 808 01E-18

式(7)取5项时拟合后的多项式系数为：

a0=2.271 571 248 610 32E-14

a1=1.616 105 121 194 76

a2=2.224 643 055 051 45E-17

a3=-4.983 172 137 650 04E-5

a4=2.82518 709 304 736E-21

b0=163.845 946 891 866

b1=-1.469 684 263 135 46E-17

b2=-0.012 379 068 753 132 9

b3=2.030 902 730 958 03E-20

b4=2.952 177 662 935 74E-7

式(7)取10项时拟合后的多项式系数为：

a0=4.745 577 324 584 05E-13

a1=1.673 862 577 481 37

a2=-1.689 756 693 362 57E-15

a3=-0.000 111 052 837 763 137

a4=1.029 503 409 078 15E-18

a5=1.989 551 012 425 34E-8

a6=-2.033 715 263 461 02E-22

a7=-2.650 154 786 566 88E-12

a8=1.251 941 337 157 33E-26

a9=1.269 199 712 877 04E-16

b0=164.593 495 751 958

b1=-9.532 554 139 680 61E-14

b2=-0.014 617 851 141 999

b3=1.618 156 840 527 21E-16

b4=1.418 656 989 887 4E-6

b5=-7.333 870 717 170 98E-20

b6=-1.870 472 805 776 91E-10

b7=1.229 392 976 687 05E-23

b8=9.911 129 417 695 13E-15

b9=-6.829 140 038 805 23E-28

式(7)的两种拟合结果中，纵坐标x的a0、a2等偶次项系数和横坐标y的b1、b3等奇次项系数均近于0，可见关于横轴对称的已知点数据迫使拟合后的多项式对称于横轴。

已知点与对应的拟合后的点之间的距离误差(本文中称拟合误差)见表3。由于式(6)与拟合数据特性相同，也关于横轴对称，而式(7)无此特性，因此表3中式(7)的拟合误差远大于式(6)，其平均值在多项式项数相同条件下是式(6)的9倍，在最高次项方次相近的条件下是式(6)的4倍。

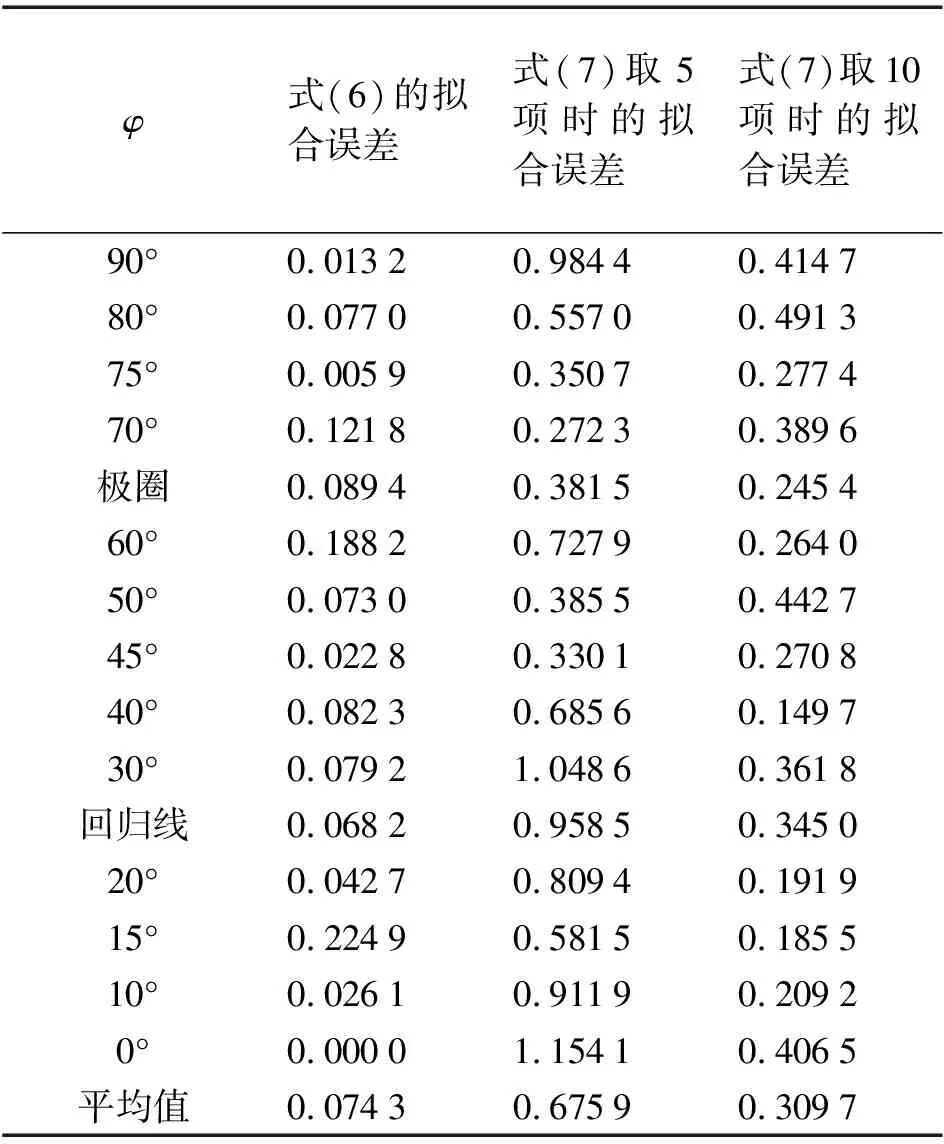
表3 式(6)与式(7)的拟合误差对比 cm

四、结束语

在等差分纬线多圆锥投影正解变换中，边缘经线拟合函数模型的选择对拟合结果影响很大。文献[2—3]中用于另一种广义多圆锥投影的拟合函数模型，考虑到了边缘经线的对称性，因为等差分纬线多圆锥投影的边缘经线具有同样性质，因此应该选用该拟合函数据模型进行正解变换。对比结果表明，这种拟合函数模型与拟合数据的契合度高，因此拟合误差较小。

参考文献：

[1] 胡毓钜，龚剑文，黄伟. 地图投影[M]. 北京：测绘出版社，1981：159-163.

[2] 董曼，李胜乐. 世界地图等差分纬线多圆锥投影的正反解变换[J]. 大地测量与地球动力学，2008，28(2)：95-99.

[3] 叶远智. 栅格数据的等差分纬线多圆锥投影转换[J]. 测绘通报，2012(9)：68-70.

[4] 黄国寿. 地图投影[M]. 北京：测绘出版社，1983：199-201.

[5] 孙达，蒲英霞. 地图投影[M]. 南京：南京大学出版社，2005：119-121.

[6] 李家，赵晴晴. 等差分纬线多圆锥投影正解变换的参数和方法[J]. 地理空间信息，2012，10(2)：38-40.

[7] 国家测绘地理信息局.《世界地图》[EB/OL]. [2013-05-20].https:∥map.sbsm.gov.cn/mcp.

[8] 钟业勋. 不等分经纬线多圆锥投影的设计与解析计算方法[J]. 测绘学报，1965，8(3)：219.

[9] 钟业勋，童新华，李占元. 椭圆边经线多圆锥投影[J]. 测绘工程，2012，21(2)：1-5，8.

[10] 张晓盼，齐欢. 地图投影的最小二乘二元多项式拟合的误差估计[J]. 测绘科学，2003，28(3)：49-51.