红外与可见光图像配准的梯度相关法
2014-08-15胡修兵黄长军
胡修兵,闫 利,黄长军
(武汉大学 测绘学院,湖北 武汉 430079)
一、引 言
利用航空影像制作数字高程模型(DEM)和数字正射影像(DOM)是摄影测量领域已经成熟的技术[1],而机载中波红外DOM的研究还处于起步阶段。由于面阵中波红外相机的分辨率还不高,红外图像的对比度噪声比(CNR)较低[2],因此目前无法直接利用中波红外图像进行摄影测量作业。相对可行的方法是:同时获取中波红外与可见光图像,利用传统摄影测量结果辅助进行红外DOM制作。通过与可见光图像配准,解算红外像点与地面点的精确对应关系,是本文研究的起因。此外,图像配准也是后续将要开展的数据融合和温度场建模等研究的前提。
图像配准主要分为基于区域的和基于特征的两类方法[3]。包括红外与可见光图像在内的多模态图像之间的配准一直是图像配准研究和应用中的难题。由于灰度反差改变的不确定性,在两种图像区域或图像特征之间确立有效的相似性测度都比较困难。在基于区域的方法中,传统的灰度相关方法不适用于多模态图像。源于医学图像处理的互信息方法,是有代表性的多模态图像配准技术[4-5]。互信息利用了图像全局的统计信息,但局部定位能力不足。SIFT是Lowe提出的具有里程碑意义的点特征探测、描述和匹配算子。针对多模态图像,Kelman等提出了SIFT-GM和SIFT-GMEP两种改进算子,多组试验结果说明,当前对于多模态图像特征的一致描述和稳定匹配问题,还有很多困难需要解决。
将梯度信息结合到互信息[6]或单独利用梯度信息进行图像配准已有研究[7],但计算过于复杂,在遥感领域不便于应用。本文将灰度图像转换到复数域的梯度图像,借鉴SAR复数影像配准的相干系数法,提出了一种基于梯度相关性的图像配准相似性测度。其意义明确且形式简单,对中波红外与可见光图像的配准有较好的应用针对性。
二、图像的梯度相关性
如图1所示,红外与可见光图像之间存在明显的灰度特性差异。图像之间的灰度相关性往往随波段距离的增加而减小,灰度反差改变的不确定性也随之增大。红外与可见光图像之间往往会出现不确定的对比度反转,因而无法利用灰度相关方法进行红外与可见光图像的配准。

图1 从相同位置拍摄的中波红外与可见光图像
1. 图像的梯度一致性
图像是物质世界的空间分布在二维平面上的一种映射形式,边缘轮廓的走向是不同模态图像之间几何对应关系的重要线索。若有一对配准的图像,则任意一对同名像点的梯度是一致的,即两梯度向量的无方向夹角为0,或至少有一个梯度的模值为0。
实际图像存在噪声和离散化等误差,而且梯度值较大的位置(边缘、轮廓显著的位置)比梯度较小的位置(平坦区域)为配准提供判据的置信度更高。统计意义上的梯度一致性(以梯度模为权重的梯度夹角平均值趋于0)可以作为多模态图像配准的相似性测度。如果分别计算对应点的梯度夹角和梯度模值[6],每对同名点都要使用反三角函数和三角函数,计算量太大,在遥感领域并不适用。
2. 复数域的向量相关
梯度向量可以用复数表示。图像在实数域的各种灰度相关函数的意义已经被阐明[1],而复数域梯度相关的意义是本文要重点探究的问题。
(1) SAR图像的复相关
SAR图像是复数域的,像点的模值表示雷达回波的能量强度,辐角表示回波的相位。SAR图像的配准判据常采用相关系数[8]
(1)
式中,分子部分为两个复向量组的内积;结果γ为复数;复向量组U1到U2的相关系数与U2到U1的相关系数,互为一对共轭复数。若γ的模为1,表示完全相关,重复轨道的观测期间目标没有任何变化,每对像点的相位差都等于γ的辐角。当各点的相位差不完全相等,则γ的模将小于1,而γ的辐角(笔者认为)即为各点(某种意义上)的平均相位差。
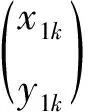
(2)
而各对应点的相位差θk的正切值为
如图2所示,式(2)的意义为:系数γ的辐角θ是每对同名点向量夹角的某种加权意义的平均值,两向量的模乘积越大,这点上的夹角对这个平均值计算权重就越大。
(2) 梯度图像的复相关
由于像点辐角的意义不同,用式(1)直接计算两幅梯度图像的复相关系数,对配准判断并没有意义。理由是:① 配准的多模态图像在对应点上的梯度模值一般并不相等,因此即使是理想配准的多模态梯度图像之间的相关系数模值也不等于1,相关系数的模值大小对梯度图像的配准判断没有意义。② 配准的SAR图像之间可以存在相位差,而理想配准的梯度图像是不应该存在相位差的。如图3所示,像点的梯度方向与像点之间的位置关系是绑定的,不可能出现像点梯度方向一致变化的同时而像点位置关系不变的情况。另外,相位差为0也不能说明两幅梯度图像是配准的。因为如果两幅图像完全无关,则每组对应点的梯度夹角的正负取值概率相等,其相关系数辐角的概率期望值等于0,因此相关系数的辐角也不能直接用于对图像配准的判断。
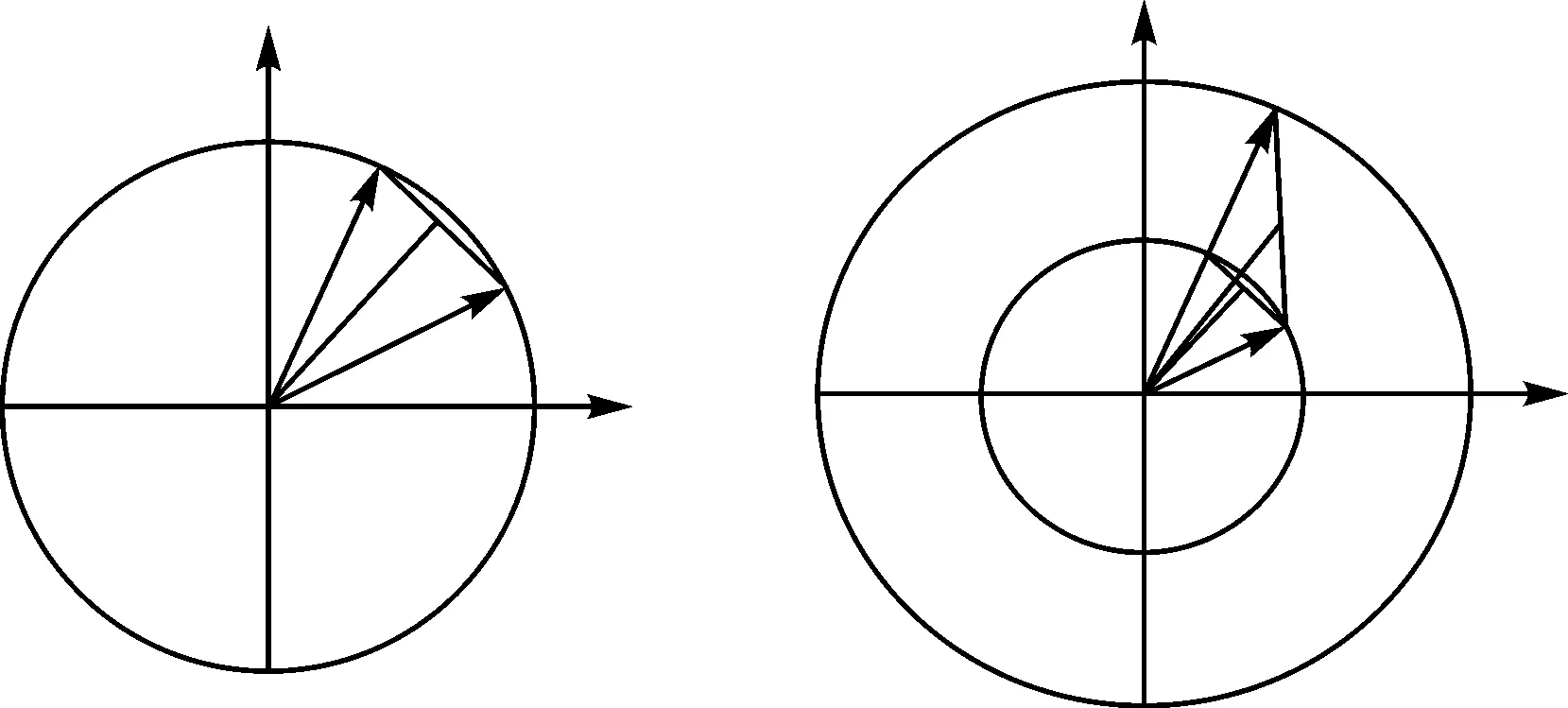
图2 模积加权意义上的辐角平均值
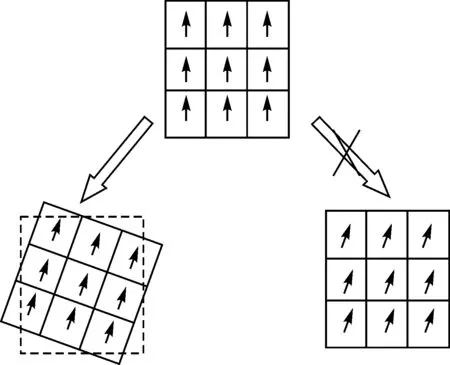
图3 梯度与图像结构的绑定关系
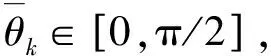
(4)
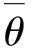
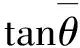
三、试验与分析
1. 整体配准试验
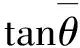

表1 图像整体配准结果

图4 整体配准的局部显示效果
2. 分块配准试验
将图像分成4块(如图5所示),以两个对角块的中心坐标为配准参数,变换图像的旋转和缩放参数由此两点坐标解算。

图5 对角分块配准示意图
对a—b和c—d两组分别优化求解,以对角块中心坐标计算得到最终平移、缩放和旋转参数,见表2。
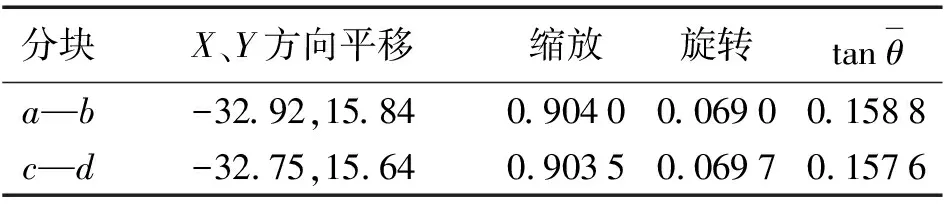
表2 图像分块配准结果
由于红外相机的高精度几何标定场目前还处于筹建阶段,试验用相机未经标定,以上配准试验的精度还不能准确评估。观察表1、表2的结果可以发现,图像之间存在平移量,说明两次拍摄的方向不完全重合。由平移量及红外相机的距焦(25 mm)和像元大小(15 um),可以估算将红外图像纠正到可见光图像相同投影面上时,a—b块与c—d块中心点距离之比约为1.001 2,而表2中缩放率之比为1.000 5。变形方向是符合的,但变形量缩小了。这是由于配准时未考虑图像变形,以整块区域计算“中和”了图像的实际变形量。
3. 配准性能比较
为了检验梯度相关法的局部定位性能,在配准图像中截取25像素×25像素大小的图像块,在配准中心X、Y方向5个像素范围内,以0.1像素为步长,分别按互信息和梯度相关法计算每个位置的配准相似性测度值,测度值分布如图6所示。从图形可以看出,梯度相关法比互信息方法的函数图形更加光顺,有更好的稳定性和局部定位能力。
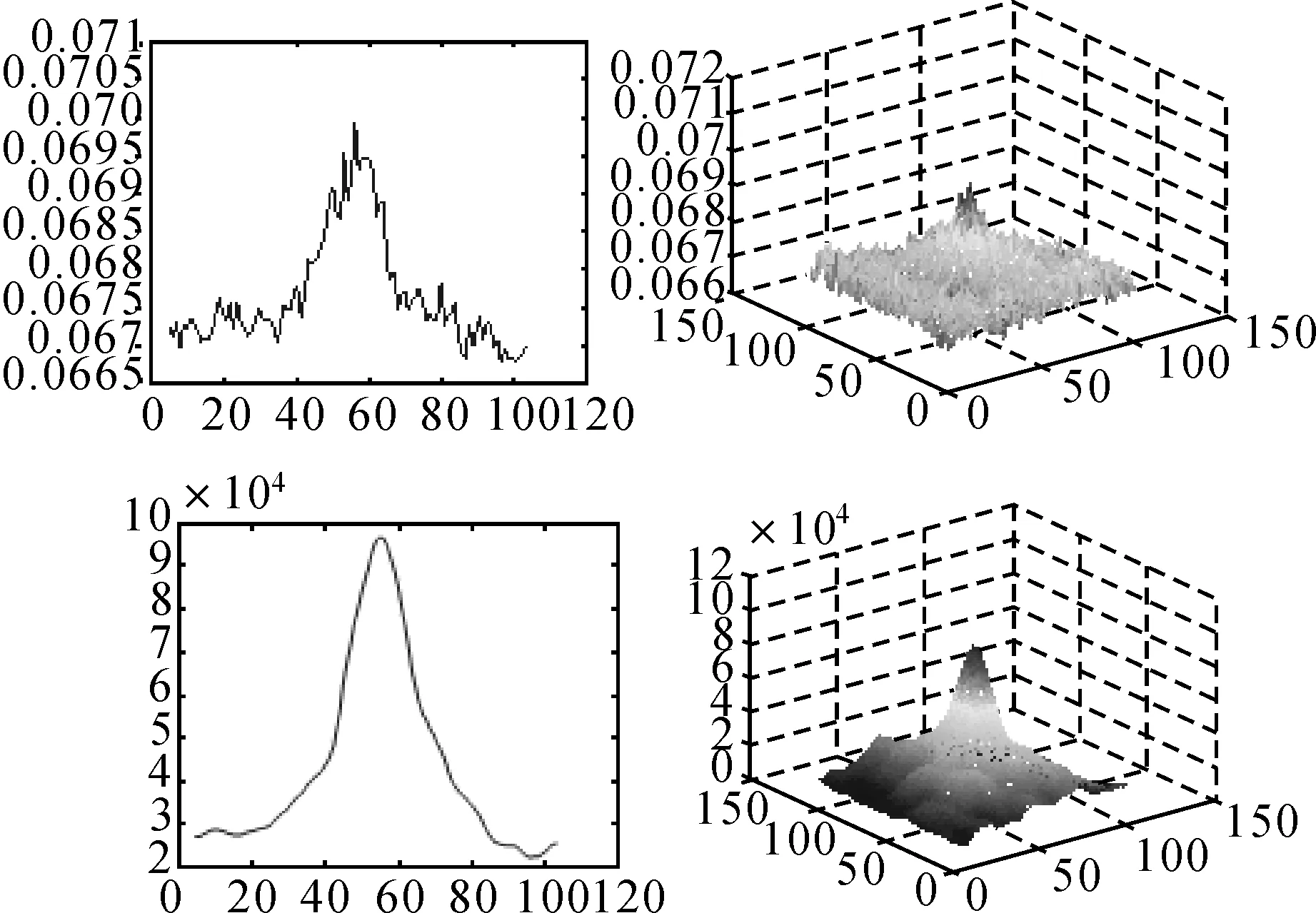
图6 互信息与梯度相关方法的匹配特性比较
四、结束语
利用复数域的图像梯度信息,将传统的图像相关匹配问题从单模态图像推广到多模态图像。由于采用了不同性质的配准相似性测度, 对于多模态图
像的配准问题,梯度相关法可与互信息法互补,或可能发展成为新的替代方法。图像点的梯度具有尺度特性,在相近尺度下的梯度相关性对图像配准判据才更准确。相应尺度下梯度的准确估计和快速计算,是本文方法应用推广的主要技术问题。
参考文献:
[1] 张剑清,潘励,王树根. 摄影测量学[M].武汉: 武汉大学出版社,2009.
[2] LUCKE R L, KESSEL R A. Signal-to-noise Ratio, Contrast-to-noise Ratio, and Exposure Time for Imaging Systems with Photon-limited Noise[J]. Optical Engineering, 2006,45(5):056403.
[3] ZITOVA B,FLUSSER J. Image Registration Methods: A Survey[J]. Image and Vision Computing, 2003,21(11):977-1000.
[4] COLLIGNON A, MAES F, DELAERE D,et al. Automated Multi-modality Image Registration Based on Information Theory[J].Computer and Information Science,1995(3):263-274.
[5] VIOLA P, WELLS W M. Alignment by Maximization of Mutual Information[J]. International Journal of Computer Vision, 1997,24(2):137-154.
[6] ALUIM J P, MAINTZ J B, VIERGEVER M A. Image Registration by Maximization of Combined Mutual Information and Gradient Information[J].IEEE Transactions on Medical Imaging, 2000, 19(8):809-814.
[7] HABER E, MODERSITZKI J. Intensity Gradient Based Registration and Fusion of Multi-modal Images[J]. Methods of Information in Medicine, 2007,46(3):292-299.
[8] 舒宁.雷达影像干涉测量原理[M].武汉:武汉大学出版社,2003.
