基于贝叶斯面板平滑转换模型的房价阈值效应研究*

(湖南大学工商管理学院，湖南 长沙 410082)

基于贝叶斯面板平滑转换模型的房价阈值效应研究*

朱慧明，游万海，李小依

(湖南大学工商管理学院，湖南 长沙 410082)

针对经济变量之间普遍存在的非线性关系，导致线性模型拟合失效的问题，构建面板数据平滑转换模型，刻画变量之间关系的非对称性。采用贝叶斯方法进行模型的参数估计，避免非线性最小二乘算法难以收敛，参数估计不确定。通过分析模型结构，选择参数先验分布，设计相应的Metropolis-Hasting-Gibbs混合抽样算法，据此估计模型参数；在此基础上，利用省域面板数据分析房价阈值效应问题。研究结果表明：参数的动态迭代轨迹收敛，MH-Gibbs混合抽样算法能够准确地估计模型各参数，解决了非线性最小二乘无法收敛的问题，证明了贝叶斯面板数据平滑转换模型的有效性；同时也验证了房价波动的阈值效应以及房价与城市化、城乡收入差距之间的非线性关系。

房价；城市化；面板数据；平滑转换模型；贝叶斯分析

一 引 言

异质性是经济金融变量的主要特征之一，有效地刻画数据的异质性是合理建模的前提。面板数据模型通过引入个体和时间效应，能够有效地刻画个体之间的异质行为特征和揭示经济运行规律，因此，被广泛的应用于描述各种复杂经济社会现象。然而，经济金融变量常表示出非对称和非线性关系，使得经典的线性面板数据模型失效。例如，在资本市场中，由于买方和卖方之间的信息非对称性，个体公司的投资决策通常与其他金融变量相关，如现金流量。面板平滑转换回归模型(Panel Smooth Transition Regression, PSTR)通过引入转移变量使得模型系数具有时变性，不仅可以刻画个体之间的异质性，同时也能有效地描述经济金融变量间的非对称关系，从而被广泛应用于经济、金融、环境和能源领域，探索其内在的行为规律。房地产行业作为国民经济的重要产业，非理性投机需求、单维经济利益驱动推动房价泡沫的形成，房地产市场供需机制畸形引发的金融稳定等问题倍受关注。

伴随城市化进程的不断发展，探究城市化促进房价上涨的方式和作用的大小成为学术界研究的重点。Kottis[1]认为人口从农村向城市的转移对房地产市场的扩张产生了促进作用，引起了房价的上涨。Michaels和Rauch[2]研究了美国人口从农村向城市的转移，认为该转移伴随着机制转换。Gabriel[3]对加利福尼亚州两个最大城市住宅价格的变化模式进行分析后发现，庞大的人口迁移规模是近几十年来加利福尼亚州住宅价格变化的主要因素。Koetter和Poghosyan[4]认为城市化水平是房地产价格的重要环境变量之一。Ghebreegziabiher和Debrezion[5]研究发现，大城市的房价会伴随城市化的进程而有所提高。程开明[6]基于误差修正模型并进行协整分析，认为城市化水平与房地产价格之间存在着长期均衡关系，城市化构成房价的Granger原因。同时也有不少学者研究了城乡收入差距对房地产价格波动存在显著影响。胡晓[7]认为较大的收入差距是构成房价上涨的重要因素。Flaherty[8]认为城乡收入差距拉大对房价具有显著的正向促进作用，Quigley[9]等人的研究同样证实这一观点。陈健和高波[10]构建面板联立方程模型研究发现，收入差距与房价之间存在正向互动关系，收入差距扩大推动房价上涨，房价上涨也会引起收入差距的扩大。以上对房价的研究都是在线性模型的基础上考察了城市化水平、城乡收入差距对房地产价格的影响，并未考虑变量间可能存在的非线性特征。

对变量的非线性特征、变量之间的非线性关系的研究已引起众多学者关注，Hansen[11]利用英国公司15年数据研究了财政限制与投资决策的非线性关系。Lee和Chiu[12]发现了保险金在存在阈值效应。Julien[13]利用面板平滑转换模型研究区域资本流动性，分析了投资与储蓄之间的非线性关系。Rosa和Vicente[14]利用PSTR模型，在环境库茨曲线的理论框架下，研究了人均用水量与人均收入的非线性关系。Jude[15]研究发现经济发展与金融发展的非线性关系。Omay和Kan[16]运用非线性最小二乘法研究出口贸易对通货膨胀的非线性影响的参数。学者骆永民[17]基于平滑转换模型分析城市化对房价的影响，研究发现，我国房价波动表现出明显的非对称性，具有很强的非线性特征。但是非线性最小二乘法(NLS)估计平滑转换模型存在参数估计难以收敛的问题，会导致参数估计不准确。贝叶斯方法将参数的先验信息运用到统计推断中，不仅提高了统计推断的准确性，而且可以解决参数估计不确定等难题。Wang和Holan[18]运用贝叶斯方法估计多机制平滑转换模型参数，有效并且准确地解决模型参数估计不收敛的问题。

本文将构建贝叶斯面板数据平滑转换模型解决线性模型拟合非线性关系失效的问题，设置先验分布，根据贝叶斯定理，得到各参数相应的完全条件后验密度函数，设计MH-Gibbs混合抽样算法估计模型参数，解决参数估计难以收敛问题；并且利用省域面板数据对房价波动的阈值效应进行实证分析。

二 贝叶斯面板数据平滑转换模型构建

(一)模型结构分析

面板数据平滑转换模型不仅可以刻画多个不同个体随时间变化的行为特征，分析各个个体之间的共性与异质性，而且因其参数可以随着一个含有外生变量的函数进行平滑转变，进而模型描述了所有截面个体的参数对应于某一变量具有非线性转换以及转换渐进的行为特征。Gonzalez和Dijk[19]提出面板数据平滑转换模型(PSTR)，该模型是面板数据门限回归(PTR)模型的推广，面板数据平滑转换模型的表达式如下：

yit=αi+β1xit+β2xitg(qit;γ,c)+εit，

i=1,2,…,N;t=1,2,…,T

(1)

其中，yit为被解释变量，i表示面板数据的个体维度，t表示时间维度，β1和β2依次为线性部分和非线性部分的参数向量。αi表示截面个体固定效应，εit为残差项。g(qit,γ,c)是一个取值介于0～1之间、连续的转换函数，可观测变量qit称为转换变量，qit可以是xit向量组成部分的函数，也可以为一个不包含在xit内的外生变量。参数γ为平滑参数，表示从一个机制转换到另一个机制的速度或调整的平滑性，决定了转换的速度。c为发生转换的位置参数，是机制转换发生的临界值，即阈值水平。g(qit;γ,c)常用如下形式的逻辑函数:

(2)

其中，在实际应用中，d通常取1或2。当d=1时，转换函数的形式为LSTR1型，关于转换变量qit单调递增。当g(·)=0时，模型处于低机制；g(·)=1时，模型处于高机制，转换函数值在0和1之间平滑转换，实现模型在两种机制之间平滑转换。当d=2时，转换函数称为LSTR2型，在(c1+c2)/2处，g(·)达到最小值，对应的机制为中间机制。

当γ→，d=1时，，其表达式为：

(3)

此时，g(·)为示性函数I[qit>c]，PSTR模型转化为两机制的PTR模型；当γ→，d=2时，，其表达式为：

(4)

此时，g(·)为示性函数I[c1≤qit≤c2]，PSTR模型转化为包含两个相同机制和一个中间机制的PTR模型；当γ=0时，无论d如何取值，g(·)值均为0，此时PSTR模型退化为线性固定效应模型。因此，线性固定效应模型和PTR模型均为PSTR模型的特殊情形。

(二)贝叶斯分析

对于个体i，面板数据平滑转换模型的矩阵形式为：

(5)

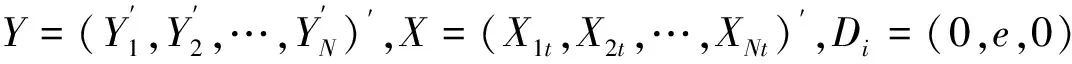
Y=ZΨ+ε，ε～N(0,σ2I)

(6)

给定(γ,c)，Y服从期望为ZΨ，协方差矩阵为σ2I的正态分布，即Y～N(ZΨ,σ2I)，则面板数据平滑转换模型的似然函数为：

L(Y|X,Ψ,γ,c,σ2)∝σ-NT

(7)

由于参数的后验概率密度函数可以通过模型参数的先验分布与模型的联合似然函数的乘积获得，因此要实现对模型的贝叶斯分析，参数先验分布的设置是前提。已知模型的似然函数，设置参数的先验分布，从而可得参数的后验密度函数。根据Lopes和Salazar[20]的观点，模型参数先验分布设置为：

Ψ～N(μΨ0,VΨ0)，σ2～IG(λ0,θ0)，

γ～G(ζ,ϖ)，c～N(μc0,Vc0)

(8)

此处，G为Gamma分布，IG为逆Gamma分布。

根据贝叶斯定理，模型参数的联合后验密度正比于参数的先验分布与模型似然函数的乘积，在不考虑参数先验的相依性的情况下，联合后验分布函数的具体表达式如下：

π(Ψ,γ,c,σ2|Y,X)=π(Ψ,γ,c,σ2)×

L(Y|X,Ψ,γ,c,σ2)/π(Y)

∝L(Y|X,Ψ,γ,c,σ2)π(Ψ)π(γ)π(c)π(σ2)

(9)

由于参数的联合后验分布形式比较复杂，不属于已有统计分布的范畴，无法对其进行直接抽样，因此下文研究讨论各参数的完全条件后验分布，以方便运用MCMC抽样算法进行抽样。

(1)参数Ψ的完全条件后验分布。根据条件概率定义，在给定γ，c和σ2的条件下，参数Ψ的完全条件后验分布密度函数为：

π(Ψ|Y,X;γ,c,σ2)=π(Ψ,γ,c,σ2|Y,X)/

π(γ,c,σ2|Y,X)∝L(Y|X,Ψ,γ,c,σ2)π(Ψ)

(10)

其中

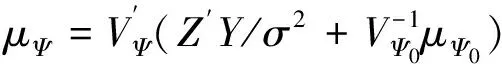
根据Ψ的完全条件后验分布形式，可以知道，Ψ服从期望为μΨ，协方差为VΨ的正态分布。

(2)参数σ2的完全条件后验分布。类似地，σ2的完全条件后验分布密度函数为：

π(σ2|Y,X,Ψ,γ,c)=π(Ψ,γ,c,σ2|Y,X)/π(Ψ,γ,c|Y,X)

∝L(Y|X,Ψ,γ,c,σ2)π(σ2)

∝(σ2)-λ-1exp (-θ/σ2)

(11)

此处，λ=NT/2+λ0，θ=(Y-ZΨ)′(Y-ZΨ)/2+θ0，由σ2的完全条件后验分布形式可知，σ2服从形状参数为λ，尺度参数为θ的逆Gamma分布。

(3)参数γ和c的完全条件后验分布。参数γ和c的完全条件后验分布密度函数形式比较复杂，没有已知的标准统计分布可以用来抽样。因此可以采取随机游走Metropolis-Hasting抽样算法进行联合抽样。设(γ，c)的当前值为(γ(m),c(m))，点(γ*,c*)从建议分布γ*～N(γ(m),Δγ)，c*～N(c(m),Δc)中抽样产生。那么(γ*,c*)的接受概率为：

p=min {1,η}

(12)

其中

此处，Z*=Z(qit;γ*,c*)，dN和dg分别表示密度函数为正态分布和Gamma分布。Δγ和Δc是抽样的调整值，使得接收概率在0.3与0.4之间。

(三)MH-Gibbs混合抽样

根据模型参数Ψ和σ2的完全条件后验分布以及遍历性定理，可以利用基于Gibbs抽样的MCMC数值算法进行模拟仿真；同时Metropolis-Hasting抽样算法对参数(γ,c)进行抽样分析，以获得模型参数的贝叶斯估计及其分位数。贝叶斯面板数据平滑转换模型的MCMC抽样过程如下：

(1)给定各参数的初始值为(Ψ0，γ0，c0,(σ2)0)，假设(Ψ(m),γ(m),c(m),σ2(m))是第m次迭代结果，M为抽样次数。

(2)从(Ψ|Y,X,γ(m),c(m),σ2(m))～N(μΨ,VΨ)中抽取Ψ(m+1)；

(3)从(σ2|Y,X,ψ(m+1),γ(m),c(m))～IG(λ,θ)中抽取σ2(m+1)；

(4)从γ*～g((γ(m))2/Δγ,γ(m)/Δγ)，c*～N(c(m),Δc)中抽取(γ*,c*)，使得：

(5)令m=m+1，重复(2)至(4)，直至收敛。

在抽样初期，参数初始值的设定对随机数的生成影响较大，得到的MC链条非平稳，所以为了保证MH-Gibbs抽样算法的有效性和估计模型参数的准确性，应该去掉最初产生的m个随机数，利用剩余的M-m个数据进行分析。同时，在剩余的链条中，每h个生成数随机抽取一个作为样本集合中的元素，可以减少链条的自相关性，因此，实际用于分析的数据为N=[(M-m)/h]个。Markov链为：(Ψ(m+k+nl),γ(m+k+nl),c(m+k+nl))。那么模型的参数的MC估计为：

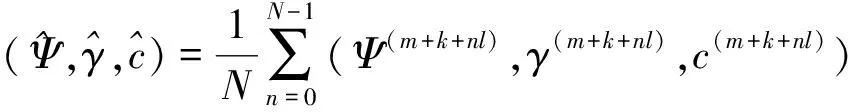
n=0,1,…,N-1，1≤k≤h

(13)

三 实证研究

(一)指标与数据

选取我国31个地区2002～2011年的城市化水平、城乡收入差距与房地产价格的面板数据建立平滑转换模型，研究城市化水平以及城乡收入差距对房地产价格的影响。单位销售面积的销售额即销售额除以销售面积，表示房地产价格(PH)；城市化水平(UR)为城镇人口总数除以总人口数；城乡收入差距(YG)采取城市人均可支配收入与农村纯收入的差；当经济发展水平较高时，一个地区的商业和人口往往比较集中，房价自然也较高，因此选取人均国内生产总值(pGDP)作为转换变量。文中所用数据来源于国家统计局和国泰安数据库。图1分别给出了房地产价格、城乡收入差距以及城市化水平的核密度图。

根据三个变量的核密度图可以知道，房地产价格的核密度波峰持续右偏且波及范围越来越广，这说明房地产平均价格在逐渐上涨且各地区的差距在增大；城乡收入差距的核密度图波峰偏移不是很明显，且波及范围不大；城市化水平核密度呈现明显地双峰特征。这说明三个变量均存在“低状态”和“高状态”两个形态，每个形态都有不同的分布特征，说明城市化水平与城乡收入差距对房地产的价格影响，回归系数在不同形态会呈现不同的特征，这初步验证了面板数据平滑转换模型的适用性。

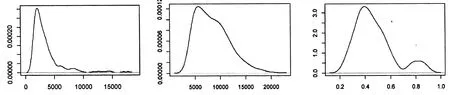
(a)PH核密度图 (b)YG核密度图 (c)UR核密度图

(二)数据分析

在经济面板数据分析中，对非平稳的面板数据进行回归，容易产生伪回归问题，因此对面板数据的平稳性检验是必不可少的步骤之一，其中，单位根检验在检验数据平稳性占有至关重要的作用。因此，首先对各个变量序列进行单位根检验。

常用的单位根检验方法有LLC检验和IPS检验，两种检验方法建立在扰动项独立不同分布、允许异方差的基础上，并且考虑了单个个体扰动项的自相关情形。LLC和IPS检验两种单位根检验方法都基于传统单一时间序列数据的DF和ADF检验式，正如白凡[21]的观点，其不同之处是在个体间独立与同质的不同假定下，采用不同的数据处理方法建立了不同的检验式统计量，证明其收敛于标准正态分布。两种检验方法均采用ADF检验式，表达式为：

(14)

LLC检验假设所有个体在原假设和备择假设下都存在同质性，原假设和备择假设设置如下：

H0:δ1=δ2=…=δN=0；H1:δ1=δ2=…=δN<0

(15)

与LLC检验相比较，IPS检验放松了个体同质性的要求，IPS检验的假设只要求原假设下每个个体具有同质性，允许备择假设中部分个体不同，即部分δi为0，这放松了LLC检验中所有δi都必须相同的约束。IPS检验的原假设和备择假设设置如下：

H0:δ1=δ2=…=δN=0；H1:δ1=δ2=…=δNl<0,

δNl+1=δNl+2=…=δN=0

(16)

IPS检验在同质性要求上的放松，更加符合经济数据的特点，承认整体平稳和个体数据不平稳的事实。单位根检验的原假设H0:存在单位根；H1:不存在单位根。根据Eviews6.0软件进行单位根检验，在95%的置信水平下检验结果如表1。

表1 参数的单位根检验结果

*表示95%的置信水平下显著

根据表1中检验结果，各p值均小于0.05，两种检验方法均拒绝原假设，表示各个变量在个体同质和异质条件下均不存在单位根。做出以下模型：

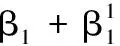
在MH-Gibbs抽样过程，首先对模型中的参数进行100000次抽样，舍弃前10000次结果，每6个生成数随机抽取一个作为样本的元素，构成样本量为15000的Markov链，得到模型参数估计结果。图2-4分别给出了各参数的迭代轨迹图、Geweke检验图以及自相关图。

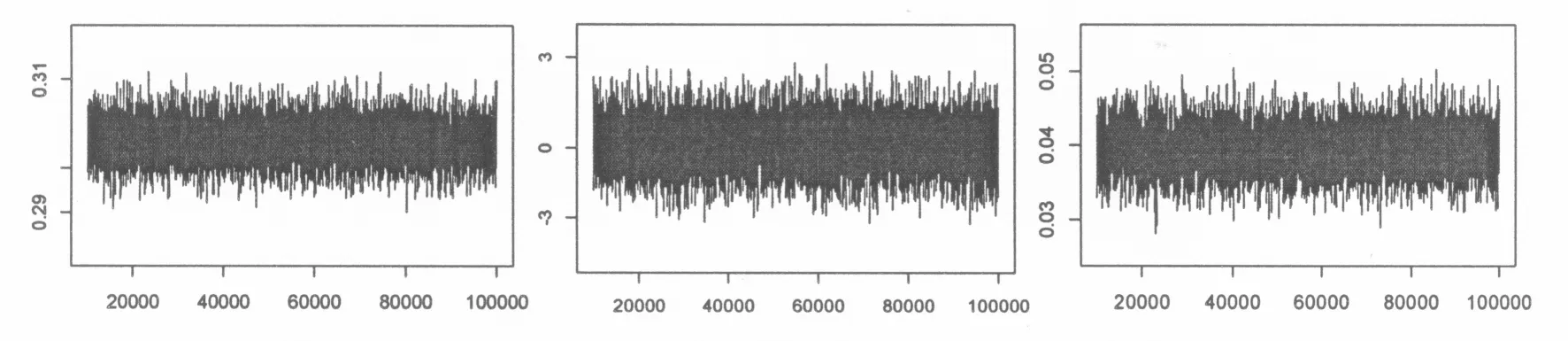
(a)β1迭代轨迹图 (b)β2迭代轨迹图 迭代轨迹图

迭代轨迹图 (e)c迭代轨迹图 (f)γ迭代轨迹图

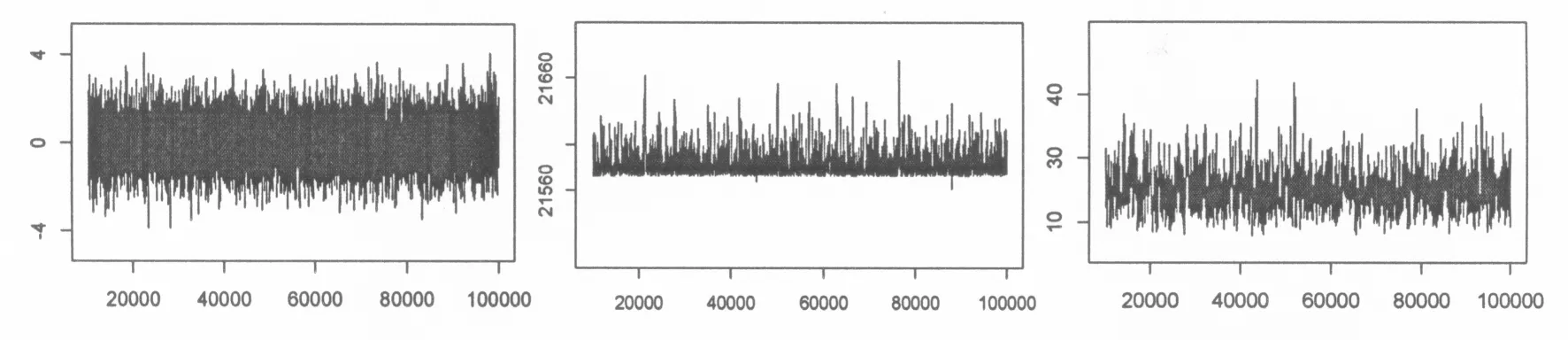
由各参数的动态迭代轨迹图可知，参数的动态迭代轨迹都已达到平稳，稳定地分布在一条水平线附近，没有呈现出明显的周期性和规律性，说明贝叶斯面板数据平滑转换模型主要参数的后验分布都已达到稳定状态，此时抽样得到的数据基本可行，MH-Gibbs混合抽样方法所得样本平稳性较好。但仍需判断抽到的Markov链是否收敛。图3是Geweke收敛检验图。

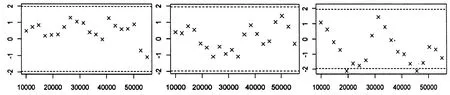
(a)β1收敛检验图 (b)β2收敛检验图 收敛检验图

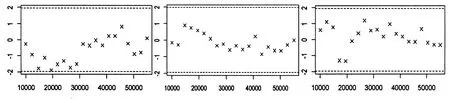
收敛检验图 (e)c收敛检验图 (f)γ收敛检验图

由Geweke检验图可知，各参数的Z统计量的值均处于-1.96和1.96之间，因此可以认为，在95%的置信水平下，迭代初的样本均值与迭代末的样本均值不存在显著性差异，因此可以判断MCMC混合抽样方法得到的Markov链是收敛的。

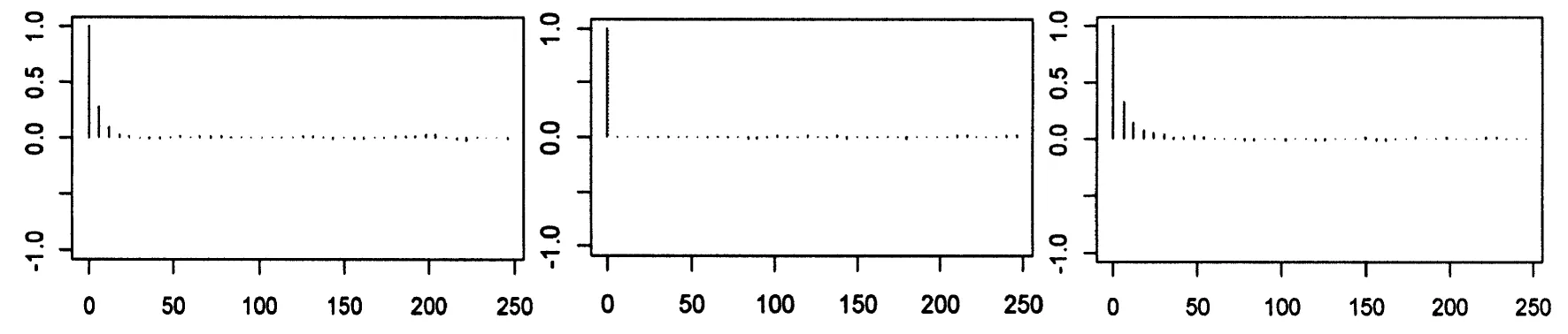
(a)β1自相关图 (b)β2自相关图 自相关图

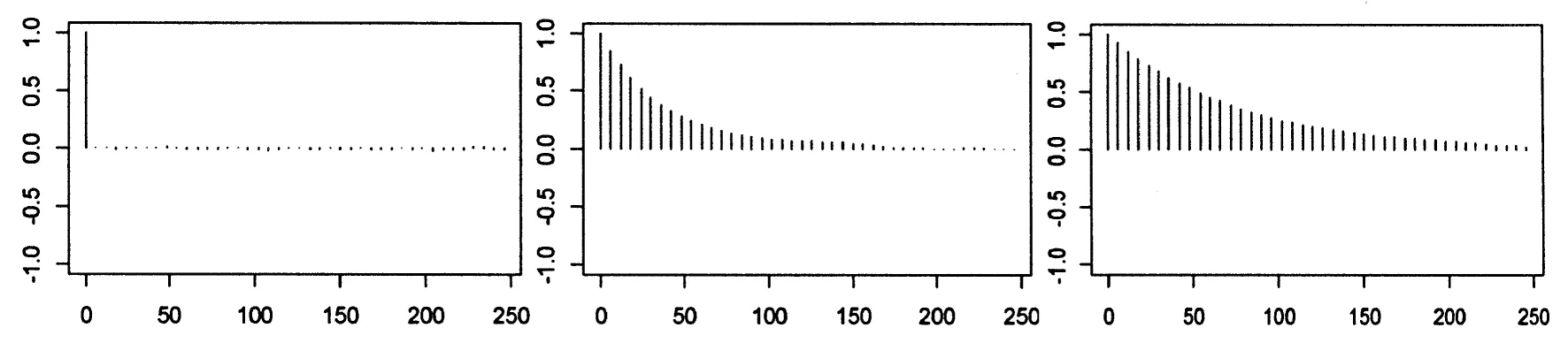
自相关图 (e)c自相关图 (f)γ自相关图

根据参数的自相关图可以知道，初始值不同，参数的自相关系数随着迭代次数的增加逐渐趋近于0，表明各参数不存在自相关。综合模型参数的动态迭代轨迹图，可知得到的抽样数据是有效的。图5是模型参数边缘后验分布核密度。

从各参数的后验密度图可知，除了参数c，其它各参数的边缘后验分布核密度估计曲线都比较平滑，且有明显的单峰对称特征，说明参数贝叶斯估计值误差非常小。虽然参数c的后验分布不服从正态分布，但后验分布图存在单峰特征，也说明参数贝叶斯估计值误差非常小。图5说明了MH-Gibbs混合抽样方法有效地模拟了模型中各参数的边缘后验分布。根据MH-Gibbs抽样结果，结合核密度估计图，可以模拟得出参数的贝叶斯估计值。表3给出了各参数的后验均值估计、标准差、MC误差、2.5%分位数、97.5%分位数的贝叶斯估计值。

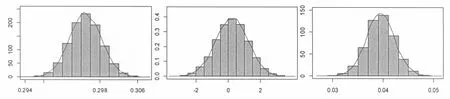
(a)β1后验密度图 (b)β2后验密度图 后验密度图

后验密度图 (e)c后验密度图 (f)γ后验密度图

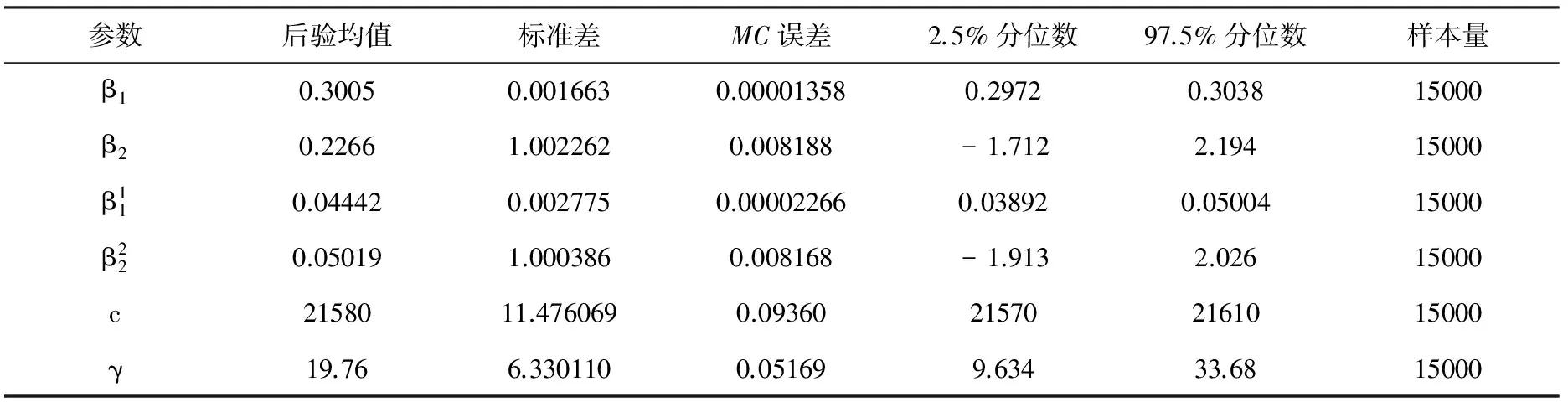
表2 参数的MC估计结果

根据表3各参数的估计结果，可以得出以下分析：

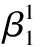
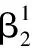
四 结 论

本文针对面板数据平滑转换模型估计算法难以收敛的问题，构建贝叶斯面板数据平滑转换模型，设置先验分布，根据参数的完全条件后验分布信息设计相应的MH-Gibbs混合抽样方案，据此进行模型参数的估计。在此基础上，利用中国省域面板数据研究房价波动的阈值效应。结果发现：模型的各个参数的迭代轨迹均是收敛的，参数估计的MC误差都比较小；并且后验密度曲线为钟形，说明MH-Gibbs混合抽样算法有效地模拟了参数的完全条件后验分布，贝叶斯面板数据平滑转换模型能够更好地说明变量之间的关系，同时也验证了房价波动存在阈值效应。本文运用新的模型研究发现房价波动存在阈值效应，同时也采用贝叶斯方法解决常用参数估计方法不确定性的问题。但是文中只考虑了模型存在两种状态，并未考虑可能存在更多种状态，而且各个个体阈值是相同的，未考虑个体阈值的不同，这也是进一步研究的问题。

[1] Kottis A. Impact of migration on housing in urban areas[J]. The Annals of Regional Science, 1971, 5(1): 117-124.

[2] Michaels G, Rauch F, Redding S J. Urbanization and Structural Transformation[J]. The Quarterly Journal of Economics, 2012, 127(2): 535-586.

[3] Gabriel S, Rosenthal S. Quality of the business environment versus quality of life in a dynamic model of urban composition and growth[J]. The Review of Economics and Statistics, 2003, 86(1): 438-444.

[4] Koetter M, Poghosyan T. Real estate prices and bank stability[J]. Journal of Banking &Finance, 2010, 34(6): 1129-1138.

[5] Ghebreegziabiher D, Pels E, Rietveld P. The Impact of Rail Transport on Real Estate Prices: An Empirical Analysis of the Dutch Housing Market [J]. Urban Studies, 2011, 48(5): 997-1015.

[6] 程开明, 李金昌. 城市偏向、城市化与城乡收入差距的作用机制及动态分析[J]. 数量经济技术经济研究, 2007, (7): 116-125.

[7] 胡晓. 收入差距与中国房地产价格:理论与实证——兼论当前房地产调控的有效性[J]. 财经科学, 2010, 12: 83-90.

[8] O'Flaherty B. An economic theory of homelessness and housing [J]. Journal of Housing Economics, 1995, 4(1): 13-49.

[9] Quigley J M, Raphael S, Smolensky E. Homeless in America, homeless in California [J]. The Review of Economics and Statistics, 2001, 83(1): 37-51.

[10] 陈健, 陈杰, 高波. 信贷约束、房价与居民消费率——基于面板门槛模型的研究[J]. 金融研究, 2012, (4): 45-74.

[11] Hansen B E. Threshold effects in non-dynamic panels: Estimation, testing, and inference[J]. Journal of Econometrics, 1999, 93(2): 345-368.

[12] Lee C C, Chiu Y B. The impact of real income on insurance premiums: Evidence from panel data[J]. International Review of Economics and Finance, 2012, 21(1): 246-260.

[13] Fouquau J, Hurlin C, Rabaud I. The Feldstein-Horioka puzzle: A panel smooth transition regression approach[J]. Economic modeling, 2008, 25(2): 284-299.

[14] Duarte R, Pinilla V, Serrano A. Is there an environmental Kuznets curve for water use? A panel smooth transition regression approach[J]. Economic modeling, 2013, 31(3): 518-527.

[15] Jude E C. Financial Development and Growth：A Panel Smooth Regression Approach[J]. Journal of Economic Development, 2010, 35(1): 15-33.

[16] Omay T, znur Kan E. Re-examining the threshold effects in the inflation-growth nexus with cross-sectional dependent non-linear panel: Evidence from six industrialized economics[J]. Economic Modeling, 2010, 27(5): 996-1005.

[17] 骆永民. 城市化对房价的影响: 线性还是非线性?—基于四种面板数据回归模型的实证分析[J]. 财经研究, 2011,37(4): 135-144.

[18] Wang J C, Holan S H. Bayesian multi-regime smooth transition regression with ordered categorical variables[J]. Computational Statistics and Data Analysis, 2012, 56(12): 4165-4179.

[19] Gonzalez A, Teasvirta T, Dijk D. Panel Smooth Transition Regression Models [R]. Working Paper Series in Economics and Finance, 2005, No. 604.

[20] Lopes H F, Salazar E. Bayesian model uncertainty in Smooth Transition Autoregression[J]. Journal of Time series Analysis, 2006, 27(1): 97-117.

[21] 白凡. 对外贸易差额与货币供给——基于国别面板数据的实证研究[J].湖南大学学报(社会科学版), 2013, 27(6)：74-78.

Bayesian inference on Price of the Real Estate ThresholdEffect Based on Panel Smooth Transition Regression Model

ZHU Hui-ming，YOU Wan-hai ，LI Xiao-yi

(College of Business Administration, Hunan University, Changsha 410082, China)

For non-linear relationship between the prevalence of economic variables, resulting in failure of the linear model fitting problems, panel data smooth transition regression models are established .bayesian method is used to address uncertain risk of parameters estimation caused by common estimation algorithm which is difficult to converge. Based on the analysis of model statistic structure and the selection of parameters prior,the Metropolis-Hasting within Gibbs sampling method is utilized to estimate model parameters, predicting parameters in use of Monte Carlo Markov Chain.The empirical research applies Bayesian panel data smooth model to analyze the data in Chinese provinces. The research outcomes indicate that the iteration traces of parameters are convergent, and the Metropolis-Hasting within Gibbs sampling method estimates parameters accurately, resolving the problem difficult to converge, showing the effectiveness of Bayesian panel smooth transition model. Furthermore, the existence of threshold effect in the price of the Real Estate has been certificated.

Price of the Real Estate; Urbanization; Panel Data; Smooth Transition Regression Model; Bayesian Analysis

2014-02-16

国家自然科学基金创新研究群体项目(71221001)；国家自然科学基金项目(71171075，71031004)；教育部博士点基金项目(20110161110025)；湖南省自然科学基金项目(11JJ3090)

朱慧明(1966—)，男，湖南湘潭人，湖南大学工商管理学院教授、博士生导师.研究方向：贝叶斯计量经济模型.

F293.3

A

1008—1763(2014)05—0066—08