含二次隔振架的双机驱动振动机的自同步理论研究

李 鹤， 刘 丹， 姜 来， 赵春雨， 闻邦椿

(东北大学 机械工程与自动化学院， 沈阳 110819)

含二次隔振架的双机驱动振动机的自同步理论研究

李 鹤， 刘 丹， 姜 来， 赵春雨， 闻邦椿

(东北大学 机械工程与自动化学院， 沈阳 110819)

研究了一种含有二次隔振架的双机驱动振动机的运动自同步及其稳定性条件。该振动机由于二次隔振架的作用，既可以保证物料箱具有足够大的振幅便于筛分物料，又能减小振动机传递到地基的动载荷。首先利用拉格朗日方程建立了振动机的运动微分方程，利用平均小参数法得到了偏心转子的无量纲耦合方程；然后由偏心转子耦合方程零解存在条件得到了振动机实现自同步运动条件，并根据Routh-Hurwitz判据得到振动机同步运行的稳定性条件。最后，通过数值仿真验证了理论分析的正确性。

自同步运动；振动机；稳定性；隔振

自同步现象最早是荷兰物理学家Huygnens在1665年发现的。1953年，前苏联Blekhman等最早研究了振动机械中的自同步理论。Blekhman等[1-2]利用两台相互独立的偏心电机驱动振动机工作，发现在一定参数下可以实现两偏心电机同相位、同转速的同步运动。他发现当系统受到外界干扰导致两电机的转速或相位差发生变化时，系统可以通过自我调整而重新回到同步状态；对于已经实现同步运转的系统，如果切断一台偏心电机的电源，两台电机仍然能够同步运行。

在我国，闻邦椿等[3]采用积分平均方法从平均意义上求得了振动机械的自同步条件和自同步稳定性条件。赵春雨等[4-7]利用改进的小参数平均法发展了双电机驱动和四电机驱动振动系统的自同步理论，深入阐述了振动系统的耦合动力学特性和动态对称性。彭琼梅等[8]研究了直线振动筛的自同步机稳定性。侯勇俊[9]研究了双轴二倍频振动筛的自同步及稳定性。

目前，国内外学者已经对多种振动机的自同步理论有了深入的研究，但对于含有隔振架的振动机自同步理论的研究尚不多见。由于机器运转而形成的振动不但影响附近机器设备的正常工作，还会引起机器本身结构和部件的损坏，降低工作效率，并对人体健康造成危害。因此，必须隔离振动机传递到地基的动载荷。本文研究了一种含有二次隔振架的双机驱动振动机的自同步运动条件和自同步运动稳定性条件。首先，利用拉格朗日方程建立了振动系统的运动微分方程，然后推导出系统实现自同步的条件及自同步稳定性条件，并对系统进行数值仿真，验证了理论分析的正确性。

1 振动机运动微分方程

图1为含二次隔振架振动机的动力学模型，由物料箱质体m1、支撑质体m2、隔振质体Mr以及两偏心转子m01和m02组成。物料箱质体m1在x,y方向分别通过软弹簧kx,ky与支撑质体m2相连接，支撑质体m2在z方向通过硬弹簧kz与隔振质体Mr相连接，且在x,y方向被固定，隔振质体Mr支撑在弹性基础kzr上。两偏心转子分别由感应电动机1和2驱动，对称安装在物料箱质体m1质心o所在水平面xoy的两侧，其旋转平面与该水平面成δ角，且两偏心转子旋转中心与物料箱质体质心在同一条竖直轴上。俯视时，两偏心转子同向回转。

图1 含二次隔振架振动机的动力学模型Fig.1 Dynamic model of the vibrating systemwith a two-stage vibration isolation frame

利用拉格朗日方程，可以得到系统的运动微分方程:

(1)

式中，M1为振动系统在x,y方向的振动质量，M1=m1+m01+m02；M2为振动系统在z方向的振动质量，M2=m1+m2+m01+m02；kx,ky,kz,kzr为振动系统在x,y,z,zr方向弹簧刚度，fx,fy,fz,fzr为振动系统在x,y,z,zr方向阻尼系数，fd1,fd2为两电动机的阻尼系数;φ1,φ2为两偏心转子的相位，r为两偏心转子的旋转半径，Te1,Te2为两电动机的电磁转矩。

令m01=m0,m02=ηm01，利用模态叠加法，可以解得式(1)中前四个方程的振动响应：

(2)

其中，

ax=kx-M1ω2,bx=fxω,ay=ky-M1ω2,by=fyω,

a=MrM2ω4-[Mrkz+M2(kz+kzr)+fzfzr]ω2+kzkzr

b=-[Mrfz+M2(fz+fzr)]ω3+(fzkzr+fzrkz)ω

cz=kz+kzr-Mrω2,dz=(fz+fzr)ω,czr=kz,

dzr=fzω,γx=arctan(bx/ax),γy=arctan(by/ay),

2 两偏心转子的同步条件

2.1 两偏心转子的无量纲耦合运动方程

设振动系统稳态运行时两偏心转子的平均相位为φ，且偏心转子1超前偏心转子2的相位为2α，即

2φ=φ1+φ2, 2α=φ1-φ2

(3)

则偏心转子1和2的相位分别为

φ1=φ+α,φ2=φ-α

(4)

(5)

将式(5)代入式(4)，且令v1=ε1+ε2,v2=ε1-ε2可得两偏心转子的角速度和角加速度分别为

(6)

当系统处于稳定运行状态时，将式(4)、(6)代入系统在各方向的振动响应式(2)，并引入以下无量纲参数

ny=ωm0/ωny,nz=ωm0/ωnz,nzr=ωm0/ωnzr

rm=m01/M1,σ=M1/M2,τ=M2/Mr,

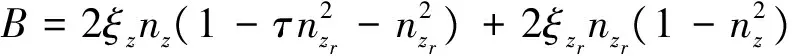
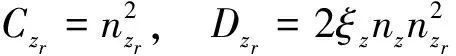
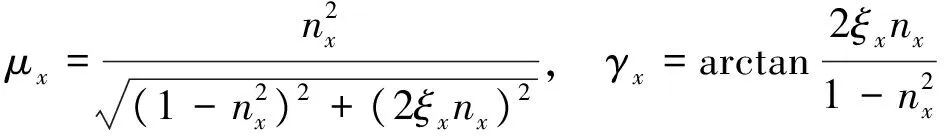
(8)

其中，

(9)

式(9)中各参数为

χ22=η2Ws0

Ws0=rm(μxcos2δsinγx+μysinγy+μzσsin2δsinγz)

Wc0=rm(μxcos2δcosγx+μycosγy+μzσsin2δcosγz)

Wcs=ηrm(μxcos2δsinγx+μysinγy-μzσsin2δsinγz)

Wcc=ηrm(μxcos2δcosγx+μycosγy-μzσsin2δcosγz)

在式(8)中，当两电动机在ωm0附近运行时，其电磁转矩为

(10)

式中Te01,Te02为两电动机以ωm0即稳态运行时的电磁转矩；ke01,ke02为两电动机以ωm0即稳态运行时的刚度系数。

在式(8)中，两电机的转动惯量J01和J02远小于m01r2和m02r2，可以忽略，将式(10)代入式(8)得

(11)

将式(9)代入式(11)，并引入下列无量纲参数

ρ1=1+Wc0/2,ρ2=η+η2Wc0/2

整理式(11)，并写成矩阵形式

(12)

其中，

2.2 系统实现同步条件

(13)

将式(13)中两项相减并整理可得

(14)

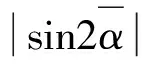
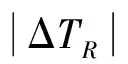
(15)

即振动系统的同步力矩大于或者等于两电机剩余电磁转矩差的绝对值。

(16)

式中,TL为振动系统作用在两电机上的负载力矩。

定义振动系统的同步力矩与作用在两电机上负载力矩的比值的绝对值为振动系统的同步能力系数ζ[7]，即

(17)

同步能力系数ζ表示振动传送力矩克服两电动机电磁转矩实现同步的能力，当其值大于1时表示系统可实现振动同步传动，即一个电动机停止电源供电，系统仍然可保持同步运行[7]。

2.3 系统自同步运动稳定条件

(18)

其中，

C=A′-1B′

a13=0,a23=0,a31=0,a32=0,a33=1

b31=0,b32=-1,b33=0

通过C=A′-1B′求出矩阵C，进而通过det(C-λI)=0得到矩阵C的特征方程如下

λ3+c1λ2+c2λ+c3=0

(19)

其中，

(20)

由Routh-Hurwitz准则可知，当矩阵C的特征方程(19)参数满足

c1>0,c3>0,c1c2>c3

(21)

时，平凡解z=0是稳定的。式(21)可进一步写成:

H0>0,H1>0,H3>0, 4H1H2>H0H3

H0<0,H1<0,H3<0, 4H1H2>H0H3

(22)

由于振动系统的工作频率大于4倍的非共振方向固有频率，阻尼比较小(ξ≤0.07)。则振动系统结构满足H0>0[7]，从而系统同步运行稳定性条件为

H1>0,H3>0,H>0

(23)

其中，H=4H1H2-H0H3。

3 振动机自同步运动数值分析

3.1 隔振参数的选择

通过数值仿真，进一步讨论该振动机的自同步。由于本文所研究的含隔振架的振动系统既要保证有足够大的振幅以达到筛分物料要求，又要实现隔振以减小对基础的动载荷冲击。因此在选择系统参数时，应优先考虑隔振质体(Mr)与振动方向质量(M2)的比值。

首先选取物料箱质体质量m1=2 200 kg，支撑质体质量m2=300 kg，从而系统在z方向的振动质量M2=2 500 kg。而通常情况下，当隔振质量为振动质量的0.5倍，即τ=2.0时，二次隔振效果最好，从而选取隔振质体质量为Mr=1 250 kg。

由式(7)可知，系统在z方向的振幅取决于μz的大小，隔振质体的振幅与系统z方向的振幅的比值为τμzr/μz。当选取τ=2.0时，μz和τμzr/μz的大小与系统参数nz,nzr有关，如图2所示。

图2 μz、τμzr/μz与系统参数nz、nzr的关系Fig. 2 Relation between μz、τμzr/μz and the parameters nz、nzr of the vibrating system

由图2(a)可知，只有当nzr足够小时，系统在z方向才有可能达到共振， 使得物料箱质体有足够大的振

幅；每一个nzr对应一个nz使得系统在z方向达到共振，当选取nzr=0.3时，nz=0.9；nzr越小，所对应的nz越大，但共振振幅略有降低。

由图2(b)可知，当nzr≥1时，隔振质体Mr的振幅将大于系统z方向的振幅，起不到隔振效果，当nzr<1时，nzr越小，隔振效果越好；当选定nzr时，随着nz增大，隔振质体的振幅与系统z方向的振幅的比值τμzr/μz逐渐减小，隔振效果也越好。

由图2可知，应选择较小的nzr和与之相对应的能够使系统在z方向达到共振的较大的nz，从而满足系统既能在z方向有足够大的振幅以达到筛分物料要求，又能实现隔振以减小对基础的动载荷冲击的要求。因此，选取τ=2,nzr=0.3,nz=0.9。

3.2 振动机自同步能力

对系统同步能力系数ζ与振动系统结构参数进行研究，数值计算结果如图3所示。

由图3(a)可知：在η=1.0,σ=0.9,nz=0.9,nzr=0.3确定情况下，系统同步能力系数ζ随着共振激励角δ的增大而迅速减小，当τ=2.0且δ=0.112π时，ζ=0.999即振动系统将不能实现振动同步传动，可见共振激励角δ对系统的同步能力影响较大，从而为了保证振动系统能够在共振状态下仍可实现π相位同步，应合理选取较小的共振激励角δ。

由图3(b)可知：在其他系统结构参数τ=2.0,σ=0.9,nzr=0.3,δ=π/8确定情况下，系统同步能力系数ζ随着两偏心转子质量比η的增大而增大，当η=1.0即振动系统对称时，系统同步能力系数ζ达到最大值，从而在实际机构设计中，应选取两相同偏心转子以提高振动系统的同步能力。

由图3(c)可知：在其他系统结构参数η=1.0,τ=2.0,nzr=0.9,δ=π/8确定情况下，随着振动系统在x,y方向的振动质量与在z方向的振动质量的比值趋近于1(即σ→1.0)，系统同步能力系数ζ略有降低，可见其对振动系统的同步能力影响较小，可以通过增加支撑刚体质量来提高振动系统的同步能力。

(a) η=1．0，σ=0．9，nz=0．9，nzr=0．3(b) τ=2．0，σ=0．9，nzr=0．3，δ=π/8(c) η=1．0，τ=2．0，nz=0．9，δ=π/8图3 同步能力系数ζ与振动机结构参数的关系：Fig．3Relationbetweenthecoefficientofsynchronizationabilityζandthestructuralparametersofthevibratingsystem

综上，系统同步能力系数ζ与系统结构参数η为正相关，与系统结构参数σ以及δ为负相关。由3.1分析可知，为了满足振动系统在z方向达到共振以及实现较好隔振效果的要求，应选取τ=2.0,nzr=0.3,nz=0.9。而由图3可以看出，当τ=2.0,nzr=0.3,nz=0.9时，系统同步能力系数ζ达到最小值。从而在实际机构设计中，应采取选两相同偏心转子、减小共振激励角δ以及增加支撑刚体质量等措施来提高振动系统的同步能力。

3.3 振动机自同步运动

选取物料箱质体的质量m1=2 200 kg，支撑质体的质量m2=300 kg，隔振质体的质量Mr=1 250 kg，两偏心转子的质量m01=40 kg，m02=40 kg。从而可确定隔振振动系统的结构参数：rzr=0.017 5，η=1.0，σ=0.883 7，τ=2.064。选取两电机为鼠笼式三相异步电动机(380 V，50 Hz， 6-pole， Δ连接)，电机1(3.7 kW，980 r/min)，电机2(0.75 kW，980 r/min)。由前述研究可知，当τ=2.064时，选取系统结构参数nz=0.9以及nzr=0.3，既能满足振动方向有足够大的振幅又能实现隔振以减小对基础的动载荷冲击。另外，选取计算参数nx=ny=4.0，ξx=ξy=ξz=ξzr=0.07。选取δ=15°以及偏心距r=0.2 m，并在6 s时撤去电机2的电磁转矩及9 s时对偏心转子2施加10°的相位扰动，仿真结果如图4所示。

图4 振动机自同步运动数值仿真结果Fig.4 Results of numerical simulation for the self-synchronous motion of the vibrating system

由图4可知：振动机经过4 s左右，两电机转速相同，约为993.1 r/min，此时两偏心转子的相位差稳定在181.4°，系统在各方向的振动也趋于稳定。此时，隔振振动系统实现π相位同步，在z方向做直线运动，振幅达到1.19 mm，能够满足筛分物料的要求。另外，隔振刚体的振动也达到稳定状态，其振幅为0.04 mm，约为振动系统在z方向振幅的1/30，达到比较好的隔振效果。当6 s撤去电机2的电磁转矩时，两电机的同步转速下降并稳定在992.1 r/min，两偏心转子相位差增加并稳定在181.9°左右，但系统在各方向振动仍然处于原稳定状态；当9 s对偏心转子2施加10°的相位扰动时，两偏心转子相位差变为191.9°，两电机转速及系统在各方向振动也发生波动，但经过约1.5 s后均恢复到受干扰前的稳定状态。从而，通过计算机仿真可证明隔振振动系统能够实现π相位同步稳定运行、同步振动传动以及对相位扰动的抗干扰能力，同时满足系统在振动方向达到较大振幅以及实现较好隔振效果的要求。

4 结 论

本文研究了一种含有二次隔振架的双机驱动振动机的运动自同步条件及其稳定性条件。利用拉格朗日方程建立了系统运动微分方程；利用模态叠加法求得系统耦合运动微分方程的振动响应；借助平均小参数法得到了两偏心转子的无量纲耦合方程；推导出了系统实现自同步运动条件及自同步运动稳定条件；通过数值仿真验证了理论的正确性。得到如下结论：

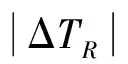
(2) 利用Routh-Hurwitz准则，得到系统自同步运动稳定条件为：H1>0,H3>0,H>0，其中，H=4H1H2-H0H3。

(3) 系统在z方向的振幅取决于μz，隔振质体的振幅与系统z方向的振幅的比值为τμzr/μz。而μz和τμzr/μz取决于隔振质量比τ、振动方向频率比nz以及隔振方向频率比nzr，为了取得较好的隔振效果，选取τ=2,nzr=0.3,nz=0.9。此时，振动机即可以保证物料箱质体在z方向具有足够大的振幅以达到筛分物料要求，又具有较好隔振性能以减小对基础的动载荷冲击。但此时系统自同步能力最小，可以通过采取选两相同偏心转子、减小共振激励角δ以及增加支撑刚体质量等措施来提高振动系统的同步能力。

(4) 数值仿真结果验证了理论分析的正确性，当振动机的参数满足系统自同步运动条件和自同步运动稳定条件时，振动机能够很快实现自同步运动并达到稳定的自同步运动状态，且振动机具有较好的隔振性能。

[1] Blekhman I I, Fradkov A L, Tomchina O P, et al. Self-synchronization and controlled synchronization: general definition and example design [J]. Mathematics and Computers in Simulation, 2002, 58: 367-384.

[2] Blekhman I I. Selected topics in vibrational mechanics [M], Singapore: World Scientific, 2004.

[3] 闻邦椿，李以农，张义民，等. 振动利用工程[M].北京：科学出版社，2005.

[4] ZHAO Chun-yu, ZHANG Yi-min, WEN Bang-chun. Synchronization and general dynamic symmetry of a vibrating system with two exciters rotating in opposite directions[J]. Chinese Physics B, 2010, 19(3): 030301.

[5] ZHAO Chun-yu, WEN Bang-chun，ZHANG Xue-liang. Synchronization of the four identical unbalanced rotors in a vibrating system of plane motion [J], Science China, 2010, 53(2): 405-422.

[6] ZHAO Chun-yu, ZHU Hong-tao, BAI Tian-ju, et al. Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linear motion. Part II: numeric analysis[J]. Shock and Vibration, 2009, 16(5): 517-528.

[7] ZHAO Chun-yu, ZHU Hong-tao, ZHANG Yi-min, et al. Synchronization of two coupled exciters in a vibrating system of spatial motion[J], Acta Mechanica Sinica, 2010, 26(3): 477-493.

[8] 彭琼梅,尹友中.自同步直线振动筛的动力学分析及实际应用[J].建设机械技术与管理,2005,18(9):84-87. PENG Qiong-mei,YIN You-zhong.Dynamic analysis of autosynchronous linear vibrating sieve and its practical application[J]. Construction Machinery Technology & Management,2005,18(9):84-87.

[9] 侯俊勇.双轴二倍频振动筛的自同步及稳定性[J].西南交通大学学报,2012,47(1):104-108. HOU Jun-yong. Self-synchronization and stability of two-times frequency shaker excited by bi-shaft[J]. Journal of Southwest Jiaotong University, 2012, 47(1): 104-108.

Self-synchronization theory of a vibrating system with a two-stage vibration isolation frame driven by two motors

LI He， LIU Dan， JIANG Lai， ZHAO Chun-yu， WEN Bang-chun

(School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China)

The conditions of self-synchronization and motion stability regarding a dual-motor-drive vibrating system with a two-stage vibration isolation frame were studied. Owing to the effect of the two-stage vibration isolation, this system had not only enough oscillation amplitude of its material box to screen a material, but also reduced the dynamic load transmitted to the foundation. Here, firstly utilizing Lagrange equation, the differential motion equations of the vibrating system was built. Then, with a modified average small parameter method, the dimensionless coupled equations of eccentric rotors were derived. Furthermore, the condition of existence for zero solution to the dimensionless coupled equations of the eccentric rotors was used to achieve the condition to implement the self-synchronous motion of the vibrating system, and the stability condition of self-synchronous motion was obtained with Routh-Hurwitz criterion. Finally, the numerical simulations were performed to verify the correctness of the theoretical analysis.

self-synchronous motion; vibrating system; stability; vibration isolation

国家自然科学基金(51175071)；中央高校基本科研业务费专项基金资助项目(N120203001)

2013-04-24 修改稿收到日期：2013-06-04

李鹤 男，博士，教授，1975年10月生

TH113

A

10.13465/j.cnki.jvs.2014.08.024