采用多目标进化模型的无监督故障特征选择算法
2014-08-11于德弘
夏 虎 , 庄 健 , 周 璠 , 于德弘
(1. 西安交通大学 机械工程学院, 西安 710049;2. 一汽-大众汽车有限公司, 长春 130011)
采用多目标进化模型的无监督故障特征选择算法
夏 虎1, 庄 健1, 周 璠2, 于德弘1
(1. 西安交通大学 机械工程学院, 西安 710049;2. 一汽-大众汽车有限公司, 长春 130011)
高维故障特征数据易影响诊断的处理速度和识别率,而传统单目标特征选择算法易融入主观偏好,从而影响特征选择的质量。为此,提出一种无监督的多目标进化特征选择算法。采用熵度量作为相关度目标,采用相关系数的概念设计了冗余度目标,算法同时将这两个目标作为优化对象;利用样本在各个特征上的分布信息,设计了导向性的种群初始化过程和变异算子,以提高算法的优化能力;还利用集成的方法得到了所有特征的重要度序列。对5组UCI数据和3组往复式压缩机故障数据的测试结果表明,该算法比已有的几种特征选择算法更具优势。
特征选择;多目标进化算法;冗余度;故障诊断
随着机械设备的复杂化和大型化,从信号中提取单一特征用以监测设备运行状态的方法往往难以满足实际需求。而另一方面,多种信号的获取途径(如利用不同类型的传感器或不同的测试位置)和丰富的信号处理技术则为研究人员提供了大量的特征。因此,基于多种特征的故障诊断技术被许多研究人员采纳[1-3],成为一种发展趋势。然而这些特征数据包含不少无关和冗余的信息,如果直接应用于故障诊断,不仅增加了问题求解的复杂度,还可能影响诊断的准确度。所以,设计合理的特征选择算法用以提取合适的特征子集成为必要。
特征选择本质上是一个组合优化问题。当特征维数过高时,穷举的方法难以在多项式时间内找到最优解。因此,许多学者利用贪婪搜索或智能优化的方法搜索最优解,取得了很好的效果;文献[4]提出一种基于熵度量的序列后向选择算法;文献[5]提出一种基于进化蒙特卡洛方法的特征选择算法并用于滚动轴承的故障诊断;文献[6]则采用粒子群优化技术提取齿轮传动箱的故障特征;但是,上述优化算法通常以某一个评价指标作为优化对象,只能从单个角度评价求解质量,影响了特征选择的效果。比如,文献[4]采用的熵度量方法主要反映了特征与数据结构间的相关度,而没有考虑已选特征之间的冗余度,造成获取的特征子集可能保留了一些冗余特征,而忽视了一些重要的特征。
多目标进化优化技术可以从多个角度评价特征子集的质量,并将这些评价指标作为目标函数同时进行优化,避免了单一目标引起的偏好。目前已有学者提出了各自的多目标特征选择算法[7-8],它们都是在已有单目标优化技术的基础上,将最小化特征子集的规模作为另一个优化目标;但是特征子集的规模是一个离散目标,通常求得的解集中每个特征规模下只能对应一个解,这使得规模相同但具体特征不同的其它特征子集无法被发现。而这些特征子集对于故障诊断也是有用的。举例说明:假设特征子集1包含a、b两个特征,特征子集2包含a、c两个特征,二者的性能相近;但b和c来自于不同的信号源,若只得到特征子集1,当b所需的信号无法提供时(如传感器不便于安装),所得的解将丧失意义。此外,多目标特征选择算法最终得到的是一系列的折中解,需要从中选取性能优良的解,但目前可用的无监督方法还较少[7]。
针对上述问题,本文在已有研究基础上,提出一种新的多目标进化特征选择算法(Multi-Objective Feature Selection Algorithm,MOFS)。该算法具有以下特点:① 从相关度和冗余度两个角度评价特征子集的质量,能够获取多个特征规模相同的特征子集,为诊断人员提供了更多的决策空间;② 利用样本间的距离值构建相关度和冗余度这两个目标函数,使得本文算法为一种无监督的方法,利于在样本类标记信息缺乏或者不完全的情况下完成故障特征的选取;③ 设计一种集成方法将所得各个特征子集进行融合,得到特征的重要度序列,从而自动产生一个最优的解。最后,通过对多组UCI数据,往复式压缩机气阀泄漏故障和气缸划伤故障数据的测试,表明本文算法性能优于多种已有的特征选择算法。
1 目标函数设计
利用相关度和冗余度的概念定义了一组最小化的目标函数,用以评价特征子集的质量。其中相关度倾向保留所有与数据结构关联紧密的特征,而冗余度则会排除与已选特征相关度高的特征,二者存在一定的矛盾关系,是典型的多目标优化问题。
相关度目标采用文献[4]所提的熵度量指标,其定义为
(1)
Sij=exp(-αDij)
(2)
其中,N是数据样本的个数;α是一个权重系数,由式(2)计算所得;Dij是样本i和样本j在x所表示的特征子集下的欧式距离;Da表示所有样本在全空间下欧式距离的平均值。在计算目标值之前,Sij的取值必须归一化到[0,1]。当选择的特征子集合理时,样本i和样本j若属于同类,则Sij的取值很小,若属于异类,则Sij的取值很大。根据函数SijlgSij+(1-Sij)lg(1-Sij)的特性,Sij取值接近0或者1时,该函数的取值均会很小,从而使得好的特征子集对应较小的f1(x)取值。
冗余度目标则利用了相关系数的概念,当相关系数的绝对值越小,特征子集所包含的冗余就越小。该目标具体设计为
(3)
其中,nx表示特征子集的个数;d是总的特征个数;xj和xk分别表示x中第j个和第k个元素的取值;bij表示第i个样本在第j个特征上的取值,baj表示所有样本在第j个特征上的均值。当被选中的两个特征越相关,则|cjk|的取值越接近1,而当两个特征越独立,则取值越接近0。因此在特征子集规模确定的情况下,冗余度小的特征子集对应的目标函数f2(x)的取值会更小。
2 多目标特征选择算法的设计
本文提出的多目标特征选择算法采用二元编码方式,个体x={x1,x2,…,xd},x的取值范围为{0,1}d,当取值为1时表示该特征被选中。在初始化阶段,种群中一半数量的个体采用随机的方式生成,由于合适的特征子集一般远小于总的特征集,因此以较小概率p1决定某一个特征被选中;另一半数量的个体则利用特征的分布信息生成。具体而言,计算所有样本取值在各个特征上的方差,然后根据式(4)计算特征被选中的概率p2。式(4)的表达式为
(4)
其中vj表示在第j个特征上所有样本取值的方差。方差越大,样本的分布就越分散,表明不同类的数据在该特征上越易被区分。而在公式(4)中,当第j个特征方差取值较大时,它的比值容易超过平均水平,使得概率p2大于0.5,从而该特征更易被选中。
为了便于下文的理解,这里给出多目标优化的一些相关概念。若个体x1和x2满足fi(x1)≤fi(x2),i=1,2,…,m,m为目标函数的个数,并且至少在一个目标函数上满足fi(x1) 2.1 交叉、变异算子设计 交叉所需的父代个体采用二元联赛选择的方法获取,即:① 随机选取个体x1和x2,比较二者的Pareto支配关系,选取Pareto占优解作为父代个体;② 若二者互不支配,则比较它们在目标空间的邻域密度,密度小的个体选为父代个体,其中密度评估方法采用经典的拥挤距离方法[9];③ 若二者密度相同,则等概率随机选取。算法中的交叉算子采用双点交叉的方法,即随机选取两个交叉点u和v,父代个体{x11,…,x1u,…,x1v,…,x1d}和{x21,…,x2u,…,x2v,…,x2d}交叉后为{x11,…,x2u,…,x2v,…,x1d}和{x21,…,x1u,…,x1v,…,x2d}。 本文设计了一种抗冗余度的变异算子。首先以概率p3决定当前个体是否进行变异,若被选中,则随机选取其中一维jr,根据式(3)计算第jr个特征与其他已经被选中特征之间的相关系数。然后从中选取相关系数绝对值的最大值,记为p4。若xjr=1,则以概率p4令xjr=0;若xjr=0,则以概率1-p4令xjr=1。该变异的含义为:当第jr个特征已经被选中时,若p4取值很大,说明它与某个被选中的特征冗余,则以较大概率舍弃;当第jr个特征未被选中时,若p4取值很小,说明它与被选中的特征之间冗余度小,则以较大概率1-p4选入特征子集。 2.2 算法流程 决策者从Pareto解集中选取一个特征子集时需要对多个解进行测试,增加了工作量,并且决策者有时还需要得到特征的重要度序列。为此本文设计了一种集成方法对特征进行排序,决策者只需要指定特征个数即可获得相应的特征子集。其具体方法为:① 计算每个Pareto解对应的特征子集的规模,将所有规模为z的解存入同一个集合中,记为Sz,z∈[1,d];② 对每个集合,选择函数值f1最小的解,放入集合A,选择函数值f2最小的解,放入集合B;③ 分别计算集合A和B中每个特征被选中的次数,记为tAj和tBj;④ 按照式(5)计算第j个特征的重要度wj,取值越大表明越重要。 wj=tAj+rtBj (5) 其中r表示权重系数,因为目标函数f2不能单独用于提取重要特征,集合B施加的影响应弱于集合A,所以r取值在(0,1)之间。 将所有特征的重要度值降序排列即为最终的集成结果。若指定特征子集规模z,则前z个特征即为最优特征子集。 4.1 UCI数据测试 5组UCI数据分别为Iris、Monk3、Wine、Australian和Glass。将各个算法所得结果按重要度降序排列,结果如表1所示。MOFS1的特征重要度排序方法为:统计每个特征在所得Pareto解集中出现的次数,次数越多越重要。由于Iris和Monk3的重要特征是已知的,可用以检验算法是否能正确选取特征,其中重要特征对应的序号用黑色加粗字体表示。Iris和Monk3的测试结果表明所有算法均能正确选出重要的特征。进一步的,本文采用C50算法测试各个算法在Wine、Australian和Glass数据集上的分类正确率,结果如图1所示。可见,三种算法在Wine和Glass数据集上有相似的性能;但是在Australian数据集上,MOFS性能要优于其它两种方法,其在较小特征子集规模下已达到较高正确率,说明所得的特征重要度序列更加合理。 4.2 压缩机故障数据测试 压缩机故障数据由图2所示实验平台获得。该平台通过加速度传感器获取缸盖上方的振动信号,通过压力和温度传感器获取各级阀腔进气口和出气口的压力、温度信号,以及储气罐出口处的压力信号。加速度传感器频率测量范围为0.7~10 kHz,采集频率为40 kHz,温度和压力信号的采集频率为1 kHz。以主轴旋转10圈(约0.6 s)时间所采集的信号作为一个样本来源,提取不同传感器所得信号的特征。按照文献[3]所列常见特征,加速度信号提取的特征包括原始信号的11个时域特征,13个高频(3 ~10 kHz)频域特征和13个低频(0.7~3 kHz)频域特征,以及3层db10小波重构后的高频和低频特征。阀腔压力信号的特征包括平均压力,最大压力和最小压力。阀腔温度信号的特征包括平均温度和温度变化率。储气罐出口压力信号的特征包括平均压力和压力变化率。数据集VData1为一级缸气阀泄漏故障数据,包含50个正常工况的样本,50个进气阀2 mm通孔泄漏的样本,50个排气阀2 mm通孔泄漏的样本和50个进排气阀均2 mm通孔泄漏的样本。数据集VData2为二级缸进气阀泄漏故障数据,包含50个正常样本,以及进气阀1 mm、2 mm、 3 mm和5 mm通孔泄漏的样本各50个。数据集CData1为二级缸气缸内壁划伤故障数据,包含50个正常样本,50个进气阀2 mm通孔泄漏的样本,50个轻微划伤(一道深1 mm宽2 mm的通槽)的样本,50个严重划伤(两道深1 mm宽2 mm的通槽)的样本,50个轻微划伤并伴随进气阀2 mm通孔泄漏的样本和50个严重划伤并伴随进气阀2 mm通孔泄漏的样本。 表1 不同算法对5组UCI数据所得的特征重要度序列 图1 C50算法在不同特征选择算法所得特征子集上的分类正确率Fig.1 Classification of C50 with different feature subsets 为了保证故障数据处理的快速性和准确性,选取特征子集的规模为7。然后分别将决策树分类算法C50和聚类算法k-means应用于三种特征选择算法所得的特征子集,以检验它们对故障数据特征的选择能力,其结果如表2和表3所示。结果表明:① MOFS对各种故障数据集的分类正确率和聚类质量(RI取值越高越好)均优于另外两种特征选择方法;② MOFS在特征子集上的聚类结果优于在全体特征集上的聚类结果,而EUFS和MOFS1由于特征子集选择的不合适,反而使得在VData2数据集上的聚类质量下降;③ 由于加速度传感器距离气缸划伤的故障源较远,且CData1中包含复合故障,使得故障模式不易区分,所以分类和聚类结果均差于VData1和VData2,但利用MOFS所选特征子集得到的结果仍然具有较高的质量。 表2 不同特征选择算法对压缩机 故障数据分类正确率的影响 A:两级往复式压缩机;B:信号调理模块;C:信号采集模块;D:负载模块(气动马达和磁粉制动器构成)图2 往复式压缩机故障实验平台Fig.2 Experimental platform on fault simulation of reciprocating compressor 数据集MOFSMOFS1EUFS全部特征VData10.98530.95580.94770.9330VData20.94370.88920.90620.9277CData10.93000.87530.88670.8685 提取三种特征选择算法在VData2数据集上所得的前3个重要特征构成一个三维空间,观察样本的分布情况,如图3所示。可见只有MOFS能完全将各个类的样本分离开,而EUFS和MOFS1均有不同类的样本发生重叠。这进一步说明本文算法所得的特征重要度序列能更好的反映特征的真实重要度。 图3 VData2数据集在前三个特征所构成空间下的分布情况Fig.3 Distribution of VData2 in the first tree features obtained by different algorithms 已有多目标特征选择算法以特征数量作为第二个目标函数,使得每个特征子集规模下至多存在一个Pareto解。但是有的特征可能在现场难以获取(如传感器不易安装,特征提取手段复杂等),不利于决策人员的后续操作。而MOFS则可以提供更多的选择空间。以VData2为例,当选定3个特征时,MOFS1只能得到一个解,所选特征均为加速度传感器的频域特征,聚类所得RI指标为0.896 2;而MOFS获得两个解,其中一个解的特征为频域特征,聚类所得RI指标为0.899 2,另一个解的特征为阀腔进气口压力特征,聚类所得RI指标为0. 857 9。虽然后者的聚类质量略差,但许多压缩机提供有压力测点,压力信号更易于获取。 提出的特征选择算法采用了多目标进化模型来实现特征子集的优化。在目标函数方面,设计了相关度和冗余度两个目标函数,既保留了相关特征,又剔除了冗余特征,有效避免了单一目标偏好对特征选择结果的影响。在算子设计方面,利用样本在各个特征上的方差,设计了导向性的初始化方法和变异算子,充分利用了样本中包含的已知信息。在实验方面,该算法在标准UCI数据集和多种往复压缩机复杂故障数据上均取得了很好的效果,能够准确捕捉到重要特征。尤其在故障数据集的识别中,其获得的特征子集在分类正确率和聚类质量上均优于单目标特征选择算法EUFS和仅优化特征数量的多目标特征选择算法MOFS1,以及采用全部特征所得的结果。此外,该算法可以得到多个性能相近的候选特征子集,为决策人员提供了更大的选择空间。 [ 1 ] Niu G,Han T,Yang B S,et al. Multi-agent decision fusion for motor fault diagnosis [J]. Mechanical Systems and Signal Processing, 2007, 21(3): 1285-1299. [ 2 ] Lei Y G,He Z J,Zi Y Y,et al. New clustering algorithm-based fault diagnosis using compensation distance evaluation technique [J]. Mechanical Systems and Signal Processing, 2008, 22(2): 419-435. [ 3 ] Lei Y G,He Z J,Zi Y Y,et al. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs [J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2280-2294. [ 4 ] Dash M,Liu H,Yao L. Dimensionality reduction of unsupervised data [C] // Proceeding of 9th IEEE International Conference on Tools with Artificial Intelligence. IEEE COMP SOC, 1997. 532-539. [ 5 ] 刘晓平, 郑海起, 祝天宇. 基于进化蒙特卡洛方法的特征选择在机械故障诊断中的应用 [J]. 振动与冲击, 2011, 30(10):98-101. LIU Xiao-ping, ZHENG Hai-qi, ZHU Tian-yu. Feature selection in machine fault diagnosis based on evolutionary Monte Carlo method [J]. Journal of Vibration and Shock, 2011, 30(10):98-101. [ 6 ] 潘宏侠, 黄晋英, 毛鸿伟, 等. 基于粒子群优化的故障特征提取技术研究 [J]. 振动与冲击, 2008, 27(10):144-147. PAN Hong-xia, HUANG Jin-ying, MAO Hong-wei, et al. Fault-characteristic extracting technology based on particle swarm optimization [J]. Journal of Vibration and Shock, 2008, 27(10):144-147. [ 7 ] Handl J, Knowles J. Feature subset selection in unsupervised learning via multiobjective optimization [J]. International Journal of Computational Intelligence Research, 2006, 2(3):217-238. [ 8 ] Mierswa I, Wurst M. Information preserving multi-objective feature selection for unsupervised learning [C]// Keijzer M. Proceeding of 8th Annual Genetic and Evolutionary Computation Conference. USA:Assoc Computing Machinery, 2006, 1545-1552. [ 9 ] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.[10] Quinlan R. Data mining tools see5 and c5.0[EB/OL]. http://www.rulequest.com/see5-info.html, 2004. Unsupervised feature selection algorithm with a multi-objective evolutionary model for fault diagnosis XIA Hu1, ZHUANG Jian1, ZHOU Fan2,YU De-hong1 (1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049,China;2. FAW-Volkswagen Automotive Company Ltd, Changchun 130011, China) Feature selection is necessary for high-dimensional fault features since it can improve efficiency and accuracy of a fault diagnosis. However, traditional feature selection algorithm always has a strong bias towards a single criterion, it is harmful to the quality of feature selection. An unsupervised feature selection algorithm based on a multi-objective evolutionary model was proposed to solve this problem. A relevance objective based on entropy measure and a redundancy objective based on correlation coefficients were simultaneously optimized. Both initialization process and mutation operator were also designed by utilizing the distribution information of samples in each feature. Besides, an ensemble method was proposed to obtain the importance sequences. Experiments for five sets of UCI data and three groups of valve fault data of reciprocating compressors demonstrated the better performance of the proposed algorithm. feature selection; multi-objective evolutionary algorithm; redundancy measure; fault diagnosis 国家自然科学基金面上项目(51375363);广东省战略性新兴产业核心技术攻关项目(2012A090100010);西安市科技计划项目(CX1250④) 2013-03-05 修改稿收到日期:2013-06-04 夏虎 男,博士生,1986年6月生 庄健 男,副教授,硕士生导师,1974年6月生 TP391.41 A 10.13465/j.cnki.jvs.2014.08.011
3 基于集成的最优解选取方法
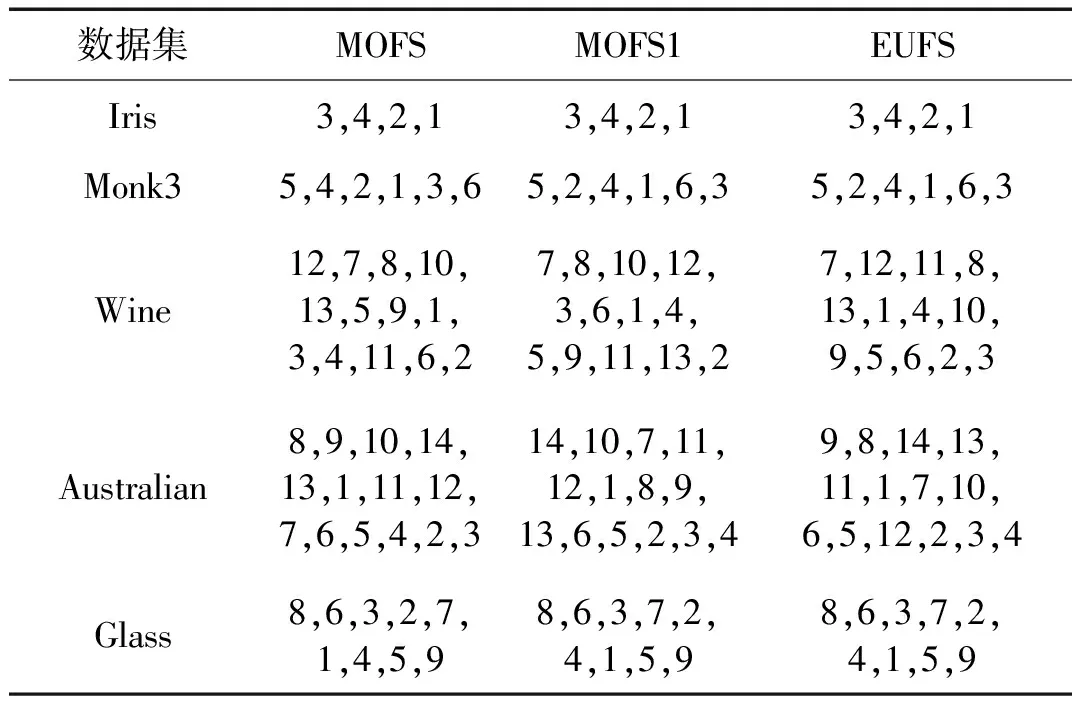
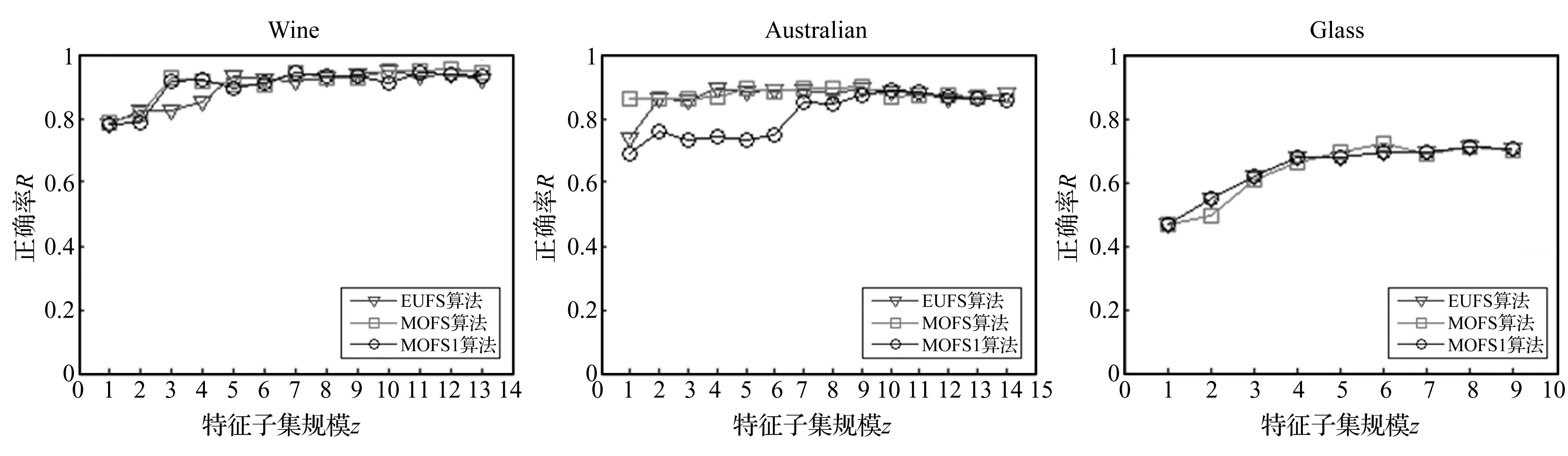
4 实验分析
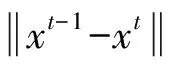




5 结 论
