微元法的应用及其教学启示

陈 平

(江苏第二师范学院数学与信息技术学院，江苏南京 210013)

微元法的应用及其教学启示

陈 平

(江苏第二师范学院数学与信息技术学院，江苏南京 210013)

微元法应用是高等数学教学中的重点部分.本文将结合具体的应用，说明微元法的原理和取法及其产生的教学启示.

定积分；数学教学；应用

积分理论是高等数学教学中的重要部分，而借助积分理论解决实际问题的思想方法即为微元法.因此，微元法成为积分理论应用部分的教学重点，理解微元法是学生学习的难点.本文将结合几何、物理以及经济中的实际问题，引发对微元法的原理及取法的思考并探究其产生的教学启示.

1 微元法的本质与例解

下面，我们将结合几个具体的几何问题来说明微元的选取准则与技巧.

1.1 弧长微元

从而，弧长微元为

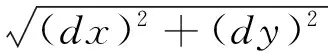
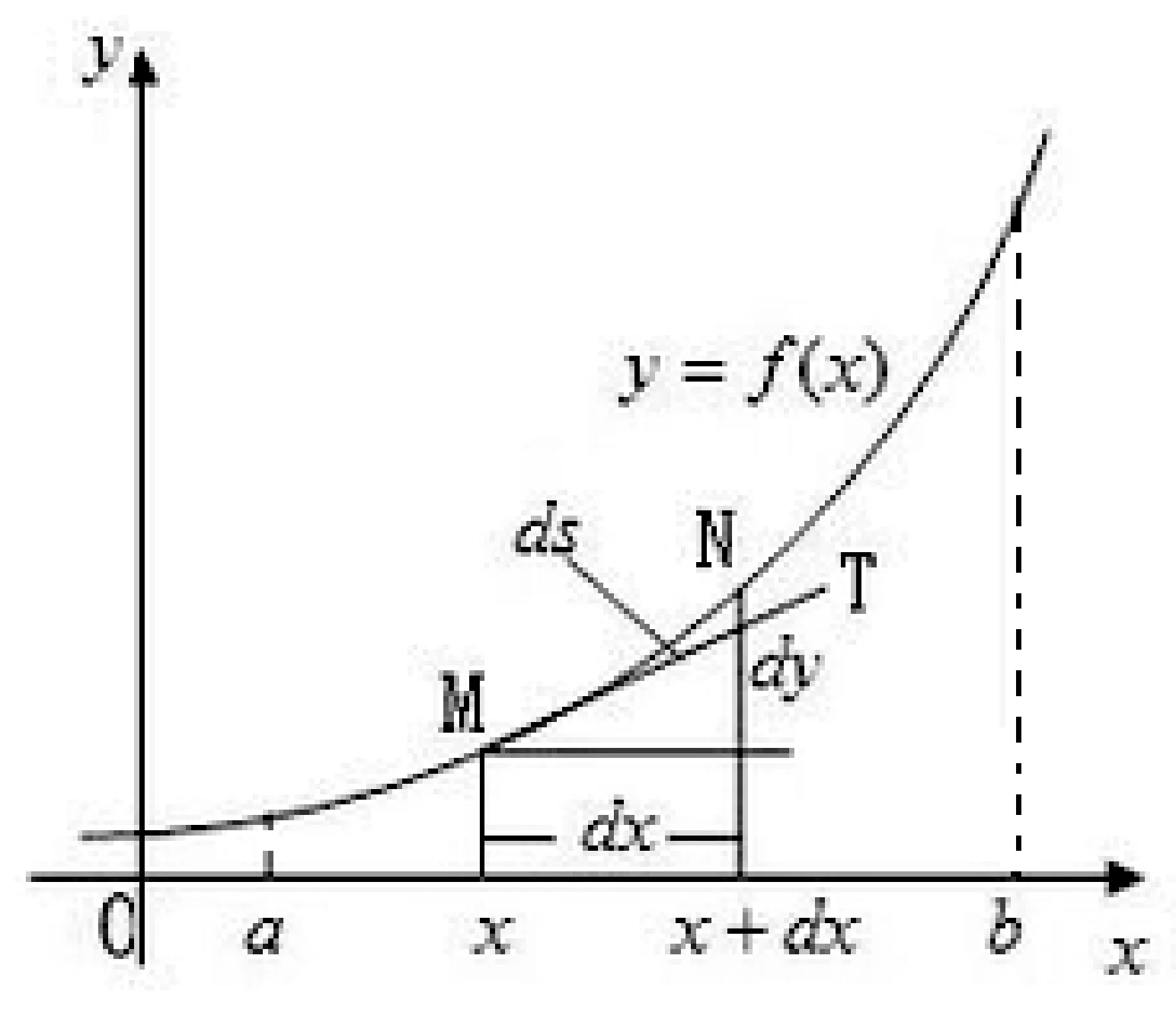
图1 弧长微元

1.2 平面面积微元

求曲线y=f(x)，y=g(x)以及直线x=a，x=b所围成的平面图形的面积微元ds(如图2)，其中对任意x∈[a,b]，有f(x)g(x).利用微元法，在区间[a,b]上任取一小区间[x,x+dx]，并考虑它上面的图形的面积，这块面积可用f(x)-g(x)为高，以dx为底的矩形面积近似，于是ds=[f(x)-g(x)]dx.

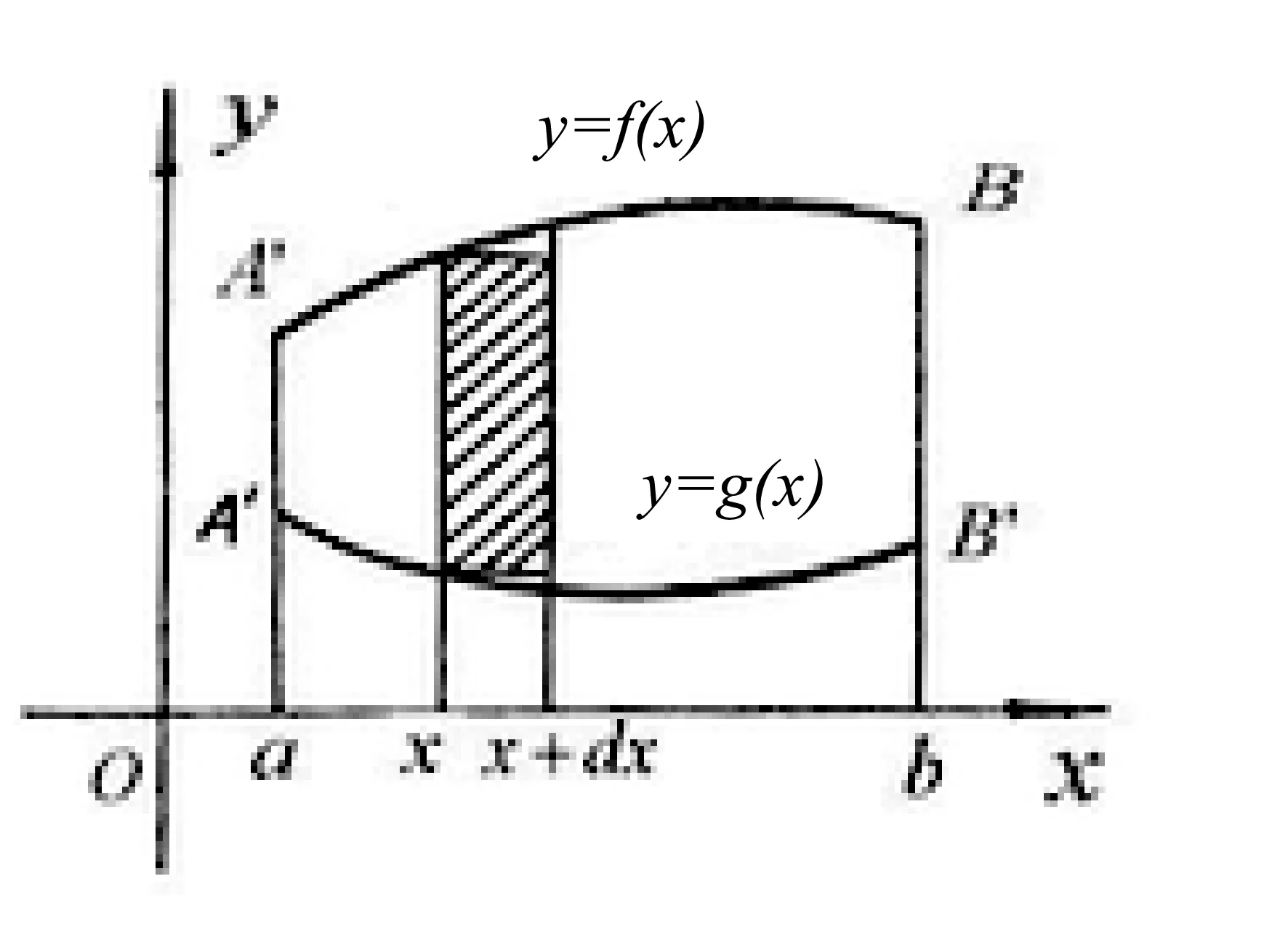
图2 平面面积微元

1.3 已知平行截面面积的几何体的体积微元

现在看图3中的一个空间立体，假设我们知道它在x处截面面积为S(x)，如果像切红薯片一样，把它切成薄片，则每个薄片可近似看作直柱体，其体积等于底面积乘以高.用微元法导出体积微元： 在[a,b]上任取一小区间[x,x+dx]，这样就得到一个非常薄的薄片，并考虑其近似体积(柱体)，于是体积微元为：dV=S(x)dx.

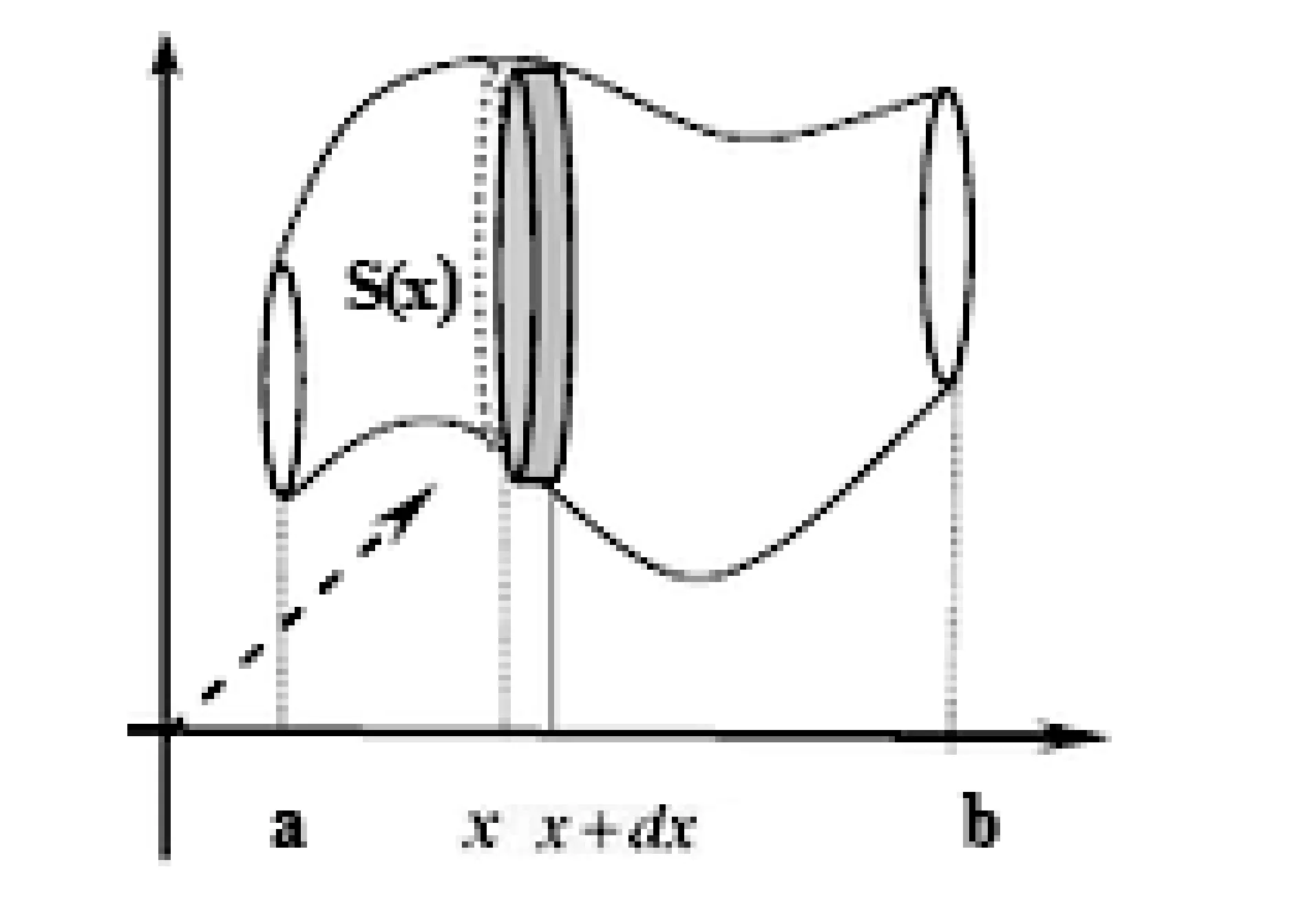
图3 已知截面面积的几何体的体积微元

1.4 旋转体的体积微元

设一平面图形以x=a,x=b,y=0以及y=f(x)为边界，求该图形绕x轴旋转一周的旋转体体积(如图4).我们用“微元法”的思想，来解决这一问题.在[a,b]上任取一小区间[x,x+dx]，得到一个细长条，该细长条我们可以把它看成矩形，该矩形的宽为dx，高为f(x)，那么这个小矩形绕x轴旋转一周的旋转体就是一个非常薄的圆柱体，其厚度就是dx，再由圆柱体体积计算公式，于是小圆柱体的体积微元是：dV=πf2(x)dx.

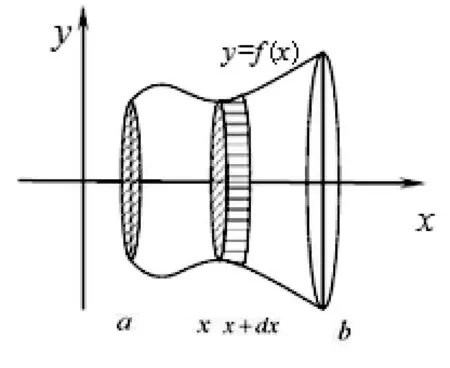
图4 旋转体的体积

1.5 旋转体的侧面积微元

设函数y=f(x)在[a,b]上连续，求其绕x轴旋转所得的旋转体的侧面积.

2 微元法在物理学中的应用

微元法除了可以应用于上述具有几何直观的问题外，还可以解决一些经典的物理问题.

2.1 变速直线运动的路程

已知变速直线运动的质点的运行速度为v=v(t)，求质点在时间段T0到T1内的运动路程.

利用微元法，任取一个时间值t，再给一个时间增量Δt，在这个非常短暂的时间内质点作匀速直线运动，质点的速度为v(t)，其运行的路程为ds=v(t)Δt=v(t)dt，该量即为“路程微元”.

2.2 物质曲线的质量

已知物质曲线的曲线方程为y=f(x),x∈[a,b]，且该曲线在任一点(x,f(x))的线密度为ρ(x)，求该物质曲线的质量.

利用微元法.在曲线上任取一点(x,f(x))，在此点任意截取一小弧段ΔS，该弧段非常微小，小到这段物质弧可以近似看成是均匀分布的，于是该小弧段的质量为

dm=ρ(x)Δs=ρ(x)ds.

由之前的讨论，弧长微元是

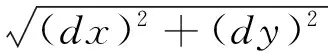
于是，所求物质曲线的质量是

2.3 变力做功问题

设一物体在外力F的作用下，沿力的方向由点a移到点b，已知物体处于点x∈[a,b]时外力F的大小为F(x)，求外力F对物体所做的功.

在点a到点b之间的任意处取定一值x∈[a,b]，并且任给自变量一个增量Δx，由于位移Δx非常小，因此，在这一移动过程中，可以认为作用在物体上的力是恒力，于是得到功微元为

dW=F(x)Δx=F(x)dx.

3 微元法的取元原则与换元技巧

通过上述的实例，可以归纳总结出选取微元时所遵从的基本原则.

3.1 可加性原则

由于微元法的本质是先“化整为零”然后“合零为整”，所以，对“微元”及相应的量的最基本的要求是：应该具备“可加性”原则.具体的，即当区间[a,b]被分割成小区间后，这些小区间通过集合的并运算仍可以整合成区间[a,b]，而对应的“微元”也可以进行“叠加”运算.

3.2 有序性原则

在保证上述可加性原则的基础上，还需保证所选取的“微元”在叠加区域内能够较为方便地获得完整叠加，即做到“不遗漏”、“不重复”.因此在选取“微元”时，需按照关于所求量的某种“序”来选取相应的“微元”.

3.3 可积性原则

除满足上述特征之外，还应要求“微元”可以表达成或者近似表达成某函数(被积函数)与积分变量的乘积，并且这一被积函数在积分变量的变化区间(积分区间)上是可积的.

就“微元法”的应用技巧而言，最为关键的是掌握好换“元”的技巧[2].因为通常的解题中直接选取的“微元”并不一定能使“被积函数”满足可积、容易求积分的性质，这将会给接下来的定积分运算带来困难，所以，必须应用换元的技巧来改变被积函数，来达到简化积分的目的.最常用的换元技巧有如下几种：

(1)“时间元”与“空间元”间的相互代换(表现时、空关系的运动问题中最为常见)，比如求曲线弧长可以利用参数方程形式；

(2)降维法：常见的体积元、面积元与线元间的相互代换；

(3)极坐标变换：常见的极坐标公式是连接“线元”与“角元”间的相互代换的桥梁；

(4)充分利用所求量的各种“对称”特征进行换元.比如图形的奇偶性、区间的对称性、图像的对称轴等等.

4 微元法的教学启示

微元法是高等数学中一个非常重要的思想方法和理论工具[3].它体现了以局部看整体，以微观表宏观，用近似值描述精确值的数学思想，展现了化整为零、积零为整的数学方法.充分体现了极限思想的实质，进而展示了数学上曲直、变与不变、有限与无限这三对矛盾统一体.

在实际教学中，可以将现代教育技术与传统教学模式相结合，探讨微元法思想的教学新模式，引导学生掌握新的思维方式与方法.具体地，可以从如下几个方面着手.

4.1 创设情境

应借助多媒体手段，创设问题情境，即呈现学生熟悉以及感兴趣的问题，激发学生的好奇心、发现欲、诱发质疑猜想从而使其分析和解决问题.

4.2 引入效果评价机制与小组交互型学习模式

教师通过观察记录学生在学习过程中的表现，并结合学生的研究报告，就可以对学生的学习进度进行监控.在小组独立探索问题遇到困难时，教师需要适当给予提示，引发学生思考和讨论.

4.3 倡导自主学习

教师可以在学生已基本掌握“微元法”的基础上进一步提高要求.比如将一些现实原型划归为数学模型，尝试构造微元以及所求量的积分表达式.引导他们在寻求解答的过程中养成独立思考的习惯，懂得借助多媒体扩充知识面、寻找参考资料.

实践表明，经过上述教学过程，学生在不同程度上能做到微元法思想的拓展与创新，并能锻炼和提高数学建模的能力.

[1]邓东皋，尹小玲.数学分析简明教程[M].北京：高等教育出版社，2002.

[2]欧阳光中，姚允龙.数学分析[M].上海：复旦大学出版社，1993.

[3]华东师范大学数学系.数学分析[M].北京：高等教育出版社，2001.

(责任编辑 张建军)

2014-08-26

陈平，女，湖北荆州人，江苏第二师范学院数学与信息技术学院讲师，博士.

O172.2

A

1671-1696(2014)11-0024-03