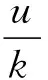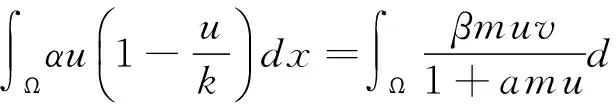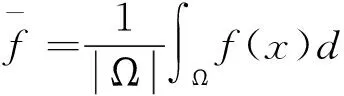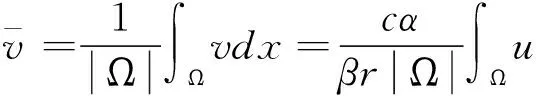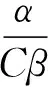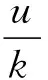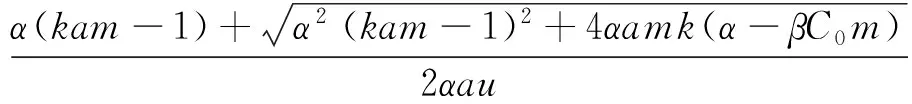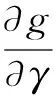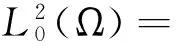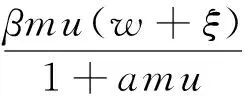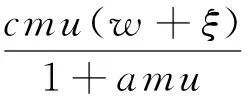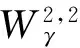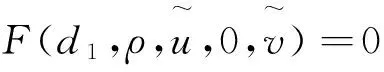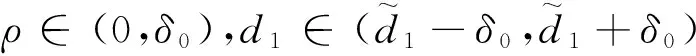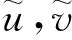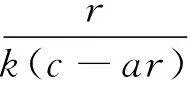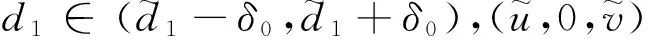一类具有Holling-II型响应函数的捕食模型非常数正解不存在性的进一步分析

王 鲁 欣

(南通航运职业技术学院基础部，江苏南通 226010)

一类具有Holling-II型响应函数的捕食模型非常数正解不存在性的进一步分析

王 鲁 欣

(南通航运职业技术学院基础部，江苏南通 226010)

本文进一步讨论了一类具有Holling-II型响应函数的捕食模型的齐次Neumann问题的非常数正解的不存在性.

捕食模型；非常数正解；隐函数定理

1 引言

具有Holling-II型响应函数的捕食模型对应的反应扩散方程组的齐次Neumann初边值问题是

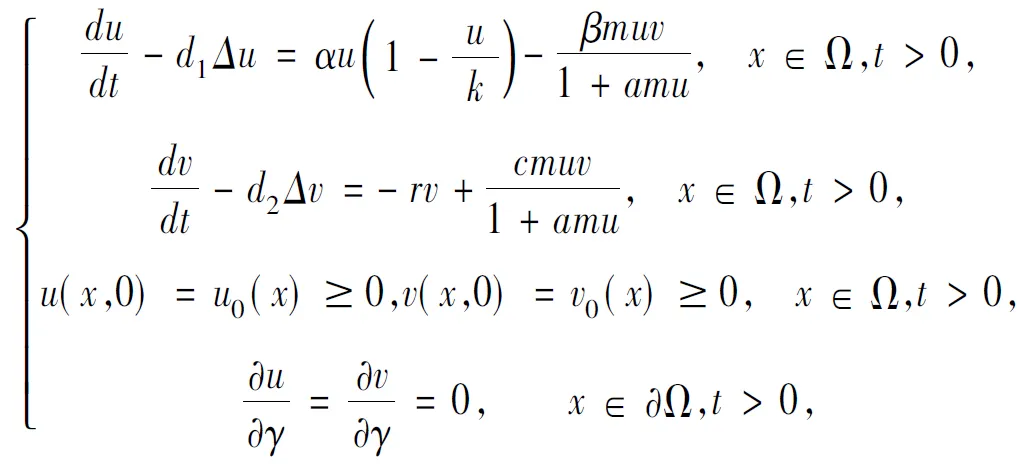
(1)

其中Ω是RN中的有界光滑区域，γ是∂Ω上的单位外法向量，di>0(i=1,2)表示扩散系数，α,k,r,β,a,c都为正常数，m∈(0,1]为常数，u0(x),v0(x)是连续函数.相应的平衡解方程为

(2)

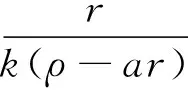
2 定理证明

定理1 若m0

(3)

同样对(2)中第二个方程两边积分，再利用边界条件可得

(4)

(5)

d1>ε时，(2)没有非常数正解.

下面主要利用隐函数定理来证明定理2，首先给出两个引理.

引理3 若f(u)为定义在[0,)上的一个连续实函数，对某个正常数a，有当u∈(0,a)时，

f(u)>0，当u∈(a,)时，f(u)<0，则问题-Δu=uf(u),x∈Ω，∂γu=0,x∈∂Ω

仅有唯一的常数正解a.

证明：应用极大值原理即可证明引理.

引理4 设d,a,α,β,c,r,k,m为固定的正常数，并且d1≥d,d2≥d，α>mβC，C为定理1估计出的(2)正解的上界，假设(ui,vi)为(2)的一个正解，其中d1=d1,i，d2=d2,i.若当i→时]，d2,i→，则当i→时).

证明：由d2,i→知vi→C0(常数)，假设ui→u.若，易得).若，则有1--,x∈Ω，

由条件α>mβC知α>mβC0，再由上面的引理可知

u=

混凝土路面平整作业结束之后需要对混凝土路面采取养护处理。本工程通过对混凝土喷洒养护剂进行养护。当混凝土强度达到规定要求时，采用4m长的直尺沿着路面板块的纵横向检测路面平整度。对混凝土路面养护28d后，为了能准确检测混凝土路面的强度、密实度等参数指标，需要对混凝土路面采取抽芯试验。检测应当及时实施，可得到准确参数指标，为后续优化工作提供指导。

f3(d1,ρ,u,w,ξ)=Δw+

F(d1,ρ,u,w,ξ)=(f1,f2,f3)(d1,ρ,u,w,ξ),

则

(6)

先证Ψ是一个单射.设Ψ(y,z,τ)=(0,0,0),因为

[1]王鲁欣，陈文彦.一类具有Holling-II型响应函数的捕食模型定性分析[J].东南大学学报(自然科学版)，2008(38).

[2]Peng R, Wang M X.Pattern formation in the Brusselator system[J].J.Math.Anal.Appl., 2005(309).

[3]Pang Y H, Wang M X.Qualitative analysis of a ratio-dependent predator-prey system with diffusion[J].Proc. R. Soc. Edinburgh A, 2003(133).

[4]Nirenberg L.Topics in Nonlinear Functional Analysis[M].New York: Courant Institute of Mathematical Science,1973.

(责任编辑 张建军)

2014-05-20

王鲁欣，女，江苏南通人，南通航运职业技术学院基础部讲师，硕士.

O175.26

A

1671-1696(2014)11-0001-03