关于分式线性变换的一点思考*

张 杰 康 海 燕 任 新 安

(中国矿业大学理学院数学系，江苏徐州 221116)

关于分式线性变换的一点思考*

张 杰 康 海 燕 任 新 安

(中国矿业大学理学院数学系，江苏徐州 221116)

分式线性变换是复变函数中最简单的一类解析函数，但却有着许多重要的性质.本文细化了一些已有的结论，还考虑了更广一些的解析函数，以及分式线性变换的其它一些新的性质.

分式线性变换； 解析函数；差分变换

1 分式线性变换简介

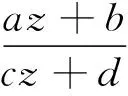
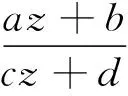
2 分式线性变换的类型

分式线性变换也是解析函数中最简单的一类函数，却具有很好的性质，起着很大的作用，可以作为解析函数研究的重要工具.我们知道每一个分式线性变换都可以分解为以下四种基本分式线性变换：

(1)旋转L(z)=eiθz,其中θ是实数；

(2)伸缩L(z)=rz,r>0；

(3)平移L(z)=z+a,其中a是实数；

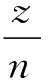
3 分式线性变换的性质

我们知道分式线性变换具有保圆、保角、保交比、保对称性等性质，即有下面的定理.

定理1[2，3]线性变换具有保圆周性.

我们对该定理作如下一些详细的说明，即上面四种基本分式线性变换具体保圆性质：

我们分以下两大类考虑：

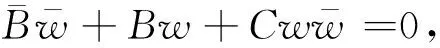
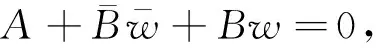
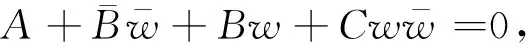
综上所述，我们可以得到如下结论：

例1 求将上半平面变为单位圆盘的所有分式线性变换.

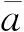
4 分式线性变换间的运算

4.1 分式线性变换间的差分运算

差分方程理论和求解方法在数学建模和解决实际问题的过程中起着重要作用.已知L(z)是分式线性变换，那么L(z+1)也是一个分式线性变换，它可以看成L和平移的复合，定义L(z+1)-L(z)为L的差分运算.对于线性变换与差分方程，我们容易有下面这个定理.

定理 2 设L(z)是分式线性变换，那么L的差分运算L(z+1)-L(z)不再是分式线性变换.

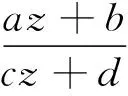
当c≠0时，L(z+1)-L(z)是一个2次有理函数.所以L(z+1)-L(z)不是分式线性变换.

4.2 分式线性变换间的乘积运算

显然，分式线性变换之间的乘积运算不再是分式线性变换，但有限个分式线性变换之间的乘积也有很好的性质和作用.

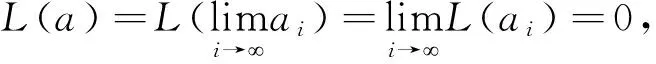
结论：对于分式线性变换L(z)，经过四种基本分式线性变换复合后是分式线性变换，但是仅限于复合运算，不能推广到四则运算(特别地，差分运算).

最后我们把保圆、保角定理结合起来作如下一些说明，分式线性变换把圆Γ1映射为圆Γ2，那么如何判别把圆的内部映射为圆的内部还是圆的外部.我们只要在Γ1上按照Γ1围的圆γ1的正向依次取3个点z1，z2，z3，即z1→z2→z3，保持区域γ1在左手边，然后找出它们的像w1，w2，w3，绕Γ2走时，左手边的区域就是γ1的像.

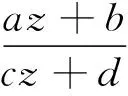
解：设L(z)是将边界R映射为边界R的分式线性变换，那么产生的结果就是：

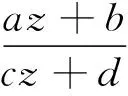
[1]Tristan N. Visual, Complex Analysis[M]. Oxford: Oxford University Press, 1997.

[2]谭小江，伍胜健.复变函数简明教程[M].北京：北京大学出版社，2006.

[3]廖良文.复分析基础[M].北京：科学出版社，2014.

(责任编辑 张建军)

] 校级项目“关于《复变函数》课程教学改革的一些研究”(项目编号：2014QN34).

2014-8-23

张 杰，男，江苏常州人，中国矿业大学理学院讲师，博士.

0174.5

A

1671-1696(2014)11-0004-03

* [