极紫外多层膜反射率的模拟计算与分析

易子为， 曾 涛， 孙 翔， 程发银

(重庆工商大学 计算机科学与信息工程学院，重庆 400067)

由于衍射，所有光学器件都存在一个分辨率极限，这个极限与使用的光波波长相关.为了提高光学器件的分辨率，最有效和直接的方法就是使用波长更短的光波.然而，当把使用的光波由可见光延伸到极紫外和软X射线波段(波长0.3～40 nm，通常将5～40 nm波段称为极紫外线)时，遇到了前所未有的困难，以至于这一波段电磁波在光学器件中的应用出现了很长一段时间的停滞.主要的原因是，在该波段内存在大量的原子共振线，使几乎所有材料对该波段电磁波均有强的吸收，吸收长度仅为纳米的量级.这使得在极紫外和软X射线波段的透射式光学器件的应用受到了极大的限制.

为了提高非掠入射条件下的反射率，可以类比可见光波段使用多层镀膜提高反射率的方法，将具有高低原子序数的两种材料交替沉积在基底材料表面，当每层厚度约为λ/4时，可使反射光在界面上相长干涉而加强，从而提高反射率.通过这种思路制作多层膜的尝试虽然很早就展开了[5]，但由于加工和制备技术的限制，这些尝试都没能成功.20世纪70年代后，天体物理、等离子体物理以及同步辐射技术的飞速发展迫切要求研制极紫外和软X射线波段非掠入射光学元件，同时，纳米级薄膜技术的发展也为该波段多层膜的制备提供了技术条件.1972年，E.Spiller[6]首先提出用非吸收 (散射)材料和吸收材料交替制备λ/4波堆，理论表明这种多层膜结构可以获得较高的非掠入射反射率.目前，世界上已有多家研究小组能制备出性能优良的极紫外和软X射线正入射多层膜，如美国Lawrence-Livermore实验室在11.3nm处采用Mo/Be材料对，制备的多层膜正入射反射率达到了70.2%[7].而基于多层膜的反射式光学器件已在极紫外投影光刻、生物学、生命科学与医学、天体物理学、X射线激光和同步辐射及等离子体物理等领域得到了广泛的应用.

此处建立理想化界面条件下的极紫外多层膜模型，使用matlab软件编程，计算和分析了Mo/Si多层膜的反射率随入射波长的变化，获得了高反射率波段的中心波长，在中心波长下，计算了反射率随膜层数及入射角等的变化曲线.

1 复折射率和光学常数

电磁波与物质相互作用的许多现象，包括折射、散射以及近掠入射时的全反射等都可以基于束缚电子的散射来解释.

对于原子序数为Z的散射体，可用相对论量子色散理论[8]计算原子散射因子：

f(E)=f1(E)+if2(E)

(1)

(2)

(3)

式(3)中，σ(E)是原子光电吸收截面，可由质量吸收系数ηm算出：

σ(E)=Aηm/NA

(4)

式(2)右边第一项描述的是Thomson散射.为了描述散射与角度的关系，这一项可由与角度有关的因子f0来代替：

(5)

这里，U(r)是电荷的径向分布，式(2)第二项是反常色散积分，第三项是相对论修正项.

(6)

(7)

这里，na是材料原子数密度，re=2.82×10-13cm是经典电子半径.

从以上各式可见，知道了材料的散射因子，就可以计算出材料在不同光子能量E下的复折射率.B.L.Henke[9，10]等已给出了不同原子的散射因子的数值，此处通过对数差值，得到了钼和硅在极紫外相关波段的散射因子数值，并根据式(6)和式(7)获得了两种材料的复折射率.图1和图2分别给出了钼/硅的光学常数α和β随波长的变化曲线.可以看出，钼和硅的光学常数α和β在极紫外波段都是一个小量.

图1 光学常数α随波长λ的变化曲线

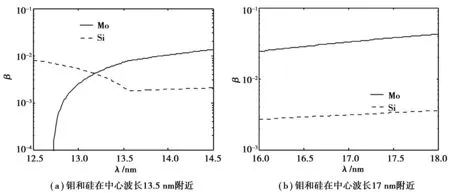
图2 光学常数β随波长λ的变化曲线

2 多层膜反射率的计算模型

(8)

式(8)中，Rj和Rj-1分别是镀完第j层和j-1层时，膜系的总复振幅反射率；rj为第j层材料对真空的Fresnel反射系数，δj为相位差，它们分别表示为

(s偏振)

(9)

(10)

(11)

3 Mo/Si多层膜反射率的模拟计算

用Matlab软件编程计算了钼/硅多层膜的反射率.首先，在中心波长13.5nm和17.1nm处对膜系的最佳膜层数进行了优化.为了提高反射率，通常采用多层镀膜的方法，但反射率不会随膜层数增加而无限制地趋于100%，因为材料的吸收，当膜层数增加到一定程度时，反射率达到饱和，之后增加膜层数反而会使反射率降低.图3显示了中心波长为13.5nm和17.1nm时，正入射反射率随膜层数的变化.其中，13.5nm波长取周期膜厚6.8nm，而17.1nm波长取9.0nm.结果显示，对13.5nm和17.1nm波长，最佳膜层数分别为80层和60层.

图3 正入射时反射率随膜层数的变化

其次，对反射率最大的波长数值进行了优化.图4显示了在波长为13.5nm和17nm附近反射率随波长的变化曲线，其中13.5nm波长附近取周期膜厚为6.8nm，正入射，膜层数N=80；17nm附近取周期膜厚9.0nm，正入射，膜层数N=60.结果显示，在波长为13.3nm和17.2nm处出现反射率峰值，反射率分别达到73.1%和53.7%.

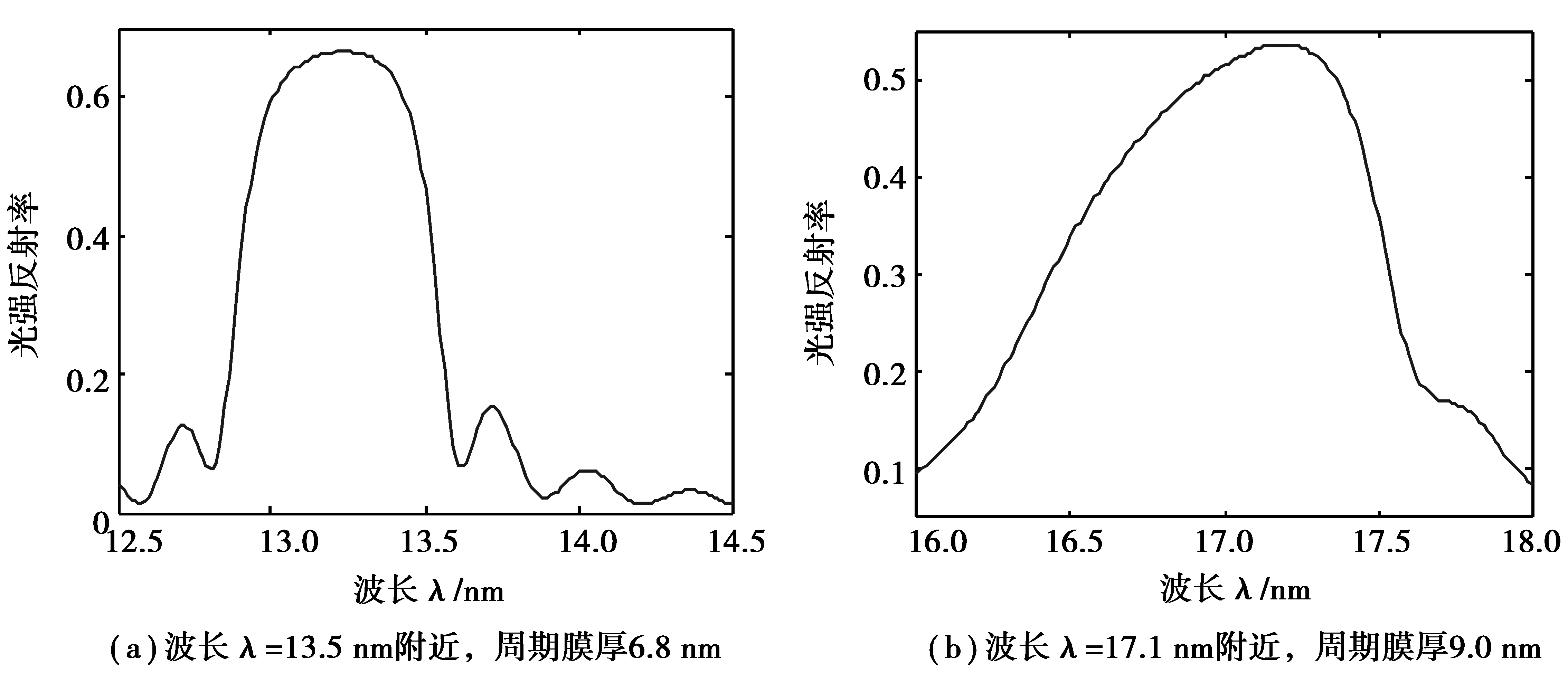
图4 正入射时反射率随波长的变化

最后，对反射率随入射角的变化作了计算(图5).可以看出，对13.3nm和17.2nm两个波段，在入射角小于8°的近正入射情形均存在一个反射率曲线平坦段.随入射角增大，反射率快速降低，虽然在某些角度处会出现一些布拉格峰值，但总体反射率维持在较低水平.

4 结论和分析

通过编程计算可见，对钼/硅多层膜，在极紫外波段的13.3 nm和17.2 nm处可得到较高的峰值反射率，尤其对13.3 nm波长峰值反射率可达到73.1%；但是高反射率仅在入射角小于8°的近正入射情形出现.此处的计算结果是在理想膜层界面条件下得到的，实际多层膜由于镀膜工艺条件的限制，以及界面间原子的相互扩散，会使反射率降低[5].尽管如此，计算结果仍然对多层膜的加工和实际应用具有一定的指导意义.

参考文献：

[1] 王占山， 吴永刚， 陈玲燕. 极紫外和软X射线光学[J]. 同济大学学报，2002，30(4)：510-515

[2] 张俊平，曹建林，马月英. 软X光激光用多层膜反射镜的设计与性能模拟计算[J]. 光学学报，1995，15(8)：1088-1093

[3] KIRKPATRICK P, BAEZ A V. Formations of Optical Images by X-ray [J]. J Opt Soc Amer，1948(38)：766-774

[4] 张立超. 极紫外多层膜技术研究进展[J]. 中国光学与应用光学，2010(6)：554-565

[5] DUMOND J, YOUTZ J P. An X-ray Method for Determining Rate of Diffusion in Solid State[J]. J APPl Phys，1940，11(5)：357-365

[6] SPILLER E. Low-loss Reflection Coatings Using Absorbing Materials[J]. Appl Phys Lett，1972，20(9)：365-369

[7] SKULINA K M，ALFORD C S，BIONTA R M，et al. Molybdenum/Beryllium Multilayer Mirrors for Normal Incidence in the Extreme Ultraviolet[J]. Appl opt, 1995，34(19)：3727-3731

[8] JAMES R W. The Optical Principles of The Diffraction of X-Rays[M].New York：Cornell University Press，1982

[9] HENKE B L，LEE P，TANAKA T J，et al. Low-energy X-ray Interaction Coefficients，Photoabsorption，Scattering，and Reflection E=100～2 000eV，Z=1-94[J]. At Data Nucl Data Tables，1982(27)：1-144

[10] HENKE B L，GULLIKSON E M,DAVIS J C. X-ray Interactions：Photoabsorption，Scattering，Transmission，and Reflection at E=50-30000eV，Z=1-92[J]. At Data Nucl Data Tables，1993(54)：181-342

[11] BERNING. Theory and Calculations of Optical Fhin Films，in Physics of Thin Films[M]. New York：G Hassed，Academic Press，1963