巴特沃斯低通滤波器优化设计与仿真研究*
2014-08-08林开司林开武
林开司, 张 露, 林开武
(1.铜陵职业技术学院 电气工程系,安徽 铜陵 244000;2.铜陵有色股份铜冠信息科技有限责任公司,安徽 铜陵 244000)
巴特沃斯低通滤波器由于其通频带内响应平坦,衰减特性和相位特性好,对构成滤波器的器件的要求不甚严格,易于得到符合设计值的特性,适应性强等特点而受到广泛使用[1]。
有关压控电压源巴特沃斯低通滤波器的设计在许多文章中都有介绍,主要方法有查表法[1]、图示法[2]、计算法[3,4]等,但这些方法都存在一些不足,不能满足普遍的要求;有些设计是先确定电阻,再匹配电容,但特定电容难找,订制时间长、成本高,且电容精度也较电阻难以保证;一些查表法、图示法和一些计算法没有给出必要的理论根据和计算通式,使用者难以明白其取值的根据[3,4]。
文献[6]对二阶压控电压源低通滤波器进行了比较详细的理论推导,文献[5]在文献[6]的基础上以四阶压控电压源单位增益巴特沃斯低通滤波器为例,介绍了2n阶压控电压源低通滤波器的设计。在文献[5,6]的基础上优化设计了六阶单位增益巴特沃斯低通滤波器,并且通过Multisim10[7]仿真研究了电路中电容间容值的不同比值k以及电路中电容值的变化对设计的低通滤波器幅频特性的影响。
1 二阶压控电压源低通滤波器设计
六阶低通滤波器可以有3个二阶低通滤波器级联产生,所以先根据文献[5,6]介绍二阶低通滤波器的优化设计方法。常用的二阶压控电压源低通滤波电路如图1所示。
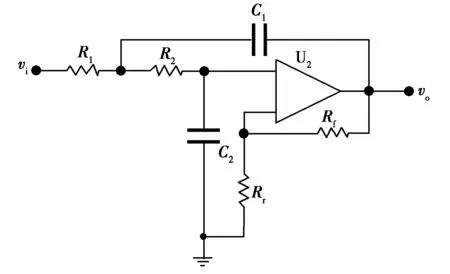
图1 二阶压控电压源低通滤波电路
由图1可知其传输函数为
(1)
(2)
两式比较得
(3)
(4)
(5)
ω0是截止角频率,α,β是二项式系数,代表不同的滤波特性。令
C2=kC1
(6)
由式(3)(4)(5)(6)得
(7)
式(7)是关于R2的二次方程,因为R2有实数解,所以k必须满足
(8)
由式(7)可解得
(9)
同理解得
(10)
所以原则上选定C1,k后根据上述计算公式设计任意特性的压控电压源低通滤波器。
2 六阶单位增益压控电压源低通滤波器的设计

设计实例:设计六阶压控电压源单位增益巴特沃斯低通滤波器,截止频率为100 kHz,增益G=1。电路仿真图如图2所示。

图2 仿真电路
六阶滤波器的α值分别为0.517 6,1.414 0和1.931 8,根据最简单取值情况计算出的各电阻、电容值如图2所示。仿真得到该滤波器的幅频特性曲线如图3所示。
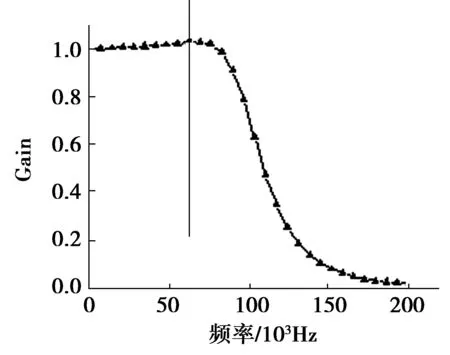
图3 幅频特性曲线
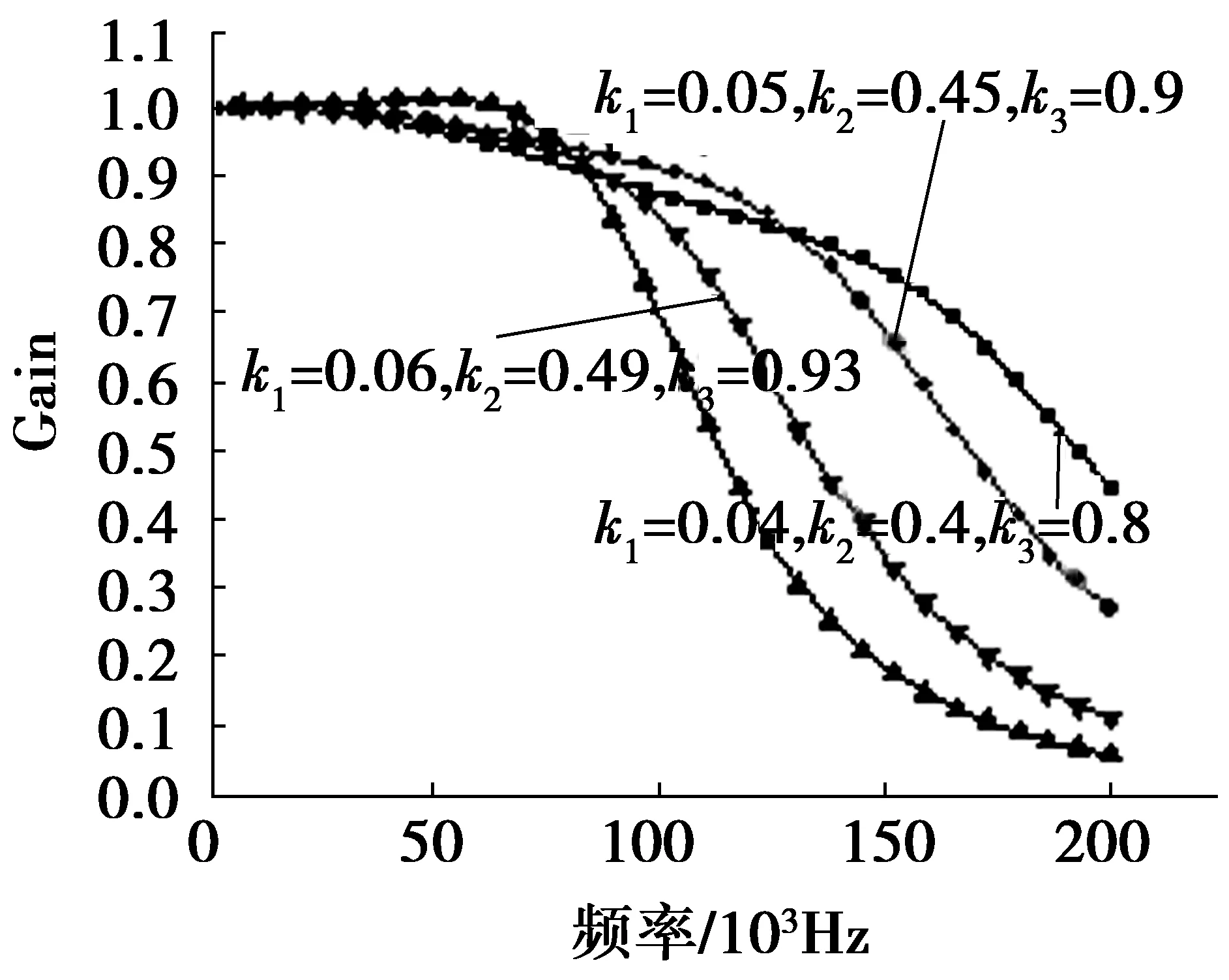
图4 不同k值对应的幅频特性曲线
由图3幅频特性曲线可看出,这种方式设计的六阶单位增益巴尔沃斯低通滤波器具有较理想的幅频特性。
3 取不同k值对幅频特性的影响
上面的取值方法最简单,且使得R3=R1+R2,R7=R5+R6,R10=R9+R12,这也使元件规格减少一种,订货和装配都较方便,成本也可降低。但是否是最好的取值还需进一步仿真研究。取不同的k值对应其他的电阻电容取值如表1所示。为了便于说明把六阶滤波器分成第一级二阶滤波器、第二级二阶滤波器和第三级二阶滤波器,对应的k值分别为k1,k2和k3。另外三级的k值均按照同时减小的方向取值。

表1 不同k时电路中其他电阻电容的取值
由上面分析可知图2中R1=R2,R5=R6,R9=R12,C2=C4=C6=2.2nF。R3=R1+R2,R7=R5+R6,R10=R9+R12,而R4,R8,R11取1 T的大值电阻,因此所有的元件值都已经确定。针对不同的k值仿真得到的幅频特性曲线如图4所示。
由图4看出按照最简单的方式,即优化方法设计的各元件的参数值具有最优的幅频特性曲线,另外随着三级对应的k值同时越减小得到的幅频特性越差。
4 元件数值变化对幅频特性的影响
为了突出电路中元件参数的变化对优化设计出的低通滤波器的幅频特性的影响,考察电路中各电容按+20%和-20%变化的情况。另外通过Multisim10仿真发现电路中电阻的较小变化对幅频特性曲线的影响较小,所以省略仿真图,且只说明电容变化的情况,如图5、图6所示。

图5 电容值加20%

图6 电容值间20%
由图5和图6可知电容C2,C3,C5电容值变化对低通滤波器的幅频特性的影响较大,另外C6在电容值减小时对滤波器幅频特性的影响也较大,除此之外其他电容值的改变对滤波器的幅频特性影响较小。所以在实际使用中应尽量减小C2,C3,C5,C6电容值的变化,使用精度相对较高的电容,其他情况电容可以容忍较大电容值的变化。
5 结束语
对巴特沃斯低通滤波器的优化设计进行了理论分析,并设计了一个六阶单位增益巴特沃斯低通滤波器,通过Multisim10对设计的滤波器进行仿真,研究了k值的变化对滤波器幅频特性的影响,另外还仿真研究了电容值变化对低通滤波器幅频特性的影响。方法对实际低通滤波器的设计具有一定的参考价值。
参考文献:
[1] 张白莉,郭红英. 基EWB的巴特沃斯有源低通滤波器的设计与仿真[J]. 吉林师范大学学报:自然科学版,2011,(4):77-79
[2] JL希尔本,DE约翰逊. 有源滤波器设计手册[M] . 北京:地质出版社,1980
[3] 秦世才,王朝英. 集成运算放大器应用原理[M].天津:天津科学技术出版社,1983
[4] CARTER B,MANCINI R. OpAmps For Everyone(3E) [M]. Singapore:Elsevier (Singapore) Pte Ltd,2009
[5] 杨勇,邢磊,诸远奇,等. 压控电压源2n阶单位增益巴特沃斯低通滤波器优化设计[J]. 电子学报,2011,39(8):1894-1897
[6] 高明甫,杨勇,孔令斌. 二阶压控电压源低通滤波器设计[J]. 电子技术,2010(3):73-75
[7] 郭锁利. 基于Multisim的电子系统设计、仿真与综合应用[M]. 北京:人民邮电出版社,2012
